多中心社区居家养老服务调度与服务网络优化
丁 锋,付亚平,王 伟,王洪峰
(1.青岛大学商学院,山东 青岛 266071;2.东北大学信息科学与工程学院,沈阳 110819)
0 引言
中国人口老龄化形势日趋严峻。根据预测,中国将于2035年前后步入“深度老龄化”社会,届时65岁及以上老年人口比重将超过21%[1],而应对老龄化的关键在于能否显著改善和维护老年群体的健康[2]。社区居家养老服务作为一种新颖的养老模式,在解决中国老有所养的问题上发挥着重要作用。在社区居家养老日常服务中,社区医疗中心通常要解决为护工分配老人及规划服务路径的问题,即社区居家养老调度与服务网络优化问题。这类问题属于NP问题[3]。合理地调度服务人员,优化服务次序与路线,对于充分利用人力和医疗资源、提升客户满意度和提高服务质量等都具有重要的意义。
居家养老问题从20世纪90年代就开始受到学者的关注,但国内针对此类问题的研究较少。袁彪等[3]以家庭医疗护理(Home Health Care,HHC)中的人员调度为研究对象,建立数学模型并设计出有效算法来解决所提问题。杨欣湩等[4]研究的中国居家养老问题,通过改进算法大幅减少了时间成本。此外,国外学者在HHC领域的学术成果较多。许多研究在随机环境中定义问题[5-6];此外,一些研究对护工的医疗资格作出分类[7-8];还有部分文章考虑了客户时间窗[9-11]。以上文献大多只考虑一个医疗中心,但少数涉及多医疗中心问题特点[5,12]的研究则更加符合现实情况。
实际上社区居家养老调度与服务网络优化问题与带时间窗的车辆路径规划问题(Vehicle Routing Problem with Time Windows,VRPTW)在车辆调度和路网规划方面具有相似性[13-14]。但本文提出的社区居家养老问题同时考虑了随机环境、多医疗中心、预约服务时间和技能匹配等问题特点,与VRPTW仍有很大区别。文献中为解决HHC问题提出了许多方法,分为3类:1)精确式算法[5];2)启发式[11]或元启发式[9-10,12,15-16]方法;3)数学规划方法[17]。本文为了提高老人的满意度,还引入等待时间的机会约束,建立了一个带机会约束的随机期望规划模型,并设计了改进混合牧羊人优化算法(Shuffled Shepherd Optimization Algorithm,SSOA)[18-19]求解此复杂但具现实意义的社区居家养老调度与服务网络优化问题。
1 问题描述及数学模型
1.1 问题描述
社区居家养老日常调度和服务网络优化问题可以描述如下:某社区有H个医疗中心(集合为I)共同为C位老人提供服务(集合为J),构成一个有向网络节点集G={N,φ},其中N=I∪J是点集,φ={(i,j)|i,j∈N,i≠j}是弧集,经过弧(i,j)∈φ的时间为tij。每位老人i∈J有护理需求ri(等级集合S={1,2,…,L}),服务时间τi和预约时间Ai。各医疗中心h∈I有Kh名护工参与服务(集合为Vh,护士总集合V={V1,V2,…,VH}),每名护工k∈V有护理水平qlk,(l∈S)和服务人数限制Q。
根据问题描述,对模型进行假设:1)各中心服务人数固定;2)护工从所属中心出发,并最终回到该中心;3)每名护工的服务人数不超过Q;4)护工技能水平须与老人需求匹配,技能水平须大于等于需求等级;5)每位老人仅可被一名护工服务;6)老人接受服务时长与护工技能水平相关。
1.2 数学模型
基于以上,引入以下常量、变量、参数及数学模型。
M:一个很大的常数;Aj:老人j的预约开始服务时间;chl:中心h负责服务需求等级为l的老人数量;zjk:护工k服务第j个老人的到达时间;K:所有中心参与服务的护工总数;sjk:护工k服务第j个老人的开始时间;tij:护工从节点i前往节点j所需旅行时间;D:预设延迟到达目标老人的允许时间上限;τjk:老人j接受护工k服务所需的服务时长;φ:护工到达延迟时间不大于D的置信度。
决策变量:
其中,tij和τjk是服从截断正态分布的随机参数。老人j接受护工k服务的时间τjk可用公式(1)计算:
(1)
护工在老人i与j间的辗转和服务时间不确定,使护工到达时间zjk无法预估。可用公式(2)表示:
(2)
若护工k早于老人i的预约时间到达,需等待至Ai开启服务。护工空闲时间可按公式(3)计算:
(Ai-zik)+=max{(Ai-zik),0}
(3)
数学模型为
(4)
s.t.
(5)
(6)
|cil-cjl| (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) τjk≥0,j∈J,k∈V (17) xijk∈{0,1},yik∈{0,1},i,j∈N,k∈V (18) 上述模型中,式(4)为期望目标函数;式(5)表示护工服务人数限制;式(6)表示各中心协同服务;式(7)保证分配合理性;式(8)表示护工总数;式(9)表示各中心有多条访问回路;式(10)保证每位老人仅由1名护工服务;式(11)表示护工可服务多位老人;式(12)表示每名护工只属于一个中心;式(13)表示技能约束;式(14)保证各中心的访问路径不超过其护工数;式(15)表示老人的开始服务时间;式(16)保证老人的总等待时间小于给定值的概率大于或等于给定置信度;式(17)表示非负约束;式(18)表示决策变量为0-1变量。 现有居家医疗护理研究中,多采用元启发式方法进行求解,如基于种群的遗传算法(Genetic Algorithm,GA)[10,12]、粒子群算法(Particle Swarm Optimization,PSO)[12,16]等。Kaveh和Zaerreza[18]提出一种先分割后合并、基于种群的优化算法,称为混合牧羊人优化算法,本文也将基于该算法对问题进行求解。 SSOA首先会随机生成一个种群,候选解视为羊。其次,将羊按其目标值升序排列(最小化问题),选出前m(牧群数量)只羊,分别随机放入一个牧群,重复执行,直到分配完毕。接着,按公式(19)和(20)为每个牧羊人计算步长及临时位置: Stepsizei=α×rand∘(Xj-Xi)+β×rand∘(Xd-Xi) (19) (20) 其中,Xi,Xd,Xj分别为牧羊人、马以及羊的个体解;rand是随机向量,所有分量都是[0,1]上的随机数;α=α0(初始参数),可用公式(21)更新;β=β0(初始参数),可用公式(22)更新;符号“∘”表示向量的逐元素乘法。如果牧羊人的新位置不比之前差,则更新为当前位置(替换策略),所有牧群都会重复执行此过程。最后,将所有牧群重新合并为种群。重复上述过程,直到满足停止条件。 (21) (22) 本文提出的社区居家养老问题是典型的离散优化问题。公式(19)是牧羊人步长计算公式。第一项α×rand∘(Xj-Xi)表示牧羊人走向羊;第二项β×rand∘(Xd-Xi)表示牧羊人驱赶羊走向马。改进SSOA的关键在于根据离散问题特点重新定义步长公式。设计的改进将α×rand∘(Xj-Xi)视为当前解与差解的概率交叉,α为交叉率;将β×rand∘(Xd-Xi)视为当前解和优解的概率交叉,β为交叉率。 改进后的算法具体步骤如下。 步骤1确定编码机制,生成初始种群。对于有H个中心,C位老人的HHC问题,编码方式如下:首先按约束(7)确定各中心的老人;接着,各中心按约束(5)和(13)确定护工类型和数量,共有K人;然后,各中心再将老人分给合适的护工;最后,护工按预约访问。将老人编号为1~C,中心编号为1~H,护工根据其所属的中心和技能水平编号,例如第1中心的技能水平为3的护工可以表示为“1003”。 步骤2计算种群中个体的适应度值。取M1次试验结果的平均值作为评价依据。在此基础上,根据机会约束(16),得M1次试验中共有M2次未超出老人等待时间上限D。若(M2/M1)<φ,则该解不满足机会约束,即为不可行解,需对其进行惩罚,令其适应度值乘上惩罚系数ε,并以此作为其新适应度值。 步骤3分离种群,构建牧群。根据个体适应值,对种群从小到大(最小化问题)排列,选择前m头羊放入多牧群向量集第一列,作为每个牧群的第一头羊,并且每一行都表示一个牧群。重复以上过程n次(牧群大小n,种群大小N=m×n),直至牧群构建完成。 步骤4交叉算子,更新种群位置。根据步长公式(19)的新定义,将牧羊人(当前解)先后与其对应的羊(较差解)、马(较好解)进行概率交叉,交叉方式采用改进的部分匹配交叉(Partial Mapped Crossover,PMX)。如图1所示,对参与交叉的两个个体,首先随机选中相同位置的两条子路径并构造映射关系:对有相同需求的节点构建映射,且相同节点优先对应;然后整体交换两条选中子路径的节点;最后,对交换后的个体做冲突检验,并根据映射关系替换旧路径中的重复节点。经过与羊、马的交叉,可以得到牧羊人的临时位置,若不差于之前位置,则接受新位置。重复此过程,完成种群位置的更新。 图1 交叉算子 步骤5更新参数。依据公式(21)和(22)对参数α,β进行更新。 步骤6判断是否满足停止条件。若未满足停止条件,则转步骤2;否则,算法停止搜索。 在本节中,首先生成问题的测试算例;然后为算法设置参数,并进行算例试验;最后,通过比较、分析实验结果,验证算法的有效性。本文所有程序均通过C++实现,运行于Visual Studio 2017。 本文以Homberger[20]所提的VRPTW算例为基础,重构适合所研究问题的算例,包含C,R和RC 3种类型。其中,C表示老人集中分布,R表示随机分布,RC表示半集中混合分布。修改后的算例有如下特点:1)标准服务时间τj服从均值为90的截断正态分布,标准差是均值的0.001倍;2)时间窗左端作为预约时间;3)5种服务需求比率为Rs={0.2,0.15,0.3,0.15,0.2};4)旅行时间服从截断正态分布,均值以两点欧氏距离表示,标准差是均值的0.001倍。基于以上修改,对采用的VRPTW标准算例分别选取前50、100、150和200个节点作为老人坐标,并构造包括小、中、大3种规模在内的12组测试算例。 本文设置牧羊人和马的最大交叉率βmax=1。此外,SSOA的种群规模N、牧群规模n、牧羊人与羊的初始交叉率α0以及牧羊人与马的初始交叉率β0的设置需通过正交实验完成。各参数均设置4个水平:N={30,60,60,90},n={3,6,10,15},α0={0.1,0.3,0.5,0.7},β0={0.2,0.4,0.6,0.8}。表1是规模为L16(44)的正交表,实验基于100规模的C类算例,当总估值次数达到3 600次时停止搜索。对每组参数组合都独立运行20次,并计算平均值作为平均响应值(Average Response Value,ARV)。表2列出了每个参数的ARV。由表1和表2实验结果可得一组效果较好的SSOA参数设置:N=30,n=10,α0=0.5,β0=0.8。 表1 正交表和实验结果 表2 各参数不同水平下的平均响应值和影响力 在求解HHC问题方面,GA和PSO分别作为进化算法和群体智能优化算法的代表,已经得到了广泛应用[10,12,16],且效果显著。因此,本文选择GA和PSO作为对比算法。 根据文献[12]设置PSO参数:粒子数P=75,惯性权重w=0.54,学习因子c1=0.7,c2=1.42;设置GA参数:种群Npop=76,交叉率pc=0.5,变异率pm=0.27。每个算法的试验都独立运行20次,并以总估值次数150C作为停止条件。试验结果如表3所示,Gap%是对比算法与SSOA结果均值的相对偏差。此外,还通过95%置信度下的t检验方法,分析了试验结果的差异性。符号“+”、“-”分别表示SSOA结果显著优于或劣于对比算法,符号“~”代表SSOA与对比算法的结果无显著差异。 表3 3种算法运行结果对比 从表3可以看出,在50和100规模的试验中,SSOA绝对优于对比算法;随着规模扩大到150和200,结果差距略有缩小。进一步分析均值的相对偏差,PSO和SSOA的偏差在大规模算例中明显增大,最高偏差达20%;而SSOA与GA的偏差则保持在3%以内。通过以上分析,SSOA明显优于PSO,略优于GA,且比GA有更好的适应性。表3还展示了试验中达到的最小值。分析发现,SSOA在多数算例中达到最小值,反映出SSOA良好的全局搜索能力。分析t检验结果,SSOA显著优于PSO;且SSOA在75%的试验中,显著优于GA。t检验结果表明SSOA不仅拥有高效的搜索性能,还兼具卓越的搜索稳定性。 图2表示SSOA和对比算法进行20次试验后的箱线图。分析发现,SSOA在80%的算例结果中拥有最小的中位数,体现出SSOA稳定的搜索性能。在图2a、2b中,SSOA的测试结果比对比算法更加集中;在图2c、2d中,SSOA在所有大规模算例中有着更好的测试结果分布,如正态分布和左偏分布,都表明SSOA不仅能够应对中小规模问题,而且在解决大规模问题时同样出色。综上分析,改进SSOA在求解所研究的多中心社区居家养老问题方面效果显著,其搜索到的解优质且稳定。 图2 3种算法求解12个算例的箱线图 中国人口老龄化和医疗资源不平衡等问题加剧了社区居家养老需求。本文研究了随机环境下的多中心社区居家养老调度与服务网络优化问题,建立了带机会约束的随机规划模型。根据问题特点,设计了整体编码方法进行老人分配和路径规划。所提的改进SSOA,通过引入交叉算子,赋予原步长公式新解释,使步长更新仍然基于当前和其他个体的位置信息,使其可用于解决本文所研究的具有离散特点的社区居家养老问题。最后,测试了最大规模为200的一系列算例,结果表明改进SSOA在绝大多数情况中都能得到优于对比算法的结果,验证了所提算法的有效性。在此研究基础上,后续工作可以在考虑同步服务和选址-路径问题等方面作出扩展;还将继续改进算法,使其在解决大规模问题时更加高效和稳定。2 算法设计
2.1 基本的SSOA
2.2 改进策略
2.3 改进SSOA的框架
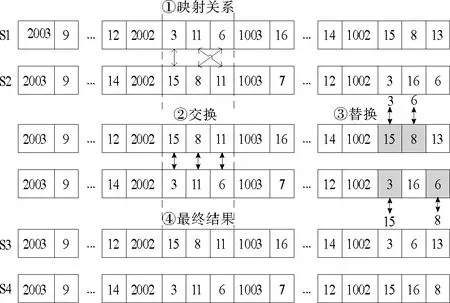
3 算例分析
3.1 算例生成
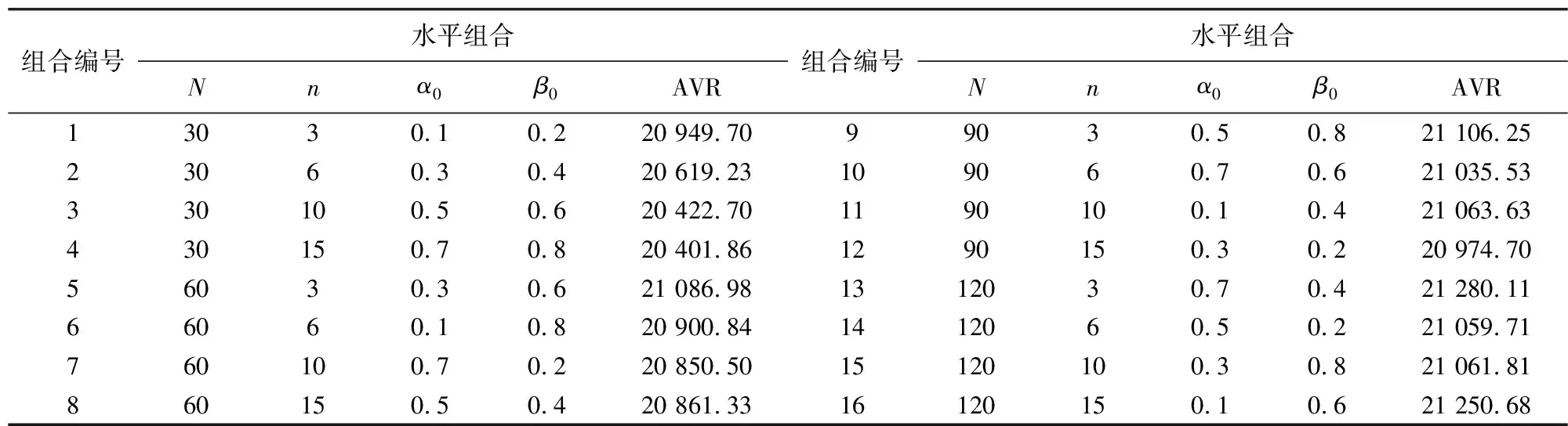
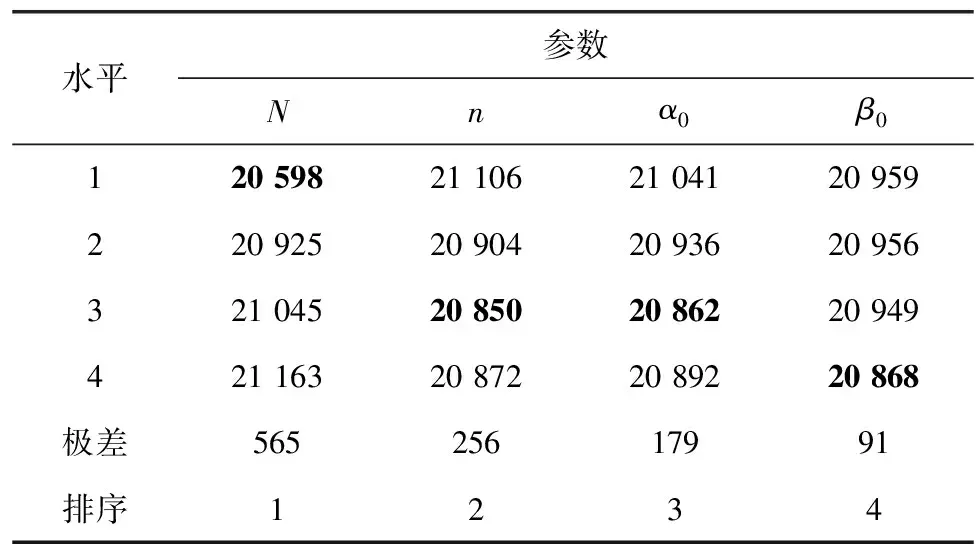
3.2 参数设置
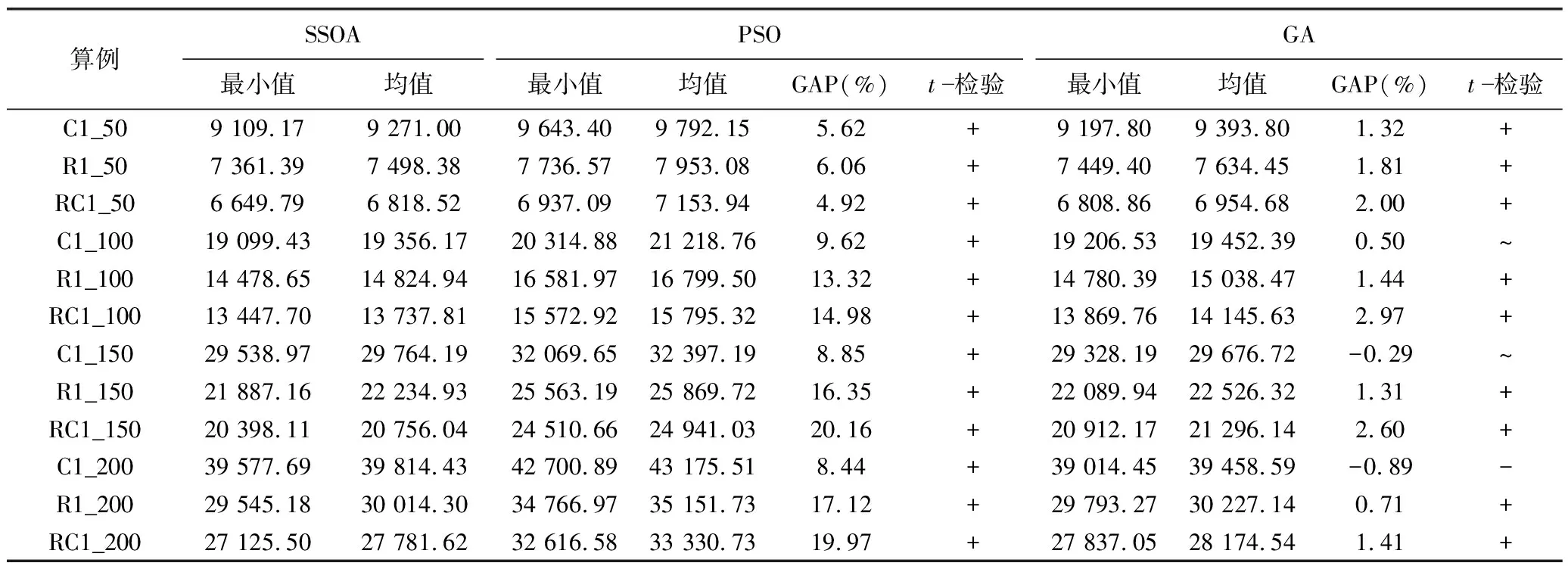
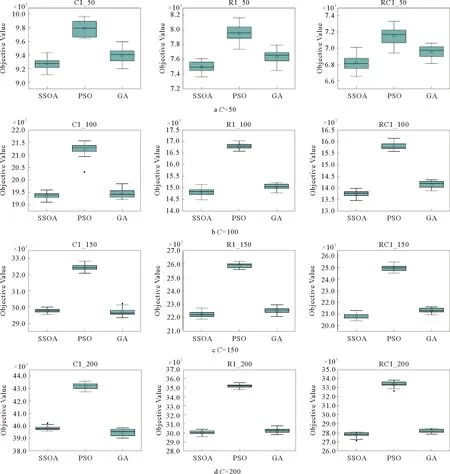
3.3 算法比较
4 结论

