多路径选择变速双目标物流配送路径规划
孔 珊,仲昭林,张纪会
(青岛大学 a.复杂性科学研究所;b.山东省工业控制技术重点实验室,山东 青岛 266071)
0 引言
车辆路径问题(VRP)是物流领域的热门课题。自Dantzig和Ramser[1]首次提出以来,一直备受关注。根据实际环境的不同,产生了多种变型问题,如绿色车辆路径问题、带有时间窗的车辆路径问题、多车型车辆路径问题、动态车辆路径问题、半开放式车辆路径问题、变速车辆路径问题等。多数模型都假设两点之间只有一条路径,且车辆匀速行驶,然而在实际路网中,任意两点之间可能存在多条道路,且同一路段上车辆在不同时间段内的行驶速度会有较大差异(比如城市交通高峰期和非高峰期情况)。另一方面,随着社会的发展,物流服务企业面临的竞争不断加剧,以时间窗刻画服务水平的传统方式具有一定局限性,需要根据客户的特点将客户分为不同类别(即考虑客户优先级)来提供不同服务。因此,研究路网中任意两点之间存在多条路径的带时间窗和能力约束的变速车辆路径问题具有重要意义。
对于变速车辆路径问题,Malandraki和Daskin[2]于1992年提出了用分段函数刻画旅行时间的混合整数线性规划模型。周鲜成等[3]研究时间依赖型绿色车辆路径问题时考虑了车辆出发时刻对行驶速度和行驶时间的影响,并采用改进蚁群算法求解。Poonthalir和Nadarajan[4]研究了高效绿色车辆路径问题,讨论了行驶速度对路线成本和燃料消耗的影响。Fan等[5]研究了时变多车场带时间窗绿色车辆路径问题,利用多个三角函数关系表示不断变化的车速,使其更加适合于动态环境。Gmira等[6]考虑路网中每个路段旅行时间的变化,采用禁忌搜索算法求解带有时间窗的车辆路径问题。
对于带有路径选择的车辆路径问题,Behnke和Kirschstein[7]的研究发现当两点之间存在多条路径时,通过合理的路径选择可以实现节能减排。Wang等[8]以节能和出行距离最小为目标建立多路径电动汽车物流线路规划模型。李顺勇等[9]考虑了城市交通拥堵造成的环境污染问题,研究表明优化路径选择能够明显降低配送车辆的油耗。程兴群等[10]对运输时间和单位运费率的概率分布未知情形下的多路径选择问题进行研究,建立鲁棒优化模型并设计了相应的算法。Sun等[11]综合多种因素,比较车辆路径选择对车辆的运行时间和乘客的出行时间的影响。Croce等[12]研究了道路交通中影响车辆路径选择的行为,结果表明行驶距离、行驶时间以及行驶成本(如能耗)等因素都会影响车辆路径选择。
在顾客满意度度量方面,余建军等[13]考虑生鲜外卖配送的送达时间对顾客满意度的影响,以配送成本最小和顾客满意度最大为目标,用改进的遗传算法求解。Barkaoui等[14]使用改进的混合遗传算法对动态环境下多次访问同一客户的DVRPTW问题的客户满意度进行详细研究,给出了新颖的满意度评价函数,通过多次服务客户的方式提高满意度。Rajak等[15]针对单一仓库不足以满足顾客需求导致顾客满意度下降的问题,提出了基于客户满意度的多仓库车辆路径问题,并采用两阶段蚁群优化算法求解。
综上可以发现:目前多数研究都是利用车辆到达顾客时刻与时间窗的关系来刻画顾客满意度[16-18],这种方式不能很好区分顾客的差异性;假设车辆行驶速度恒定不符合实际情况;假设任意两个客户点之间存在唯一路径也与实际情况不吻合。针对这3个问题,做了3点改进:1)评价顾客满意度时,除了以时间窗作为评价依据外,还考虑了顾客优先级因素;2)任意两点之间存在多条可选择路径;3)在同一道路上,车辆行驶速度与通行时间有关。考虑以上速度变化和多路径选择问题,以同时满足顾客满意度最大和总配送成本最小为目标建立模型,对蚁群算法进行了有针对性的改进,最后通过算例分析验证了该模型的合理性和算法的有效性。
1 建立模型
1.1 问题描述
某配送中心为客户提供配送服务,配送车辆服务能力有限,路网上任意两点之间存在多条路况不同的路径,且同一路径上车辆的行驶速度随通行时刻的不同而变化。配送车辆从配送中心出发,在规定时间窗内对客户进行服务,完成对最后一个客户的服务后返回配送中心。每个客户都有设定的服务时间窗和需求量,且客户具备不同优先级,目标是设计配送路线,用最少的车辆在规定时间内完成所有配送任务,实现最小化配送成本和最大化客户满意度的目标。
1.2 顾客满意度
假设车辆h到达顾客i的时间为Tih,顾客i希望的服务时间窗为[ETi,LTi]。从时间窗角度,顾客i的满意度函数可表示为
(1)
以时间窗衡量的全部顾客的平均满意度为
(2)
其中,xih为0—1变量,表示车辆h是否服务顾客i;|I|为需要服务的顾客数量;I为所有顾客集合。
从优先级角度出发,顾客i的满意度可以用分段函数式(3)表示。
(3)
以优先级衡量的所有顾客的加权平均满意度描述为
(4)
其中,priori为顾客i的优先级,Prior∈{1,2,3,…,r}。利用权值因子判断法,得到以时间窗刻画的顾客满意度和以优先级刻画的顾客满意度所占权重,满意度可以表示为加权和形式:
f=ω1afTW+ω2fp
(5)
1.3 时变速度与路径选择
一般来说,车辆的行驶速度是时变的。为了简化计算,将通行时间段进行合理分割,在每个时间段内假定车辆匀速行驶。假设根据实际情况,将通行时段分成m段,将道路分成n种类型,如表1所示。
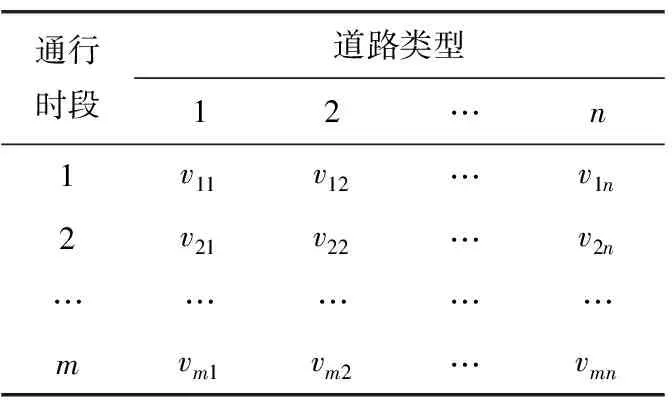
表1 道路类型、通行时段与速度的关系
对于选定客户点j,从客户点i出发有r条路径可到达,对每条路径上的行驶时间分别进行计算。假设车辆h在时间区间为[Ta-1,Ta]的时间段a中的时刻Tih从客户点i出发,经过道路类型为b的路径到达客户j,则通过分段计算车辆从客户点i出发到达下一个客户点j的时刻。车辆h从客户点i到达客户点j的时刻可以表示为:车辆h到达点i的时刻加上需要在点i停留的服务时间以及经过路段所需时间,即Tjh=Tih+Ti+tijh。比较通过不同路径到达客户点j的时刻,为车辆从客户点i到客户点j选择合适的路径。
1.4 模型建立
此模型有两个目标函数:
Maxf=ω1afTW+ω2fp
(6)
MinQ=C1+C2+C3+C4
(7)
式(6)表示最大化顾客满意度,式(7)表示最小化成本。由于f的值在0~1之间,为了整合目标函数,公式(6)可以转化为
(2) 当任一汽机遮断时,为保证主蒸汽母管不超压、不超温,同时热网供汽不中断,可将主蒸汽母管至热管网减温减压电动调门超驰至一定开度,再投入自动控制来兼顾主汽和供汽稳定,调门超驰开度由汽机遮断前的负荷来确定。汽机遮断快速减负荷控制流程如图1所示。
Min (1-f)
(8)
式(7)由两部分组成,分别为:车辆的固定成本和可变成本。车辆的固定成本用式(9)来表示,可变成本随着汽车行驶里程数、实际行驶时间以及为客户点服务的等待时间的变化而变化,可分别表示为式(10)~(12)。
C1=pq
(9)
C2=q1s
(10)
(11)
(12)
其中,p为使用车辆数,q为每辆车的固定费用,q1,q2,q3分别为单位路程(时间)内产生的车辆可变成本,xih为判断车辆是否为顾客提供配送服务的0-1变量。总路程s可表示为
(13)
为消除满意度和成本的数量级差距带来的影响,公式(14)对两者取对数,再用加权方式将多目标优化问题转化为单目标优化问题。对应的加权系数分别为δ和1-δ,其中δ∈(0,1)。
MinδlgQ+(1-δ)|lg(1-f)|
(14)
s.t.
(15)
(16)
Qh≤Ch,∀h∈H
(17)
(18)
(19)
(20)
(21)
(22)
(23)
其中,式(14)表示综合最小成本和最大总体满意度的目标函数;式(15)表示所有车辆的容量需要满足配送总量;式(16)表示车辆h的实际载重;式(17)表示车辆的实际载重不能超过车辆的最大容量;式(18)表示同一个需求点只能被服务一次;式(19)表示配送过程中每辆车只能使用一次;式(20)表示每个需求点只能被一辆车服务;式(21)表示每辆车至少要为一个需求点服务,这里H′表示配送过程中使用车辆的集合;式(22)和(23)为相应的0、1决策变量。
2 算法设计
蚁群算法最早由意大利学者Marco Dorigo[19]于1992年提出,通过模拟自然界蚁群觅食行为实现寻优目的。蚁群算法存在搜索时间长,容易陷入局部最优、出现停滞现象等问题,为克服这些缺点,设计了改进蚁群算法。
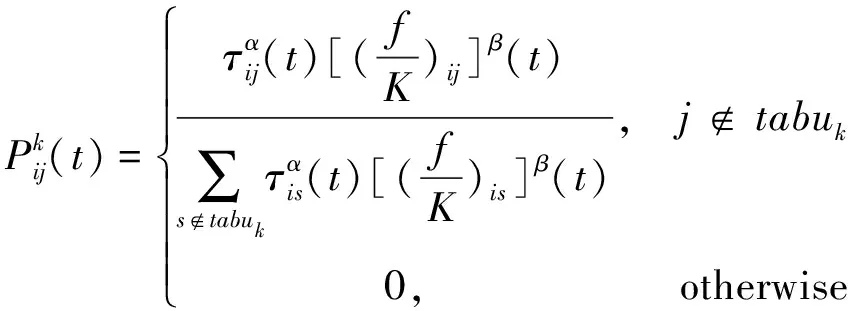
(24)
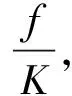
(25)
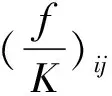
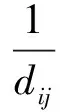
(26)
(27)

(28)
改进蚁群算法流程图如图1所示。

图1 改进蚁群算法流程图
3 算例分析
3.1 实验设置
采用Solomon标准数据集中的RC208算例进行仿真实验。每个需求点的优先级随机生成,配送中心的车辆数和储货容量足够进行所有需求点的配送,所有车辆最大载重量为500。程序采用Matlab R2016a编写,在环境为3.40GHz处理器、16G内存的计算机上运行。算法的参数设置为:最大循环次数iter_max=400;蚂蚁数量m=50;信息素重要程度因子α=1;启发函数重要程度因子β=3。算例中所用其他数据为:ω1=0.6,ω2=0.4,δ=0.5,q=2 000,q1=2.5,q2=0.016,q3=0.048。根据日常车流量的分布将通行时段设置为m=6,道路种类n=3,分别代表3种道路类型(好、普通、差)。对照实验有两组:第1组是不同目标函数的对照实验,说明设计“成本+满意度”目标函数的必要性;第2组是可选路径的对照实验,说明可供选择路径的存在的必要性。同时,用改进算法与原算法比较,证明了改进算法的有效性。
3.2 目标函数对实验结果的影响
本次对比实验分为3种情况:以“成本+满意度”作为目标函数、仅以成本作为目标函数和仅以满意度作为目标函数。由于所求得的是近似解,所以每次运行的结果有所差异,针对每种情况分别进行30次独立仿真,取其中最接近平均值的单次仿真结果进行比较。

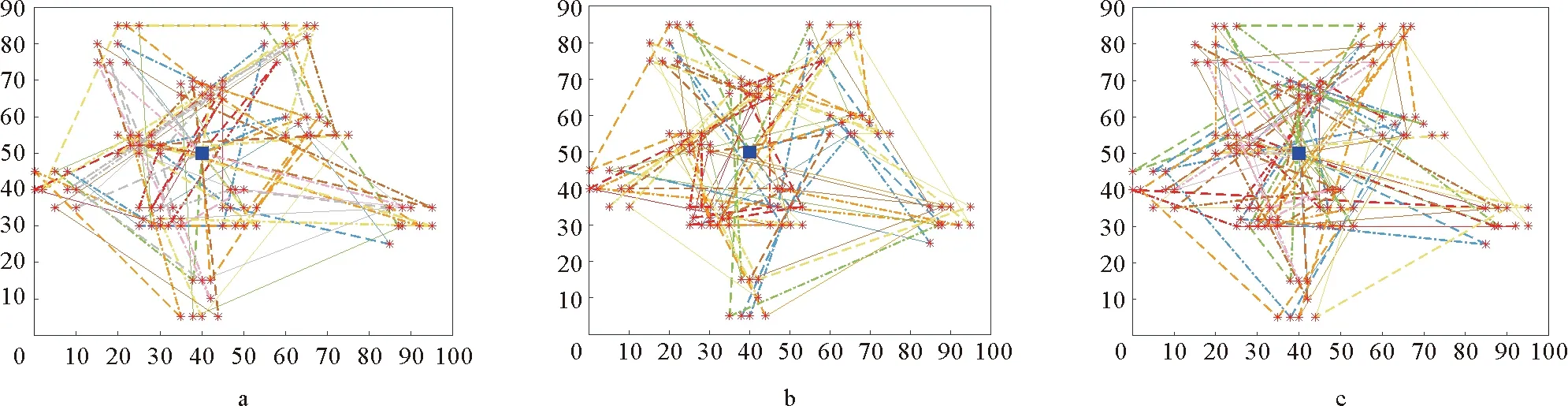
图2 3种情况下的平均最优路径规划
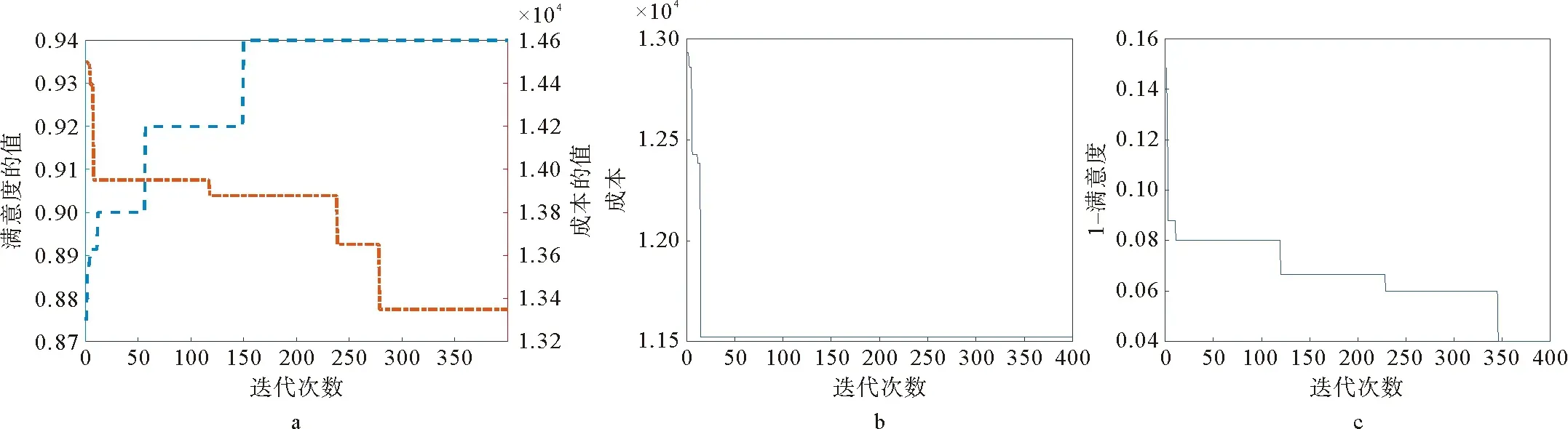
图3 3种情况下的目标函数适应度曲线
当目标函数为“成本+满意度”时,得到最优解所用成本为13 349,满意度达到94%。当目标函数仅考虑配送成本时,相比目标函数是双目标的结果,完成配送所用的车辆数有所下降,成本降低13.7%,顾客满意度下降8.5%,这种情况是以顾客满意度的下降为代价来降低企业的配送成本。当目标函数以顾客满意度为唯一标准时,完成配送所用的车辆数明显增加,用来尽可能满足各个需求点时间窗的要求;配送成本比“成本+满意度”为双目标函数的情况下上涨25%,同时满意度上升2.1%。这表明仅考虑满意度的方案为尽可能提高满意度不计成本代价,故此方案不可行。以上比较结果列举如表2所示。综上,从权衡企业和顾客双方利益考虑,模型中采用“成本+满意度”的模式是值得借鉴的。
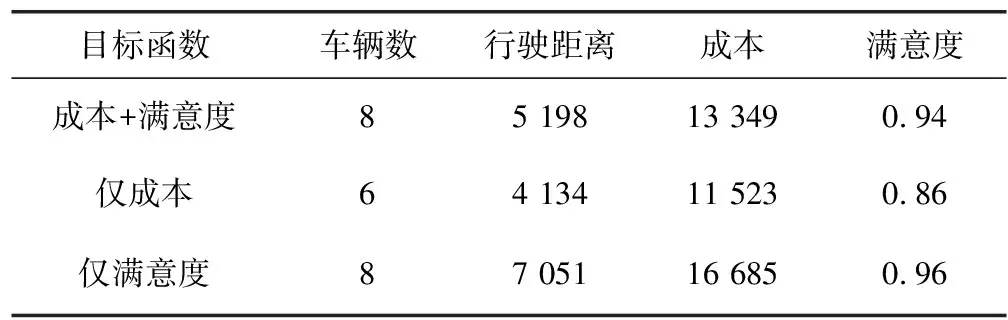
表2 3种情况下平均成本与满意度的比较
3.3 可选路径对结果的影响
为了说明可选择路径的存在对实验结果的影响,假设任意两点之间存在唯一的情况与存在可供选择路径的原模型作对比。表3结果显示其他条件相同的情况下,可供选择路径的存在能够大幅度增加顾客的满意度。与具有可选择路径的原模型相比,单一路径只能通过不断调整配送顺序来实现最小化配送成本和最大化满意度的目标,因此具有可选择路径的原模型满意度是最大的。对于其他参数与具有可选择路径的原模型相比,当模型中仅有最短路径或中间路径时,行驶距离减少,成本随之降低;当模型中仅有最长路径时,行驶距离增加,对应成本上升。
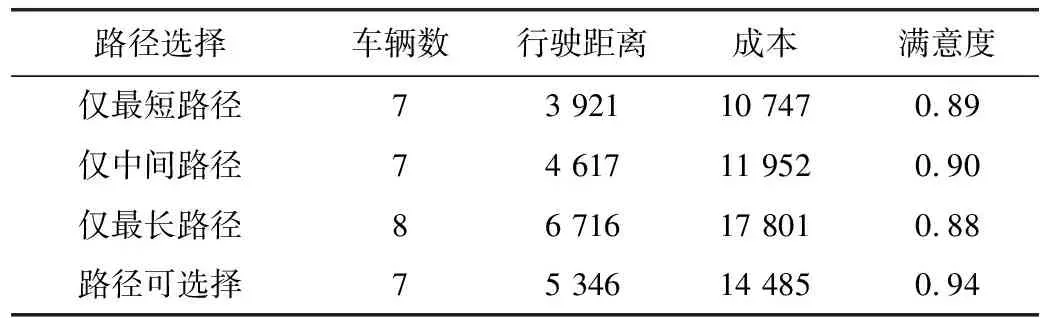
表3 单一路径模型与多路径原模型比较
3.4 改进算法对结果的影响
以上对照实验说明在企业的物流车辆路径问题中,建立考虑成本与顾客满意度的双目标规划模型,提供可选择的道路交通网络,对于降低成本、提高顾客满意度有十分明显的效果。为了验证改进后算法的有效性,用改进前算法对模型再次进行求解,结果对比如图4a所示。改进后的算法收敛速度明显增加,目标函数值也得到较好改善。同时,通过改进蚁群算法检测顾客优先级的差异,首先满足优先级较高的顾客所要求的时间窗。通过图4b的对比,可以发现满足时间窗的顾客点所占比例为94%,且顾客优先级越高,满足时间窗的顾客数目所占比例越大。
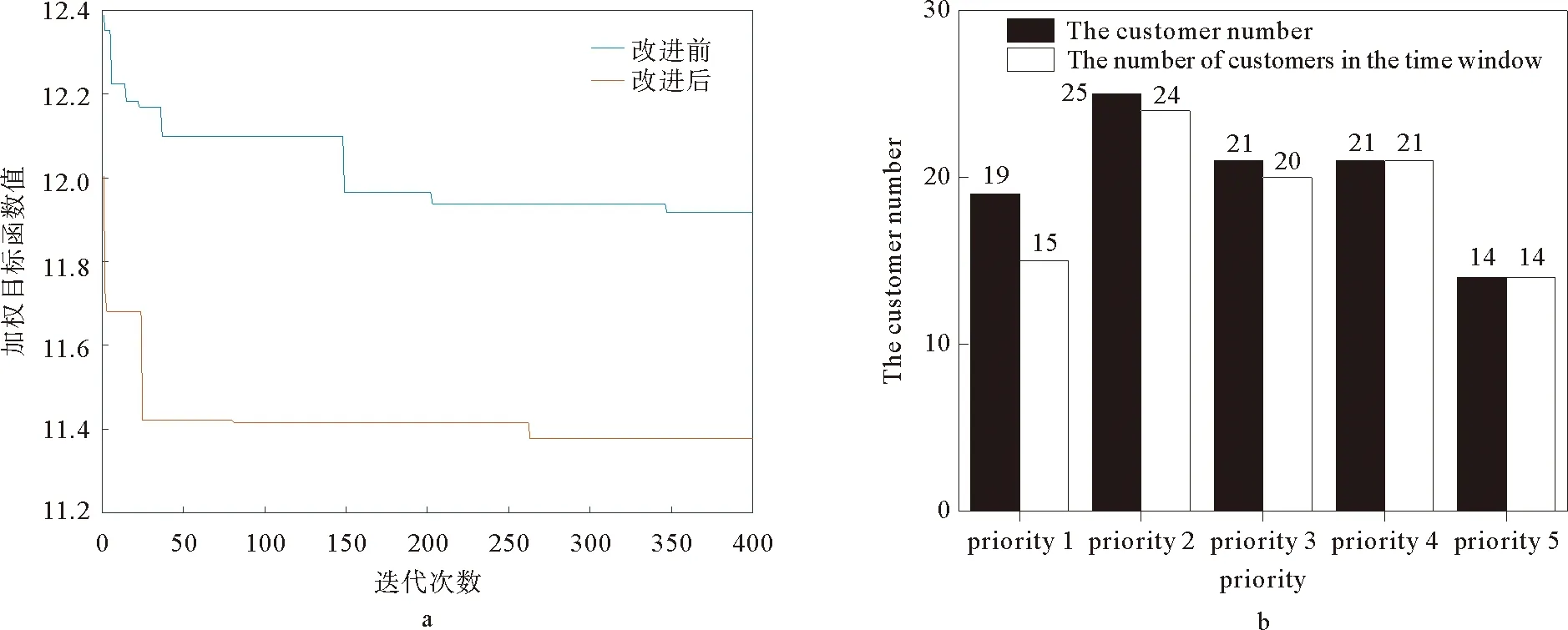
图4 算法改进前后对比
4 结论
本文研究了路网中任意两点之间存在多条路径选择的带时间窗和能力约束的变速车辆路径问题,建立以总成本最小和客户总体满意度最大的双目标混合整数规划模型,利用改进蚁群算法对模型进行求解,仿真实验结果表明所提的模型和算法是有效的。本研究仍存在一些需要改进的内容,如车辆行驶速度的描述不够细致、理论分析有待加强,这些都是下一步要继续研究的内容。

