社交网络中多领导者观点的博弈建模分析
闫晓雪,纪志坚
(青岛大学 a.自动化学院;b.山东省工业控制技术重点实验室,山东 青岛 266071)
0 引言
随着信息技术特别是人工智能、互联网、大数据、云计算和移动通讯等的快速发展,“信息—物理—人类(CPH)”三个系统之间的耦合越来越密切,为人机融合网络系统中的调控带来一系列新挑战。社交网络是多智能体系统[1]和复杂网络系统[2]理论中一个重要的研究方向。通过对观点动力学模型[3-4]的研究阐述了人类行为,进而预测一个社交网络中观点的演变,同时阐明了个人的动态如何塑造复杂的团体行为。因此,观点动态和决策这两个复杂的社会过程是深刻交织在一起的,分析博弈关系能有效揭示生物种群间和生物体间的行为规律以及人类相互作用的行为规律。近年来,人们把工作聚焦在多主体博弈行为的研究上,将博弈控制作为社交网络研究的一个切入点。博弈控制系统[5]将博弈论与控制论结合为一个具有层级结构的调控系统,上层为宏观调控变量,下层为相互关联且功能不尽相同的多个主体。控制论创始人诺伯特-维纳在1948年出版的奠基性著作《控制论》[6]中论述过博弈过程中学习与适应的重要性。从自适应控制理论发展的半个多世纪来看,它为自适应博弈理论的研究提供了基础,近年来相关研究也不断展开[7-10]。此外,纳什均衡概念[11]为一般博弈系统的研究提供了重要工具。多主体博弈控制系统是多个智能体组成的集合,它的目标是将大而复杂的系统转化成若干个小的且彼此相互通信协调、易于管理的系统。本文利用动态规划最优性原理,推导出性能泛函的极小值满足的条件—哈密尔顿-雅克比-贝尔曼(HJB)方程[12-14],通过求解该方程得到最优控制。主要工作为三部分:1)对社交网络群体提出了一种新的划分方式,根据智能体在社交网络中担任不同的角色进行划分,再通过模拟评估每个智能体对问题讨论的综合影响力更新智能体的社会影响力;2)简要回顾经典的DeGroot模型和Friedkin-Johnsen模型,在此基础上加入多领导者博弈控制策略,提出了一个新的观点动力学模型;3)为使问题获得最优的解决方案,建立了耦合的HJB方程,通过求解使得新建的动力学模型获得最优控制策略,最终收敛后达到预设目标。
1 预备知识
1.1 图论
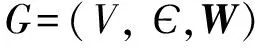
1.2 DeGroot模型和Friedkin-Johnsen模型
经典的DeGroot模型描述了n个智能体观点形成的过程,每个智能体的意见代表了他/她对某一问题的认知取向,由xi=[x1,x2,…,xn]T表示,交互的社交网络用非负影响矩阵W表示。动力学系统模型为
(1)
其中,W=(wij)∈Rn×n,wij>0表示vj对vi观点的影响程度;wij=0表示vi没有从vj获得关于观点的信息。
引理1(本原矩阵[15]) 图G(W)是强连通非周期的,当且仅当W是本原矩阵。
定义1(收敛性[3]) 若模型(1)满足对任意初始观念x(0),存在极限
(2)
则模型(1)是收敛的。即如果对于任意初始条件x(0)有x1(∞)=…=xn(∞),则这个模型达成共识。
对于所有初始观念x(0),如果系统(2)收敛到x(∞)=α1n,α∈R,则意见最终达成一致。在文献[16]中总结了模型(1)的收敛条件。
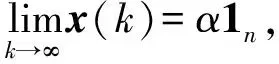
DeGroot模型的一个推广模型是在文献[17-18]中提出的Friedkin-Johnsen(F-J)模型。表示为
xi(k+1)=ΛWxi(k)+(In-Λ)xi(0),i=1,2,…,n
(3)
其中,对角线矩阵Λ=diag(ξ),ξ=(ξ1,ξ2,…,ξn),ξi∈[0,1]代表智能体i对社交网络影响的敏感度,当Λ=In时,F-J模型将变成DeGroot模型。对于强连通网络,有以下收敛结构。
引理3[19]假设图G(W)是强连通的,并对∃i,j∈{1,…,n}有ξi,ξj<1,那么ρ(In-ΛW)<1且式(3)收敛至
(4)
矩阵V(In-ΛW)-1(In-Λ)是行随机矩阵。因此,x*的观点为x(0)的凸组合。
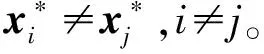
2 动态社交网络模型
2.1 模型的建立
根据术业有专攻的特点,让擅长者担任领导者去做主导工作,其他个体作为跟随者提供改进和完善工作,这样设计符合实际社交网络的设定。在F-J模型中加入博弈策略,并设计成以多个领导者为主体的博弈控制系统,使其观点形成的解决方案能更好地解决问题。系统动力学模型表述如式(5):
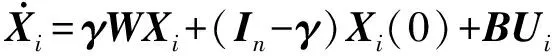
(5)
其中,W∈Rn×n,B∈Rn×m,C∈Rm×n,Xi∈Rn表示智能体i的观点向量,γ=diag(β),βi∈[0,1]表示智能体i对社交网络影响的敏感度,Ui∈Rm是领导者i的控制输入策略,Υi∈Rm将领导者的观点不断提取出来。
为便于分析,借鉴Stackelberg-Nash均衡博弈的特点,预先确定理想目标Zi∈Rm定义误差矢量δi为
δi=Zi-Yi
(6)
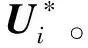
(7)
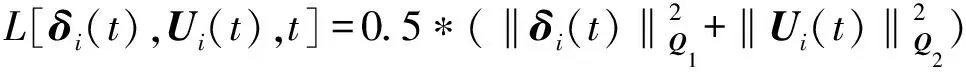
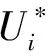
为保证定义2多领导者博弈控制可获得问题的最佳解决方案,本文建立多个领导者为主体对智能体进行新的划分,将大而复杂的系统转化成若干个具有强连通结构的观点群体系统。
2.2 智能体的划分
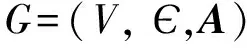
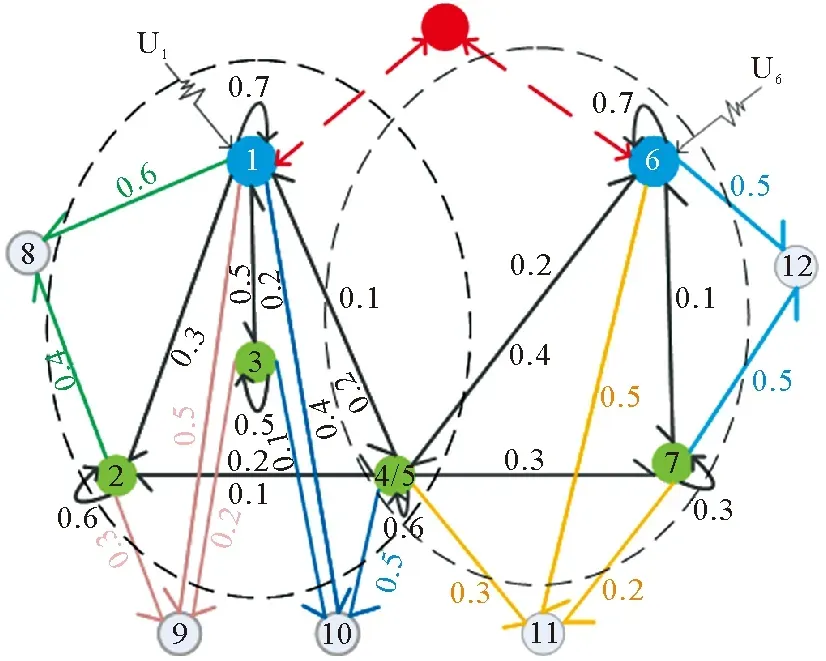
由图1来模拟一个有限个个体的实际社交网络交互情况,每个智能体根据观点和相互之间的拓扑结构图来确定其角色。蓝色、绿色和灰色分别表示领导者、跟随者和外围跟随者。此外,系统模拟智能体的观点被多个领导者采纳,经验证这不会产生冲突也不会改变观点的性质,仅使结构图交互变得更复杂,解决办法是被几个领导者采纳就将该智能体看作几个节点,进行拆分。
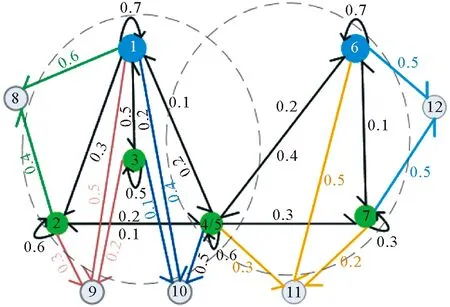
图1 由11个智能体组成的交互社交网络拓扑结构图
为便于分析,图2就是对拓扑图进行等价拆分,化简为若干个以每个领导者和与之相关联的跟随者形成的强连通图,当不同的领导者采纳了同一个跟随者的观点时,该跟随者将参与到不同领导者小组的讨论中。

图2 领导者-跟随者影响网络拓扑结构图
由图1写出加有外围跟随者的拓扑结构图的影响矩阵A为
当结构不足写出方阵时矩阵右侧补零,可得含外围跟随者的影响矩阵A的紧凑形式。
(8)
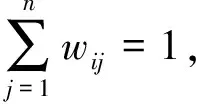
引理4[4]假设领导者—跟随者形成的矩阵W满足ξi>0且G(W)中不包含完全由非固执节点组成的独立强连通分支,则F-J模型在问题上能达到一致,当且仅当图G(W)中存在一个部分固执节点,该节点具有到其他所有部分固执节点的有向路径。
根据引理3和4可得推论1和定理1。
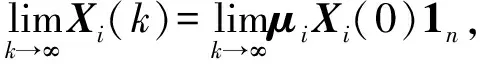
定理1当影响矩阵G(W)具有公式(8)的结构时,它的主导左特征向量的取值只与块矩阵Wlif有关,与块矩阵Wliff无关。
证明:将矩阵(8)的紧凑形式展开为矩阵(9)构成下三角结构的分块矩阵,其中s为领导者的个数。
(9)
由分块三角矩阵的性质可得,分块三角矩阵的特征值等于对角线上矩阵的特征值。假设A的主导左特征向量与块矩阵W有关。下面将主对角分块矩阵化简为W=diag([Wl1f…Wlsf]),Wlif存在一个特征值为1且其左特征向量为主导左特征向量,即满足ξiWlif=ξi
(10)
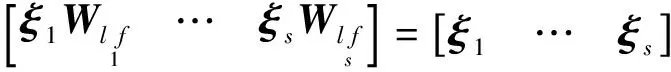
(11)
因此,每个Wlif块矩阵形成,通过线性组合将式(10)推到式(11)。假设成立。
假设A的主导左特征向量的取值与块矩阵Wliff有关,且保证每一个块矩阵Wliff是方阵,那么可得

因此,当块矩阵Wliff是方阵时,系统的左特征向量ξliff为零。故A的主导左特征向量的取值与块矩阵Wliff无关,且每一个块矩阵Wliff不必须是方阵,符合实际的社交网络。综上所述,定理1成立。
由引理1可得对于一个具有强连通结构的行随机矩阵,存在一个单特征值为1且与特征值1相关的特征向量是矩阵的主导左右特征向量。由图1和矩阵A可以看出外围跟随者对产生观点的智能体进行了评估,可得如果社交网络系统出现外围跟随者,加零矩阵补齐为方阵形成行列相等的行随机矩阵(8)。又因为仅使用左特征向量不能完全公正地表达出该社交网络中智能体的相对贡献。由此引出定义3。
定义3在一个包含外围跟随者的社交网络中,将包含领导者—跟随者的加权有向图G(Wlif)的左特征向量ξi和包含外围跟随者的加权有向图G(Wliff)进行凸组合,表达整个社交网络中产生观点的智能体i对社交网络影响的敏感度,即对角阵γ
(12)
其中,γ=diag(β),βi∈[0,1],i表示产生观点的智能体,m为每个强分支中外围跟随者的数目。
2.3 问题的最优同步解决方案
这一部分的研究目的是从动态规划和最优控制[20]中推导出最优控制策略。
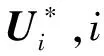
通过系统(5)建立耦合形式的HJB方程,求得定理2中的最佳领导者响应策略。根据极小值原理可写出哈密尔顿函数:
(13)
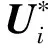
由于Q2是正定矩阵,得
(14)

(15)
终端条件
(16)
联立公式(5)和公式(15)可得方程(17):
(17)
λ=PXi-Γ
(18)
其中,P和Γ是λ关于Xi的变换矩阵,P是n×n维矩阵,Γ是n×1维矩阵。


(19)
Γ是下列一阶微分方程的解,且必须满足式(16)的终端条件可得:
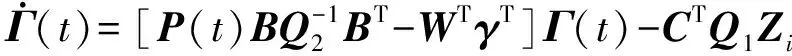
(20)
解出P和Γ,将式(18)代入式(14)可求得:
(21)
基于Friedkin-Johnsen模型渐进稳定的条件,矩阵W是行随机矩阵,对角阵γ满足0<γ (22) 将第2节图1的交互社交网络拓扑结构图进一步完善,如图3所示。 图3 社交网络由外部控制器(红色节点)驱动领导者1、6的拓扑结构图 性能泛函中的权重矩阵Q0=diag{2.6;2.6},Q1=diag{0.01;0.01},Q2=diag{2;2}。所有产生观点的智能体初始观点矢量在0到10之间,随机选择Xi(0)=[7;5;4;5.5;5.5;7.5;4.2]T。 当预设的理想目标为同一目标Zi=[8;8]时,系统观点状态Xi的收敛图,如图4所示;领导者控制策略Ui,i=1,6的变化曲线,如图5 所示;系统误差δi变化曲线,如图6所示。在图4中还可以看出跟随者4、5为同一节点,当被不同的领导者采纳意见时,它们的观点在融入过程中被采纳了不同的部分,使得每一个以领导者为主体的观点群体最终都获得了理想目标的最优解决方案。 图4 在同一目标下,系统观点状态的收敛图 图5 在同一目标下,领导者1,6控制策略的变化曲线 图6 在同一目标下,系统误差变化曲线 当预设的理想目标为不同目标Zi=[7;8.5]时,其他保持不变的情况下可得系统观点状态Xi的收敛图,如图7 所示;领导者控制策略Ui,i=1,6的变化曲线,如图8所示;系统误差δi变化曲线,如图9 所示。图7中还可看出领导者1的最初观点和理想目标一样,但在结合跟随者2、3、4的观点进行再优化时产生了区分,最终分别为最佳解决方案提供了可采取的观点。 图7 在不同目标下,系统观点状态的收敛图 图8 在不同目标下,领导者1,6控制策略的变化曲线 图9 在不同目标下,系统误差变化曲线 本文通过多领导者博弈控制考虑了社会主体协作的影响力,对此进行建模和仿真使其更有效地分析社会网络中从局部交互到全局协调的情况。本文还对观点的权重进行分析,当同一个观点被不同的网络群体中的领导者采纳的时候会将观点划分到多个群体中,这种对智能体划分的方式将为社交网络打开一个新的视角,可以建立更加复杂的交互社交网络。最后还实现了当目标控制器对不同的领导者有不同的标准时,系统也可以最终达到理想目标获得相应的解决方案。将来会进一步研究同一个智能体的观点在不是非正即负的情况下如何更加细化拆分获取信息,每个智能体在本次问题中的影响力在下一个问题讨论时又会产生多大的影响,并建立反馈机制。3 仿真结果



4 结语

