民航多点定位系统基站布局优化

赵向程 高 锋 甄 然 吴学礼

(河北科技大学电气工程学院 河北 石家庄 050018)(河北省生产过程自动化工程技术研究中心 河北 石家庄 050018)

0 引 言

随着我国空域交通的不断复杂，对各类飞行设备的定位精度要求也越来越严格[1-2]，自动化监视数据处理已成为空中交通管制的重要依据和手段[3-4]，而多点定位系统是目前最先进的民航机场监视手段，它具有极高的定位准确性、刷新频率高、稳定性好等特点[5-7]。目前，多点定位系统正在替代传统的定位方法成为大型机场的主要监视手段[8]。当卫星导航定位在天气不佳时，MLAT系统(多点定位系统)就显得尤为重要[9]。为提高定位精度，致力于飞行事业的众多国内外专家学者始终坚持在科研的第一线，如利用遗传算法对MLAT系统的信号传播路线进行改良，与普通激光检测设备比较，优化后的设备明显提高了目标的识别精度[10]。段凯宇等[11]提出了基于TDOA/AOA的卡尔曼滤波算法，仅计算一次加权最小二乘法即可，简化了计算过程且消除了根的模糊解。李家蓬等[12]提出了利用自适应遗传算法来进行地面基站的布置，提高了监视区域内飞机的定位精度，可见地面基站相对于目标的几何关系对多点定位系统的定位精度有着不可小觑的影响，传统的布置基站方式通常以星形、T形等固定形状布置基站，这样达不到全局最优的布置基站方式[13]。由判断定位精度的GDOP和免疫寻优算法的寻优过程[14-16]，本文提出了以GDOP数值工具为评判标准利用免疫寻优算法计算基站布局的方式来提高多点定位系统的定位精度。

1 问题描述

1.1 MLAT系统基站检测定位过程

采用到达时间差(TDOA)针对机场内所有装备了统一模式信号的应答机的设备进行定位。因为4个地面接收站的空间位置已知，所以目标信号到各基站的到达时间(TOA)传输到主站进行计算得到TDOA后可以检测出目标的位置，整个定位过程不需要基站与目标间保持较高的时钟同步。检测目标的基站布局及检测原理如图1所示。

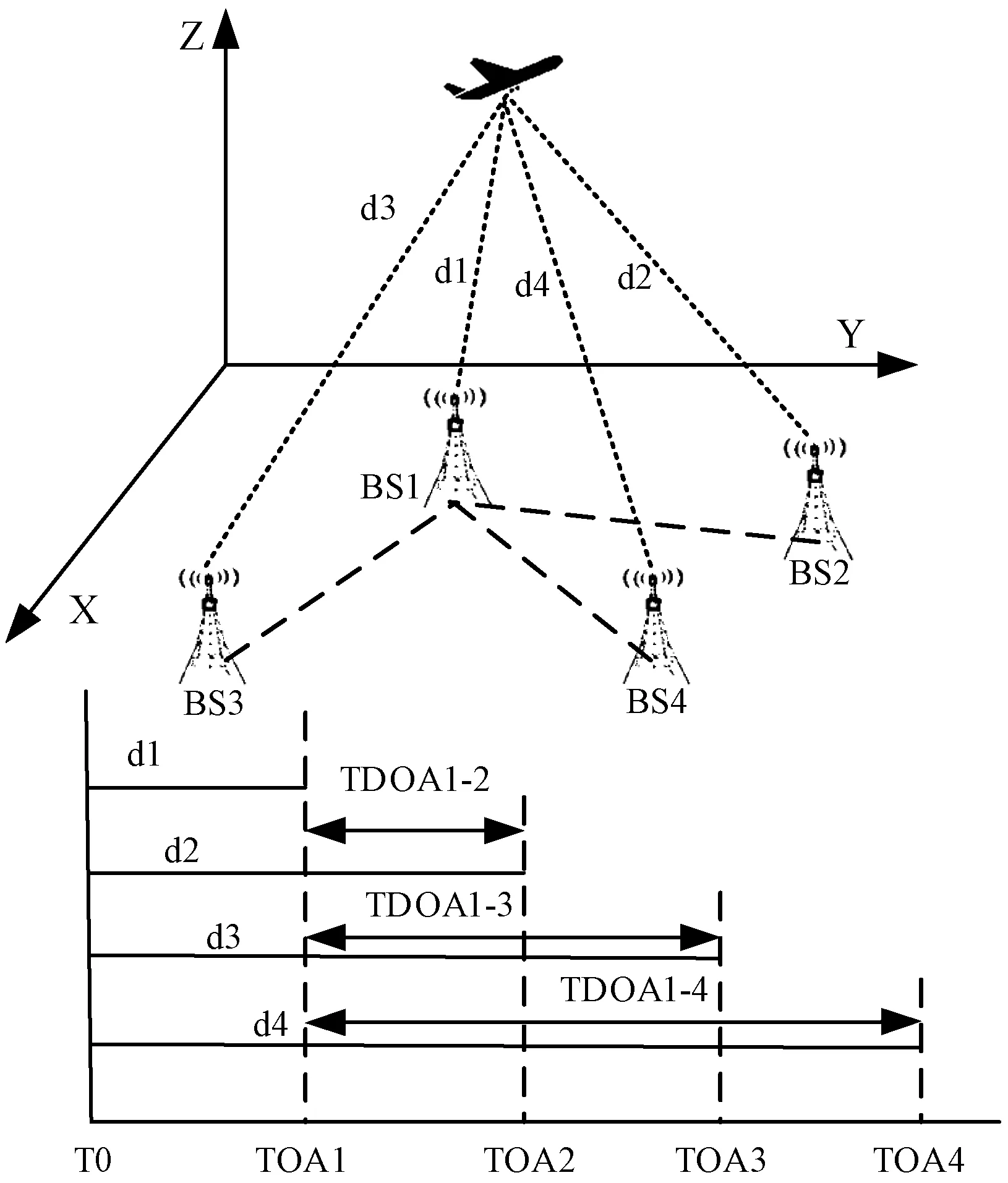
图1 多点定位系统定位原理

计算过程为：

(1)

图1中，BS1-BS4表示MLAT系统的检测基站，BS1为主站，其他3个基站是副站。假设飞行目标位置为(x,y,z)，4个基站位置为(xm,ym,zm)，dm表示飞机到第m基站的距离，dm,1表示信号到第m基站与主站的距离差，即dm与d1的差值，c表示信号的传播速度，nm,1表示信号到达m基站与主站的时间差，即(dm-d1)/c。

1.2 多点定位系统基站布局模型

地面基站相对于目标的几何关系对多点定位系统的定位精度造成很大影响，在4个基站的几何中心位置，定位精度最高，而检测区域的边缘定位精度相对较低。所以基站的布局对于目标的相对位置发生变化，TDOA方程的计算参数也会发生变化，最终会严重影响对飞行目标的定位精度。以GDOP为评判定位精度的标准来设计基站布局就尤为重要。假设机场监测区域为10 000 m×10 000 m，x方向和y方向都以100 m为间隔将监视区域分为100×100个极小的方块。每个小块的中心点就是基站的预设点，从这些点中选出一个主站和三个副站作为一个布置基站方案。然后计算GDOP的均值，其值的大小就代表着基站布局方案的优劣，值越小，定位精度越高。用自然数对地面基站的空间位置标记，即每个坐标都有对应的序号，具体如图2所示。

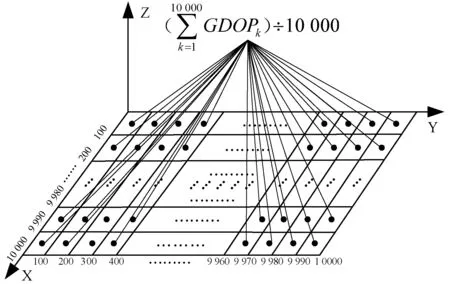
图2 民航机场基站布局模型

2 基于免疫寻优算法的优化布置基站

针对图2基站布局模型，提出了基于免疫寻优算法计算最佳基站布局的方案。免疫寻优算法比其他寻优算法具有更高群体多样性且能避免“早熟”问题。算法中的抗原是指要解决的问题，抗体表示解决该问题的可行解。算法布置基站的详细流程如图3所示。

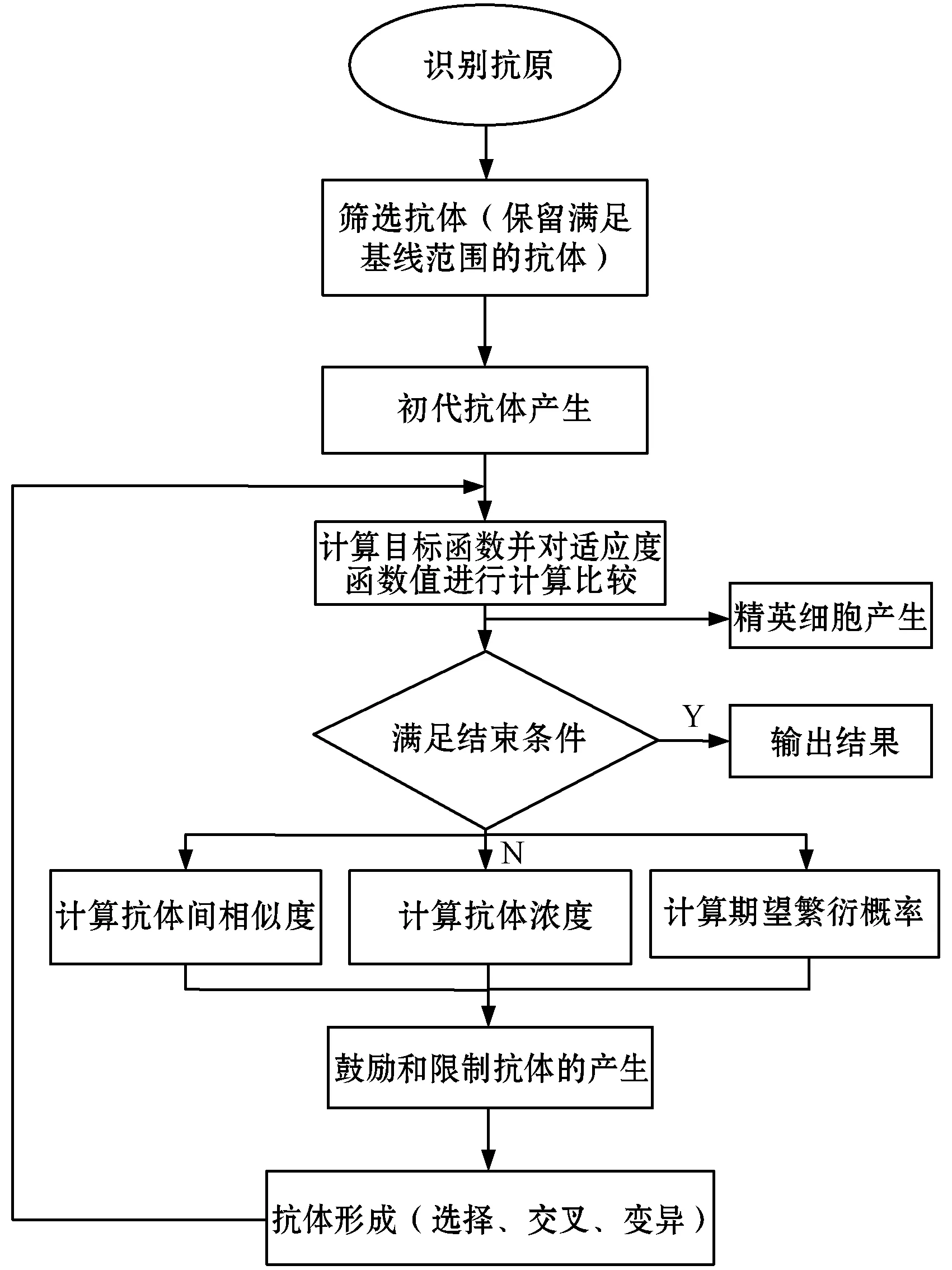
图3 免疫寻优算法布置基站流程

2.1 免疫寻优算法布置基站的寻优过程

免疫寻优算法中初始种群是由随机产生的个体与精英库中的个体形成的。当有精英细胞时，初始种群从精英细胞中筛选产成。反之，可以在整个检测区域内随机选择四个点来形成个体，再重复选择产生初始抗体群。以抗体的平均繁衍概率为标准对群体中的抗体进行评判，取初始抗体群中平均繁衍概率最高的前X个抗体构成第一代群体，并保留X中的前y个抗体加入精英库中。对个体进行交叉、选择、变异后可得到新的群体，此时的新群体再加上精英库中的个体形成新一代群体。抗体长度为LK(LK表示基站数量)，每次被选为基站的点的序列就是对应的一个抗体，例如:1，2，…，10 000表示预选点的序号，从这10 000个点中选择4个点作为基站，比如[255,300,1 025,4 713]代表一个抗体，同样也表示这是在满足条件下的一个解决方案。每循环一次都会计算适应度函数值并进行比较，保留适应度值最高的个体与精英库中的个体形成新一代群体。整个算法的计算是一个优化的循环过程，最后输出布置基站方式肯定是最优布置基站方式。

2.2 建立免疫寻优算法布置基站的数学模型

根据以上工作流程，可建立免疫寻优算法布置基站的数学模型，主要包括目标函数的计算和满足结束条件的设定、适应度函数的建立、抗体间相似度计算、抗体浓度计算、繁衍概率计算等。

2.2.1目标函数的计算和满足结束条件的设定

由机场基站布局模型，可以建立目标函数的表达式：

(2)

式中：k表示机场内某个基站预设点；n是预设点的总数。

这里设定一个满足结束条件的阈值，即当计算得到的目标函数值小于等于这个阈值时满足结束条件输出结果，本文设定的阈值为10 000。即结束条件为:

f(x)<10 000

(3)

GDOP的计算过程如下：

根据式(1)可知，目标到主站与到第m基站之间的距离差为：

dm,1=dm-d1

(4)

对式(4)两边微分化简可得：

(5)

m=2,3,4

为方便计算可将式(5)写为D=H×L。

其中：

(6)

(7)

设各站的TDOA信号测量误差为D,飞机的坐标定位误差为L,则根据线性代数可以计算L,即：

L=(HTH)-1HTD

(8)

令(HTH)-1HT=C=[bm,j]3×3。

设测量TDOA数据协方差的表达式为：

PD=E[D,DT]=

(9)

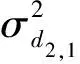
(10)

而多点定位的误差协方差为：

PL=E[L,LT]=C{PD}CT

(11)

紧接着，可以令PL=[hlr]3×3，其中：

(12)

通过公式推导可以得到定位误差在三维坐标上的方差：

(13)

综上所述，GDOP的表达式为：

(14)

2.2.2适应度函数的计算

适应度函数以目标函数为基础，反映了免疫算法优化布置基站过程中的限制条件。由于基线长度对定位精度也有一定影响，基站间基线长度与定位精度成正比，但不能过长，在这样的限制条件下可以把适应度函数设为：

(15)

式中：i,j=1,2,3,4，i≠j；分母中第二项表达式为限制函数，其有效地排除了基线长度小于L的情况，提高了算法的运算效率，在仿真实验中设定L为1 000，∂i,j表示基站i与基站j之间的距离，即：

(16)

适应度函数值越高表示此抗体越接近最优解，即定位精度也越高。

2.2.3抗体之间相似度计算

在判断抗体之间相似度之前，先确定一个相似度判定的阈值limit。组成两个个体的编码有大于等于limit位相同，就判断两个抗体“一致”，反之表示不一致，在这里抗原编码的各个位的顺序不用考虑，可以依据抗体之间相似度值，即：

(17)

式中：samem,n表示抗体m与抗体n相同位的个数；length表示单个抗体的长度。例如，抗体m为[255,7986,1439,5781]，抗体n为[7986,4627,255,8657]，两抗体中有2个数值是一致的，则通过式(17)计算出两抗体的相似度为0.5。

2.2.4抗体浓度计算

抗体浓度指的是种群中大于等于阈值limit的抗体在整个种群中的占比，结合式(17)可以推断抗体浓度的表达式：

(18)

式中：sum表示种群中抗体的总数。

2.2.5期望繁殖概率的计算

在免疫算法中个体的繁衍概率是依据适应度函数和抗体浓度同时决定的，则由式(15)和式(18)可得期望繁衍概率的表达式如下：

(19)

其中c为常数。根据式(13)和式(15)可知，适应度函数值与繁衍概率成正比；抗体浓度值与繁衍概率也成正比。构建此表达式巧妙地鼓励了适应度值更高的个体，同时制约了浓度高的个体，从而确保了种群多态化。如果只是单纯地进行这样的操作会使浓度高并且适应度高的个体受到制约，致使最优方案的缺失。所以还要采取择优保存政策，即精英库的刷新，先将适应度值高的个体放到精英库里，再依据繁衍概率把种群中其他优质个体存入精英库中，这样会有效保留最优解。

3 MATLAB仿真对比实验

3.1 仿真验证免疫寻优算法布置基站

实验1：由机场基站布局模型和免疫算法布置基站数学模型进行编程来验证该布置基站方法的可行性。仿真通过比较适应度函数值和抗体间相似度的大小来决定最优布置基站方案。免疫寻优算法的相关数据设定：种群规模为100，记忆细胞为20，交叉概率为0.45，变异概率为0.5，多样性评价参数为0.95。目标飞行高度对定位精度也有一定的影响，高度越高定位误差越小，所以应选取相对合适的数值来进行计算，在本实验中设置被检测飞机飞行高度为300 m。基线长度对定位精度也有一定影响，基线长度越长定位精度越高，所以在本次仿真中基线长度设定都大于1 000 m。由图4可以看到免疫优化算法在布置基站过程中迭代了35次后目标函数值和平均目标函数值都趋于稳定，表明了免疫优化算法在寻优过程中的收敛性。图5是通过免疫算法计算出的最优布置基站方案，四个方点就是基站的三维位置，菱形点表示飞行高度为300 m的飞机。由于机场内有较高建筑物，所以基站高度统一为5 m。图6是在图5基础上绘制的整个检测区域内的GDOP的分布图。在这里简称该布置基站方案为算法布置基站。

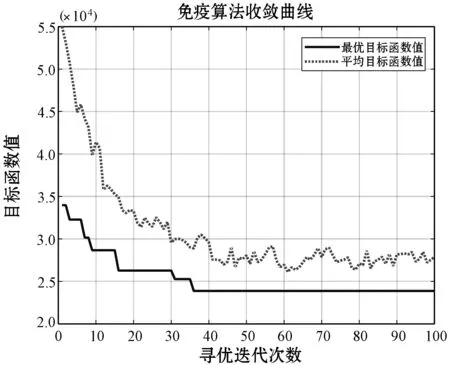
图4 免疫优化算法收敛曲线

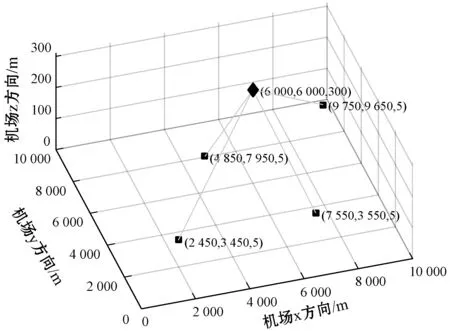
图5 免疫最优布置基站方案

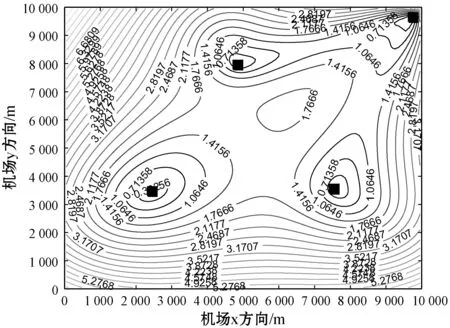
图6 免疫最优布置基站方案的GDOP分布

3.2 对比论证免疫寻优算法布置基站的最优性

通过以上仿真结果我们得到了基于免疫寻优算法的布置基站方案以及其GDOP的分布图。为了证明该算法布置基站的最优性，选择从以下不同角度来进行对比论证。

1) 角度1：与传统固定形状布置基站的仿真对比。

实验2：本实验与实验1的参数设置一致，飞机飞行高度一致，以星形布置基站方式和T形布置基站方式绘制GDOP的分布图如图7-图8所示，这更加直观地令传统的布置基站方式与免疫算法布置基站形成对比。

图7 星形布置基站方案的GDOP分布

图8 T形布置基站方案的GDOP分布

以上实验的基站坐标和GDOP值如表1所示。

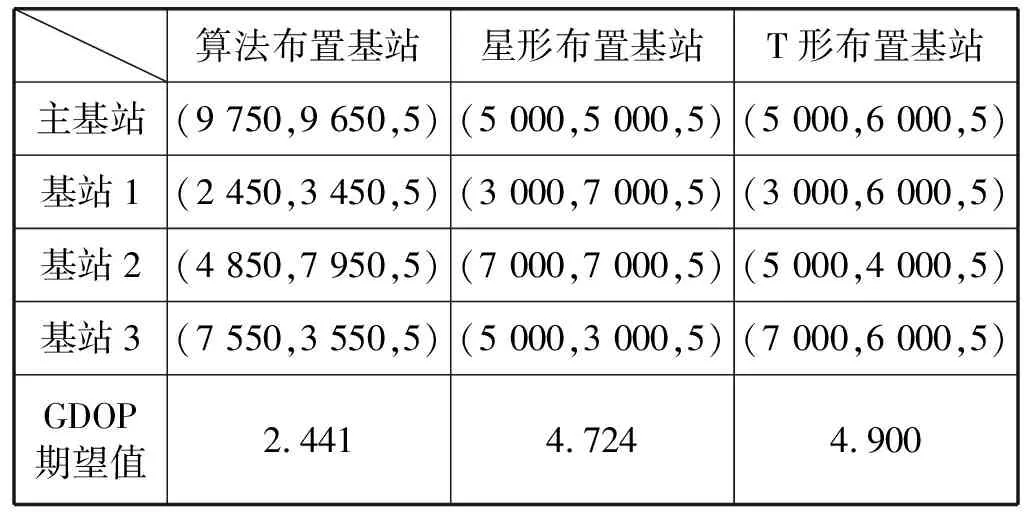
表1 各布置基站方式下基站坐标及GDOP值

分析以上两个实验的数据和GDOP的分布图可以看出T形布置基站方式的定位精度具有方向性，而星形布置基站方式在整片检测区域内的定位精度分布比较均匀，且越靠近主站的区域定位精度越高。所以在知道目标飞行方向的时候可以采用T形布置基站，反之可以采用星形布置基站方式，但是针对民航机场复杂的空中地面交通状况采用T形布置基站显然行不通，所以利用免疫算法计算出最优布置基站方案可以对所有方向的目标定位达到较高的精度，在仿真得到的实验数据中可以直观地看到免疫算法布置基站方案的定位精度比星形布置基站方案提高了48%以上。

2) 角度2：改变算法布置基站方案主站的位置来对比验证。

实验3：本实验与实验1的参数设置一致，目标飞行高度一致。通过实验1的仿真结果可知最优布置基站方案的主站坐标为(9 750，9 650，5)，在图9的13位置上。主站以13为中心向周围24个位置移动，并将每个位置上的GDOP期望值绘制成对比图，更加直观地证明了算法布置基站方案具有更高的定位精度。具体实验结果如图10和表2所示。

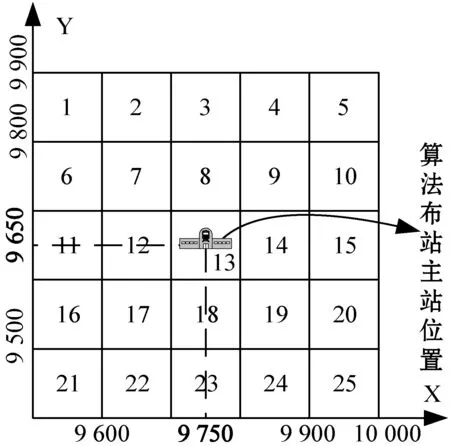
图9 算法布置基站方案主站移动模型

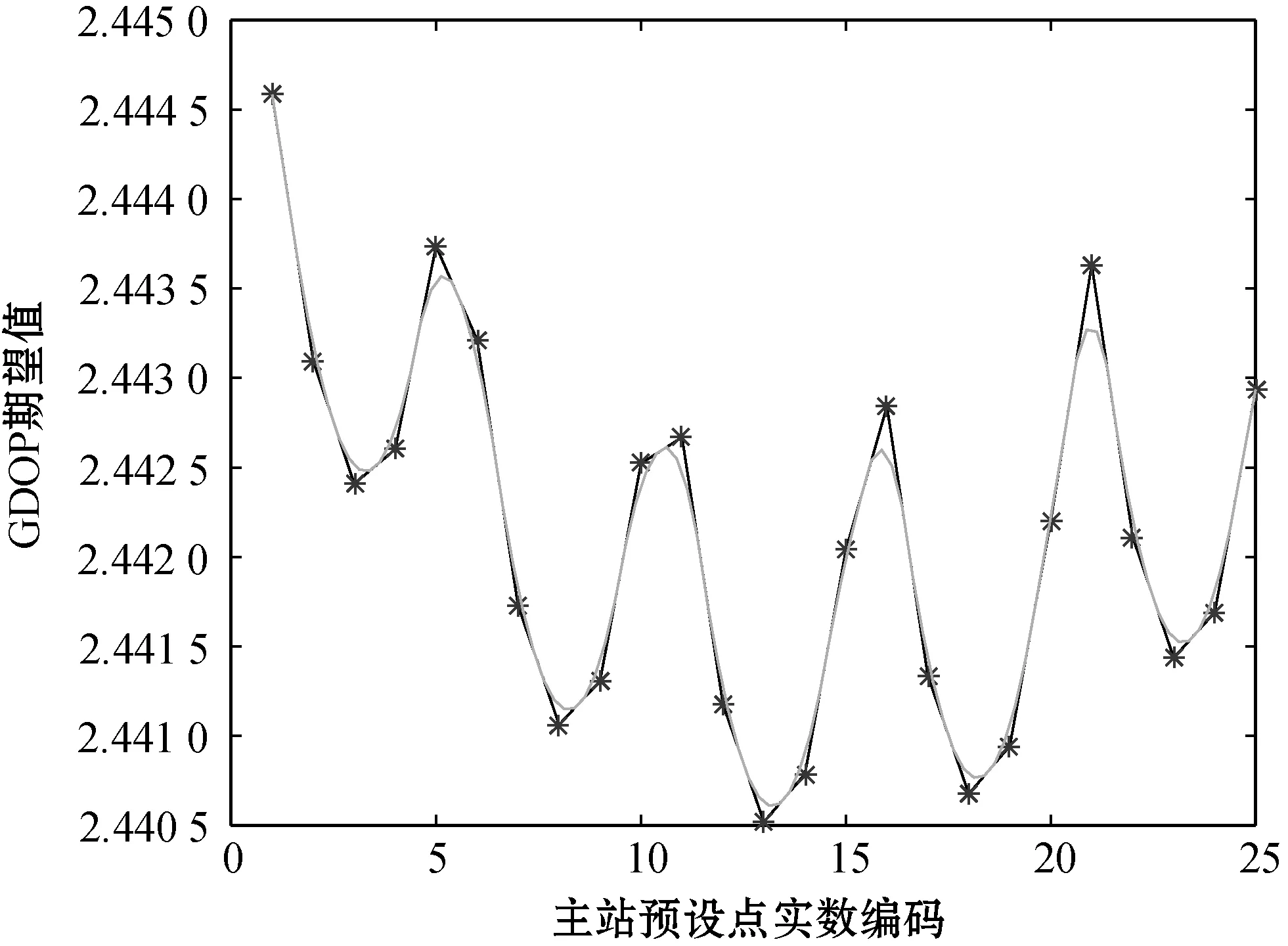
图10 主站在不同位置的GDOP期望值分布图

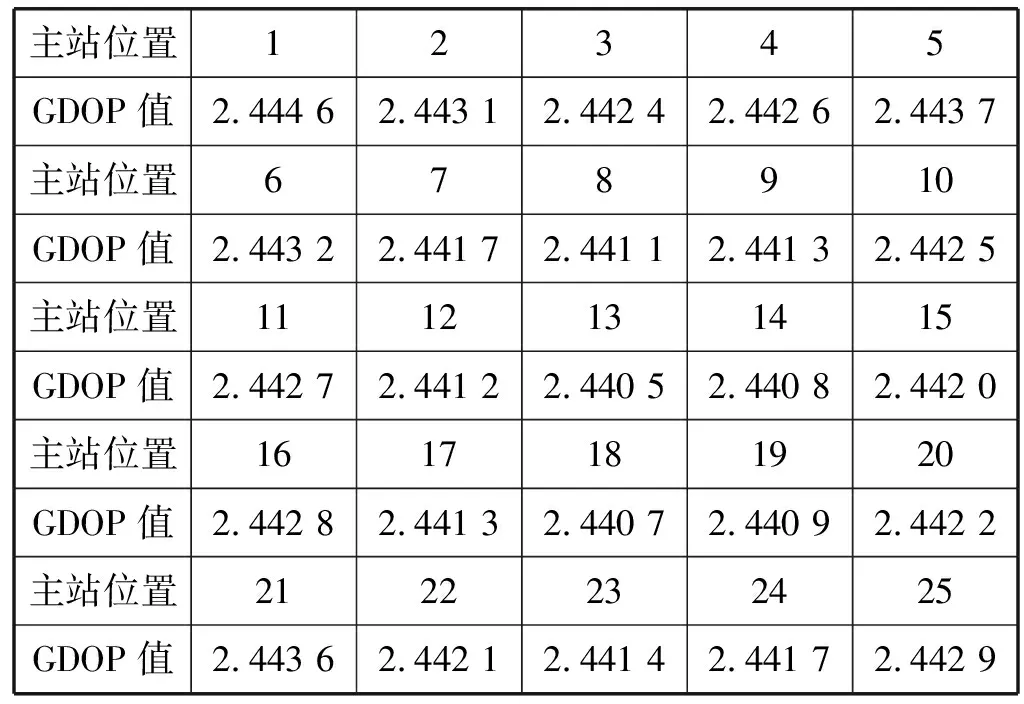
表2 主站在不同位置的GDOP期望值数据

从图10和表2的实验数据可以很直观地看到只有当主站在13上时GDOP期望值最小，这有效证明了免疫寻优算法布置基站方案为最优布置基站方案。

4 结 语

本文主要以提高民航机场场面监视的定位精度为大背景，将免疫寻优算法的寻优过程与多点定位系统的基站布局进行了结合，利用免疫寻优算法对整个机场的检测区域计算选出最优布置基站方案。最终的布置基站方案以GDOP数值工具为评判标准与传统的星形布置基站方式和T形布置基站方式进行对比，同时又在最优布置基站方案下改变主站位置来进行数据对比。三个仿真实验结果强有力地表明了免疫寻优算法布置基站的定位准确性极高，完全满足民航规定的定位精度要求。这为现实中民航机场基站的布设提供了理论依据。今后将在提高民航机场场面监视的定位精度方面做进一步研究。