面向Stacking集成的改进分类算法及其应用

陆万荣 许江淳 李玉惠

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

0 引 言

分类是机器学习与数据挖掘中最频繁、最重要的任务之一。常见的分类算法，如Logistic回归(LR)、K最近邻(KNN)、朴素贝叶斯(NB)、决策树(DT)、支持向量机(SVM)和多感知器神经网络(MLP)等已经应用于各领域，如信用卡欺诈、遥感图像分析、石油泄漏检测和入侵检测等[1-2]。但是之前的研究已经发现这些分类器都存在各自的优缺点，也证实了这些缺点使得模型达到了性能瓶颈。例如，逻辑回归法LR使用灵活、计算成本低、执行效率高，但是容易过拟合；SVM有夯实的理论基础和低错误率，比较适合处理高维数据，但对参数调整和函数选择却比较敏感；DT容易过拟合，对属性取值数量敏感，并忽略了属性之间的相关性；神经网络算法参数众多、解释性差等。同时，由于数据本身存在的问题，如类别不平衡、缺失值、异常值和高维非线性等问题都限制了传统分类算法的进一步发展。

为了解决传统分类算法的缺点以在任务中获得更高的分类精度。分类算法的研究正逐步从单一模型向集成学习(Ensemble Learning)发展，集成算法既能吸纳基模型的优点又能规避它们的缺点。集成学习通过构建并结合多个分类器来完成分类任务[3]，最突出优势就是“博采众长”，通过将多个弱分类器按照一定的方式或策略组合起来形成强分类器，从而在任务中取得更好的预测效果。目前，集成学习按照优化方向可以分为用于减少方差的Bagging、用于减少偏差的Boosting和用于提升预测结果的Stacking三大类[4-6]。Stacking集成算法不仅能够组合传统的LR、SVM和NB等单一分类模型，还能组合Boosting和Bagging生成的集成分类模型，从而实现模型卓越的泛化能力。因此，Stacking集成算法在各个领域得到了广泛的应用。文献[7]提出了基于LR、DT和SVM的Stacking集成模型去建立P2P网贷违约风险识别模型，证实了集成模型比单一算法建立的模型风控性能更好；文献[8]提出了一种多模型性融合的Stacking集成算法进行负荷预测，且在基模型中选择了深度学习算法LSTM，得出基模型学习能力越强，关联程度越低，则Stacking模型预测效果就会越好；文献[9]将Stacking用于自然语言处理领域，将上下文信息作为分类器输入特征向量对中文组块识别，结果表明准确率和召回率相比于投票法(Voting)都有所提高。但是，传统的两层Stacking集成方法都忽略了基分类器输出信息的重要性，没有充分利用新特征与预测结果之间的相关性，导致模型预测能力和泛化能力提升有限。

针对以上问题，本文选择改进的朴素贝叶斯算法作为Stacking的元分类器。朴素贝叶斯算法能够充分利用特征属性与预测信息之间的先验信息，但是朴素贝叶斯的属性独立性假设限制了其使用范围。因此本文通过属性值加权，让每个属性的不同属性值计算不同的权值，使改进的贝叶斯算法削弱独立性假设的条件，可以更好地应用于离散属性分类问题。

1 Stacking集成框架

传统Stacked generalization集成框架于1992年由Wolpert提出[10]。本文为了避免交叉学习导致预测结果出现偏差，在传统Stacking框架的基础上给每个训练集内部嵌套使用5折交叉验证。新训练集和测试集的具体构建过程如图1所示。

图1 新训练集和测试集构建示意图

1.1 元分类器训练集输入构建

在图1中，将原始数据分割为训练集Training和测试集Testing后，对Training做5折划分后，分别表示为{T1,T2,…,T5}。依次取其中4份为训练集，剩余一份为验证集，且每次训练时再将训练集5折划分，表示为{TT1,TT2,TT3,TT4,TT5}，这样每个基分类器对每折数据进行训练都会在内部也交叉训练，以保证每个分类器性能最优。

基分类器分别用{clf1,clf2,…,clfn}表示，n个基分类器经过5×5嵌套交叉验证后得到n组基分类器模型Mji，表示第j个基分类器在第i折数据上得到的模型，其中，j∈{1,2,…,n}，i∈{1,2,…,5}。以clf1为例，5折交叉验证得到5个模型{M11,M12,…,M15}，分别对相应的验证集Ti，i∈{5,4,…,1}做预测，得到预测结果{R5,R4,R3,R2,R1}。将上述预测结果在竖直方向做stack拼接操作后作为次级分类器训练集的第一个特征“新特征1”。重复该训练过程则可得到所有训练集的新特征属性，并与原始训练集Training的类标签Y(按照原始顺序)组合为新训练集，记作：Training_new。

1.2 元分类器测试集输入构建

对于n组基分类模型Mji，以clf1算法在5折数据上训练得到的5个基模型为例，每个模型对Testing做预测得到5组预测结果，对其求平均得到新测试集的第一个属性特征clf1_test，并与新训练集第一个特征“新特征1”相对应。对每一组重复上述步骤即可得到所有测试集的新特征属性，记作：Testing_new。

2 属性值加权贝叶斯元分类器

每个基分类器对应生成一列新特征且属性值取值就是分类类别标签，是离散属性。各基分类器生成的新特征之间、新特征和类别之间都有较强的相关性，因此如何利用相关性产生的先验知识提高模型的预测能力是选择元分类器的重要参考依据。

2.1 算法原理

朴素贝叶斯算法就是利用了贝叶斯公式能根据先验概率推导出后验概率这一特性所提出的，将网络拓扑结构与概率论知识结合，有丰富的概率表达能力。其数学表达式为：

c(x)=arg maxP(c)P(a1,a2,…,am|c)=

(1)

式中：ai表示第i个属性Ai的属性值；P(c)表示先验概率。先验概率P(c)的计算较为容易，但是P(ai|c)由于无法获得可靠的估计，计算并不容易。P(c)的计算如式(2)所示，P(ai|c)的计算如式(3)所示。

(2)

(3)

研究表明，属性加权是削弱朴素贝叶斯算法属性独立性假设的主要改进方向之一[11-12]。为每一个属性变量给定一个权值，然后在加权之后的数据上训练朴素贝叶斯分类器，该方法可以用下式表示:

(4)

式中：m表示属性的个数；Wi表示第i个属性的权重。

由于传统的属性加权方法有一个缺点，如文献[13-14]提出了CFSAWNB、DYAWNB、KLMAWNB等基于过滤法的属性加权方法，文献[15-16]提出了DEAWNB、WANBIANB等基于包装法的属性加权方法都仅仅考虑属性权值，并没有考虑属性值这个深层次因素。针对这一问题，假设每个属性值的重要性可以分解，并且有高度预测性的值与类别有强相关性，与其他属性值不应该相关。根据这些假设，通过计算属性值-类别的相关性、属性值-属性值的冗余性，从而提出一种基于属性值加权的贝叶斯分类算法(Attribute Value Weight Naive Bayes,AVWNB)作为本文中Stacking集成框架的元分类器。

2.2 属性值加权贝叶斯分类算法

m个属性表示为A1，A2，…，Am，s个实例类别表示为c1,c2,…,cs，权值和属性值分别用W和a表示。那么属性加权和属性值加权的权值矩阵可由图2表示。因此属性值加权朴素贝叶斯算法可以用下式分类测试实例x：

(5)

式中：Wi,aj表示第i个特征属性的属性值为aj的权值，是一个正连续值，其取值范围是0到1，代表了属性值aj的重要性。

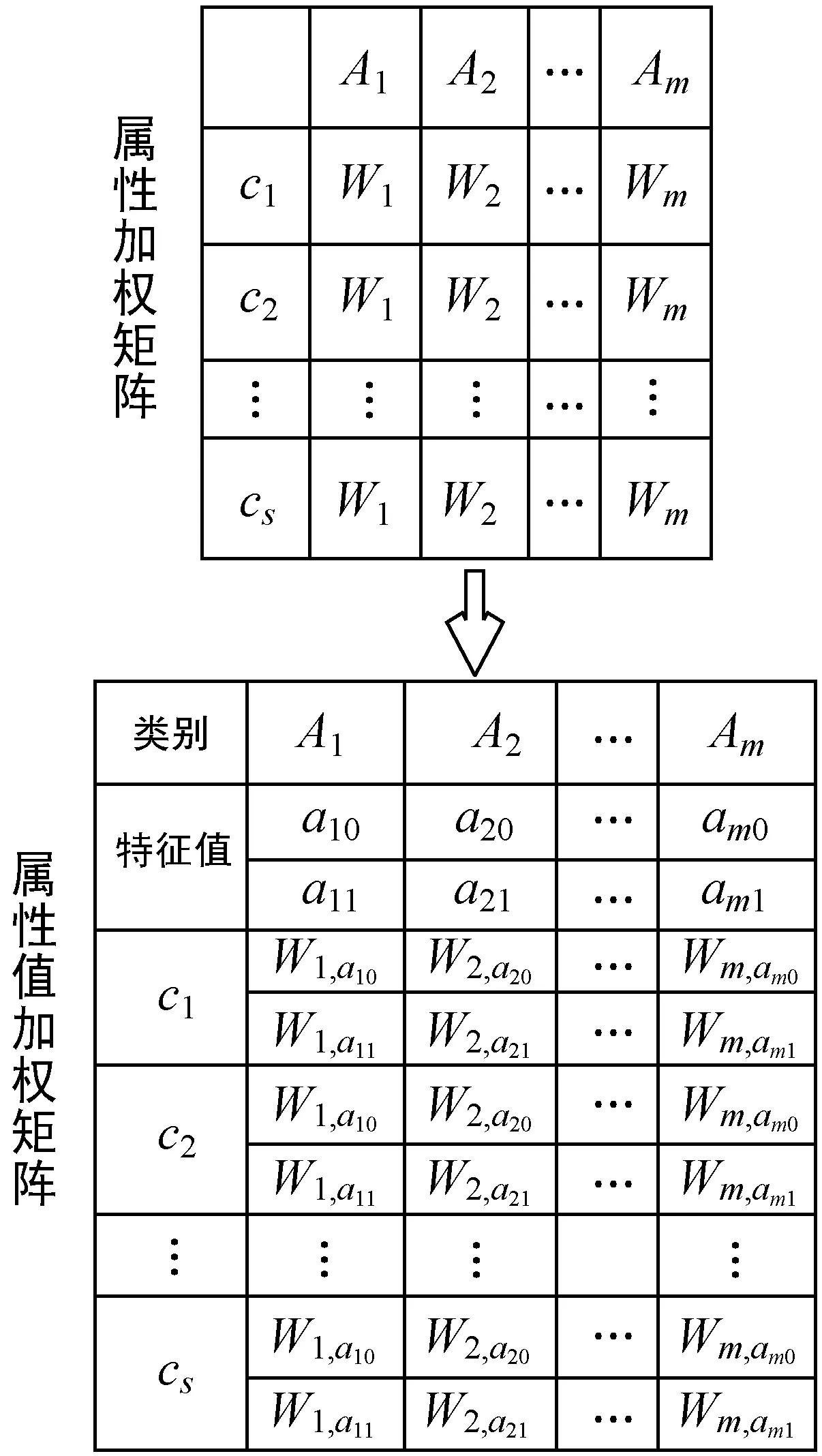
图2 属性加权与属性值加权矩阵

对于属性值权值的计算，认为一个属性值权值的大小取决于其重要性，对最终决策的结果影响大，则权重值就越大。所以一个具有较大权值的属性值ai与所属类别c有较强的相关性，记作N(ai,c)，而与其他属性值aj有很小或者没有冗余性记作N(ai,aj)。属性值ai的权值Wi,ai由式(6)计算，将每个属性值的权重定义为属性值-类别相关性和属性值-属性值平均冗余性的差值。

(6)

式中：加入Sigmoid函数是为了将权值限定在[0,1]区间内，α和β为相关性系数和冗余性系数，经过大量实验验证α取值为0.9～1.0，β为1/m时分类效果最好。

式(6)中N(ai,c)和N(ai,aj)可根据信息熵求解方法计算，信息熵度量广泛应用于计算每一对随机离散变量之间的相关性，将式(7)、式(8)代入式(6)即可求得属性值权值。同时，充分考虑属性值权值对预测结果的影响，将权值Wi,ai代入式(3)中替代λ进行条件概率平滑处理。

(7)

(8)

算法1AVWNB-Stacking算法

输入：训练集Training，测试集Testing。

输出：测试实例类别。

Step1使用基分类器对预处理后的原始数据进行交叉验证训练和预测，得到新训练集Training_new和测试集Testing_new。

Step2对每个属性值ai由式(7)计算与类c的相关性N(ai,c)，对每一对ai和aj计算由式(8)弱依赖性N(ai,aj)。

Step3根据式(6)计算每个属性值αi的权值Wi,ai，基于加权实例数据构建朴素贝叶斯分类器。

Step4按式(5)计算测试实例类别并返回。

3 实验与结果分析

信用评估是一个典型的分类问题，也一直是银行和金融机构评估是否批准贷款申请的关键。具有一般分类数据所有的特性，可以使用信用评估相关数据来验证本文算法的有效性。本文选用的两个数据集信息如表1所示，来自公共数据集uci和数据挖掘竞赛平台Kaggle，下载地址为：https://archive.ics.uci.edu/ml和https://www.kaggle.com。文中使用算法是基于scikit-learn和Python3.6完成的。

表1 数据集信息

3.1 评价指标

由于分类任务数据普遍存在类别不平衡现象，且第二类错误(cost-II)的损失往往比第一类错误(cost-I)所造成的损失更大，所以仅以准确率(Accuracy)作为模型的性能评价指标并不能客观地评价模型的综合性能。因此，本文评价模型的指标还将参考F1值、Recall和AUC值。F1值由式(9)计算，其中precision和recall分别是模型的查准率和查全率。它是查准率和查全率的调和平均数，最大为1，最小为0，取值越大表示模型分类性能越好。

(9)

3.2 结果分析

由于基模型学习能力越强，差异性越大，Stacking集成模型的效果就会越好。因此选择基分类器时，首先选择集成分类器RF、GBDT和LGBM，其次为了增加差异性，选择信用评估中效果较好的单一分类器LR和SVM。同时，为了验证AVMNB-Stacking算法的有效性，第一组实验与基分类器建立的模型、其他集成分类算法(Adaboost和XGBoost)建立的模型比较，其中RF基于bagging思想，GBDT、LGBM、Adaboost和XGBoost基于boosting思想；另一组实验与NB、LR、SVM和RF作为元分类器构建的NB-Stacking、LR-Stacking、SVM-Stacking、RF-Stacking集成算法和文献[17]建立的Stacking模型做比较，实验结果见表2至表5(注：由于数据量过大，表3中SVM模型并未在②数据集上得到数据)。

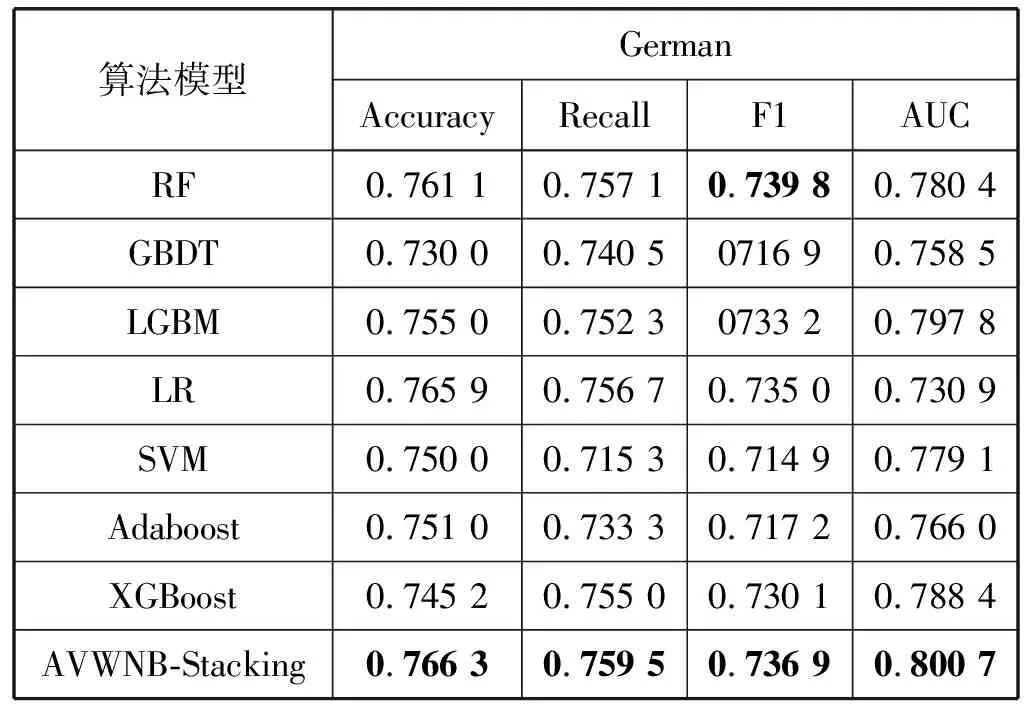
表2 基分类算法和其他集成分类算法与AVWNB-Stacking 算法在German数据集上比较

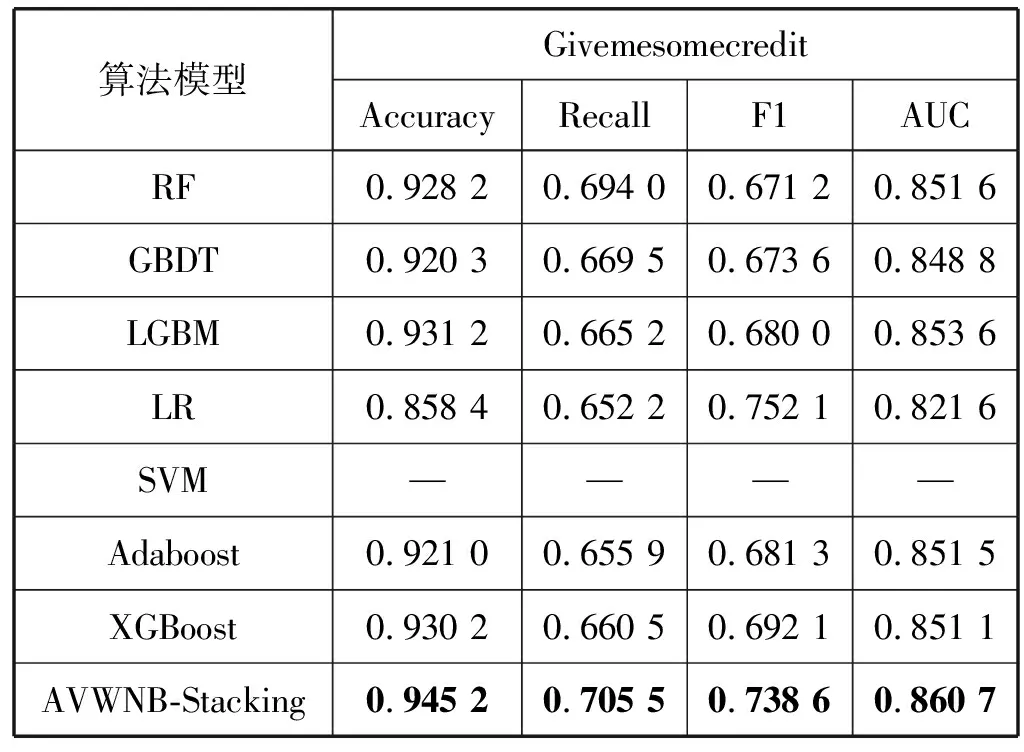
表3 基分类算法和其他集成分类算法与AVWNB-Stacking 算法在Givemesomecredit数据集上比较

可以看出，在基分类算法与其他集成分类算法的实验结果中，RF在①数据集上整体表现最好，LGBM在②数据集上整体表现最好。在①数据集上，Accuracy、Recall和AUC三个指标上AVMNB-Stacking算法都得到了最高的成绩，相比与其他算法，这三个指标平均提高了2.0%、2.1%和3.9%，在②数据集上，AVMNB-Stacking的四个指标都是最高，且提升幅度较大，相比于其他算法，四个指标平均提高：3.4%、5.9%、6.9%和1.7%。

在表4和表5中，①数据集上，AVMNB-Stacking的Accuracy和F1指标没有明显提升，但是Recall和AUC指标提升幅度较大。在②数据集上，文献[17]在Accuracy指标上与本文算法基本持平达到94.38%，这可能是因为文献[17]在改进时主要关注准确率指标，但AVMNB-Stacking的AUC指标提升比较明显，相较于其他Stacking算法平均提高了11.2%。总体上，AVMNB-Stacking算法在两个数据集上都取得了不俗的效果，不仅提高了准确率Accuracy，而且还提高了Recall、F1和AUC，这对于识别“坏客户”是至关重要的。并且在②数据集上的平均提升幅度要比在①数据集上大，主要原因是两数据集数据量差异较大，这是影响Stacking算法效果的关键因素之一。此外，通过实验结果还能发现，尽管LR模型和RF模型没有在各指标上取得最好的分数，但是综合来看仍然是信用评估模型的候选项；也从侧面佐证了当前LR和RF模型频繁出现在信用评估领域不无道理，且LR算法不论是单独建模还是作为Stacking的元分类器，都有稳定、优异的表现；而RF算法单独建模型表现良好，但作为Stacking的元分类器时模型性能不升反降，因此RF算法不适合作为元分类器。

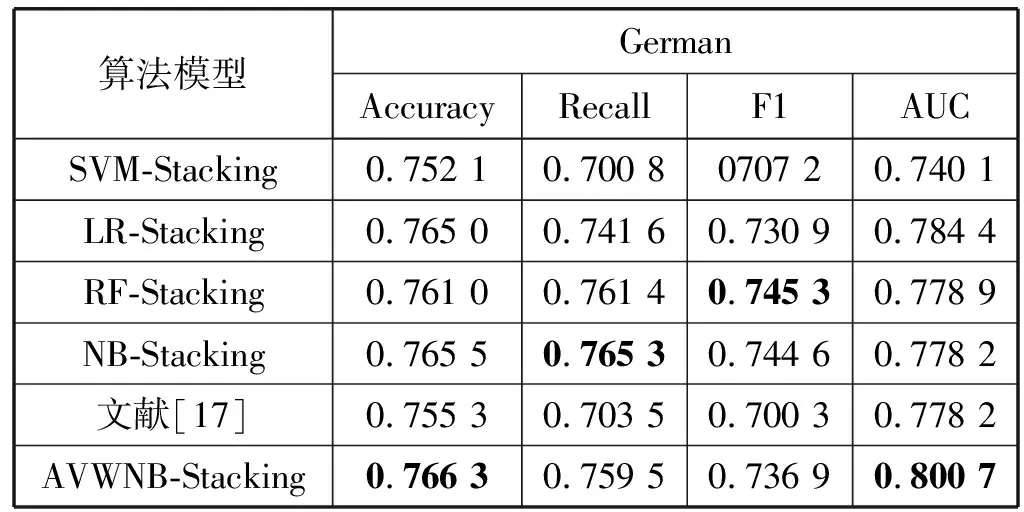
表4 不同Stacking算法在German数据集上比较

表5 不同Stacking算法在Givemesomecredit数据集上比较

K-S曲线是TPR(真阳率)曲线与FPR(假阳率)曲线的差值曲线，用来度量阳性与阴性分类的区分程度。K-S曲线的最高点(最大值)定义为KS值，KS值越大，模型的区分度越好，是信用评估领域专有的模型评价指标。信用评估属于风险模型的一种，应当遵循“宁缺毋滥”的原则，更在意将高风险样例和低风险样例区分出来。因此，相比于二分类问题中常见的ROC曲线或者PR曲线，K-S曲线更适合于评价信用评分模型。选用在分类指标上表现较好的算法进行KS值对比分析，对应曲线如图3和图4所示。

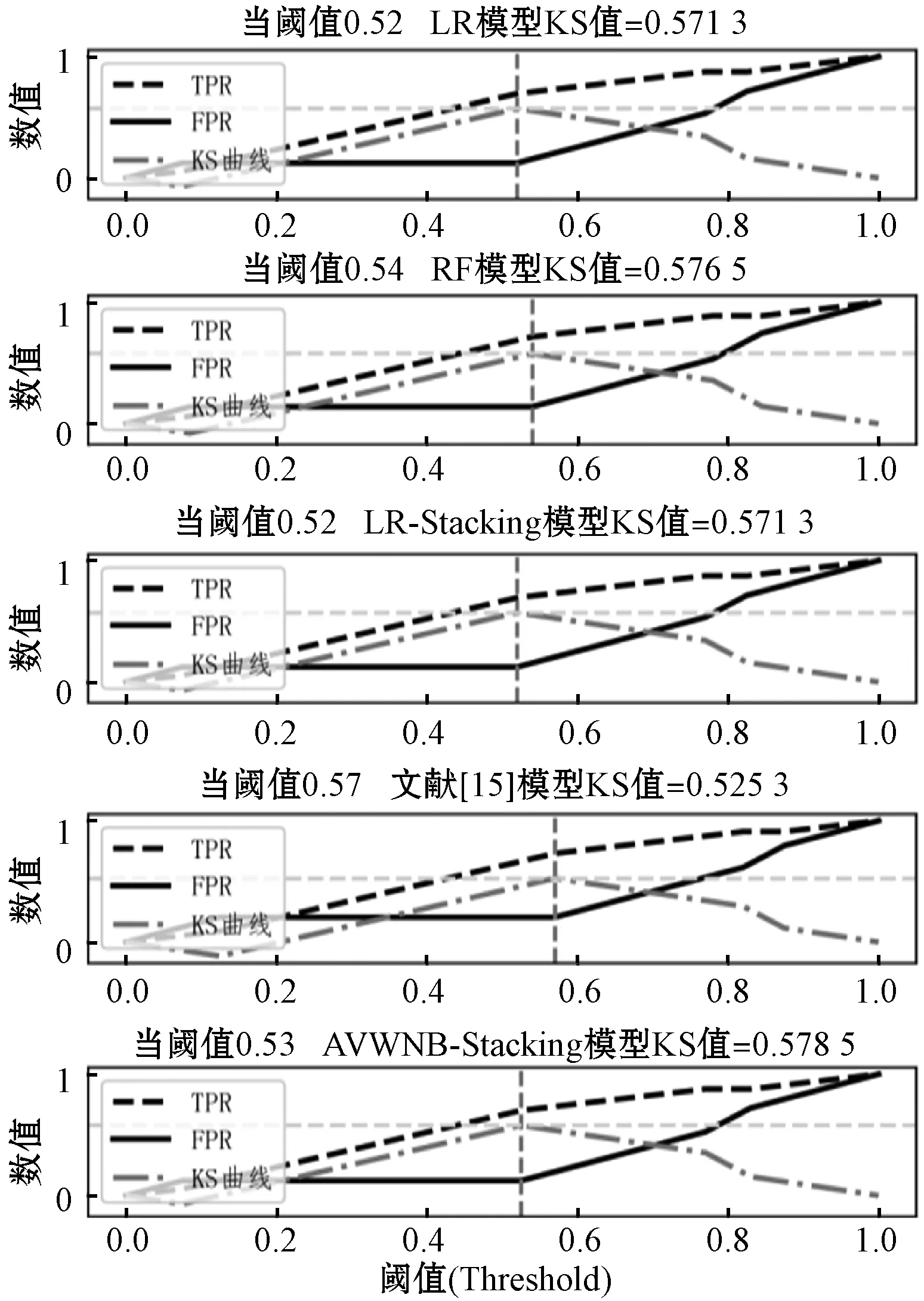
图3 German数据集上K-S曲线

图4 Givemesomecredit数据集上K-S曲线

在①数据集上，LR、RF和AVWNB-Stacking算法的KS值基本相同，都约为0.57，文献[15]较低，KS值只有0.525 3；在②数据集上AVWNB-Stacking算法的KS值要比第二高的XGBoost提升约4.9%。对比两幅图发现，整体上各算法在②上KS值比在①上大，本文的AVWNB-Stacking算法比其他Stacking算法对KS值的提升也比在①数据集上明显，这与前面的结论一致，Stacking算法对数据量大的任务提升效果明显。

4 结 语

本文根据Stacking算法新特征与预测结果之间的强相关性，提出一种基于属性值加权朴素贝叶斯的Stacking集成分类算法，其不仅能够凭借NB算法的特性利用属性的先验知识，还通过属性值加权削弱了NB对属性独立假设条件的影响。在信用评估应用场景下，与传统信用评估算法和其他Stacking算法相比，AVWNB-Stacking算法确实能提高模型准确率、召回率、KS值等各方面的预测效果，也发现AVWNB-Stacking算法对数据量大的任务提升效果比较明显。接下来将进一步研究基分类器数量和实例类别数量对AVWNB-Stacking算法的影响。