基于双流结构的异常行为检测模型

王梓舟 周新志 严 华

(四川大学电子信息学院 四川 成都 610065)

0 引 言

监控系统提供着不间断的监控视频，如此庞大的视频数据使用人工进行处理是效率低下并且困难的。所以自动的视频异常行为检测在近几年越来越多地得到学术界和工业界的关注。

在早期的工作中，研究人员通常使用人工设计特征来表征人体或者人群的行为。Laptev[1]提出了时空兴趣点的方法，其实质是将Harris角点从二维拓展到了三维。Mabrouk等[2]在时空兴趣点的基础上融合光流特征提出DiMOLIF描述子用以检测视频中的暴力行为。Mehran等[3]提出了社会力模型用以检测群体的异常行为。Zheng等[4]使用基于轨迹特征方法检测全局的异常行为。Wang等[5]使用基于光流特征的协方差矩阵进行异常行为的检测。这类方法所使用的特征通常需要经过提前的设计，且检测精确度仍需提高。

随着卷积神经网络的兴起，研究者也将其应用在视频异常行为检测问题上。人工特征由此转向深度网络特征。由于异常行为数据集规模较小，比较难以训练一个复杂的网络，部分工作尝试直接使用经典的深度网络结构解决问题，如Sabokrou等[6]利用在ImageNet上预训练好的AlexNet网络,而AlexNet并非专门针对异常行为问题而设计，所以还存在一定的局限性。另一种思路则是采用结构简单的网络进行训练，如Sun等[7]设计了一种两层的卷积网络提取输入图像特征，再利用OC-SVM(One-class SVM)对特征进行分类。

还有一种针对数据集规模较小问题的常见方法为自编码器(Auto-Encoder，AE)网络。Hasan等[8]使用二维Conv-AE的重建误差来判断异常行为的发生与否。Ribeiro等[9]尝试在2D AE中融合光流以及图像边缘特征。2D AE由于维度上的局限性，并不能很好地获得时域上的信息。为了更好地利用视频时域信息，Chong等[10]、Wang等[11]使用加入Conv-LSTM层的二维卷积AE，LSTM层的加入能够改善2D AE对时域特征提取的性能。Zhao等[12]提出了一种3D AE网络结构用以检测人群和交通中的异常行为。Yan等[13]尝试在2D AE中使用传统光流特征作为输入。取得了一定的进展，但仍有发展空间。此外，Ravanbakhsh等[14]也初步尝试在异常行为问题上使用GAN网络，并在特定数据集取得了不错的成效。

为进一步解决视频时域信息获取和利用的问题，本文设计一种双流网络结构，分别为网络分支以及时域分支。网络分支为3D自编码器，负责提取输入视频的时空特征；时域分支负责对输入视频的光流特征进行处理，提供额外运动信息，并使用改进的策略更好地与网络分支的重建结果进行融合。最终使用融合后的重建结果计算重建误差作为异常行为判断的依据。

此外，目前大部分工作所使用的像素级别评价指标来自Mahadevan等[15]的工作，该像素指标还存在一定的不足。针对这个情况，本文提出一种改进的像素指标。

1 整体框架

1.1 整体流程

整个模型的流程如图1所示。包含有两个分支：网络分支和时域分支。网络分支使用一个3D自编码器，提取连续视频帧的时空域特征，并重建输入，由于自编码器仅使用正常样本进行训练，理论上对异常区域具有更高的重建误差。时域分支得到具有背景的光流结果。最终将两个分支的结果融合得到模型的最终输出，计算最终的重建误差，得到规律性得分并判断是否发生异常。

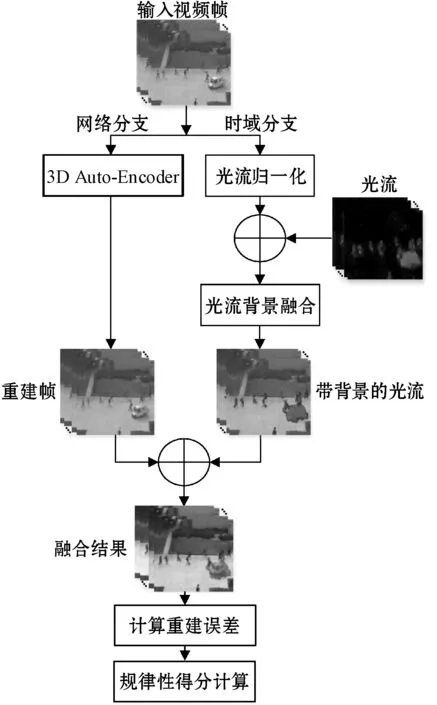
图1 模型整体流程

1.2 3D自编码结构

网络分支使用一个3D自编码器，输入为连续N帧灰度视频图片堆叠形成的一个视频块。由于训练一个深度网络需要大量的训练数据。异常行为检测数据集中的训练样本数量通常都不够充足。受Zhao等[12]的启发，我们在其网络的基础上进行了调整。编码层和解码层改为3层，并更改了3层及后续层的通道数，去掉了额外的网络分支结构。其余参数与原文保持一致。网络结构如图2所示。

图2 网络分支结构

1.3 时域分支

时域分支主要利用经典的光流特征。通过计算连续两帧中对应像素点在x、y方向上的位移值，可得到两个大小与原图片相等的二维浮点值矩阵，每一点的值表征了该点在这两帧中的运动情况，值越大，代表运动幅度越大。可看作是一种时域特征，包含了丰富的运动信息。为了能将光流特征更好地应用到自编码器的方法中，还对其设计进行了如下的处理。

1.3.1绝对值处理

考虑到大部分情况下，物体正、反的运动方向并不作为异常行为判定的条件，而光流特征中，正方向运动的像素点具有正值，反之为负。为排除数值正负带来的影响，保留单纯的运动幅值信息，本文对视频中每一帧的x、y两个方向的光流结果都进行了绝对值处理，再按照式(1)将其归一化到[0,255]区间。

(1)

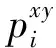
在分别得到x、y方向的结果后，将两者相加，为了防止像素点值超过255。再次对结果使用式(1)进行归一化。

1.3.2背景融合处理

光流帧的背景是黑色的。将这样的光流帧与原视频帧计算重建误差时，会引入额外的偏差，对结果造成负面影响。所以在融合光流和网络重建结果之前，先对光流帧进行背景融合，计算公式为式(2)，得到带背景的光流帧(Optical Flow with Background,OFB)。

令It为视频序列中第t帧，It+1为视频序列中第t+1帧，通过它们计算得到的光流帧为dt，与It对应，那么：

(2)

式中：x、y分别表示像素点在二维光流中的横纵坐标；n是设定的阈值。OFBt是进行了背景融合的第t帧光流帧，为二维矩阵。

图3是光流帧以及融合背景的光流帧OFB的结果。左边第一列为原视频中的帧，第二列为归一化后的光流帧，第三列为融合背景的OFB结果。最后将连续的T帧OFB堆叠为一个体，称为OFBC(OFB Cubic)。与网络分支的重建结果进行融合。

(a) UCSD Ped1数据集

(b) UCSD Ped2数据集

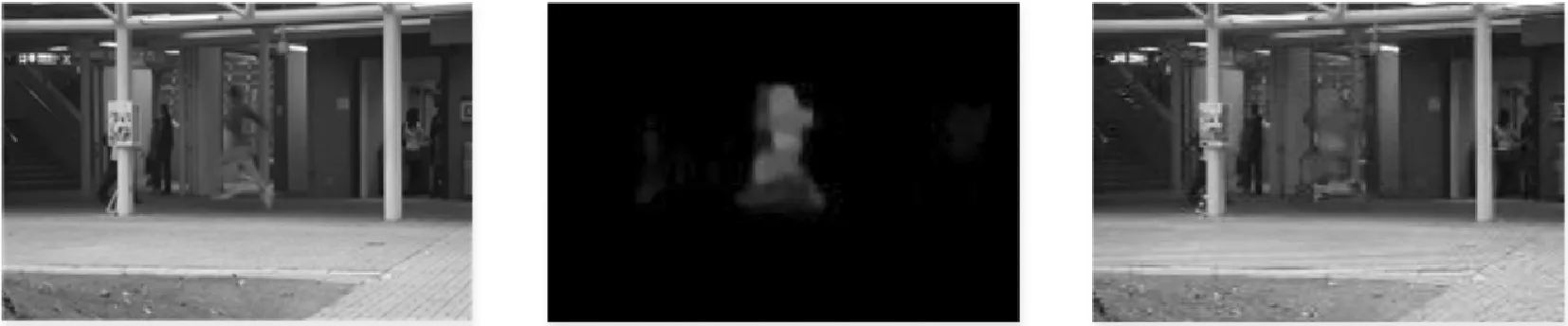
(c) Avenue数据集图3 三个数据集光流帧和OFB的结果

1.4 规律性得分计算

在模型训练完成后，可以得到每一组输入堆叠视频帧的重建结果，按照一定的比例融合网络分支的重建结果和时域分支结果。模型的重建误差由式(3)计算。

(3)

式中：e(t)是第t帧的重建误差；I(t)是输入视频中第t帧；fw是3D自编码器训练得到的权重函数；OFBC是堆叠的OFB帧；a、b是取值范围属于[0,1]的融合因子，两者之和为1，其大小表征了网络分支结果和时域分支结果在最终结果中的影响。

在得到重建误差之后，规律性得分Sr(t)可以表示为：

Sr(t)=1-Sa(t)

(4)

(5)

式中：Sa(t)是视频序列中第t帧的规范化异常得分；min(e(t))和max(e(t))分别代表整个视频序列中最小和最大的重建误差e(t)值。

2 实 验

2.1 数据集

本文在三个经典的异常行为检测数据集上评估本文的方法：Avenue、UCSD Ped1、Ped2。

UCSD数据集[15]包含两个子集Ped1和Ped2，分别对应两个不同的场景。训练视频仅包含正常行为，每个测试视频中至少有一个异常行为。Avenue[16]所有的训练视频短片仅包含正常行为——行人正常行走，而每个测试视频中包括奔跑、抛掷、闲逛等异常行为。

2.2 模型的训练

网络分支的输入为连续16帧堆叠形成的视频块，采用朝后堆叠的方式。对于在堆叠过程中，超出最大帧编号的帧，本文使用视频序列的最后一帧替代。网络以最小化重建误差为训练方向。Batch Size设置为8。

针对UCSD数据集，本文使用Ped1和Ped2的训练数据共同训练一个网络；针对Avenue，本文仅使用了Avenue的训练数据来训练网络。

时域分支只需要输入光流结果，不需要额外的训练。本文使用Liu[17]提供的源码，在MATLAB中计算光流，所有参数均设定为源码中的默认值。OFBC同样采用朝后堆叠的形式，与原始视频帧的堆叠相同。

2.3 分支结果的融合

1.4节中，融合因子a、b的大小无法预先确定，不同的组合会产生不同的结果。在实验中通过枚举的方式搜寻效果最好的组合。在[0,1]区间，a按照步长0.05从0逐渐增加到1，b等于1-a。

2.4 结果和分析

本文从定性和定量两个角度进行评估。定性分析主要通过计算重建误差图来展示异常行为检测的效果。定量分析则通过使用不同的阈值求得多组对应的真阳性率(True Positive Rate,TPR)和假阳性率(False Positive Rate,FPR)，绘制ROC曲线，计算曲线下面积(Area Under Curve,AUC)以及等误差率(Equal Error Rate,EER)。AUC越接近1，EER越接近0，代表效果越好。

2.4.1重建误差结果分析

图4中展示了在三个数据集上，2D AE、网络分支、双分支融合结果的重建误差对比，重建误差使用灰度图进行展示。为了使结果具有可比性，2D AE使用的与网络分支完全相同的输入以及相同的网络结构——仅将网络分支3D AE中的卷积操作、池化操作从三维更改为二维。图中左边一列是原始帧，包含至少一个异常行为，由实线框标记,正常行为由虚线框标记，第二列是2D AE的重建误差，第三列展示的是网络分支的重建误差，最后一列展示的是双分支融合结果的重建误差。颜色越暗代表此处重建误差越低，而越亮则代表重建误差越高。异常行为区域重建误差越大，正常行为区域重建误差越小代表检测效果越好。

(a) UCSD Ped1数据集

(b) UCSD Ped2数据集

(c) Avenue数据集图4 重建误差结果对比

从图4中前三列结果可以看到，无论是正常行为还是异常行为，2D AE都具有较大的重建误差，在图4第一、第二行中尤其明显。这表明二维操作并不能很好地对视频中的正常和异常行为进行区分。一个可能的原因是，二维卷积操作难以获取时域上的信息，输入视频块中的时域信息反而影响了2D AE提取物体空域特征的能力，导致行人等难以被重建。相比于2D AE，虽然3D AE对异常行为的重建误差有所减小，但正常行为的重建误差也得到了有效的降低。

时域分支所采用的OFB能够更突出整个视频中运动幅度相对较大的区域，对正常行为和异常行为在速度指标上进一步区分，达到增加异常行为重建误差的效果；通过在光流结果中引入原始帧背景，一定程度修正自编码器对背景、站立的行人等正常区域的重建结果——减少它们的重建误差。因此能够提高异常区域和正常区域的区分度。在图4中最后一列，展示了双分支融合后与原始视频帧的误差。可以看到相比于前两列的结果，时域分支的加入确实进一步提升了区分度。

2.4.2帧级别结果分析

时域分支提取的主要是视频中的时域运动特征。网络分支通过3D卷积操作，能同时获取物体在空域形态上的特征以及部分时域上的运动信息。因此两个分支融合后，时域分支能够向网络分支提供额外的运动信息，而网络分支能够为时域分支提供一定的空域信息，达到两个分支互相补充提升检测效果的目的。

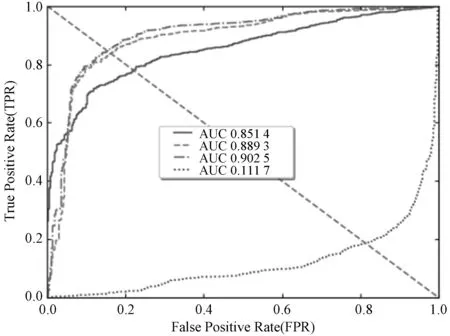
本文分别测算了三个数据集上网络分支的ROC曲线、时域分支的ROC曲线、两个分支融合后的ROC曲线。结果如图5所示。融合的结果(点横线)比网络分支(实线)以及时域分支(短横线)的AUC值都要更高，说明两个分支融合确实产生了互补的效果。另外图5中直接融合普通光流(点线)情况下的曲线下面积AUC结果低于50%。这说明使用OFB的方法在提供运动信息的同时，能够避免像普通光流一样对检测结果产生负面影响。相比于普通光流，使用OFB的时域分支是一种更适合与自编码器结合的方法。

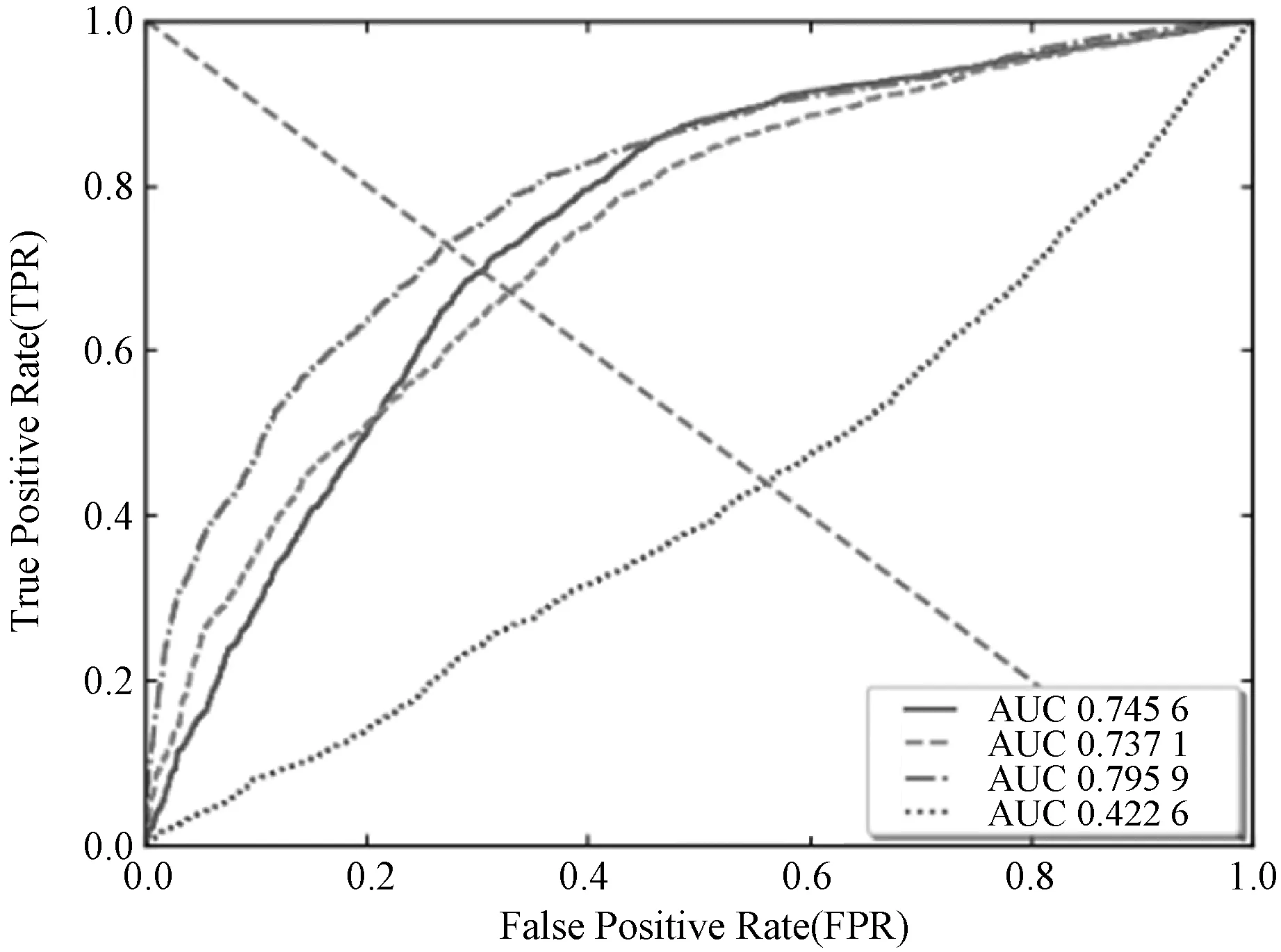
(a) UCSD Ped1

(b) UCSD Ped2

(c) Avenue图5 三个数据集上的ROC曲线结果对比

本文与一些方法在Ped1、Ped2、Avenue上进行了结果的对比，结果展示在表1中。

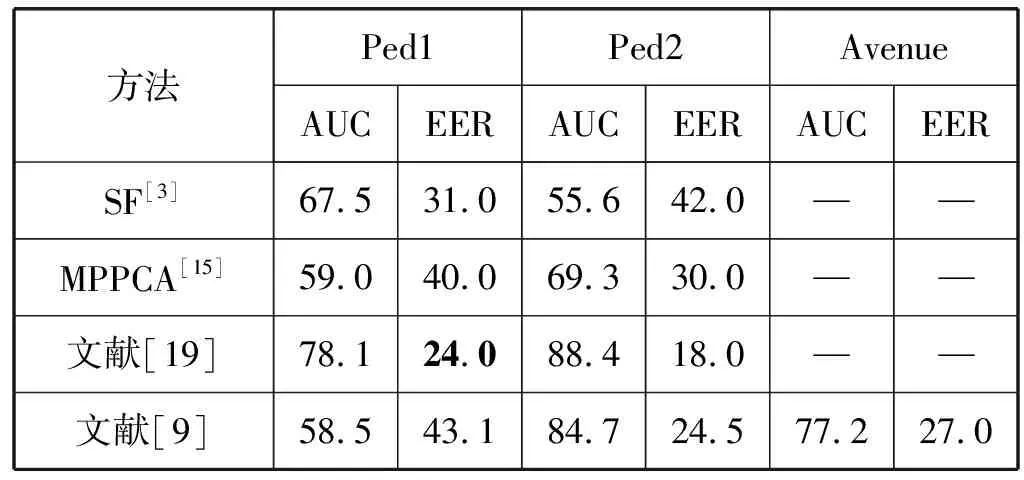
表1 帧级别AUC和EER结果对比(%)

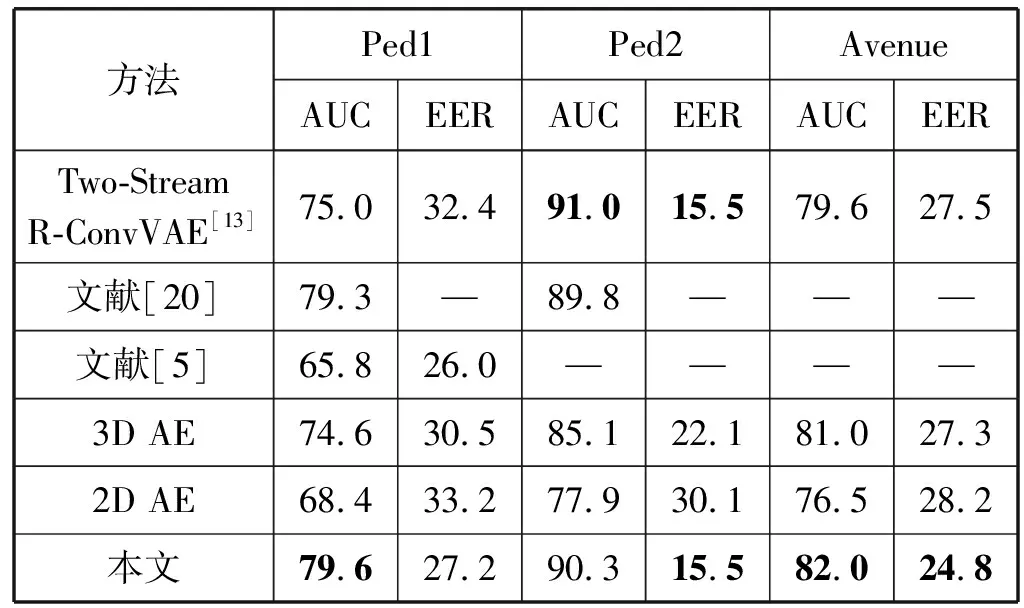
续表1

在Ped1上，本文有最高的AUC；在Ped2中，仅有文献[13]的AUC结果略高于本文，高0.7百分点，EER上本文与其并列为最低，为15.5%。而在Avenue数据集上，本文有最高的AUC 82%以及最低的EER 24.8%。表1中3D AE指只使用网络分支，2D AE则是将网络分支的卷积、池化操作更改为二维，本文方法则是将网络分支与时域分支进行了融合。3D AE分支的结果在三个数据集上都优于2D AE结果，而加入时域分支后，能与网络分支互补，进一步整个提升模型的结果。

2.4.3像素级别结果分析

目前大部分工作的像素级别评价指标按照Mahadevan等[15]所提出的为标准。其定义如下：当40%及以上的异常像素被算法正确标记，则认为当前帧被正确检测为异常。

在这种标准下有两个不足之处：

(1) Mahadevan等提出以40%为判断阈值，但并未说明设置为40%的依据。

(2) 某些情况下算法正确检测出了40%以上的异常区域像素的同时，也误标记了其他正常区域，会简单认定为正确定位出异常(True Positive)，而没有将正常区域被误判纳入考虑。如图6所示，图中异常的小汽车被正确标记，但正常行人也被误标。

图6 异常区域正确标出、正常区域误标的情况

针对这两点，本文提出一种改进的像素级别检测指标。对模型输出结果中所有像素点逐个进行异常与否判断，像素值大于阈值的像素点，判定为异常，小于阈值的则判定为正常。再将结果与Ground Truth进行比较。设置多组阈值，绘制ROC曲线，得到AUC以及EER。AUC越接近1、EER越接近0代表效果越好。

使用改进的指标不再需要经验性地设置40%这样的取值，且即使出现了图6中的情况，被误标的正常像素个数最终会影响ROC曲线结果。

在这种像素指标下，本文在UCSD上的结果如表2所示。由于光流结果具有一定的前景提取能力，所以加入时域分支能够提升整个模型的异常定位能力。从图4最后一列的结果以及表2中的结果均可以看出模型对异常行为具有一定的定位能力。

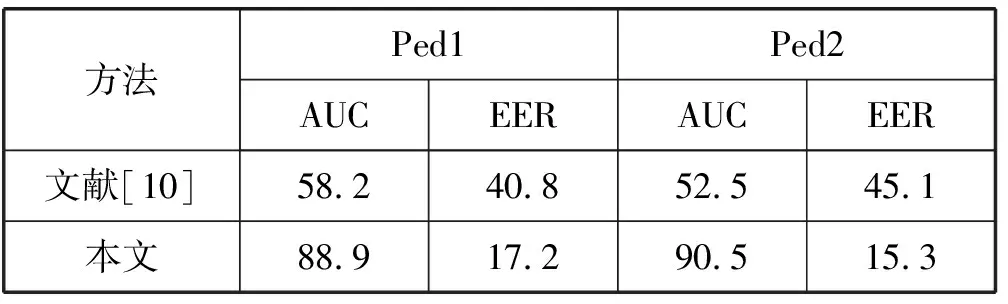
表2 UCSD数据集上的像素级别AUC和EER(%)

3 结 语

为更好地利用视频异常行为检测中视频的时域信息，本文提出一个双流分支网络结构用来提取视频的特征并进行异常行为检测，并从定性和定量的角度进行了对照，证明双分支的网络结构能够更好地利用视频的时域信息，互为补充，提升整体的检测精确度。此外，提出一种改进的像素评价指标，能够一定程度弥补之前像素指标的不足。未来的工作主要是进一步提升模型在各个数据集上帧级别和像素级别的检测精度。同时提升模型的实时性。