基于卷积神经网络的单路PPG信号的连续动脉血压测量算法

李欣悦 葛 慧

(中国航天系统科学与工程研究院 北京 100048)

0 引 言

常见的连续无创动脉血压测量方法有动脉张力测定法、容积补偿法和超声法，但这些方法鲁棒性差且操作较为复杂。脉搏波参数测定法是当前一个重要的研究方向，利用PPG信号特征参数与动脉血压间的关系来建立动脉血压测量模型。该方法可以分为脉搏波传播时间法(Pulse Transit Time,PTT)和脉搏波特征参数法两类。PTT法计算出脉搏波从心脏位置传导至PPG信号测试点的时间差，利用线性回归模型建立PPT与收缩压(Systolic Blood Pressure，SBP)和舒张压(Diastolic Blood Pressure,DBP)的关系[1]。理论表明，PPG和EGG信号与动脉血压间存在着某种关系，因而可利用深度学习技术提取PPG和EGG的特征参数来建立其与动脉血压间的关系[2]。但此方法需要使用电极线采集EGG信号，这会增加设备的复杂度。

脉搏波特征参数法对PPG信号进行特征筛选并通过机器学习算法来建立其与动脉血压间的关系，但是设计良好的特征需要充足的先验知识，因而具有局限性[3]。有研究者提出对PPG信号使用自编码器技术来提取特征，实验结果表明，较人工设计的特征参数，该方法的精确度更高[4]。然而这些对于连续动脉压的预测，EGG信号不是必要的。

近年来，CNN在图像识别、自然语言处理领域被广泛应用，在特征提取上表现优异。VGGNet[5]是一种典型的CNN结构，此算法使用VGGNet来提取每搏血压值所对应的PPG信号特征参数，并将其输入到神经网络的全连接层来预测与动脉血压间的关系。较于先前的方法，此算法优点为：仅使用单路PPG信号，降低了采集设备的复杂度，增强算法鲁棒性；使用CNN提取每搏血压值所对应的PPG信号特征参数，去除了对先验知识的依赖并提高了动脉血压测量值的准确度。

1 基本原理

1.1 卷积神经网络

卷积神经网络[6]是一类包含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一。其具有表征学习能力，能够按其阶层结构对输入信息进行平移不变分类，因此也被称为平移不变人工神经网络[7]。

CNN一般由输入层、隐含层、输出层所构成，输入层可以处理多维数据，隐含层通常由若干卷积层、池化层和全连接层所组成，使用线性整流函数(ReLU)作为激活函数。

对于卷积层可设定一个或多个卷积核，对输入进行卷积操作后,会得到一个或多个特征图，将特征图连接到池化层。池化层将根据设定的步长，对特征图进行下采样,输出更少的数据。如此反复接入卷积层、池化层，能在低层次的特征表示上进一步提取隐藏特征，得到高层次的特征表示。最终将提取的高层次特征表示连接到一层或多层全连接层中进行非线性组合以得到输出，以完成学习目标。典型的CNN结构如图1所示。

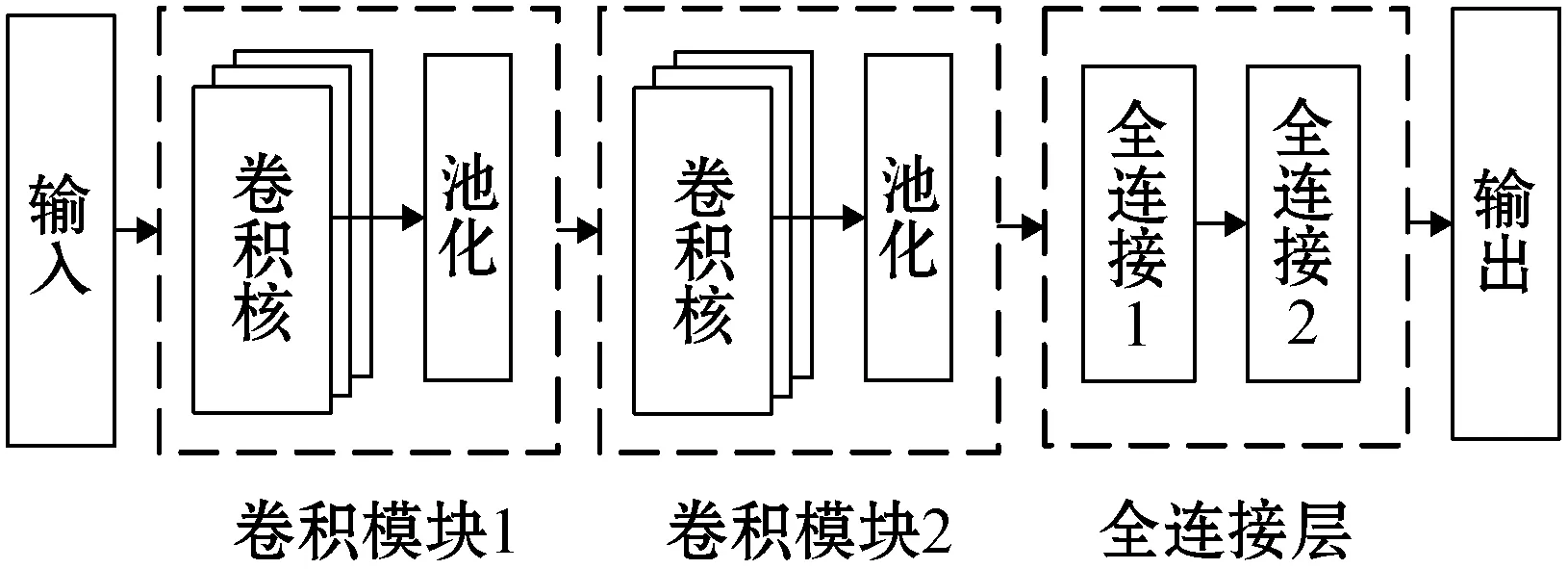
图1 CNN结构图

1.2 批标准化

根据ICS理论，当训练集的样本数据与测试样本集分布不一致时，训练得到的模型无法很好地泛化。在神经网络训练过程中，每一层的输入在经过层内操作之后将不同于输入的信号分布，并且经过前向神经网络的传播，信号分布差异逐渐累积，导致网络难以收敛。

批标准化(Batch Normalization,BN)能有效解决这一问题。BN算法常与批量随机梯度下降算法一同使用，在计算神经网络的前向传播时，对每层每批m个输入数据B={x1,x2,…,xn}做以下处理：

(1)

(2)

式中：μB为输入数据的均值；σB为输入数据的方差；ε为超参数；γ和β是通过模型学习所得；yi表示批标准化后的数据。

1.3 损失函数和评价指标

参数的优化过程依赖损失函数，通常会根据具体的任务来设定损失函数，在训练过程中迭代更新神经网络参数以最小化损失函数，直到其值满足某一阈值。评价指标能评估训练所得的神经网络的泛化能力。

在训练神经网络时，为减少泛化误差，限制模型学习能力，故使用带有参数范数惩罚的损失函数。此算法使用带有L2范数的均方误差(MSE)作为损失函数：

(3)

(4)

将平均误差(ME)、标准差(SE)和相关系数(CC)作为模型评价指标，具体公式如下：

(5)

(6)

(7)

式中：μ是平均误差。

1.4 交叉验证

在机器学习中，一个小规模的测试集意味着平均测试误差估计的统计不确定性，无法只根据模型在小规模测试集的性能来推断其真实性能。为解决这一问题，有学者提出k折交叉验证法，将数据集分成k个不重合的子集，第i个子集作为验证集，其余k-1个子集数据作为训练集，对神经网络进行k次训练和验证。最终，验证误差可估计为k个验证误差的均值。

1.5 整体网络结构

本文所使用的神经网络结构如图2所示，输入是单通道的PGG信号，中间层是VGG-16网络，输出是中心动脉压的SBP和DBP。VGG-16包含13个卷积层(图2中CONV1-64代表第一个包含64个卷积核的卷积层)、5个最大池化层和3个全连接层，卷积核的尺寸均是3，步长为1，最大池化层参数均是2。在每个卷积层和全连接层之后使用BN和ReLU激活函数。

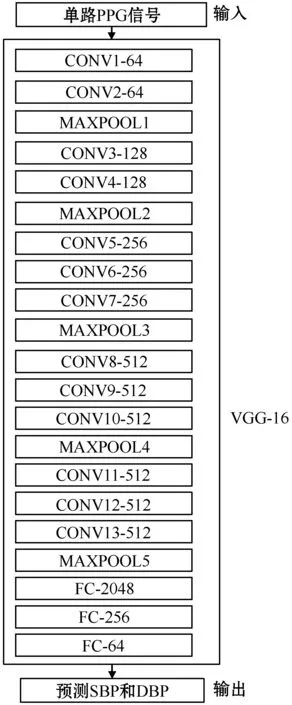
图2 整体网络结构图

2 算法实现

2.1 概 述

本文所设计的动脉压算法实现流程如图3所示。首先对PPG信号进行滤波处理以实现去噪、平滑；对PPG信号进行归一化处理；将PPG信号分割为多个单周期；对每个单周期PPG信号进行插值处理以得到固定长度；将处理完成后的单周期PPG信号及其对应的SBP和DBP输入到神经网络中进行训练，获得动脉压值和PPG数据间的关系。

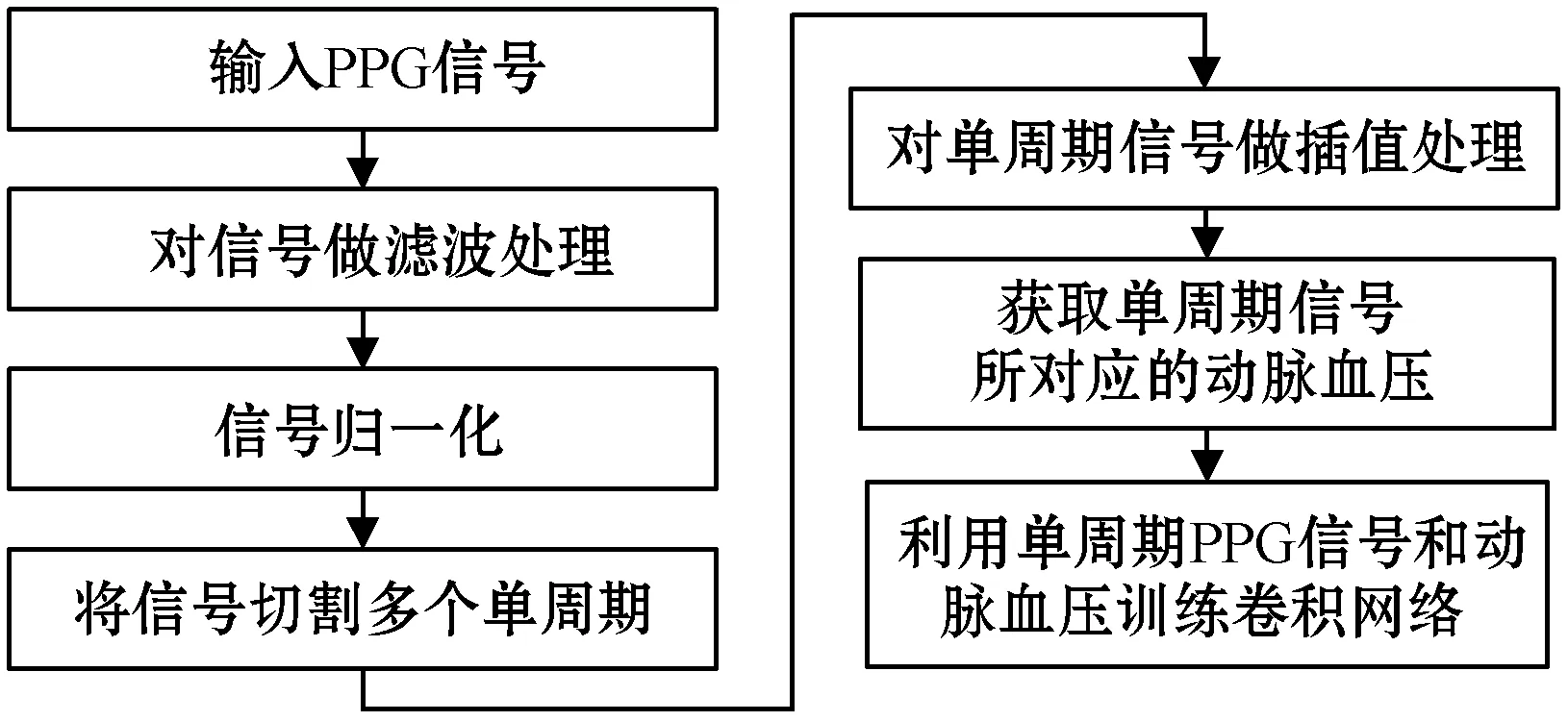
图3 算法实现流程

2.2 数据预处理

从MIMIC数据库中筛选出同时包含PPG信号(f=125 Hz)和动脉血压信号(f=125 Hz)的13个病人数据记录。在测量过程中，由于呼吸、身体抖动会使得PPG信号产生基线漂移，原始PPG信号及其对应的动脉血压信号如图4和图5所示(截取某病人部分数据)。

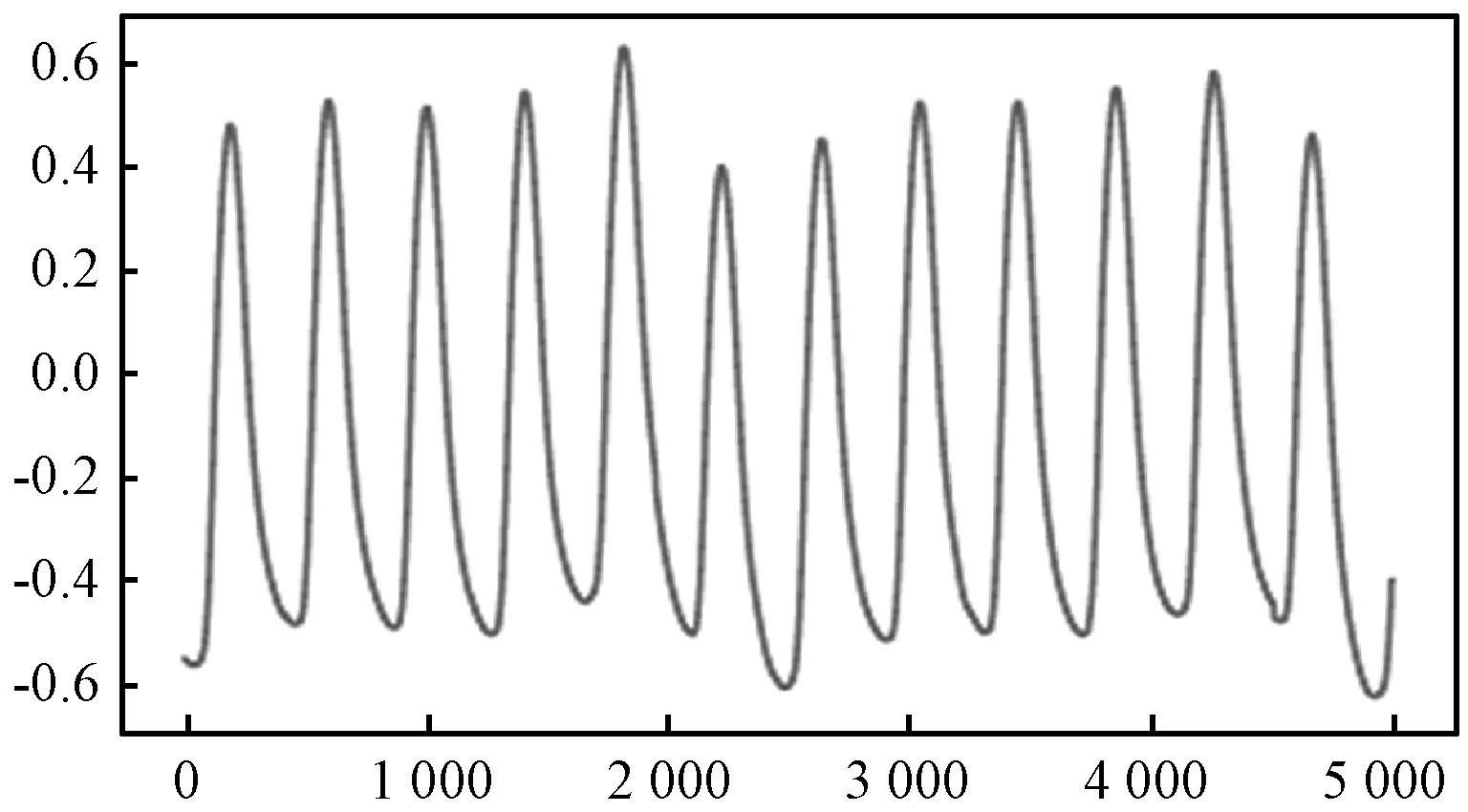
图4 MIMIC数据库中的PPG信号

图5 MIMIC数据库中的ABP信号

因此，在将信号输入到卷积神经网络前，需进行滤波处理来去除原始信号中的噪声。实验中采用二阶巴特沃斯带通滤波器来滤除基线漂移，其由一个二阶巴特沃斯高通滤波器(截止频率为30 Hz)的和一个二阶巴特沃斯低通滤波器(截止频率为0.5 Hz)叠加组成。此外，使用中值滤波对信号进行平滑处理。滤波结果如图6所示。对无噪声干扰的信号做归一化处理，使其分布满足均值为0，方差为1。

图6 经滤波器处理后的PPG信号

2.3 单周期切割

已有研究表明，对PPG信号做二阶微分得到的加速度容积脉搏波(APG)，其波峰值对应单周期信号的起点，如图7所示[7]。因此，利用自适应阈值法来识别APG的波峰进而可以确定单周期PPG信号的起始点。实验中设定阈值为0.6max(APG(n))，其中max(APG(n))表示当前APG信号的最大值，大于此阈值便认为是PPG单周期的起始点。实验结果表明，阈值系数设置为0.6时，能够筛选出APG信号的波峰，进而可确定出单周期PPG起始点。最终可得如图8所示的单周期PPG信号。

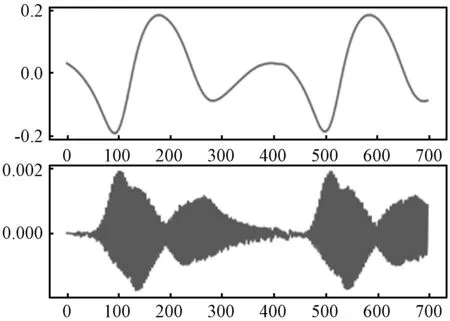
图7 PPG信号及其对应的APG信号

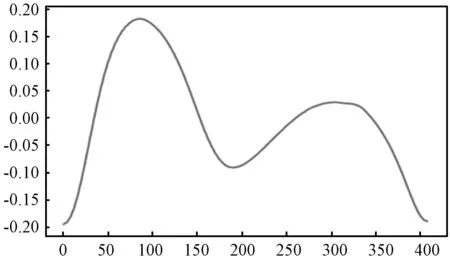
图8 单周期PPG信号

根据切割得到的单周期PPG信号来计算对应周期内动脉血压的最大值和最小值，分别记作SBP和DBP，单位均为mmHg，将SBP∈[80,180]且DBP∈[50,130]所对应的967个PPG单周期信号及其相应的SBP和DBP值作为训练样本，50个单周期及其相应的SBP和DBP值作为测试样本。

2.4 插值方法

插值法利用曲线中若干已知的采样点，通过应用某些特定的函数，在曲线的某些位置上计算对应的函数值，作为该位置曲线的近似值。常见的插值方法有片段插值、线性插值、多项式插值、样条插值等。

由于CNN处理的是定长数据，而单周期切割后的PPG信号数据长度各不相同。实验中采用三次多项式插值法对所得PPG信号进行插值处理，使得单周期PPG信号采样个数均为512。

2.5 训练神经网络

本文提出的神经网络模型包含1个输入层、1个VGG-16网络和1个输出层。输入层用于输入预处理完成后的单周期PPG信号，其特征点的个数为512；VGG-16网络包含13个卷积层(卷积核的尺寸均为3，步长为1)、5个最大池化层(参数均为2)、3个全连接层(神经元个数分别为2 048、512、64)；1个输出层(含2个神经元)，用于输出预估的SBP和DBP。为加快神经网络收敛速度，在各卷积层及全连接层之后加入BN层。实验中采取10折交叉验证法训练并验证神经网络性能，选取带有L2范数的MSE作为优化函数，并利用初始学习率为0.006的Adam优化器来训练神经网络，选用ME、SD及CC作为模型性能的评价指标。

3 实 验

应用10折交叉验证法训练样本集，训练过程误差曲线如图9所示。可以看出，代价函数收敛速度较快，在100轮之后，下降缓慢。模型在测试集上的评价指标如表1所示。SBP的精确度为-0.51±3.23 mmHg，DBP的精确度为-0.05±1.89 mmHg，均满足AAMI所制定的5±8 mmHg的要求[8]。测量的SBP和DBP和真实的SBP和DBP相关性系数值分别为0.988和0.981，表明测量值和真实值之间具有强相关性。

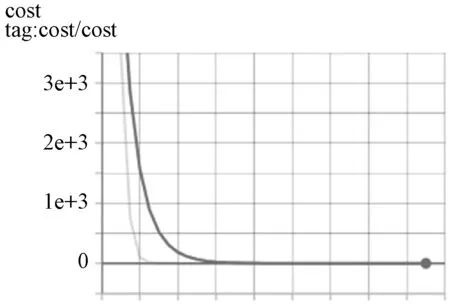
图9 损失函数的变化趋势

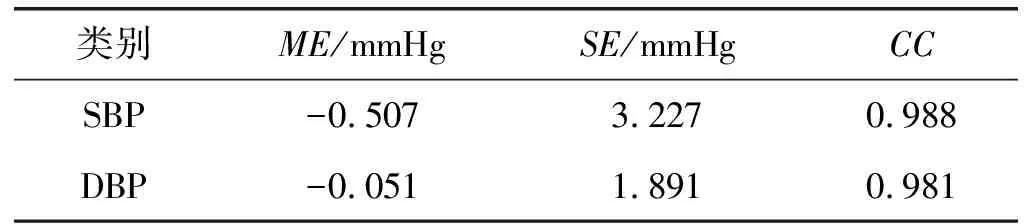
表1 算法在测试集的评价指标

利用Bland-Altman方法[8]对血压算法的准确性进行一致性检验，检验结果如图10和图11所示。横轴表示真实血压值和测量血压值的平均值；纵轴表示真实血压和测量血压的差值。SBP的一致性占比为95%，DBP的一致性占比为95%，可以看出，大多数测试样本满足要求，测量结果较为准确。

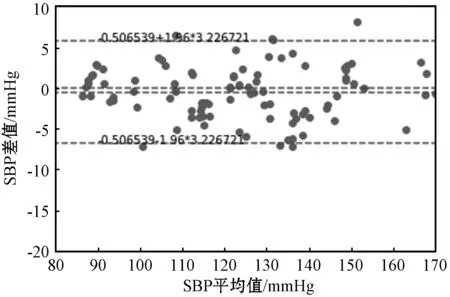
图10 SBP的Bland-Altman图

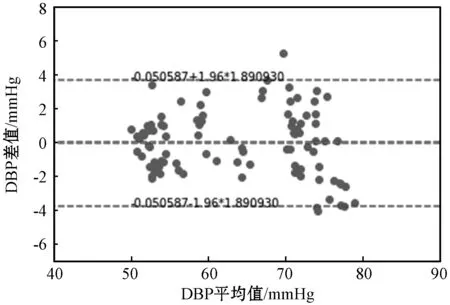
图11 DBP的Bland-Altman图

观察实验结果，在测试样本中，存在个别实验对象的估测血压值和真实血压值有较大的差异。这表明模型的泛化能力有待提升，未来仍需通过扩增样本个数并不断优化模型参数，以进一步提高算法的准确度。

4 结 语

本文算法使用CNN来提取PPG信号的特征值，进而预测其与动脉血压间的关系。实验结果表明，该算法满足AAMI所制定的标准。在CNN中：通过对PPG信号做卷积、池化和批标准化等操作，能提取出表征局部信号的显著特征值；通过多层CNN的处理，最终可以得到PPG信号高层次的特征表示来建立其与动脉压间的关系。

利用本文算法所求得的血压值与实际值间具有较好的一致性，SBP与DBP一致性占比均达到95%以上，且SBP与DBP的精确度分别为-0.51±3.23 mmHg和-0.05±1.89 mmHg，均满足AAMI制定的5±8 mmHg的要求。但仍存在少量测试样本的真实血压值和测量值之间有较大的误差，未来仍需进一步优化模型参数。