无迹卡尔曼滤波算法在污水处理BSM1过程中的应用研究

曾 静 桑耀凯 李 元

(沈阳化工大学信息工程学院 辽宁 沈阳 110142)

0 引 言

污水处理是水循环的重要环节，涉及到复杂的生物和化学反应。污水处理过程(Wastewater Treatment Process,WWTP)是一个典型的非线性系统，其出水水质与环境的可持续性密切相关，通常由环境立法进行管理，在满足环境法规的严格要求的同时，还要求确保工艺安全并将运行成本降至最低。污水入水流量和成分的显著变化导致设计污水处理厂的先进控制和监测方案的复杂性增加。污水处理过程的典型仿真模型BSM1(Benchmark Simulation Model no.1)由活性污泥1号模型(ASMI)和双指数沉淀速度模型组成，作为标准仿真平台广泛应用于污水过程的控制、优化、系统监视及故障诊断等研究中[1-2]。

关于污水处理过程的控制算法有许多研究成果。早期利用比例积分(Proportional-Integral，PI)控制进行污水处理厂营养物去除，PI控制可以达到运行中的稳定性要求，但不能有效处理约束[3]。近年来模型预测控制(Model Predictive Control，MPC)等先进控制方法也引起了人们的广泛关注。英国兰卡斯特的污水处理厂的应用证明了模型预测控制的有效性[4]。Francisco等[5]为BSM1基准仿真模型1号开发了MPC控制器，文献[6-8]考虑了污水处理厂MPC的同步设计和控制问题。Zeng等[9]将经济的MPC算法(Economic Model Predictive Control，EMPC)应用于BSM1，设计考虑终端代价(Terminal Cost)的经济模型预测控制器，并将EMPC性能与常规MPC、PI进行了分析比较，在保证系统稳定性的基础上显著提高了出水质量，同时降低了全局能耗指标。

虽然关于污水处理厂控制系统设计的研究成果很多，但对污水处理厂状态估计的关注相对较少。状态估计是基于输出测量和系统模型重构系统状态的过程。状态估计与污水处理厂的控制和监测密切相关，是污水处理厂运行中的一个重要课题。污水处理中的许多相关状态是不可测量的或受到严重的噪声污染。扩展卡尔曼滤波(Extended Kalman Filter，EKF)曾被应用于BSM1的状态估计[10]。然而EKF滤波器线性化存在局限性,例如对于较强非线性模型需要计算的步长尽可能小。Julier等[11-13]提出了一种新的非线性滤波方案来替代EKF在目标跟踪领域的应用，后来被命名为无迹卡尔曼滤波(Unscented Kalman Filter，UKF)。

基于上述考虑，本文针对污水处理的典型模型BSM1设计了无迹卡尔曼滤波器，并与扩展卡尔曼滤波的状态估计结果进行比较。主要工作包括：(1) 详细地描述EKF和UKF的算法理论及二者的优缺点，并描述无迹卡尔曼滤波的理论依据。(2) 将EKF与UKF在同一噪声下应用于BSM1仿真，将仿真结果进行对比分析，得出二者方案各自的优缺点和最好的估计方案。(3) 在不同天气条件不同噪声大小状况下，对EKF、UKF两种方案在BSM1应用进行比较,分析比较结果。

1 EKF算法描述

扩展卡尔曼滤波算法理论在于对原系统方程和测量方程采取一阶泰勒展开来近似逼近实际系统非线性模型。通过求偏导计算所需的雅可比矩阵确定出当前的系统矩阵F(k)和输出矩阵H(k),为了不失一般性，我们设系统模型的状态方程和输出方程如下：

x(k)=f(x(k-1))+w(k-1)

(1)

z(k)=h(x(k))+v(k)

(2)

式中：f(·)为系统状态方程、h(·)为系统输出方程，二者为非线性函数；x为系统的状态变量；w(k-1)为系统k-1时刻过程噪声；v(k)为系统k时刻测量噪声；z(k)为系统在k时刻测量值。其中噪声均服从零均值的高斯分布。为了确定系统矩阵和输出矩阵，对状态方程和测量方程求偏导，得：

(3)

(4)

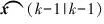
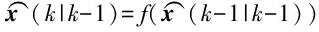
(5)

P(k|k-1)=F(k-1)P(k-1|k-1)FT(k-1)+Q

(6)

式中：P(k-1|k-1)为k-1时刻的误差的协方差矩阵；P(k|k-1)为k-1时刻预测k时刻的误差协方差矩阵；Q为过程噪声的协方差矩阵。测量更新如下：

K(k)=P(k|k-1)HT(k)[HT(k)P(k|k-1)H(k)+R]-1

(7)

(8)

P(k|k)=P(k|k-1)-K(k)H(k)P(k|k-1)

(9)

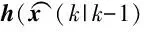
2 UKF滤波算法描述

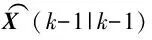
(1) 利用初始估计值，生成初始的L个Sigma点：

(10)

(2) 利用状态方程计算Sigma点的一步预测：

χ(i)(k|k-1)=f(χ(i)(k-1|k-1))

(11)

(3) 对经过非线性传递之后Sigma点加权计算：

(12)

(4) 计算协方差矩阵的一步预测：

(13)

(5) 利用测量方程计算一步Sigma点的测量值：

Z(i)(k|k-1)=h(χ(i)(k|k-1))

(14)

(6) 计算测量值的预测加权求和：

(15)

(7) 计算新息的协方差：

(16)

(8) 计算协方差：

(17)

(9) 计算Kalman增益：

(18)

(10) 更新误差协方差矩阵：

PX(k|k)=PX(k|k-1)-K(k)PzzK(k)T

(19)

(11) 利用新息更新状态，z(k)为当前实测输出：

(20)

3 仿真实验

将上述介绍的UKF算法应用于BSM1模型，并与EKF在不同天气和不同大小噪声条件下的估计性能进行比较分析。BSM1的模型描述详见文献[10，14]。三种不同天气条件数据文件分别为干燥天气数据文件、降雨天的数据文件和暴风雨天的数据文件，详见国际水协会的官网(http://www.benchmarkwwtp.org)。干燥天气包含了两周相同的动态干燥条件数据；雨天数据文件中包含一周的动态干燥条件数据和发生在第二周的一次长降雨事件；暴风雨天的数据文件中包含了一周的动态干燥条件和发生于第二周期间的两次暴风雨事件。生物反应器和理想分离器的初始值通过模拟工厂100天的输入，并在干燥条件下模拟14天计算得到的。由于三种不同天气状况的输入数据前一周是完全相同的，因此仿真直接从第二周开始。在仿真中，假设对整个过程测量进行采样是同步和周期性的，采样周期取15 min，系统的状态变量包括5个反应器及二次沉降池变量(SALK、XBH、XI、XS、XND、XP、XBA、SI、SS、SO、SNO、SNH、SND)见表1，反应器及沉降池可测量变量(SO，SALK，SNH，SNO，COD，CODf，BOD，TSS)见表2。在每组的仿真中，将相同的测量噪声、过程噪声序列和相同的初始值分别应用到EKF、UKF方案上，过程噪声和测量噪声均为有界高斯白噪声。

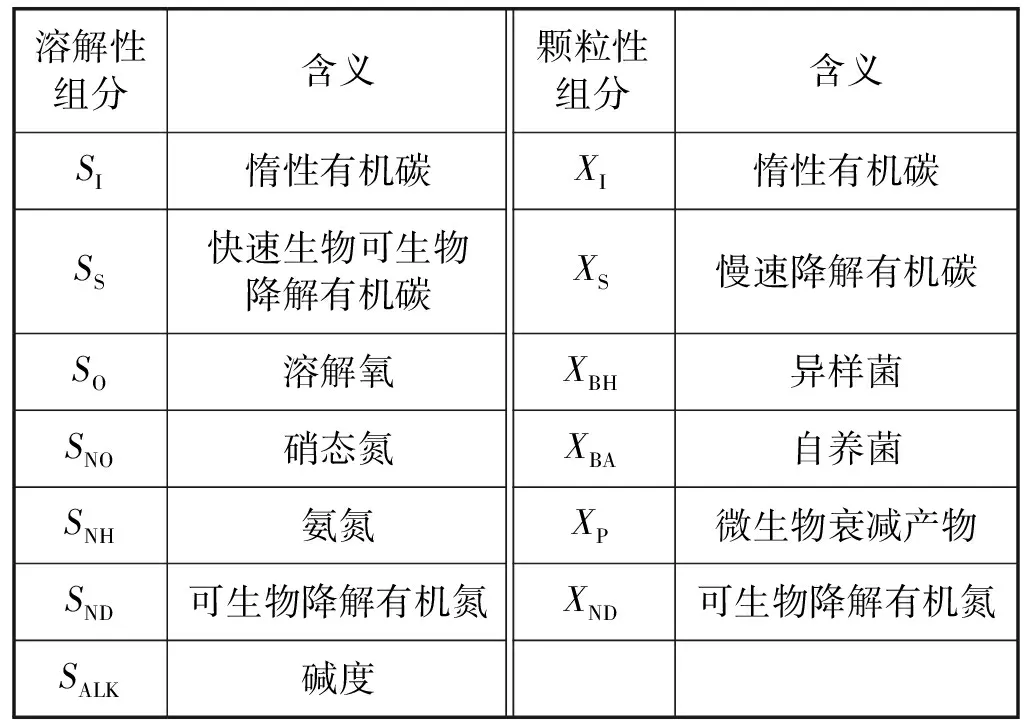
表1 反应器中状态变量

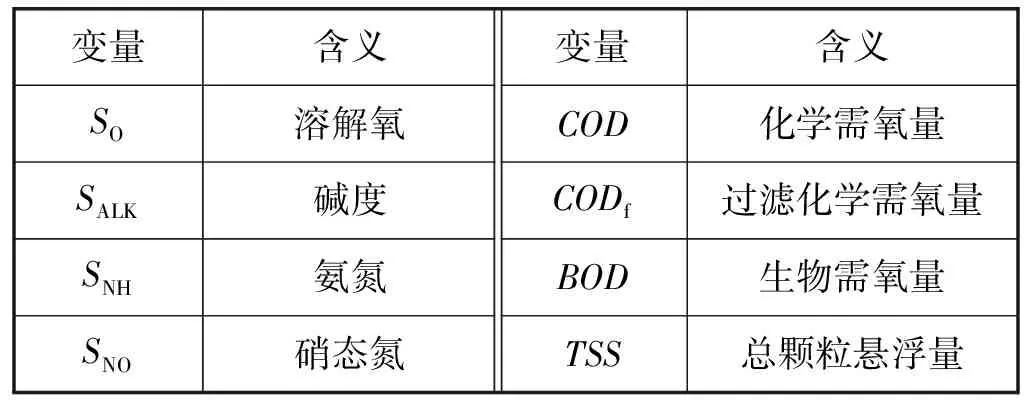
表2 测量输出量

首先比较了UKF、EFK方案在干燥天气下的性能，在本组仿真中78个状态变量分别产生零均值，标准差为0.2x0的高斯白噪声，并有界于[-0.2x0,0.2x0],测量传感器自带噪声为零均值，标准差为0.2y0的高斯白噪声，并有界于[-0.2y0,0.2y0]，y0=Cx0，其中：x0为初始状态值；y0为初始的测量值；C为输出测量矩阵。滤波方案所采用的初始估计值xinit均设置为1.02x0，根据协方差计算公式得出过程噪声和测量噪声的协方差矩阵分别为Q=diag((0.2x0)2)和R=diag((0.2y0)2)，初始的误差方差矩阵设为P(0)=Q，设过程噪声和测量噪声以及状态误差之间均不相关。图1为反应器3中实际过程状态和UKF和EKF的滤波轨迹。其中：虚线为EKF轨迹；点线为UKF轨迹；实线为实际过程状态轨迹。其他反应器和沉淀池具有与其类似的特点，可以看出EKF、UKF都能很好实现跟踪，大多状态跟踪效果都挺好，只有个别状态估计偏差较大如XI、XP、XBH。为了更加细致地比较EKF、UKF的性能优劣，我们需要定量计算一下二者在每个时间点的误差均值并绘成图像。比较方案将每组误差统一标准化之后采用RMS(Root Mean Square)。将整个时间段[t0,ts]两种方案每个状态的最大估计误差值作分母来标准化每个状态误差，t0、ts分别为初始时间和终止时间，状态误差如式(21)所示。

(21)

式中：ei(tk)为一个标准化的状态变量的误差序列，k为仿真时刻。计算78个状态在时间段[t0,ts]内每一个时刻的整体误差如式(22)所示。

(22)

采用误差均值及最大值来比较两种方案估计性能的优劣，计算公式如下：

(23)

Max|e|=Max(e(tk))

(24)

式中：K为[t0,ts]时间段计算的点数。根据式(21)-式(24)，通过定量计算EKF、UKF的误差均值分别为2.94、2.39，最大标准化误差分别为5.04、4.15，可以看出EKF给出的估计性能没有UKF好。干燥天气数据下UKF对比EKF性能大概提升了12.7%，图2为二者的误差轨迹，实线为EKF的误差轨迹，虚线为UKF误差轨迹，可以看到实线始终高于虚线，一开始二者比较相近，随着输入数据和仿真时长的增加，二者的曲线也在不断波动变化。

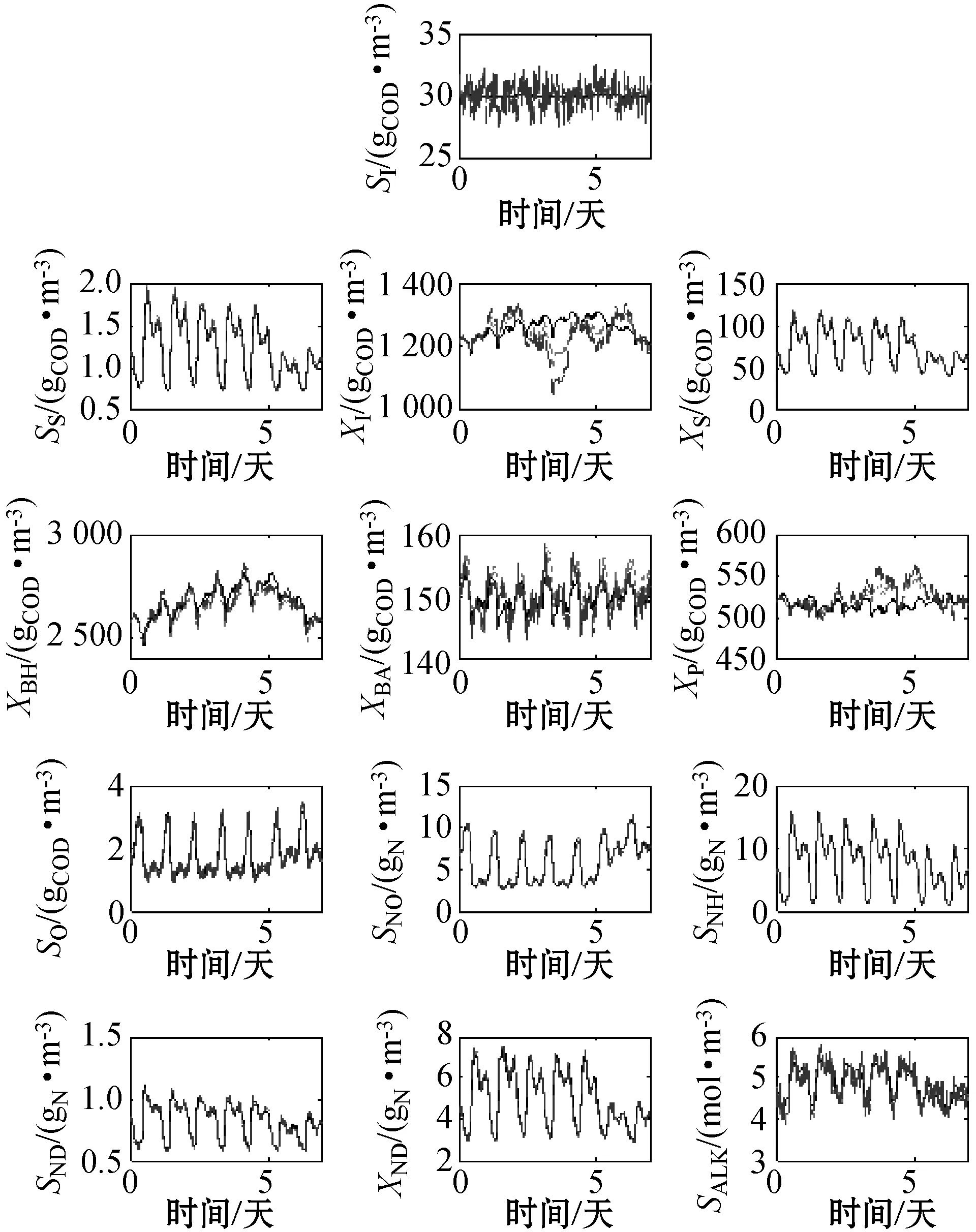
图1 干燥天气下反应器3中EKF轨迹、UKF轨迹、 实际过程状态轨迹

图2 EKF误差和UKF误差轨迹

在另一组的仿真中，在不同天气状况分别对两种估计方案的性能进行了测试。除了系统输入数据外，所有的条件都与上一组仿真完全相同。过程噪声取标准差为0.2x0的高斯白噪声，测量噪声取标准差为0.2y0的高斯白噪声，图3给出了雨天状况下反应器3中的13种成分的实际状态和两种估计方案的轨迹。其中：虚线为EKF轨迹；点线为UKF轨迹；实线为实际过程状态轨迹。其他反应器和沉淀池具有与反应器3类似的特点。此天气状况和当前噪声环境下，EKF、UKF的估计误差均值分别为2.6、2.26。UKF对比EKF估计精度提升了13.08%。暴风雨天状况下，EKF、UKF的估计误差均值分别为2.9、2.43，UKF较EKF估计精度提升16.2%。这表明了尽管恶劣天气下输入数据波动比较大，UKF算法仍然比EKF滤波算法的估计性能好。

图3 雨天状况下反应器3中EKF轨迹、UKF轨迹、 实际过程状态轨迹

在最后一组仿真中，通过改变过程噪声和测量噪声的大小来测试EKF、UKF性能的优劣，初始条件xinit仍设为1.02x0，通过参数wQ和wR来调整噪声的幅度，假设过程噪声大小为wQx0，并有界于[-wQx0,wQx0]，则Q=diag((wQx0)2)，测量噪声的大小为wRy0,并有界于[-wRy0,wRy0]，均为有界的高斯白噪声，有y0=Cx0，R=diag((wRy0)2)。初始误差方差阵P(0)=Q，不同大小过程噪声和测量噪声下EKF和UKF状态估计的误差均值如表3所示。可以看出在干燥天、雨天和暴雨天情况下，无论过程噪声及测量噪声大小如何改变，UKF估计性能始终优于EKF估计效果。

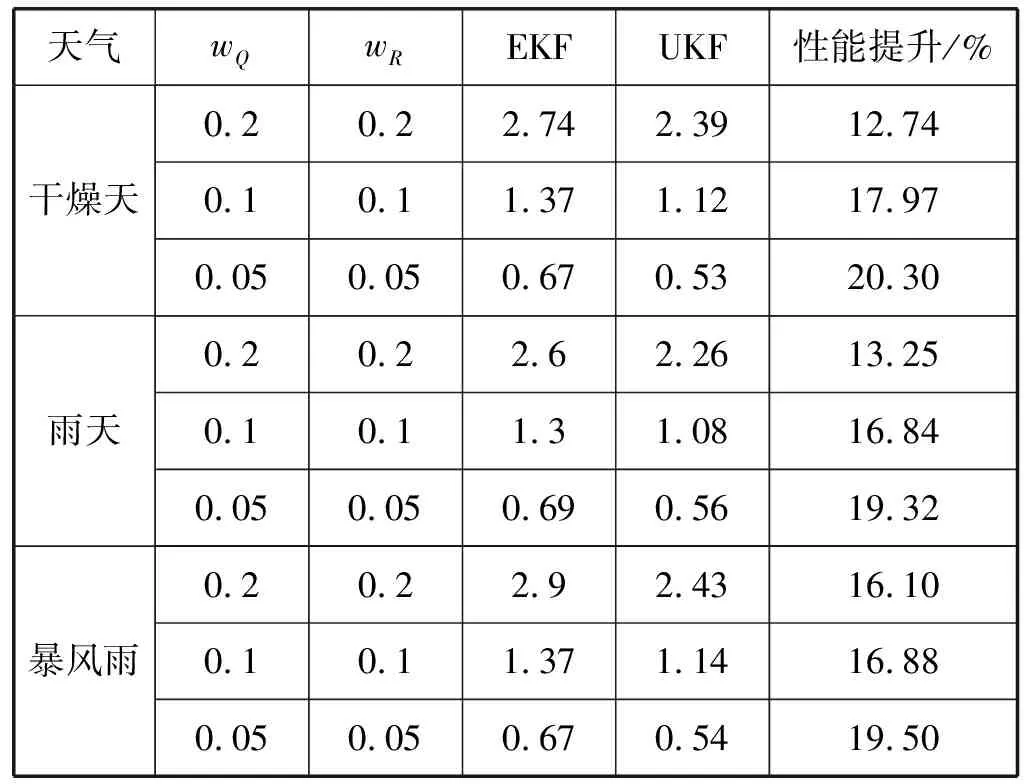
表3 不同噪声、天气条件下估计误差均值比较

4 结 语

无迹卡尔曼滤波算法通过对非线性函数的概率密度分布近似来完成估计过程，与扩展卡尔曼算法相比不需要对Jacobin矩阵进行求导，也没有忽略高阶项，因此对非线性系统的状态估计有较高的计算精度。本文将无迹卡尔曼滤波算法引入到污水处理过程带的状态估计问题中，并与扩展卡尔曼滤波算法相比较，结果表明无论天气状况如何，在相同模型噪声与测量噪声下的UKF估计精度始终高于EKF的估计精度，并且鲁棒性好，UKF较EKF的估计精度提升了10%～20%左右，显著提高了对复杂污水处理过程的状态估计效果。