基于SPH 算法的机翼油箱晃动分析

赵博伟，赖 辉

（成都飞机工业（集团）有限责任公司技术中心，四川 成都 610092）

液体的自由表面由于受到激励或外加扰动而产生的运动称为液体晃动。航空航天、船舶、石油化工及核动力等领域广泛存在液体晃动问题。在航空领域，飞机起飞、飞行及着陆过程中由于气动紊乱、发动机转子的不平衡、飞机发射等原因导致的油箱内燃油的晃动，会造成不良的影响。第一，晃动会使燃油循环往复地冲击油箱结构，产生冲击载荷，造成油箱结构的疲劳破坏[1]；第二，飞机全机的重心分布会受到燃油重心变化的影响，机翼上的重心分布也是影响飞机姿态稳定性的因素之一[2-3]。

因此，研究燃油晃动产生的冲击力、晃动力矩所引发的油箱结构强度问题，对于飞行器机翼油箱（尤其是某型无人机大展弦比机翼油箱）结构和强度设计可以提供一定的工程技术支持和指导。

本项目基于有限元分析软件ABAQUS，建立机翼油箱的有限元模型，并进行流固耦合动力分析，选用光滑粒子流体动力学（Smoothed Particle Hydrodgnamics，SPH）算法对机翼油箱进行燃油晃动下的仿真分析，判断其是否漏油，是否满足强度刚度要求。

1 计算方法

1.1 流固耦合

流固耦合力学是研究变形固体在流场作用下的各种行为以及固体位形对流场影响这两者相互作用的一门科学。按其耦合机理可分为两大类：一类为耦合作用只发生在两相交界面上，方程上的耦合是由两相耦合面上的平衡来引入的；二类为两域部分或全部重叠，建立方程需要针对具体物理现象，通过描述问题的微分方程来反映耦合效应。

1.2 SPH 方法

本文采用光滑粒子流体动力学方法，是一种无网格化的Lagrange（拉格朗日）算法，具有自适应、无网格、粒子形式以及拉格朗日单元的特征，避免了传统拉格朗日解法中的网格变形问题，适合处理大变形与冲击问题[4]。

拉格朗日形式的流体动力学N-S 方程可表示为：

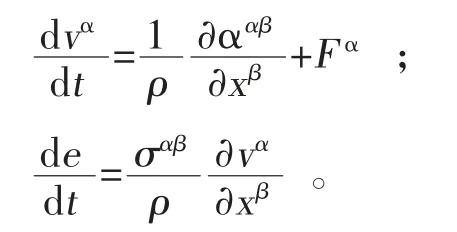
式中，F为单位质量的力；σ为总应力张量，由各项同性压力和黏性应力两部分组成。应用SPH 粒子近似法对动量方程进行变换可得如下表达式：

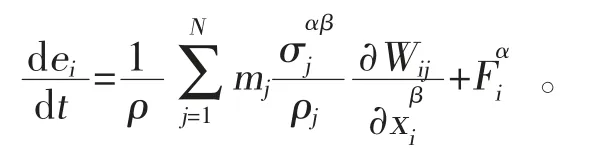
根据单位梯度SPH 核粒子近似式，对动量方程进行变换整理，并把总应力张量分解为各向同性压力和黏性应力，再用SPH 粒子近似法对能量方程进行变换整理，可得到能量方程的最终粒子近似式。

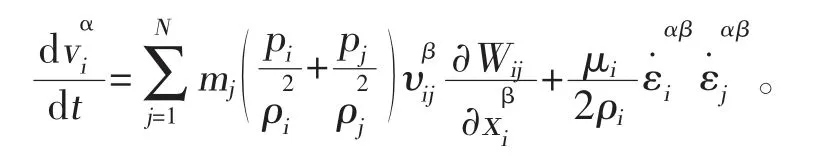
1.3 关键问题

为了准确模拟流体动力学问题，防止在冲击域内的求解结果产生非物理震荡，对SPH 算法进行特别处理，采用Monaghan 型人工黏度[5]。表达式如下所示。

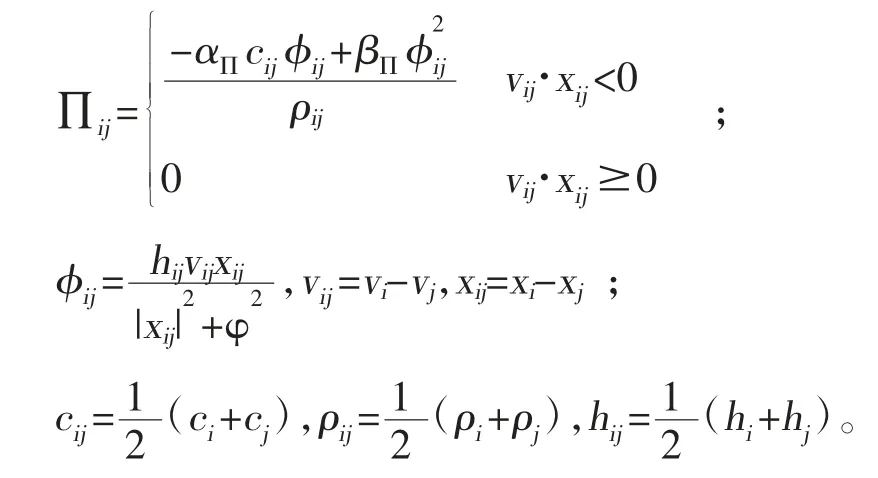
式中，αΠ和βΠ为常数，αΠ取值为1，βΠ取值为1 或者2，这2 个取值能有效地防止粒子的非物理穿透；c表示声速；v为粒子的速度矢量；为防止粒子相互靠近时发生数值发散，计算中引入因子φ=0.1hij。

使用SPH 方法进行流体模拟时，选取初始光滑长度会对计算结果有重要影响。对于油箱晃动中复杂流体大变形这种过程，必须考虑粒子间距的变化来重新计算适合的光滑长度。故使用按照平均密度来修正光滑长度的方法。

对不可压缩流，通过采用人工压缩率将其视为可压缩流，从而达到求解压力对时间导数的要求[4]。

2 晃动分析

2.1 计算模型

流固耦合计算中，将三维实体油箱模型简化为壳体模型，并且将多个部件合并为单一部件以提高计算效率。某型大展弦比无人机机翼油箱包括3 个独立的油舱，分别为左舱、中舱和右舱，基于模型及载荷的对称性考虑，取一半机翼进行分析（保留一半中舱及右舱），简化后，计算模型为上蒙皮，框架及下蒙皮共3 个。机翼油箱采用铝板及复合材料板，具体参数如表1 所示。机翼油箱的复合材料采用横向各向异性板建模，其纤维纵向（0°方向）沿着机翼后梁轴线方向。材料分配和板厚如表2 所示。

表1 材料参数

表2 机翼油箱部件材料分配和板厚

燃油为航空燃油，考虑2 种充油量：多油（68%）和半油（50%），如表3 所示。

表3 机翼油箱充油量具体参数

为减少机翼油箱模型的单元数及单元尺寸，对油箱采用四节点的缩减积分壳单元（S4R）和三节点壳单元（S3）进行划分，燃油采用PC3D 粒子单元（由C3D8R实体单元转换）。其中机翼油箱单元数为22 655，燃油单元数根据多油及半油分别为63 466 和45 694。机翼油箱燃油及单元划分如图1 所示。

图1 机翼油箱燃油及单元划分

机翼油箱晃动周期为0.32 s，最大转角0.262，初角速度3.50 m/s，最大角加速度为408.5 m/s2，变速历时0.018 s。不考虑冲压作用，机翼油箱的对称面，运动耦合在参考点上，对参考点施加绕着x轴的角加速度和初角速度。在靠近转角峰值时，转动减速，随后反向加速。油箱及燃油都施加重力载荷且相互之间切向无摩擦接触，法向硬接触。

2.2 仿真计算

机翼油箱晃动采用SPH 算法，使用ABAQUS/Explicit求解器进行求解。前文提到过机翼油箱的材料为复合材料及铝材。

2.2.1 半油晃动应力和应变

在半油晃动过程中，铝材的最大Mises 应力为66 MPa，纤维材料的最大纵向应力为45 MPa，最大横向应力为17 MPa，均满足强度要求。最大横向应变为2 054 με。最值点时，部分部件的应力和应变分布如图2-图4所示。各部件最大应力应变如表4 所示。

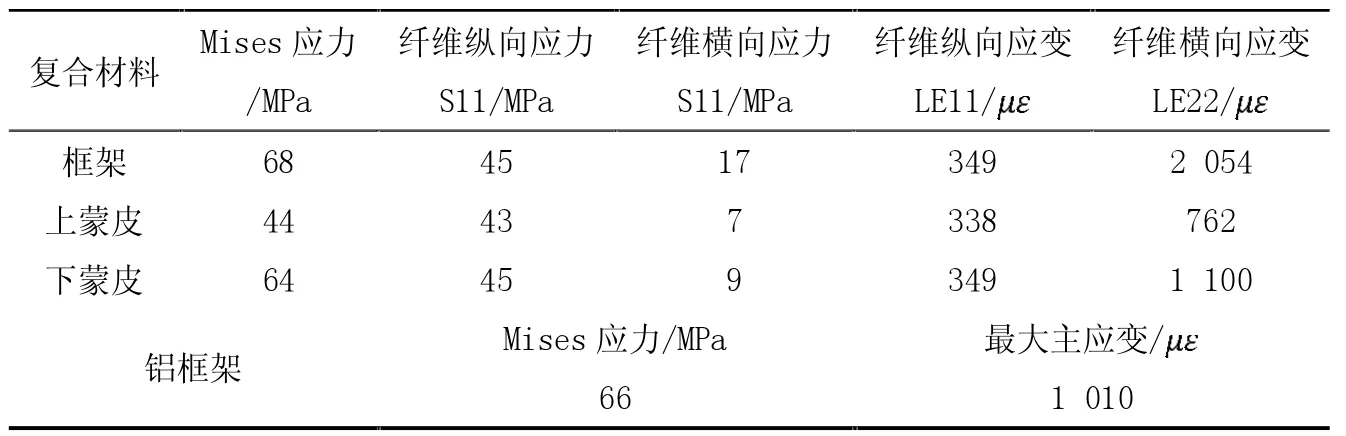
表4 各部件最大应力应变

图2 半油晃动，机翼下蒙皮的应力应变在最值点时的分布

图3 半油晃动，机翼框架铝材的应力应变在最值点时的分布

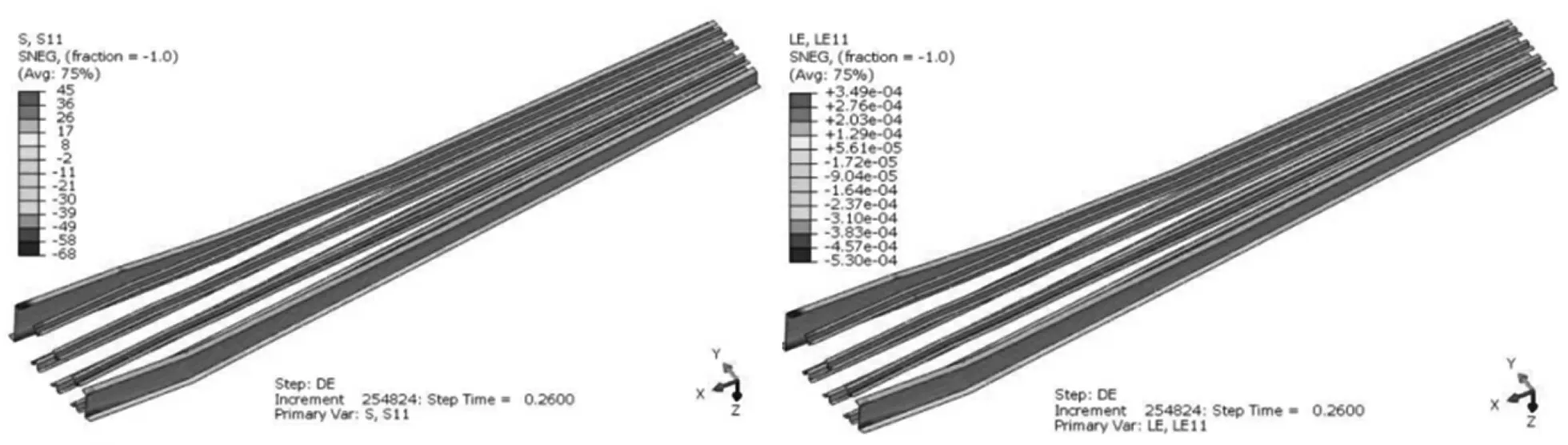
图4 半油晃动，机翼框架复合材料的应力和应变在最值点时的分布

2.2.2 半油晃动速度与位移

机翼油舱的最大粒子速度为6.100 m/s（中油舱）以及3.400 m/s（右油舱），以及机翼油箱质心的最大偏移为0.020 mm（x方向），0.550 mm（y方向），1.650 mm（z方向）。质心偏移很小。而油箱整体保持稳定，机翼油箱在晃动过程中刚体运动占主导，局部变形（挠度）很小。机翼油箱的连接单元处，两表面间相对位移均小于0.250 mm，可以预计不会发生燃油泄漏。

2.2.3 半油晃动压力

机翼两油舱各壁面最大的瞬时平均压力位于中油舱1 段的下壁面，为0.032 MPa，但仍小于机翼油箱的冲压荷载0.043 MPa。各区段的平均压力变化在位移峰值过后（0.100 s 和0.260 s 附近）出现压力的峰值。前壁面和下壁面的平均压力较大（表5）。

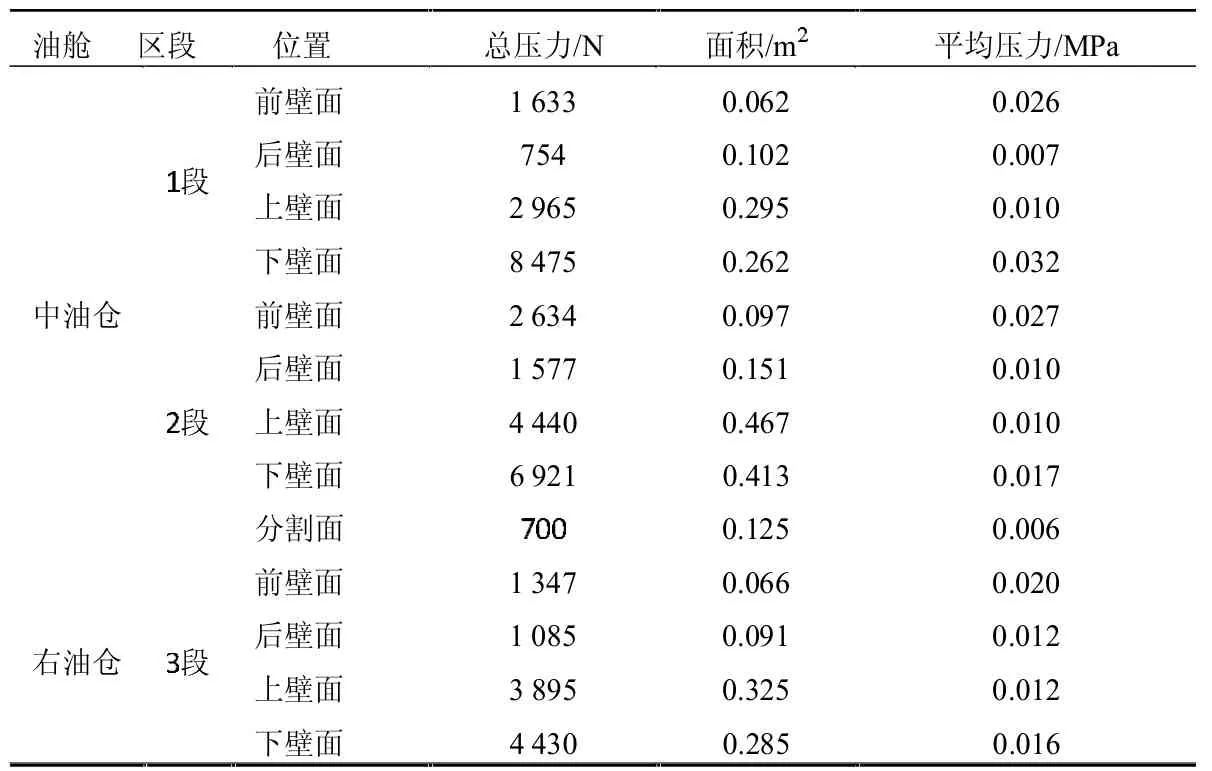
表5 机翼两油舱各壁面的最大总压力和平均压力

2.2.4 多油晃动应力和应变

在多油晃动过程中，铝材的最大Mises 应力为89 MPa，纤维材料的最大纵向应力为85 MPa，最大横向应力为18 MPa，均满足强度要求。最大横向应变为2 075 με。最值点时，各部件的应力和应变分布如图5-图7 所示。各部件最大应力应变如表6 所示。

表6 各部件最大应力应变

图5 多油晃动，机翼下蒙皮的应力应变在最值点时的分布

图6 多油晃动，机翼框架铝材的应力应变在最值点时的分布

图7 多油晃动，机翼框架复合材料的应力和应变在最值点时的分布

2.2.5 多油晃动速度与位移

机翼油舱的最大粒子速度为6.600 m/s（中油舱）以及3.60 m/s（右油舱），以及机翼油箱质心的最大偏移为0.020 mm（x方向），0.330 mm（y方向），1.420 mm（z方向）。质心偏移很小。而油箱整体保持稳定，机翼油箱在晃动过程中刚体运动占主导，局部变形（挠度）很小。机翼油箱的连接单元处，两表面间相对位移均小于0.250 mm，可以预计不会发生燃油泄漏。

2.2.6 多油压力

机翼两油舱各壁面最大的瞬时平均压力位于中油舱1 段的前壁面，为0.028 MPa，但仍小于机翼油箱的冲压荷载0.043 MPa。各区段的平均压力变化在位移峰值过后（0.100 s 和0.260 s 附近）出现压力的峰值。前壁面和下壁面的平均压力较大（表7）。

表7 机翼两油舱各壁面的最大总压力和平均压力

2.3 小结

本文中对机翼油箱晃动考虑了多油（68%）和半油（50%）2 种充油量。油箱的应力和应变峰值均小于材料的拉伸强度，满足强度要求。其中多油较半油的应力和应变较大。连接单元处的最大相对位移均小于0.250 mm，不会发生漏油。晃动过程中，刚体运动占主导，蒙皮和框架的变形很小，两油舱各壁面的最大平均压力均小于机翼油箱的冲压载荷，多油较半油的平均压力峰值较小。

3 结论

本文以某型大展弦比无人机机翼油箱晃动分析为背景，选用高效的SPH 算法应用通用有限元分析软件ABAQUS 对机翼油箱的充液晃动进行仿真分析，通过数据研究表明，机翼在油箱晃动过程中满足强度要求，变形微小，整体稳定。文中的数据论证对于飞机总体设计、航天器推进贮箱的防晃设计等工作具有一定的理论价值和工程指导意义。