校验用开合式霍尔电流传感器聚磁环设计

张涵竹，李岩松，刘君

(华北电力大学(北京) 电气与电子工程学院，北京 102206)

0 引 言

在智能电网的建设中，要求定期对电流互感器进行校验，从而保证设备对电流数据的精确测量[1]。霍尔电流传感器的优点是体积小、无触点、测量结果精确[2]，将其制作成高精度、高灵敏度的标准电流传感器，能很好地满足校验要求。在线校验可在不断电的情况下进行，提高了供电系统的可靠性，而传统霍尔电流传感器的磁环只开单段气隙，灵敏度较低，无法穿过线路进行在线校验操作。无铁芯霍尔电流传感器能避免铁芯磁滞效应和饱和的影响[3]，然而很难保证霍尔元件平面与被测导线平面保持绝对水平，容易因平面角度差而出现测量误差。常见的开启式霍尔电流传感器磁环选择坡莫合金材料[4]，聚磁效果仍有提升空间，且没有探讨气隙长度与磁环长度的具体比例关系，其精度也只能达到0.5级。在磁环表面附着一层钴基合金薄膜可以有效提升磁场检测的灵敏度[5]，然而钴合金价格昂贵，此种磁环暂时只适用于实验室场合。利用开气隙铁芯和无缝铁芯分别测量直流、交流量的双铁芯霍尔电流传感器能提高测量精度并保持了较好的线性度[6]，但未涉及铁芯横截面大小的讨论。鉴于此，本文提出一种基于铁基纳米晶合金的开合式圆形聚磁环结构，利用此种结构的标准霍尔电流传感器能方便地进行现场校验。与单气隙聚磁环结构相比，其灵敏度更高，测量线性广度更宽；在常见的开启式传感器基础之上，加入了对气隙长度和磁环长度比例关系的讨论，并研究了磁环横截面积对测量精度的影响。

1 闭环霍尔电流传感器机理

闭环霍尔电流传感器引入了零磁通原理组成负反馈系统[7]。如图1所示，提高放大倍数，将放大电路的输出经功率放大，再输出补偿电流流过补偿线圈，其产生的磁场和被测电流产生的磁场方向相反，当两个磁场相等时，整个闭环达到动态平衡，数学表述为：

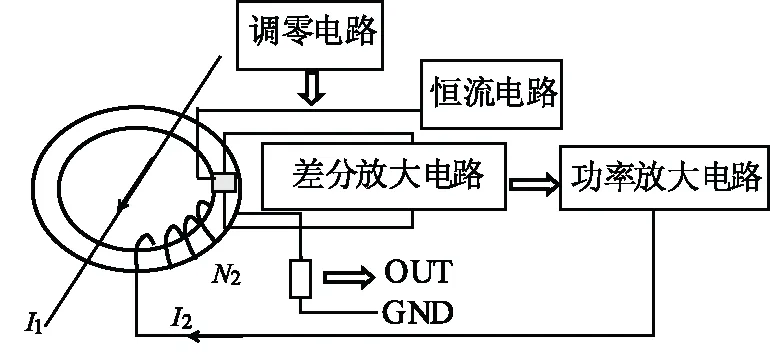
图1 闭环霍尔电流传感器机理图Fig.1 Mccjamism diagram of closed-loop Hall current sensor

N1I1=N2I2

(1)

式中N1为承载被测电流的导体匝数，无限长单根输电线路中N1为1；I1为被测电流；N2为反馈绕组的匝数，I2为反馈绕组中的补偿电流。

2 开合式聚磁环设计

由1节可以看出，传统的闭环霍尔电流传感器聚磁环采用单段气隙结构，而本文提出的开合式聚磁环结构如图2所示，与只开单段气隙的聚磁环结构不同之处在于，在磁环对称两侧均开有一段气隙，其中一段气隙σ1内放入霍尔元件，另一段气隙σ2用于开合操作。此种结构适用于互感器在线校验操作，能方便地穿过被测导线而不用夹断线路等复杂工序。从聚磁环材料、横截面积以及气隙长度出发，改进设计方法，提高其测量精度和灵敏度。

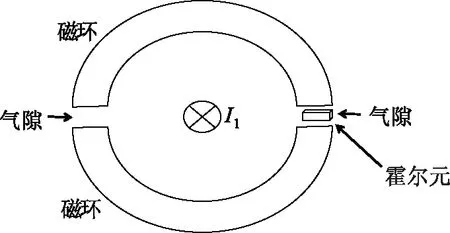
图2 开合式聚磁环结构图Fig.2 Structure diagram of open-close magnetic ring

2.1 材料特性分析

霍尔电流传感器的聚磁环是整个传感器的重要组成部分，其材料性能直接关系到测量结果的精确性[8]。由于本文介绍的霍尔电流传感器需要进行互感器校验操作，聚磁环必须采用聚磁效果强的材料，才能保证足够的灵敏度。如表1所示,常见的铁磁材料：铁镍钼合金、铁硅铝合金、铁镍合金、铁氧体及硅钢片等，其中铁镍钼合金和铁镍合金成本较高，经济适用性不强；铁硅铝合金的铁损较大，温度稳定性不高；利用硅钢片制成的铁芯往往需要堆叠成片，要求其制造工艺很高，同时还存在漏磁现象。

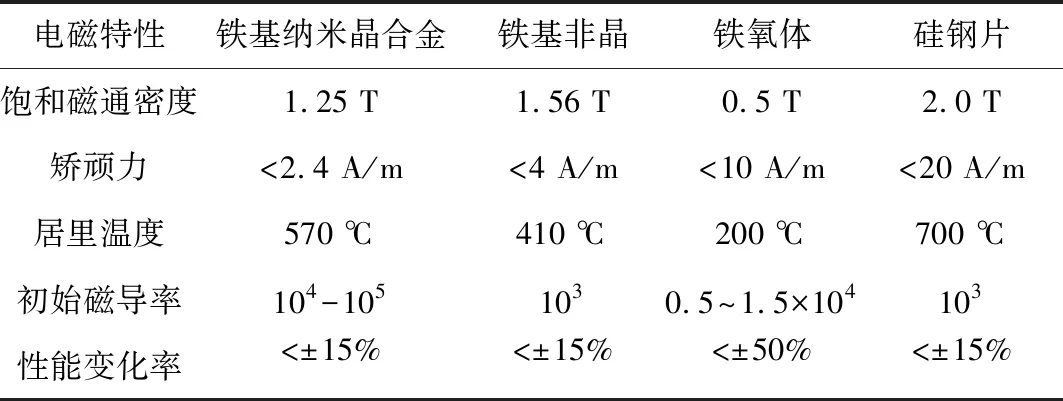
表1 几种磁性材料对比Tab.1 Comparison of several magnetic materials

本文中的聚磁环采用铁基纳米晶合金材料，它具有磁导率高、损耗小、矫顽力小等多种优势[9]。纳米晶是基于非晶态结构，并采用特别的热处理让其塑成晶核然后扩张，同时保持晶粒体积在nm数量级，不能变成完全态的晶体，此时的结构就被称为纳米晶。目前来说，铁基纳米晶合金是互感器应用中性能最优异的软磁材料[10]。

铁基纳米晶合金与其余两种材料的磁化曲线(T=25 ℃、f=10 kHz时)对比如图3所示。

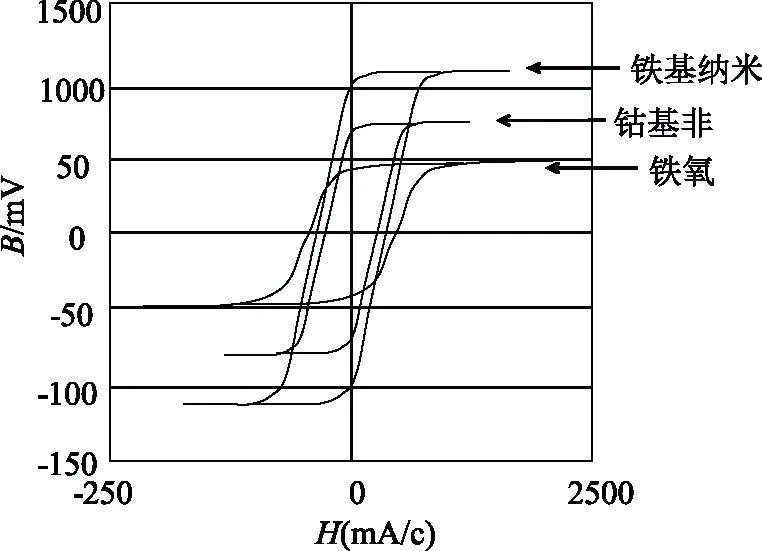
图3 磁化曲线对比图Fig.3 Comparison chart of magnetization curves

可以看出，铁基纳米晶合金各项特性都十分优异，尤其是高磁导率、低损耗的特性，能提升互感器校验的灵敏度与精度。而且磁性能极好，完全可以和非晶合金中性能最好的钴基非晶合金相提并论[11]，但却不含昂贵的钴，所以价格相对低廉。

2.2 磁环横截面

本设计中，聚磁环采用圆形截面。霍尔传感器放置于气隙中心处，其几何中心点与横截面圆心处于同一垂直线上。霍尔传感器放置位置的磁场分布均匀性会影响测量结果精确度，若磁环横截面积变化，气隙处的磁场分布也会出现变化。对不同横截面积下气隙处磁场分布情况进行分析，探讨了合理的横截面设计方法，尽量保证磁场在霍尔元件放置位置的均匀性。

在上述指定区域放置霍尔元件，并在此区域周围留出一定的裕度，定义均匀系数γ表示磁场的分布情况[12]，表达式为：

(2)

式中γ表示此区域内的最大磁感应强度Bmax与最小磁感应强度Bmin之差与Bmax的比值，γ的值越接近0，表示此区域的磁场分布越均匀。在COMSOL中建立截面积仿真模型，模型中两段气隙总长度保持在4 mm，磁环横截面的半径r由5 mm增大到10 mm，根据仿真结果计算出不同磁环横截面半径下的磁场均匀系数，得到磁场均匀系数γ与磁环横截面半径r的关系如图4所示。

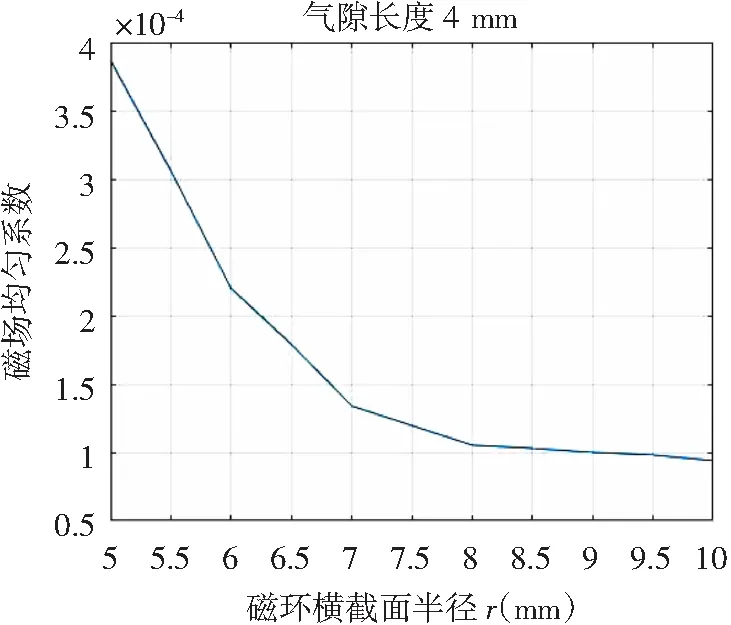
图4 磁场均匀系数与磁环半径r的关系曲线Fig.4 Relation curve between uniformity coefficient of magnetic field and radius r

从图4中可以得出，磁场均匀系数随着磁环横截面半径的增大而减小，表明横截面积越大，磁场分布更均匀；横截面积越小，磁场分布更杂乱。若为了使测量结果更精确，一味地增大磁环横截面积是不可取的，还需要考虑多种其他因素，比如磁环材料的消耗量以及整个传感器的重量和体积。磁环的横截面积越大，材料的消耗量就越多，传感器的重量和体积也就随之增大，会造成成本上升和校验操作的不便；同时缠绕在磁环上的反馈线圈长度也会随磁环截面的增大而增大，反馈线圈的尺寸、成本也会随之变大。但从机械强度方面来考虑，磁环的横截面越小，其机械强度越弱，不利于整个传感器架构的支撑。

所以，磁环横截面积大小应综合考虑以上因素，在不降低传感器机械强度的同时又尽量实现霍尔元件区域内磁场的均匀分布，从而提升测量精度。算出r=8 mm时磁场均匀系数约为1.0525×10-4，此时基本能保证霍尔元件位于均匀磁场之中。

2.3 气隙长度

2.3.1 气隙效应分析

本文中传感器聚磁环开有两段气隙，且两段气隙长度σ1、σ2相等，即σ1=σ2=σ，两段磁环实际有效总长度为lf，假设穿过磁环中心的导体匝数为N，流经每条导体的电流大小为I，由全电流定律可知：

NI=Hflf+Hg×2σ

(3)

式中Hf为两段磁芯中的磁场强度(假设磁芯内部Hf处处相等);Hg为两段气隙中的磁场强度(假设两段气隙中Hg处处相等)。气隙长度相对于磁环的截面积很小，气隙边缘漏磁通的影响可以忽略不计，并且认为磁环中的磁感应强度Bf与气隙中的磁感应强度Bg相等，则式(3)可写为：

(4)

式中μ0为空气的磁导率;μr为磁环材料的磁导率，定义μe为磁环总体的有效磁导率。由(4)式可以清楚地看出，增加两段气隙之后磁路的等效磁导率减小；且随着气隙宽度的增加，等效磁导率会越来越小，磁环整体的聚磁效果降低。

但由于两段气隙的存在，气隙磁阻远大于磁环磁阻，所以削弱了磁环材料的非线性，扩大了霍尔电流传感器的线性测量范围。当气隙长度设置合理时，由于气隙的去磁作用，磁环剩磁感应(Br)减小，传感器的线性回差也会有所降低。

2.3.2 磁势变化

磁环与气隙中主要存在以下三类磁通：流通在磁环内的主磁通、由气隙磁势产生的漏磁通、由相邻磁环之间的磁势差产生的旁路磁通。如图5所示，当漏磁通穿过反馈绕组时，会产生大小由磁势决定的涡流损耗。气隙段数与长度的不同会引起气隙磁势的变化，进而影响到反馈绕组中的损耗大小，而此损耗对测量精度会产生影响。

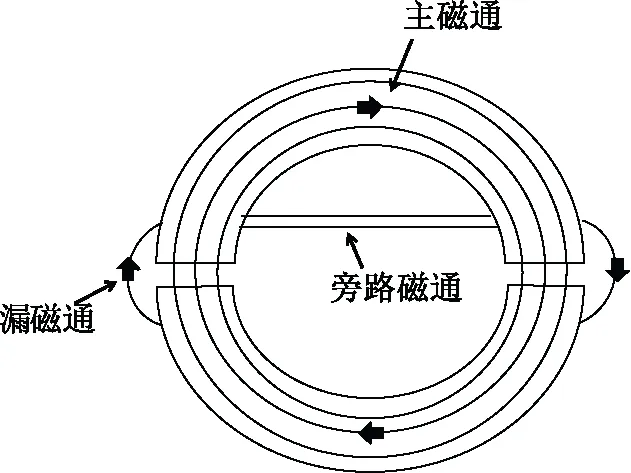
图5 磁通类别Fig.5 Types of flux

单气隙与开合式的磁环磁势降落对比如图6(a)和图6(b)所示。其中单气隙磁环的气隙长度为开合式磁环每段气隙长度的两倍。

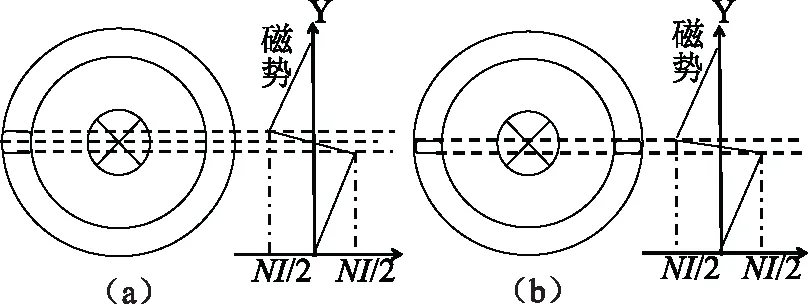
图6 两种磁环磁势降落示意图Fig.6 Schematic diagram of magnetomotive force drop of two rings

不管是单气隙还是开合式的磁环结构，气隙上的磁势降落均为总安匝数的一半。不同之处在于，因开合式结构中每段气隙长度为单气隙结构的一半，在两者的旁路磁通几乎一样的情况下，开合式的漏磁通要小于单气隙的漏磁通，使得反馈绕组中的损耗较单气隙结构更小，同时测量精度受损耗的影响也变小，这也是开合式聚磁环结构的优势之一。

2.3.3 长度比例

两段气隙中的磁感应强度Bg与反馈绕组中的电流I2之间存在一个较小相移角β，其大小可表示为：

(5)

式中p为磁环损耗；s为磁化功率；μr为磁环材料的相对磁导率；λ为两段气隙总长度与两段磁环磁路长度的比值，即λ=2σ/lf，ψ表示损耗角。μr和λ的增大都会引起 tanβ的减小，从而提高传感器的测量精度，所以需要采用高相对磁导率的磁环材料以及设计合理的气隙长度。

由全电流定律，并引入系数ω，表示反馈绕组电流产生的磁感应强度B2与磁环系统之间的非线性误差，可得出：

ω=μr/(μr+1/λ)

(6)

B2=NIμ0ω/lf

(7)

将霍尔电流传感器的输出UH作为基准值，计算输出电压的误差结果如下：

(8)

式中Bn和In分别表示基准值下对应磁感应强度和反馈电流的大小;φ为UH和I2间的相位角。将cos(φ-β) 展开，且认为β≈sinβ≈tanβ，则式(8)可化为：

(9)

由于误差系数ω为常数，再利用和差化积公式可将式(9)化简为：

(10)

分析可知式(10)在φ=(π-β)/2 和φ=(3π-β)/2时取得最大值ΔUmax：

(11)

磁环的相对磁导率μr和损耗角ψ在选定磁环材料后就已确定下来。若已知允许的最大电压误差值为ΔUmax，可计算出相移角β的大小，再结合式(5)，可推导出每段气隙长度与磁环有效长度的比值：

(12)

式(12)表明，在选定磁环的大小后，即可大致算出每段气隙的合理长度，或者先确定气隙长度，再推算出磁环的长度，而具体的数值可进行仿真微调，经过成本及测量精度对比之后再确定。

3 实验结果及分析

运用有限元(FEM)方法[13]，在COMSOL Multiphysics软件里对开合式聚磁环结构霍尔电流传感器进行3D建模。模型中，聚磁环材料选用铁基纳米晶合金Fe85.5Zr2Nb4B8.5，其相对磁导率为60 000，电导率为1.25×10-6。聚磁环横截面半径为8 mm，环平均半径为10 cm，结合式(12)并考虑霍尔元件本身的厚度，将两段等宽气隙长度设为2 mm。

通过改变被测电流I1的数值，使总安匝数NI发生变化，再测出霍尔传感器所在气隙内磁感应强度Bg的大小。为方便比较，同时测出相同条件下单气隙和中心对称的四气隙聚磁环结构的气隙磁场强度，观察三种磁环的不同。三种磁环内气隙总宽度均为4 mm。三种气隙结构仿真局部图如图7所示。

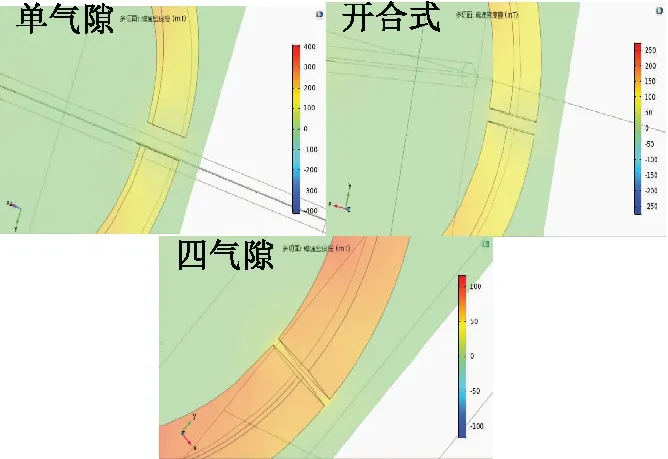
图7 三种气隙结构仿真局部图Fig.7 Partial simulation graphs of three structures

根据测得的磁感应强度值，最终绘制出总安匝数NI与气隙磁感应强度Bg的关系曲线如图8所示。

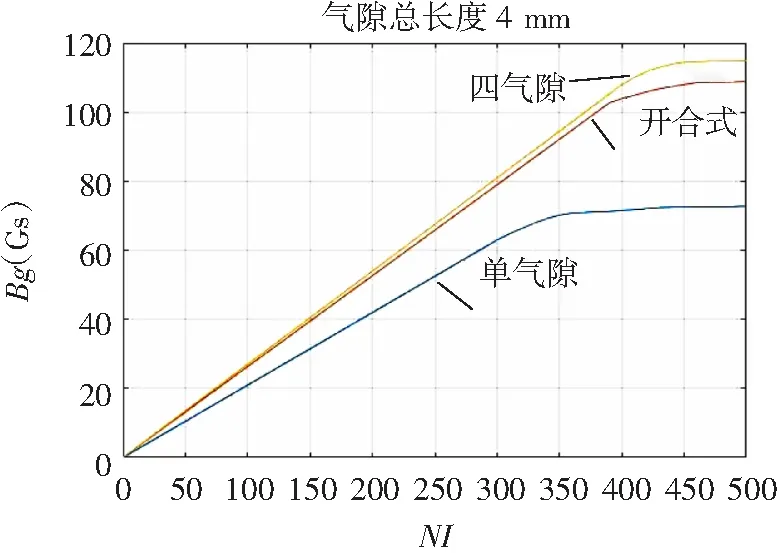
图8 气隙磁场强度-总安匝数曲线Fig.8 Bg-NI curves

从对比图可看出，由于漏磁通的减小，相同NI下，开合式磁环的气隙磁感应强度要明显大于单气隙磁环的气隙磁感应强度，但略低于四气隙磁环的气隙磁感应强度，说明开合式聚磁环结构霍尔电流传感器的灵敏度得以提高。不仅如此，与单气隙聚磁环结构相比，开合式聚磁环结构还拓宽了传感器的线性测量范围。

同时注意到，无论是从线性测量范围还是灵敏程度来评判，四气隙聚磁环结构的性能表现均比开合式聚磁环结构更优异，但两者的差别几乎可以忽略。若采四气隙聚磁环结构，对四段磁环的加工难度比开合式结构更高，在磁环上绕制反馈线圈更困难，同时给磁环的固定带来不便，这样就增加了在线校验操作的复杂性。综上所述，从灵敏度、测量的线性范围广度和加工安装方便性来讲，开合式聚磁环结构都有一定的优势。

4 结束语

文中提出的开合式聚磁环结构选择铁基纳米晶合金作为聚磁环材料，与常见的开启式霍尔传感器磁环材料相比，铁基纳米晶合金磁导率更高、损耗却有所降低；同时结合磁场均匀系数，设计合理的横截面积，保证传感器具有较高的测量精度。该结构中一段气隙用于开合操作，进行互感器现场校验时能方便地穿过线路，克服了单气隙聚磁环结构的弊端。三种磁环对比实验的结果表明，开合式相比于单气隙聚磁环结构，其线性测量范围更广，且灵敏度更高。实验结论为今后进行现场在线校验提供参考。