基于正交设计的围岩力学参数对围岩稳定性影响分析

胡森林 王桂生

（1.河海大学农业科学与工程学院 南京 210098 2.中水淮河规划设计研究有限公司 合肥 230601）

1 敏感性分析原理

敏感性分析是指测定敏感因素在可能的取值范围内变动时所导致的评价指标的变化程度。根据敏感因素的数量，又分为单因素敏感性分析和多因素敏感性分析。单因素敏感性分析是假定其他因素不变，计算分析一个因素变化对考核指标的影响程度。多因素敏感性分析是假定其他因素不变，计算分析有两种或两种以上敏感因素变化对考核指标的影响程度。敏感性分析的步骤如下：

（1）选择研究对象，分析该系统的特性，确定影响该系统特性的因素，并对因素的取值拟定数据，称之为因素水平。

（2）拟定因素变化导致的系统特性变化考核的指标量，即确定系统考核指标。

（3）确定敏感性分析方法。可以通过单因素敏感性方法研究，其具有试验数量少的优点，但是没有考虑各因素之间的相互作用对系统特性的影响。除了单因素敏感性分析，还可以采用多因素敏感性分析法，其优点是考虑了各因素的协同作用，对系统特性的影响，但是具有试验方案多、工作量大的缺点。

（4）数据分析。对试验方案得到的数据进行处理，多因素敏感性分析通常采用极差分析方法确定不同因素对考核指标的影响程度。

2 隧洞开挖模拟有限元理论

隧道开挖破坏了地层中的初始应力状态，使得在隧道开挖面上出现了应力释放。用以模拟不同施工阶段的力学性态的有限元方程可写为：

（[K0]+[ΔKi]）{Δδi}={ΔFir}+{ΔFia}

式中：[K0]—地层开挖前岩土体等的初始总刚度矩阵；[ΔKi]—施工过程中岩土体和支护结构刚度的增量或减量，其值为挖去岩土体单元及设置或拆除支护结构单元的刚度；{Δδi}—任一施工阶段产生的节点增量位移列阵；{ΔFir}—由开挖释放产生的边界增量节点力列阵，初次开挖由岩土体自重、地壳变形构造应力、地下水荷载、地面超载等确定，其后各开挖步骤由当前应力状态决定；{ΔFia}—施工过程中增加的节点荷载列阵。

3 工程应用

3.1 工程背景

驻马店市东区城市供水工程—薄山水库取水口工程主要由库区引水隧洞、库岸竖井、山体输水隧洞及坝后输水洞出口控制室四部分组成，输水隧洞位于原泄洪洞西侧约76m 处，基本与泄洪洞平行，洞水平长度320m，洞径2m，洞进口底高程91.00m，出口底高程87.90m，进出口高差3.10m。依据开掘隧洞时的施工地质编录资料，自进口至出口岩性分布见表1。

表1 输水洞沿线地质情况表

根据工程勘探资料，薄山水库取水口工程输水隧洞敏感性分析基本参数如下：弹性模量E=3.5GPa，变化范围为2.5～3.5GPa， 泊松比μ=0.33，变化范围为0.25～0.35，粘聚力c=29kPa，变化范围为25～35kPa，内摩擦角=32°，变化范围为20°～30°。

3.2 设计方案

围岩稳定性主要与围岩的弹性模量、泊松比、摩擦角、粘聚力、埋深等几个因素有关。在工程实际中，有很多因素影响上述参数的大小，从而其取值的准确性直接决定了工程设计的可靠性。本文选择0+000-0+010 段全风化流纹质凝灰岩为研究对象，通过隧道开挖施工阶段分析，分析围岩弹性模量、泊松比、粘聚力、摩擦角对围岩稳定性的影响程度。

本文采用多因素敏感性分析的方法研究上述围岩力学参数对围岩稳定性的影响。由于多因素敏感性分析，需要大量的试验，工作量大，故利用正交试验设计原理来进行方案设计，减少工作量。正交试验设计是利用数理统计原理处理多因素试验的科学方法，在岩土和边坡工程得到了广泛的应用。其优点是能够通过代表性很强的少数次实验，确定因素对试验指标的影响程度。

根据工程勘探资料提供的围岩物理力学参数的变化范围，对围岩弹性模量、泊松比、粘聚力、摩擦角分别取3 个水平，见表2。

表2 影响因素取值表

选择拱顶下沉位移，拱腰收敛位移、塑性区半径为考核指标，根据L9（34）正交表确定计算方案见表3。

表3 计算方案表

3.3 有限元分析

薄山水库输水隧洞是圆形断面，半径为1m，采用全断面法开挖。在有限元建模时，取开挖进尺1m，四周边界为5 倍的洞直径。采用摩尔库伦准则，共划分单元4554 个，节点4950 个。

根据表3 提供的计算方案，通过Midas GTX NX分别模拟计算，得到方案1-9 隧道开挖典型断面拱顶下沉位移值、拱腰收敛位移值、塑性区半径见表4。

3.4 结果分析

敏感性分析研究一般通过极差分析和方差分析的方法对数据进行处理。其中，极差分析是普遍采用的方法，其大小反应因素对考核指标的影响程度。设定水平数a（a=1，2，3），因素b（b=1，2，3，4），Kab表示为第a 个水平下，第b 个因素试验所得结果的平均值。则极差Rb的大小等于同一影响因素下各水平的Kab的最大值与最小值之差。根据表4 记录的拱顶下沉位移、拱腰收敛位移、塑性区半径数据，经过计算得到弹性模量、泊松比、粘聚力、摩擦角4 个因素所对应的极差值及变化趋势如图1 所示。

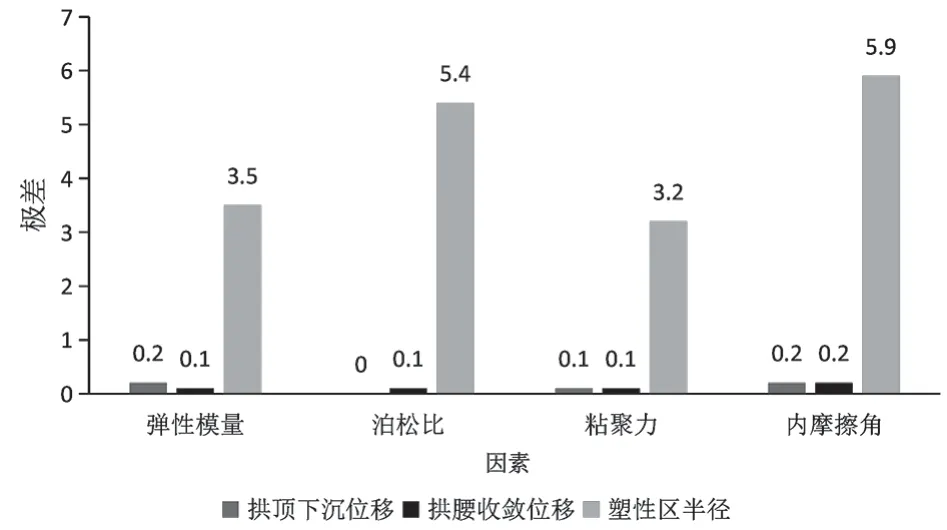
图1 极差分析结果图

表4 有限元计算结果表

4 结论

通过对数据进行极差分析，可以得出以下结论：（1）对拱顶下沉位移而言，弹性模量和内摩擦角是主要影响因素，其参数变化对计算结果影响较大。（2）拱腰收敛位移对弹性模量、泊松比、粘聚力3个因素不敏感，可见在当前参数变化范围类，改变上述参数值对数值计算结果影响不大。（3）对于塑性区半径，围岩物理参数的敏感性由大到小依次为：内摩擦角、泊松比μ、弹性模量E、粘聚力c。其中，内摩擦角和泊松比的取值对计算结果的影响最大。因此，在工程勘察时，最好结合现场试验确定围岩物理力学参数，从而确保其取值的可靠性，保证工程设计的安全性■