应急救援中心的选址-调度的双层模型及混合嵌套式算法
孙 硕,孟 晗,马 良,刘 勇
(上海理工大学 管理学院,上海200093)
1 引 言
近年来大规模自然灾害频发,为及时抢救灾区人民的生命,降低灾害造成的损失,建立与研究应急物流体系已是刻不容缓.其中,应急物资调配是应急物流环节中最关键的一个环节,关系到应急物资能否准确、高效地被运输到受灾点,同时也关系到救援工作的成败与否.
针对灾后应急物资调配问题,国内外学者进行了大量研究:Sheu[1]以需求满足率最大和成本最小为目标建立了应急物资储备库模型,并设计了动态规划算法求解;郭静文等人[2]以消防站数量能覆盖所有火灾需求点和尽可能最小化建设成本为目标建立了消防站的双目标选址模型,并设计遗传算法求解,从而有效地平衡消防站布局安全性与经济性两方面矛盾;曾敏刚等人[3]以总成本最小为目标,建立了应急物资的选址路径优化模型,并对选址与路径两阶段分别用启发式算法予以求解,对提高突发事件的应急管理水平有着重要意义;周骞等人[4]以风险权重、灾害处置难度、建设成本最小为目标,建立了应急物流储备库选址的多目标优化模型,并设计了粒子群算法求解,为解决该类问题提供了决策依据;王旭坪等[5]为解决大规模突发事件发生后黄金救援时间内的应急物资分配问题,以受灾点群众对救援过程时间、需求和效用满意度最大为目标,构建了非线性整数规划模型,并设计了分散搜索算法进行求解,为应急资源分配问题提供了有效的分配方案;陈刚等[6]构建了以物资运达时间和物资运达费用最小、车辆载重利用率最大的上层多目标规划和救援总成本最小的下层规划双层优化模型,并采用自适应遗传算法和 GAMS 软件进行求解;俞武扬[7]在考虑突发事件发生造成应急设施服务能力受损的情况下,以最大加权服务质量期望值为目标建立了选址模型,并设计了基于模拟退火的优化算法进行求解,为应急设施选址提供有益的参考;郑斌等[8]构建了以物资送达时间满意度最大和分配公平性最大为上、下层目标的双层规划模型,设计了混合遗传算法对该模型予以求解,处理了紧急救援过程的物资配送及设施选址决策问题;许可等人[9]建立了考虑物资供应约束以及转运平衡约束的多目标优化模型,设计了带惯性权重的离散二进制粒子群算法对模型进行求解;孙昌玖等[10]建立考虑时间、成本和物资满意度的横向转运应急物资协同调度模型,并采用 NSGA-Ⅱ算法求解该模型;曹策俊等[11]构建了物资送达时间最小化和受灾点群众满意度最大化的双层规划整数模型,并设计了原始-对偶算法对其进行求解,验证了模型的有效性.
应急物资储备库的选址和运输路径规划问题是一个NP-Hard组合优化问题,精确优化算法只能解决相对规模较小的问题,且耗时长,然而现实中这类问题往往是大规模的群体,由于元启发式算法处理许多实际问题时通常可在合理时间内得到满意的可行解,因此可以作为此类问题的优选方案.前述大部分已有研究都是将两个问题分开考虑的,少有将二者作为一个相互影响的整体系统进行研究.此外,对模型也没有一种交互的算法对其进行求解.而选址和调度作为应急物流系统中的两个功能子模块,它们之间相互影响,密不可分.这里,本文针对应急物资调度中心选址与运输路径选择问题,构建了一个选址-调配双层动态交互模型,并设计了基于新型排球超级联赛算法(New Volleyball Premier League Algorithm,NVPL)和改进的遗传算法(Improved Genetic Algorithm,IGA)的混合嵌套算法对模型进行求解,并使用2020年新冠疫情爆发期患病人数数据及全国省市地理位置坐标数据求得了模型较优的可行解.
2 模型建立
2.1 问题描述
在重大疫情和灾害时期,需要在尽可能短的时间内合理安排应急配送中心并以尽可能小的代价将救灾物资在有限运输条件下,选择适当的运输方式尽快运至受灾点并至少满足最低的物资配送时间要求及数量需求.其应急物流系统如图1所示.

图1 灾后应急物流系统示意图Fig.1 Schematic diagram of post-disasteremergency logistics system
中心选址和运输路径规划问题是一个NP-Hard组合优化问题,可以用双层模型来描述:上层模型是在不超过配送中心之间的距离和它与配送的应急转运站规定距离的上限情况下,以尽可能小的时间代价将物资从配送中心运至相应的应急转运站的选址问题;下层模型是在满足配送数量需求的条件下,以较低的时间和运输代价将物资从应急转运站运输到各个应急需求点的车辆路径优化问题,其中,被选为配送中心的应急转运站作为两个模型的连接点.
由于上层的目标属于全局性目标,最优值不仅取决于自身的参数变量、约束条件,还受下层目标值的影响,因此,下层模型须及时将目标值反馈给上层;同时,上层决策也影响着下层模型的路径安排方案.这种反馈机制实现上下层动态交互,进而达到双层模型目标综合最优.
针对该问题特点,可做如下假设:
1)配送中心数量一定,且规模容量总可满足所供应的应急服务转运站需求,并由其配送辐射范围内的需求量确定.
2)各应急转运站和应急需求点只由一辆车配送,且只配送一次.
3)物流运输车辆型号因各需求点的需求量不同而不同.
4)单车运载能力不少于单个需求点的需求量,且每条路线上的需求总量不大于单车最大运载力.
5)所有应急车辆从各应急转运站行驶依次经过所需服务的应急需求点,最终返回应急转运站.
6)车辆配送中的货物尽量在各应急需求点要求的到达时间段内送达,否则将接受时间惩罚.
7)应急转运站及需求点的满意度由软时间窗惩罚费用构成.
8)各配送中心除将物资运输至应急转运站,还给本地区的各应急需求点配送.
9)车辆从应急转运站出发,完成服务后需返回原转运站.
10)各应急转运站和应急需求点的需求量、地理位置已知.
11)各配送中心和应急转运站拥有足够同车型车辆,即能满足需求点的需求.
2.2 符号说明
为方便描述,相关符号定义与说明见表1.
2.3 数学模型
上层是带有时间窗的选址模型,在满足距离上限的情况下,考虑时间窗限制及其他约束条件并附带下层模型的目标,选出最佳的选址方案,进而得到下层模型的各区域最优车辆路径安排.
(1)
(2)
(3)
Mi⊆N
(4)
Zij≤hi
(5)
Djk≤Dmax,∀j,k∈N,j≠k
(6)
dij≤dmax
(7)
(8)
Zij,hi∈{0,1}
(9)
g=minf
(10)

表1 相关变量说明Table 1 Description of related variables
其中,目标函数式(1)表示总的运输代价值最小值,式(2)表示应急转运站j和配送中心i的服务需求分配关系,当其为1时,表示应急转运站点j的需求量由配送中心i供应,否则Zij=0;式(3)规定了被选择为配送中心的数量为p;式(4)表示配送中心i是从应急转运站j中选择;式(5)确保应急转运站的需求量只能被作为配送中心的点供应;式(6)保证了各配送中心之间的距离不超过规定的上限;式(7)保证了应急转运站在配送中心可配送的范围内;式(8)为配送中心将物资配送到应急转运站的时间惩罚成本函数,间接代表需求点的满意度.从应急物流系统的第1阶段特点看,指数形式的时间惩罚函数最符合配送中心将物资运至应急转运站的时间惩罚,即在超出一定时间范围内转运站可接受,但超过某时间范围后将不再接收;式(9)表示Zij和hj是0-1变量;式(10)中g为下层模型目标的最优值.
下层模型是一个带软时间窗的多区域车辆路径问题.按综合道路网络信息,这里用无向完全图U=(I0,L)表示,其中,I0={1,I}为转运站与需求点的集合(1表示转运中心,I={2,3,…,r}表示应急需求点的集合),L={(i′,j′):i′,j′∈I0,i′≠j′}表示车辆行驶路段的集合.
(11)
(12)
(13)
(14)
(15)
(16)
v≤vmax=r
(17)
(18)
(19)

3 双层模型问题求解
上述模型是一个主从复合的交互型双目标模型,第1层目标是全局型目标,即配送中心选址的代价和每个区域的应急转运站配送总代价之和最小;第2层目标是求得各区域转运站配送成本之和达到最小,同时考虑配送距离、单车运输容量、时间窗限制等一系列约束条件.
为求解此模型,本文根据模型特点设计了一个混合嵌套式算法,其中,外层采用NVPL算法,内层利用改进的遗传算法,内外两层不断进行交互反馈,上层目标受下层目标的影响,下层目标又被全局目标指导,最后实现模型结果的综合最优.
3.1 NVPL算法
VPL算法[12]是新的基于种群的优化算法,每个解决方案都是以上场球员形式出现在联赛中,每个球员都想获得最有价值球员称号,每个球队及球员都要使用与排球比赛中有关的程序来更新其位置.使用体育领域中已知的通用框架增强搜索空间中的开发和探索,即在算法中执行各种提升和调节策略.
基于这些更新机制,可使算法的性能得到提高,但由于随机性不足,容易陷入局部最优解.为扩大搜索空间,我们将人类学习算法[13,14]与原VPL算法每场比赛获胜方的训练策略结合(具体见3.1.3小节),在避免算法早熟的同时提高了收敛速度,进而在求解模型第1层时获得较好的可行解.
3.1.1 初始化种群及适应度计算
在新型VPL算法中,每个上场球员代表一个候选解,各球队的上场球员构成初始种群.考虑到每个应急转运站都有一定概率被选作配送中心,故采用随机生成自然数的编码方式.为平衡因种群规模过小陷入局部最优值而种群规模过大又影响算法效率的问题,本文选取种群规模L=60.
将带惩罚项的目标函数式(1)作为上层选址模型的适应度评价函数(见式(20))来评价生成个体的优劣程度,从而可将不满足最大距离限制约束的个体剔除.具体表达式如下:Fit1=∑i∈N∑j∈M(cωjθijdijZij+P(Tij))+g+M,dij≥dmax
(20)
3.1.2 竞赛规程及胜负标准设计
新型VPL算法的每个赛季(迭代)都采用单循环竞赛机制[12,15,16](SSR),即在每个赛季的单循环赛中,所有球队只交手一次,最后根据各队的平均实力排名.
如果联盟中有NT支球队,那么每支球队将进行(NT-1)场比赛.于是,每个赛季共有(N-1)NT/2场比赛.
无论参赛队伍数量是偶数还是单数,都要按双数队伍设置赛程.如果是奇数,可添加序列号为0的团队.
为演示SSR的工作原理,这里列举了一个由8支球队组成的赛程表,如表2所示.

表2 8支球队的赛程表Table 2 Schedule of eight teams

3.1.3 输赢两队赛后调整策略

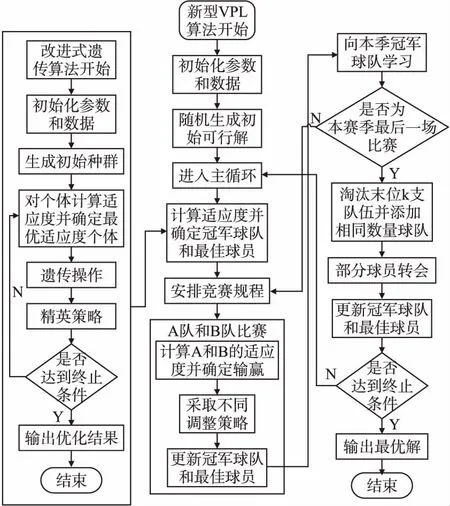
y.F(t+1)=(r′×Pbest(t))+y.F(t),r (21) y.F(t′+1)=r′×(Pbest(t)-y.F(t))+y.F(t),pr≤r≤pi (22) y.F(t+1)=r′×Pbest(t)+y.F(t),r>pi (23) 其中,y.F代表获胜球队上场球员的能力值;Pbest代表联赛最有价值球员;r′、r∈(0,1)内的随机数. 失败队伍x则设计了阶段性策略来提升球员能力.第1阶段的训练方式,见式(24).首先,让球员们找到自身能力与联赛最有价值球员之间的差距并结合自身情况提升自己;若教练认为团队的综合实力已比上一轮比赛对手的能力强,则进行队内互相学习,见式(25),球员之间互相学习对方身上的一些优点;若团队综合实力不如上一轮对手,则采取替补球员上场策略,见式(26). x.F(t+1)=r′×(Pbest(t+1)-x.F(t))+x.F(t) (24) (25) (26) 其中,x.F1(q∶m)表示x队F1球员的某些优点;x.F1、x.S1分别代表x队的上场球员和替补球员;a、b为中间变量. 3.1.4 向本季冠军球队学习 为求得较优的可行解,在下一季比赛之前各队球员都会进行最后的强化训练,其目标是达到这一季冠军球队的实力,具体表达式如下: θ=hmr1=m (27) v=hr2 (28) (29) Xi,j(t+1)=Xbest,j(t)-θ(|vXbest,j(t)-Xbest,j(t)|) (30) 其中,h、α是常数;θ和v是式(29)的系数;T和t分别代表最大迭代次数和当前迭代次数;Xbest,j表示本赛季冠军球队j球员;r1、r2∈(0,1)的随机数. 3.1.5 球队选拔与球员转会 为加快算法收敛速度,在算法后期实施该策略,即,每次季赛结束后,淘汰本赛季末尾k支队伍(k=L×f,其中f为球队淘汰率),并选拔与留下队伍实力相当的球队填补空缺位置.此外,某些队伍的个别球员会在赛末转队.这些操作都会增加种群多样性,进而避免陷入局部最优. 在外层的新型VPL算法生成初始种群后,为求解带时间窗的车辆路径问题,将改进的遗传算法嵌入新型VPL算法中,使得内层算法影响外层算法寻优,同时,外层算法也会指导内层算法寻优,从而实现内外层算法的动态交互. 遗传算法(Genetic Algorithm,GA)最早是由美国的 John Holland于20世纪70年代提出,该算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程来搜索最优解的方法.为增加遗传算法的多样性,避免陷入局部最优,我们在算法的选择操作中设计了一个随机机制,同时在每代遗传操作中采取精英策略[17-19]来影响寻优方向. 3.2.1 编码并计算适应度 这里,我们针对路径规划问题设计了第2层模型.对个体先采用0-1实数编码,设每个区域应急转运站和需要配送的需求点个数总和为q,运输车数量为k,则染色体长度为N=k+q-2.在计算适应度前,需对染色体解码,将转运点用1表示,先将每个区域的转运站和该转运站负责的所有需求点构成一个回路,再将大于k的虚拟节点替换为1,构成多个子回路. 假设某区域转运站和需求点总数为10,则染色体可以表示成S=(1,3,9,6,11,4,7,10,12,5,13,8,2,14). 将大于10的数字都变换成1,则各子回路可以表示为: (1,3,9,6,1)、(1,4,7,10,1)、(1,5,1)、(1,8,2,1). 上述第2层模型是将各个区域调度成本的总和作为解的评价标准,这里将下层目标函数作为适应度函数Fit2,见式(31),适应度值越小的路径方案越优. (31) 3.2.2 随机机制下的路径选择操作 xi(t+1)=xj(t) (32) xi(t+1)=|xb-xi(t)|,∀xb∈X (33) 其中,xj(t)为第t代种群中的任意一个个体xj,xb为前(t-1)代最优个体集合X中的任意一个,r为0-1之间的随机数. 3.2.3 解 码 从各代适应度值最优的个体中找出最优适应度值个体并对该个体进行解码和去重.假设转运中心与需求点数量之和为10,个体A=[0.79 0.97 0.99 0.42 0.27 0.44 0.59 0.78 0.66 0.24 0.88 0.39 0.47 0.86]是具有最优适应度值的个体,其操作步骤如下: 1)解码 依据染色体中的基因数值大小将基因升序排序得到A1. A1=[10 13 14 4 2 5 7 9 8 1 12 3 6 11] 再对解码后的染色体基因进行虚拟节点转换,即将大于转运中心与需求点个数总和的数值替换成1(其中数字1代表转运中心),从而形成多个子回路;然后在染色体A1首尾插入1,得到形成多个子回路的染色体A2. A2=[1 10 1 1 4 2 5 7 9 8 1 1 3 6 1] 2)去重 将A2去重得到A3,即为配送路径的最优方案. A3=[1 10 1 4 2 5 7 9 8 1 3 6 1] 算法步骤及流程图如图2所示. 1)参数初始化:外层-新型VPL算法,种群规模L,迭代次数maxit、淘汰率f、转队率Tr;内层-改进式遗传算法,种群规模nind、迭代次数genmax、交叉率pc、变异率pm以及应急转运中心位置坐标和需求数据等. 2)初始化球员:初始随机生成配送中心点. 3)进入主循环: IGA算法嵌套在外层的新型VPL算法主循环中. (1)编码生成初始路径. (2)遗传操作:首先执行采用随机机制的选择过程,对于父代的优良个体采取精英策略,即将一定比例的父代个体不经过交叉、变异,直接复制到子代种群中;交叉操作过程采用片段交叉的方式,随机选取两个个体,同时随机选取相同的一段进行交叉;变异操作则采用单点变异,根据变异率与随机数的大小决定染色体是否发生变异. (3)执行内层算法迭代,输出最优路径. 4)根据新型VPL算法策略寻找可行解,得到新的种群. 5)迭代终止,输出最优的个体作为最终的配送中心策略和配送路径方案. 图2 算法流程图Fig.2 Algorithm flow chart 全部算法用MATLAB R2019a编程实现,在处理器Intel(R)Core(TM)i5-6200U CPU @2.30GHz,2400 Mhz和4GB内存的计算机上运行通过. 计算实验中的参数设置为:内层-改进式遗传算法,nind=80,genmax=50,pc=0.6,pm=0.05;外层-新型VPL算法,L=60,maxit=100,f=0.5,Tr=0.6. 结合在新冠疫情爆发期(1.28-2.15)丁香园提供的全国各地级市和直辖市城区的确诊病例数据和位置坐标来确定各地的需求量,同时,考虑了各地使用的运输车型不同以及各个需求点对物资的急迫程度不同.在第1阶段设置了在31个省或直辖市中选择6个转运站作为配送中心,各转运站的编号、位置和需求量如表3所示.由于涉及全国各地级市和城区的地理位置、需求量、运输车辆的车型、车速和单次运载能力、配送中心到各转运站的起始时间、卸货时间和转运站到各需求点的开始运输时间、卸货时长等,占用篇幅较大,这里不再一一列出. 表3 各转运站所在区域地理位置及需求量Table 3 Regional geographical location and demand ofeach transfer station 为验证该嵌套式算法探索全局最优解的性能,实验1利用以上数据将双层遗传算法和双层粒子群算法与本文的嵌入式混合算法做对比,并设置相同的最大迭代次数400000,得到表4对比结果;实验2则结合以上数据及本文提出的双层模型和混合嵌套式算法,得到最终配送中心选址策略和各区域向需求点配送物资的路径方案. 表4 两种算法独立运行20次的对比结果Table 4 Comparison results of 20 independent runs of thetwo algorithms 实验1.为了测试本文算法的求解能力,该算例用3种算法独立运行20次,并计算这20次的最优长度、最差长度、平均长度和方差,表3列出了3种算法的对比结果.从最优长度、最差长度以及平均长度数值结果可以看出嵌入式混合算法寻优性能远超于双层遗传算法和双层粒子群算法.且从方差大小得出嵌入式混合算法的优化性能更加稳定.图3给出了这3种算法收敛曲线的对比,同样看到本文提出的算法无论是收敛速度还是求解精度都优于其他两种对比算法.上述实验结果均表明本文算法的寻优性能远超于另外两种对比算法.原因是该嵌入式算法针对每一层模型都有特定的更新策略,比如算法上层的评估学习策略、下层的改进选择操作等来产生新解,进而增强全局搜索能力,避免早熟.同时,该算法采用自适应调整策略来指导决策变量的更新方向,增强了局部搜索能力.本文算法能较好的协调局部搜索和全局搜索,进而表现出较好的优化性能. 图3 算法迭代收敛曲线对比结果Fig.3 Comparison of iterative convergence curve of algorithm 实验2.利用上述提供的数据,结合我们的选址-调配双层模型,采用混合嵌套式算法求解,从而验证本文提出模型的有效性及算法的精确性. 从计算结果可看出,外层选址模型由于考虑到各省或直辖市的需求量及各转运站之间的距离及辐射范围,被选做配送中心的转运站应具备如下一个或多个特点:1)自身需求量相对较大;2)地理位置处于周围应急转运站的相对中心位置;3)转运站负责的需求点相对较多.综合以上3点,并结合目标函数,可选出6个配送中心,分别为4、14、21、22、23和29,如图4所示.由于内层模型为车辆路径规划问题,因此表5列出了全国31个省/直辖市各转运站运输至本地区各需求点的路径规划结果,图5则为部分地区的配送示意图. 图4 配送中心分布结果Fig.4 Distribution center distribution results 表5 计算结果Table 5 Calculation results 续表5 配送中心编号负责配送的转运站编号221->3->1->5->7->1->6->1->2->11->1->4->1->8->1->10->1->9->1231->25->26->17->1->30->33->12->1->16->21->7->19->1->14->36->1->4->1->10->32->1->28->1->3->6->1->22->13->31->27->1->34->1->24->1->29->15->5->1->2->1->11->20->9->18->1->35->23->8->37->1241->11->1->14->1->3->10->1->9->7->1->4->5->1->12->1->8->1->6->2->13->1251->10->1->6->1->2->1->5->11->1->3->1->8->1->4->7->1->9->1261->3->4->5->1->6->7->1->2->1->9->1->8->1271->8->1->6->1->3->4->1->5->1->7->2->9->1281->3->1->8->1->5->13->12->1->7->10->4->1->9->11->2->1->4->1291->8->1->12->7->1->10->9->5->1->6->2->1->11->3->13->1->4->1301->3->1->8->1->7->13->15->1->17->1->12->2->1->14->1->15->16->1->4->10->1->19->1->18->20->6->1->11->9->1311->14->11->7->1->10->3->5->1->4->13->8->12->6->9->1->2->1上层目标值4.44E+06 从计算结果可知,由于考虑到运输成本、时间成本、单次运载能力等条件限制,同时由于下层目标受上层目标的影响,各转运站的路径规划方案未必都是最优,但最终达到了双层模型综合目标最优. 图5 某些区域的车辆路径安排结果Fig.5 Results of vehicle routing in some areas 本文针对应急物流系统中的规模选址与路径规划问题,构建了一个上下层动态交互、互相影响、彼此牵制的选址-调配双层模型,从而实现上下层目标的综合最优.设计了一种混合嵌套算法对模型进行求解,其上层采用离散的新型VPL算法,下层利用改进的遗传算法求解.以丁香园提供的全国各地级市和直辖市城区的确诊病例数据和位置坐标,通过对其路网和需求数据分析计算,并采用我们的双层模型及其算法,获得了有益的结果.后续的研究,将聚焦需求不确定下的应急救援中心的选址-调度模型及其算法设计.

3.2 改进的遗传算法
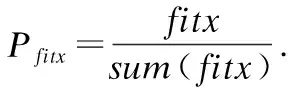
3.3 算法步骤
4 算例分析
4.1 参数设置及实验环境
4.2 实验结果与分析







5 结 语

