基于全站扫描仪的真配对点形变计算及点面优化
吴金波 张晓春 杨聃 朱悦林 陈俊涛 苏凯







摘要:水电站厂房内设备传统变形监测采用点测量方式,无法反映整体变形特征,而全站扫描仪可快速采集目标表面点云,通过点云处理得到形变量。基于全站扫描仪提出了真配对点的形变计算方法,根据后方交会法设计方案,采集两期点云数据,然后基于真配对点计算形变量并通过点面优化算法减少误差,最后验证了形变计算方法的精度。设计了两个模拟试验验证算法的可行性,通过细绳模拟输电线路弧垂变形和箱体外加锥体模拟壳体鼓包变形,在试验对象上施加外力使其产生形变,并精确测量形变量作为形变参考值。试验结果表明:两个模拟试验的形变计算误差分别为0.146 mm和0.056 mm,精度可达亚毫米级。该形变计算方法能够较好地应用于设施设备变形监测领域。
关键词:形变计算; 全站扫描仪; 后方交会法; 孤立点云选取
中图法分类号:TV698.1 文献标志码:A DOI:10.15974/j.cnki.slsdkb.2022.01.006
文章编号:1006 - 0081(2022)01 - 0029 - 08
0 引 言
传统的变形监测是以点测量技术为主,采用水准仪、全站仪等仪器测定监测点的三维坐标,然后利用坐标值进行形变量的计算和分析[1]。近年来,随着三维激光扫描技术的发展,国内外学者开始用三维激光扫描仪进行变形监测研究。Zhou 等[2]通过地面三维激光扫描仪获取点云数据,建立数字高程模型相减得到矿区地表动态沉降量。梅文胜等[3]对某铁路经过区域进行外业作业,通过后处理软件进行地物和地貌提取,绘制等高线地形图。卢秀山等[4]运用车载式激光扫描仪和CCD相机获取城市信息,提取建筑物特征实现三维模型重建。谢雄耀等[5]对上海地区服役电力塔进行三维激光扫描监测,通过拟合铁塔点云轴线判断其倾斜度。刘求龙等[6]利用地面三维激光扫描仪获取惠泉变电站的空间数据,建立三维空间可视化模型,提供了三维激光扫描仪运用于变电站的新思路。HASAN 等[7]使用三维激光扫描技术对水工建筑物的混凝土表面磨损和体积损失进行分析。
三维激光扫描仪可以非接触式扫描得到点云数据,但测距测角精度没有全站仪高,且每站扫描为独立坐标系,在实际应用中会造成不便。而全站扫描仪集成了多项先进的测量技术,是近年来的一项重要技术革新[8]。全站扫描仪可以进行传统的全站仪测量和三维扫描测量,不仅能获取高精度的单点坐标以计算目标的刚体位移,还能获取目标的点云数据,计算局部形变量[9]。相较于三维激光扫描仪,全站扫描仪具有更高的精度,可定点并用后方交会法设站,在同一坐标系下进行扫描,无需点云拼接,避免复杂的数据配准工作[10]。全站扫描仪无需布设监测点,在水电站厂房中部分设备的运行期间不允许工作人员接近、无法在设备上布设监测点的情况下,非接触测量技术可在远离目标处通过线扫描获取点云数据,实现安全高效的非接触测量。
对水电站厂房内设备进行变形监测,在形变预警前采取控制措施以避免设备故障影响生产工作,保证水电站发出的电能通过输电线路并入电网,具有重要而深远的意义。为验证本文算法的可行性,设计了两个试验模拟重要设备的常见变形:试验一模拟覆冰荷载、风荷载等常见荷载对输电线路的影响;试验二模拟内部过电压对主变压器的影响,以此验证算法精度。
1 研究方案
本文拟采集两期全站扫描仪数据进行形变分析。初始点云数据中存在噪声点,对形变量计算产生干扰,影响试验精度。首先,需要对采集到的点云数据进行预处理,通过人机交互和基于投影的点云去噪算法剔除噪声点。然后,针对去噪后的多期点云数据,通过点与点之间的最小距离选择真配对点,先以真配对点之间的距离计算形变量,再运用优化算法减少误差,提高形变量计算的准确性,输出形变结果。具体技术路线图如图1所示。
2 点云数据获取及去噪
2.1 点云数据获取
全站扫描仪主要是运用“后视点+测站点”的采集方式,兼具普通全站仪和扫描仪的功能,因此全站扫描仪获取点云数据无需进行配准。扫描目标前,应围绕扫描目标规划好测站点和棱镜位置,如图2所示。因需要获取两期点云数据来计算形变量,并且要保证两期点云的坐标系统一致,所以兩期点云扫描时的测站点和棱镜位置也应相同。每期点云数据获取工作步骤如下:
(1) 在测站点1位置放置全站扫描仪,并对中整平,设置为初始测站坐标(X0,Y0,Z0)。应尽量让仪器能够扫描到目标整体,并在视野开阔位置设置3个后视点放置棱镜。
(2) 完成测站点1的初始设站后,选择棱镜1作为标准方向,通过全站扫描仪的“测量”模式测量仪器到每个棱镜的距离、水平角和竖直角,以此计算棱镜的三维坐标(Xi,Yi,Zi)(i=1,2,…),获取多个已知点来确定测量坐标系统。
(3) 对目标进行扫描,得到本站点能观测到的部分目标点云数据。
(4) 初始测站观测完成后,搬至规划的测站点2,通过步骤(2)得到的棱镜坐标和后方交会法得到测站点2的三维坐标,然后在测站点2建站,并在此站点以新的观测角度扫描目标。
后方交会法是利用测站点2位置测量仪器到已知棱镜点的距离、水平角和竖直角,以此计算新站点的三维坐标(X,Y,Z)。点云数据获取及后方交会法示意见图2。图2中,初始测站(X0,Y0,Z0)、棱镜点(Xi,Yi,Zi)、新站点(X,Y,Z)都在同一个坐标系内。此方法可在合适的点设站,并计算同一个测量坐标系下任意新站点的三维坐标,进行点云采集及处理,无需数据配准。
2.2 噪声点去除
在扫描获取点云数据的过程中,由于仪器误差、扫描区域过大、被测物体表面差异引起反射不同、边缘效应等原因,产生冗余点即点云噪声[11]。而噪声点的存在会对后续的点云处理和三维建模过程造成一定影响。所以,要对初始点云数据进行去噪。本文采取人机交互和基于投影的去噪算法分别进行粗去噪和细去噪,消除噪声点的干扰。
2.2.1 基于人机交互的粗去噪
针对可肉眼辨别的非目标点云,可直接在点云模型中,通过人机交互的方式,选中并删除噪声点。手动框选时,应尽可能做到细致、谨慎,避免错误删除目标主体点云。对于偏离目标主体点云的浮游噪声点,也可以通过孤立点云的选取算法选中后剔除,如图3所示。孤立点云选取算法的原理是首先设定一个距离阈值和最大选取点云数量,例如,图3中距离阈值为r,取值一般小于20 cm。本文通过计算点云中两点之间的距离,排序后以1 cm为划分区间,统计各区间中点云数量最多的两个,求平均值得到r=5.5 cm。然后,由主体点云中的初始中心点向外搜索半径为r的范围。图3中1号点为初始中心点,其搜索范围内有2,3,6号点,再以2,3,6号点作为下一次搜索的中心点进行半径为r的搜索,直至没有新的点可以被覆盖或点云数量已达到最大值时停止。剩余点云作为浮游噪声点予以去除,如图3中的9,10号点。
2.2.2 基于投影的点云精细去噪
在初步完成人机交互去除非目标点后,运用基于投影的点云去噪算法,精细去除噪声点,如图4所示。首先,定义一个邻域的概念,任意点A的邻域是以A为中心构建边长为2r的正方体内所有的点,r的大小由选定的邻域内点的数量决定。图4中黑色实心点为邻域内的点,空心点为邻域外的点。然后,对邻域内点集进行面拟合计算,对不同的邻域点集可采取不同的拟合面类型。一般可拟合为普通平面、柱面、二次曲面等,图4中采用的拟合面为普通平面。一般的拟合函数可用最小二乘法来计算求解。最后,将该点集中的点投影到拟合面上,设定偏移阈值,超出偏移阈值的点予以删除,符合偏移阈值的点将偏移至拟合面。为了提高去噪的精度,对初次拟合、投影后的点重复上述过程,多次迭代投影,完成精细去噪。邻域内点坐标集合:
[{P(x, y, z)|xa-r≤x≤xa+r, ya-r≤y≤ya+]
[r, za-r≤z≤za+r}] (1)
式中:P為属于邻域内的点,r为邻域正方体边长的一半,邻域中心A的坐标为(Xa,Ya,Za)。
3 基于点云真配对点的模拟形变计算模型
3.1 形变计算
对两期点云进行了粗、细去噪后,依据点云数据计算两期点云模型的形变量。但由于点云数据的不可重复性,两次点云的采集过程不会完全按照相同的顺序进行扫描,两次采集的点数量也无法完全相同,无法直接找出两期点云中一一对应的实际对应点。有学者提出了一种基于特征点控制区域点云形变方向的方法,得到在重建模型上的虚拟对应点[12]。但是水电站厂房部分设备运行期间不允许人员靠近,更无法在待测点贴反射片作为特征点来控制区域点云形变方向得到对应点。本文首先采用最邻近点算法选取真实配对点,然后基于点面距离优化法计算形变量。点云模型形变计算具体步骤如下。
3.1.1 基于点点距离的真配对点选取
为计算点云模型的形变量,首先考虑把点云看作大量点坐标的集合,通过两期点云中对应点的欧几里得距离得到单点形变量:
[D=(X2-X1)2+(Y2-Y1)2+(Z2-Z1)2] (2)
式中:第一、二期点云中对应点的三维坐标分别为(X1,Y1,Z1),(X2,Y2,Z2)。
然而,第二期扫描的点云不一定包括第一期的所有点,因此无法直接找出所有的对应点,并很难通过欧几里得距离公式计算单点形变量。因此,本文通过选取真配对点的方式来获取一一对应点,如图5所示。选择第一期点云中的任意一点与第二期点云中每一个点进行配对,计算欧几里得距离,选择最小距离(最邻近点)作为真配对点。遍历第一期的每一个点,完成所有真配对点的选取。如图5所示,其中D1为最小距离,所以D1两端的点为真配对点,真配对点选取对应公式为
D=min{D1,D2,D3,…,Dn} (3)
3.1.2 基于点面距离优化法的形变量计算
在工程实际中,扫描观测目标的真实形变不会是单点的位移,而是由点控制的一个区域的连续形变,在区域中各点的位移相互关联。在实际数学模型中,最邻近点的欧几里得距离并不一定是点云模型的真实形变量,如图6所示。它们之间存在误差,需要通过设计优化算法,将误差调整到允许范围。
本文的优化算法为对第一期点云中的任一点P,在第二期点云中通过上述方法选择其最邻近点。然后在最邻近点的几个相邻点间进行局部建模,拟合三角面片,计算点到三角面片的距离最小值。相邻点数量过少,无法达到优化效果;相邻点的数量过多,则计算量大大增加,计算效率降低。本文的两个模拟试验中点云数量在25万到40万之间。当选择相邻点数量大于等于7时,无法完成计算,所以选择6个相邻点进行三角面片拟合。由点点的距离改进为点面的距离,以此替换最邻近点距离。如图7所示,实线为计算距离,虚线为真实距离。经优化后减少了误差,在统计上更加精确。拟合三角面片的平面方程如下:
Ax+By+Cz+D=0
式中:A,B,C,D为常数;x,y,z是平面上点的坐标。
点到平面的距离计算公式:
[d=Ax1+By1+Cz1+DA2+B2+C2] (4)
式中:(x1,y1,z1)为平面外一点的坐标。
3.2 精度计算方法
本文是基于两期点云的真配对点选取及优化算法来减少误差。影响试验精度的因素主要包括仪器自身的扫描精度及偏心误差、三角面片建模误差等,这些因素相互独立,则形变误差Δ为
Δ=Δ仪器+Δ模+Δ其他 (5)
但目前对模型重建的精度分析缺少统一的评价标准,不能为重建模型提供较为准确的精度估计值,因此很难通过误差计算公式直接评价形变计算的精度[13-14]。本文通过设计模拟变形试验,选取精度远高于目标精度的千分尺获取形变参考值D参,作为评价方法精度的形变真值,与本文提供算法计算得到的形变量D算进行对比,并以下式(6)得到形变量计算误差D,验证该方法在形变监测中的可行性。
[D=D参-D算] (6)
4 试验及精度分析
4.1 试验设备及设计
基于Leica MS50全站扫描仪采集点云数据。MS50采用波形数字化的测距原理,是传统相位法和脉冲法的融合,它同时具有相位法光斑小、精度高、测量范围远的优点和脉冲法的快速测距特点,较好地弥补了两种方法的不足。相较于传统方法,在确保测距精度的条件下,测量效率提高约50%,测程可达10 000 m。该方法扫描原理为采用线扫描,马达驱动望远镜先上下摆动,根据设定的竖向点间距采集点云数据,单线采集完毕后,再水平移动预设的横向点间距,重复线扫描。MS50是基于全站仪设站定向的方法进行扫描的,点云数据已统一到同一独立坐标系,无需进行坐标转换拼接[15]。
根据SL 511-2011《水利水电工程机电设计技术规范》,为保证水利水电工程的安全稳定运行,水电厂电气主接线应满足稳定性、可靠性的要求,并结合考虑枢纽总体布置、地形和设备特点等因素[16]。水电站输电线路常在覆冰荷载、风荷载的作用下产生变形,影响水电站电能输送。覆冰可能会导致铁塔两侧的导线产生纵向不平衡张力,导线悬垂高度变化及铁塔拉、压破坏[17]。风荷载使导线舞动,舞动幅度过大则会导致铁塔的直接损伤,严重威胁输电线路的安全运行[18]。水电站主變压器和高压配电装置在系统发生电路故障时,或恶劣天气条件下可能会产生壳体变形。当发生线性谐振过电压时,会造成绝缘击穿,导致内部气压增加而出现壳体鼓包。
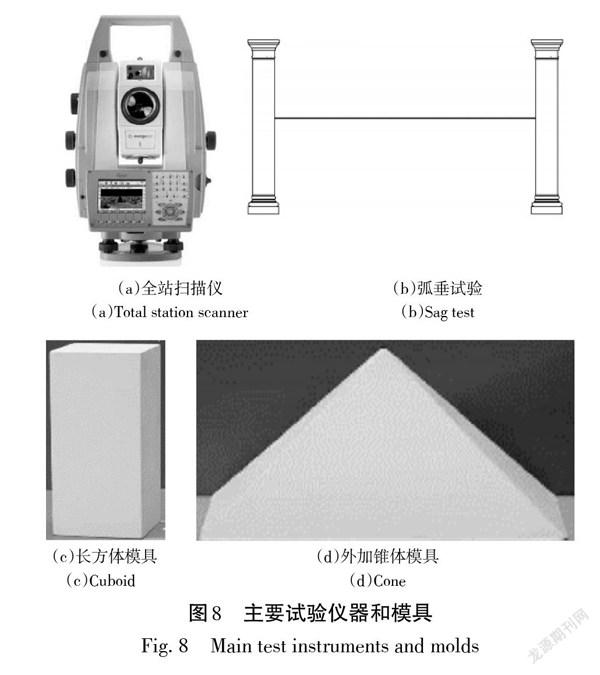
根据《水利水电工程机电设计技术规范》和工作人员提供的水电站厂房内设备的常见变形情况,本文将设计试验模拟输电线路受冰雪荷载、风荷载的弧垂变形和变压器内部过电压产生的壳体鼓包变形,通过精度高于全站扫描仪测量精度的千分尺测量得到形变参考值,与本文算法得到的计算值进行比较,验证精度。主要试验仪器和模具如图8所示。
4.2 试验方法
4.2.1 试验一:输电线路弧垂变形试验
试验一是用固定在两柱之间的绳子模拟电线杆之间的输电线路,用绳子由水平到中心略微悬垂模拟冰雪荷载和风荷载作用下舞动造成输电线路弧垂变化。通过保持两端点位置固定,将两端点内绳子长度增加使其中心自然下降一定距离,通过精度可达1 μm的千分尺测量得到绳子中心下降前后的距离,得到最大参考形变量。
首先在选定两柱水平对应位置绑上绳子,调整长度使其绷直。选择一个位置作为初始测站点安置全站扫描仪,进行对中整平。在目标周围设立棱镜作为后视点,选用“测量”模式采集棱镜的三维坐标。选用全站扫描仪“测量+”模式对目标进行三维激光扫描,扫描完毕后搬站。以后方交会法计算新站点的设站坐标,使得每一站都在同一个坐标系下,再对目标进行三维激光扫描。多次搬站使得点云扫描范围包含目标的各个角度,第一期扫描完成得到相应的目标点云数据。点云扫描示意如图9所示。
固定端点位置,调整绳子长度,使其悬吊,静待一段时间直至绳子不再晃动且绳子中心下降距离稳定。然后,重复上述设站扫描过程,得到第二期点云数据。根据本文提出的形变计算方法对两期点云进行形变计算,并和用千分尺测量得到的形变参考值比较验证精度。图10(a)中红色线为第一期绳的点云,其他白色部分为第二期点云。
4.2.2 试验二:壳体鼓包变形试验
试验二是采用在原始目标上外加锥体来模拟过电压、过电流引起的设备壳体鼓包形变。如图8(c)所示的长方体为第一期扫描对象,图8(d)为第二期外加锥体,用以模拟水电站厂房设备由于内部绝缘击穿引起的壳体鼓包变形。首先,进行第一期点云扫描,即仅扫描原始长方体,用以模拟设备未发生形变的状态。选定初始测站点,放置棱镜作为后视点,在初始测站点建站,通过“测量”模式采集棱镜的三维坐标;然后,运用“测量+”模式扫描原始长方体。扫描完成后搬站并用后方交会法计算得到在同一坐标系下新站点的三维坐标,再次对目标进行扫描。整个扫描过程应使目标能够被完整扫描,并且固定长方体位置,避免在水平方向上移动。之后进行第二期点云扫描,即在长方体上表面外加锥体进行扫描,用以模拟设备上表面的鼓包变形,重复以上扫描过程。最后,对比两期点云计算形变量,并与参考值进行比较分析。参考值是通过千分尺测量锥顶到锥底的垂直距离,即为最大参考形变量。图10(b)白色部分为第二期点云,其中红色框内为第二期外加锥体的点云。
4.3 试验结果与精度分析
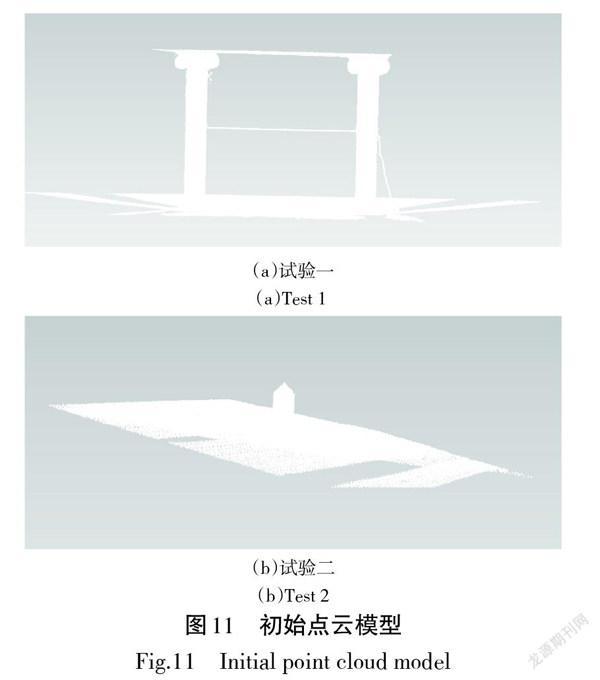
首先,导入全站扫描仪多站点测得的点云数据,初始点云模型如图11所示。
以试验一第一期点云为例,为消除噪声点的影响,先基于人机交互粗去噪,选中并去除肉眼可见的地面点云。对于偏离目标主体点云的浮游噪声点,则通过孤立点云的选取算法选中后剔除,首先计算点云模型中两点之间的距离,将计算得到的所有点对距离排序后以1 cm为划分区间,统计各区间中点云数量,选择点云数量最多的两个区间,求平均值得到r=5.5 cm。未去噪前点云数量为41万,经估算,目标主体点云应在35万以内,所以设置距离阈值r=5.5 cm,最大选取点云数量N=35 0000个进行孤立点云选取,选中后删除浮游噪声点。试验二设置距离阈值r=1.5 cm,最大选取点云数量N=10 000个。
對去噪完成后的点云进行真配对点选取,选择变形前的第一期点云中的某一点P,运用欧几里得距离公式计算其与第二期点云中每一个点的三维距离Di,用最小值函数比较得到距离的最小值,最小距离对应的第二期点云中的点P*即为真配对点。为提高精度,实现由单点控制的一个区域内的连续变形测量,对P*及其周围的6个相邻点分别进行三角面片拟合,并计算P到这些三角面片的点面距离,取点面距离的最小值为计算结果。将上述过程遍历两个试验的第一期点云,形变计算的最大值为验证形变误差的计算形变量D算。完成预处理后的点云模型如图11所示。
基于本文提出的两期点云真配对点选取和优化算法,计算形变量。两个试验用千分尺测得的形变参考值D参和基于本文算法优化后得到计算形变量D算如下表1所示,由式(6)计算得到形变量计算误差。
由表1可看出,基于两期点云真配对点形变量的计算误差均小于0.250 mm,满足水电站厂房设备变形监测的毫米级要求。试验结果表明,本文提出的搜索真配对点,将点面之间的最小距离作为形变计算结果的方法,具有较高的计算精度。
5 结 论
本文针对水电站厂房设备的变形监测,提出基于真配对点的形变计算方法,并设计了模拟设备变形的试验,根据试验结果得出以下结论:
(1) 传统变形监测只能采取单点测量和接触式测量,基于全站扫描仪的变形监测具有面测量及非接触式测量等优势。
(2) 基于本文监测方法可以满足非接触测量要求,即不需在观测目标上标定特征点,通过选取真配对点计算形变量,利用点面距离优化算法减少误差。
(3) 本文设计了两个变形模拟试验,对水电站厂房输电线路弧垂变形和壳体鼓包变形进行模拟,将计算形变量和形变参考值进行比较,验证方法精度。
(4) 试验计算结果与参考值之间误差小于0.250 mm,达到亚毫米级精度要求,验证了本文计算方法的可行性和可靠性。
参考文献:
[1] 刘备. 电力工程变形监测数据处理分析与系统实现[D]. 青岛:山东科技大学,2018.
[2] ZHOU D, WU K, CHEN R, et al. GPS/terrestrial 3D laser scanner combined monitoring technology for coal mining subsidence: a case study of a coal mining area in Hebei, China[J]. Natural Hazards,2014,70(2):1197-1208.
[3] 梅文胜,周燕芳,周俊. 基于地面三维激光扫描的精细地形测绘[J]. 测绘通报,2010(1):53-56.
[4] 卢秀山,李清泉,冯文灏,等. 车载式城市信息采集与三维建模系统[J]. 武汉大学学报(工学版),2003(3):76-80.
[5] 谢雄耀,姜毅,卢晓智,等. 超高压服役杆塔病害及三维激光扫描检测技术[J]. 地下空间与工程学报,2014,10(3):668-674.
[6] 刘求龙,胡伍生,王骢,等. 三维激光扫描仪在惠泉变电站三维模型构建中的应用[J]. 测绘科学,2011,36(2):210-212.
[7] HASAN M S, LI S S, ZSAKI A M, et al. Measurement of abrasion on concrete surfaces with 3D Scanning technology[J]. Journal of Materials in Civil Engineering, 2019, 31(10):04019207-1-8.
[8] 李东敏,范百兴,周蕴,等. 全站式扫描仪测量原理及精度分析[J]. 测绘通报,2014(8):131-133.
[9] 汪冲. 全站扫描仪测量精度分析及其在变形监测中的应用[D]. 郑州:中国人民解放军战略支援部队信息工程大学,2018.
[10] 张教权,左美蓉,喻艳梅. 施工测量中后方交会法的应用[J]. 科技创新导报,2010(22):44-45.
[11] 刘静静. 三维点云重建中的去噪算法研究[D]. 北京:北京交通大学,2019.
[12] 汪冲,范百兴,皮刚,等. 一种基于全站扫描的特征点自约束点云变形分析方法[J]. 测绘通报,2019(1):44-49.
[13] 李德仁,袁修孝. 误差处理与可靠性理论[M]. 武汉:武汉大学出版社,2002.
[14] 隋立芬,宋力杰,柴洪洲. 误差理论与测量平差基础[M]. 北京:测绘出版社,2010.
[15] 朱晓康,邹进贵. MS50全站扫描仪性能研究[J]. 测绘通报,2015(增1):114-118,128.
[16] SL 511-2011 水利水电工程机电设计技术规范[S].
[17] 杨靖波,李正,杨风利,等. 2008年电网冰灾覆冰及倒塔特征分析[J]. 电网与水力发电进展,2008(4):4-8.
[18] 李勇杰,韩纪层,何成,等. 强风区750 kV超高压输电线路引流线断股机理研究[J]. 武汉大学学报(工学版),2020,53(10):923-931.
(编辑:李 慧)
Deformation calculation of true pair points and optimization of points and surfaces based on total station scanner
WU Jinbo1, ZHANG Xiaochun1, YANG Dan2, ZHU Yuelin2, CHEN Juntao1, SU Kai1
(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China; 2. Jinshuitan Hydropower Plant, State Grid Zhejiang Electric Power Co., Ltd., Lishui 323000, China)
Abstract: The traditional deformation monitoring of equipment in hydropower plants uses point measurement, which cannot reflect the overall deformation characteristics. However, the total station scanner can quickly collect the target surface point cloud, and obtain the shape variable through point cloud processing. Based on the total station scanner, the deformation calculation method of the true paired point was proposed. According to the design plan of the rear intersection method, the two-phase point cloud data was collected, and then the deformation was calculated based on the true paired point and the error was reduced by the point and surface optimization algorithm, which has verified the accuracy of the deformation calculation method. Two simulation experiments were designed to verify the feasibility of the algorithm. The sag deformation of the transmission line and the bulging deformation of the case were simulated by adding a cone outside the box. The external force was applied to the test object to produce deformation, and the deformation was accurately measured as a reference value for deformation. The test results showed that the deformation calculation errors of the two simulation tests were 0.146 mm and 0.056 mm, respectively, and the accuracy can reach sub-millimeter level. Therefore, the deformation calculation method can be better applied to the field of facility equipment deformation monitoring.
Key words: deformation calculation; total station scanner; rear intersection method; isolated point cloud selection

