盾构下穿施工中土体损失和左右线施工间距对站房变形影响的数值模拟

沙俊玲，刘 洋，刘旭鹏，王 磊，刘志涛

(1.安徽建筑大学 建筑结构与地下工程安徽省重点实验室，安徽 合肥 230601；2.安徽建筑大学 安徽省城市建设和地下空间工程技术研究中心，安徽 合肥 230601；3.中铁隧道局集团路桥工程有限公司，天津 300300)

为缓解地面交通压力，实现快速分流，在地铁建设过程中主要以下穿城市主干道和人口聚集地为主，这就不可避免的需要盾构穿越火车站站房等高风险建筑。在盾构施工过程中会对隧道周围土体进行卸载和重新注浆加压等过程，打破地层原有的应力平衡，引起隧道周围土体扰动和变形[1]，进而诱发地表发生不均匀沉降和上部结构变形。为减小盾构施工过程对于周围土体的扰动，保证上部建筑物的安全[2]，需对盾构过程中的掌子面压力、左右线前后施工间距、注浆压力等因素进行严格控制。并且在盾构掘进过程中，由于盾构施工暂停、盾尾注浆不及时以及小半径盾构推进导致超挖等因素都会使得盾构隧道挖土体积要大于实际建成隧道体积，它两之差被称为土体损失[3]。盾构土体损失是引起地表发生沉降变形的主要因素之一[4-5]，我们通常用土体损失率来表示，即单位土体损失体积和单位盾构隧道体积之比[6]。因此对于盾构施工影响因素的控制量分析具有较大意义。

杨潇[7]基于地层损失，并根据土体极限平衡原理和隧道周围统一土体移动模型得出盾构掘进土体变形修正Loganathan公式。魏纲[8]在考虑多因素情况下所造成土体变形对于土体水平位移的影响，得出盾构隧道周围土体的水平位移主要由土体损失引起的。王建秀[9]以地层损失为介质，建立盾构参数与预测地表沉降的关系，以达到控制地表沉降的目的。吴锋波[10]收集了大量在建项目，统计分析了软土、黏性土、砂卵石地层、风化岩层以及黄土等的双线隧道地层损失率平均值和标准差，为预测隧道开挖影响范围和施工提供科学依据。丁智[11]基于半无限饱和土的初值解结合相关算例，考虑了隧道先行和后行不同位置对土体扰动的影响，得出平行隧道间距越小，二次扰动越明显。欧孝夺[12]基于Peck公式的基础上，研究双线隧道相互影响，并引入左右线影响系数，从而提出一种盾构开挖引起地表沉降预测模型。

由于目前国内外学者对于左右线盾构施工间距影响地表沉降和建筑物变形的研究较少，本文以合肥一号线盾构下穿合肥火车站为背景，利用Plaxis3D软件进行双线隧道相隔不同掘进环数以及用隧道收缩模拟不同地层损失率等不同工况下对站房底板变形、地表沉降进行模拟分析。

1 工程概况和工程控制标准

1.1 工程概况

合肥一号线三期工程合肥站-瑶海公园站区间，全长采用地下盾构法施工，其下穿合肥站房是1号线三期工程的控制节点。

合肥站站房为2层框架混凝土结构，底板下基础为独立基础和混凝土灌注桩，独立基础底标高为23.75m，桩径为1m，桩长7.1m，桩底标高为21.75m。区间隧道正穿火车站站房与隧道位置关系如图1所示，盾构隧道顶距独立基础底约5.683～8.135m，盾构隧道顶距人工挖孔桩底6.153m。

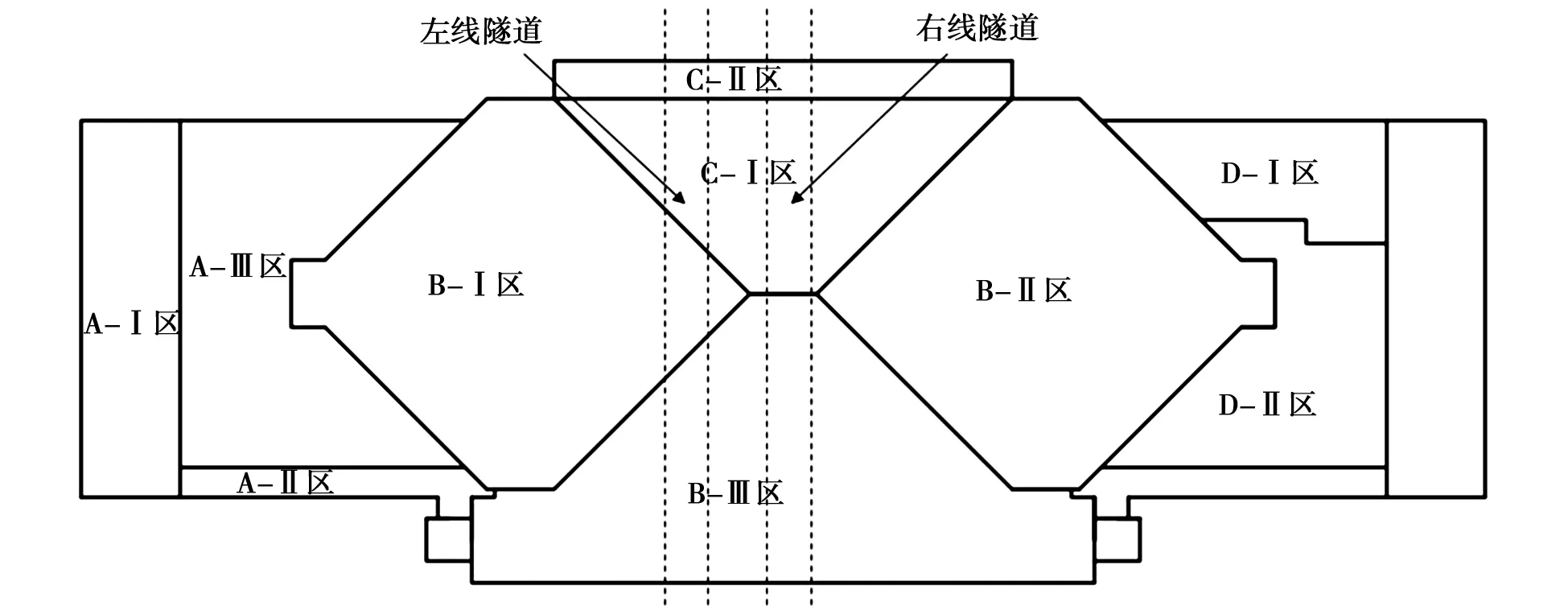
图1 站房与隧道位置关系图

该项目所采用的盾构机为土压平衡盾构机，并进行双线开挖掘进，盾构隧道直径6m，左右线隧道中心间距15m。

合肥火车站地层分布主要是如图2所示，以杂填土、黏土以及砂岩为主，其中黏土层主要是第四系全新世冲洪积层和第四系晚更新世冲洪积层，并且其含有铁锰结核及灰白色高岭土。

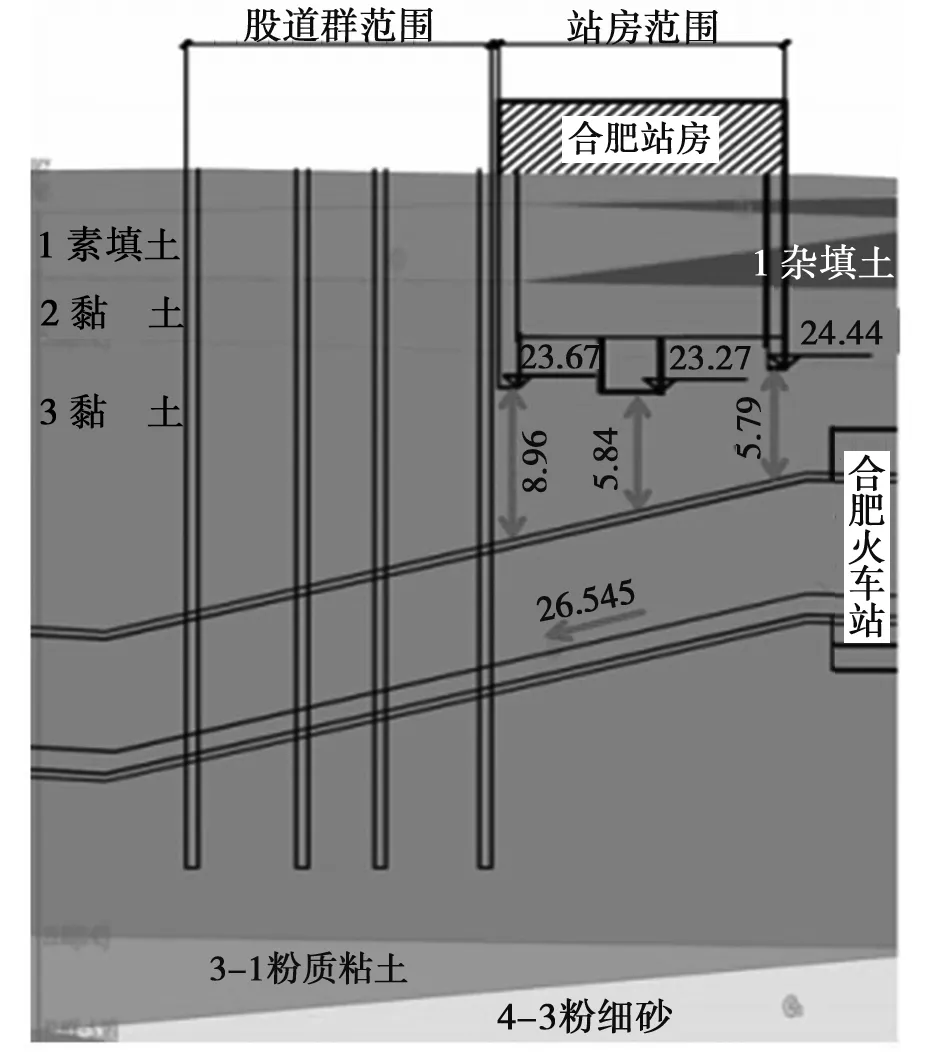
图2 站房地层分布剖面图

1.2 工程控制标准

根据CJJ/T 202-2013《城市轨道交通结构安全保护技术规范》[13]以及合肥市黏性土层施工的相关经验得出合肥站站房变形严格控制标准如表1所示。

表1 合肥站房变形控制标准

2 模型建立

2.1 数值模型和计算参数

本模型双线隧道内直径6m，管片厚度0.3m，掘进总长度约90m，左右线隧道轴心距15m，隧道中心埋深约18m，独立基础长宽高为2.4m×2.4m×3m。

建立的土体三维模型尺寸为300m×100m×50m，土体采用摩尔库伦模型，该模型以一环管片长度为一个施工步骤(每环管片长度为1.5m)，单个隧道模拟60环施工管片，三维计算模型如图3所示。

图3 模型立面图

结构单元采用实体模型，站房现浇注底板和盾构管片采用板单元模拟，站房立柱采用点对点锚杆模拟，为充分贴近实际，采用线弹性单元模拟站房下的基础。相关地层物理性质参数如表2和表3所示。

表2 地层参数

表3 结构参数

2.2 模拟因素及工况选取

(1)由于合肥火车站的特殊性，其每天的人员流通量巨大，对于盾构施工工期要求在保证安全的情况下，尽可能的压缩工期。所以模拟左右线相隔不同掘进环数(相隔环数为10、20、40、60环)，并分析其对于地表沉降和站房变形的影响，在保证施工安全的情况下，尽可能的缩短施工工期，予以实际工程指导。

(2)赵坤[14]对于合肥地区地层主要为黏土和软岩地层，盾构施工产生的地层损失率范围取0.2%～1.0%。所以该模型取地层损失率为0.2%、0.4%、0.6%、0.8%、1.0%等进行模拟。

(3)模型按照实际工程进行分工况分析，如表4所示，主要分为3个施工工况，初始工况是在已建成的新旧拼接而成的车站情况下，土体地层经过长时间固结沉降形成较为稳定的初始地应力场，第二工况和第三工况主要是开始进行盾构左、右线的开挖，在开挖过程中主要是盾构隧道周围土体产生扰动，然后再次达到应力平衡状态，主要模拟在盾构过程中隧道开挖、管片安装、盾尾注浆以及盾构隧道收缩等过程。

表4 工况叙述

3 模拟结果分析

3.1 不同地层损失率对地表沉降影响

3.1.1 地层损失率理论分析

Peck[15]认为在不考虑土体的固结排水作用下，盾构隧道掘进引起地面沉降的体积与地层土体损失相等，其横向地表沉降经验公式为：

(1)

由公式(1)可知横向地表沉降经验公式主要取决于沉降槽和土体损失量的大小，公式(2)为沉降槽宽度，公式(3)为土体损失量。

(2)

Vi=V1πR2

(3)

式中：S(x)—距离隧道轴心为x的地面沉降量/m；

Smax—隧道轴线上方隧道最大沉降量/m；

i—地面沉降槽宽度/m；

Vi—盾构隧道单位长度地层损失量/(m3/m)；

V1—地层损失率；

H—隧道轴线上覆土厚度/m；

r—隧道半径/m；

R—隧道外径/m；

φ—各土层内摩擦角加权平均/(∘ )。

可由公式(1)、(2)、(3)得出地表最大沉降量与地层损失率的关系为：

(4)

由公式(4)可知，影响地表最大沉降量因素有很多，如隧道半径、覆土层厚度、土层内摩擦角以及土体损失率等，在一定的项目中，隧道相关参数为确定量，如图4中曲线所示，地表最大沉降量与土体损失率成正比关系，且由Peck公式推演得出，其正相关系数一定。并在图4理论数据与模拟数据Smax与V1关系对比图中可看出，模拟出的数据离散分布在理论曲线附近，表明模拟与理论相符合。

图4 理论数据和模拟数据Smax与V1关系比对图

3.1.2 模拟分析

由图5可知在双线隧道间距15m时，对于隧道半径为3m的地表沉降为“W”型沉降槽，当模拟土体损失增大时，地表最大沉降量也同时增大，并且可看出当双线隧道间距保持不变时，随着土体损失的增大，两隧道对中间区域影响就越明显，其表征是隧道中间的沉降在不断发生改变，当土体损失足够大时，其地表将会形成“V”型沉降槽。

如图5所示，当土体损失率达到0.4%时，地表最大沉降量达到3.74mm，土体损失达到0.6%时，地表最大沉降量达到6.31mm，为保证地表结构安全以及符合相应规范，应控制土体损失率在0.4%左右较好。

图5 不同土体损失下沉降图

3.2 不同地层损失率分析双线隧道的相互影响

在基于地层损失率的基础上分析双线隧道掘进开挖的相互影响，如图6所示，当土体损失为0.2%时，右线开挖对于左线中轴线上几乎无影响，并不会使得左线隧道中心线的地表沉降加大，只影响两隧道之间部分的地表土体。

图6 不同土体损失率下双线隧道地表沉降图

当土体损失为0.4%时，右线隧道开挖对于左线已开挖形成的沉降槽，具有明显的加大现象。

当土体损失达到0.6%时，右线隧道的开挖对于左线已形成的沉降槽的影响略微减小。

左线隧道中心地表沉降大于右线隧道中心地表沉降，其原因在于右线隧道上部存在桩基础，减小了隧道开挖对地表的影响，并且土体损失率越大，桩基础对于减小地表沉降的作用越明显。

3.3 地层损失率对站房变形影响

地表土体发生沉降和变形将会引起上部建筑物产生附加应力，附加应力将会导致上部建筑物发生变形、倾斜以及损坏等不良现象[16]。如图7所示的左线隧道中心上部地板竖向变形可知。

图7 不同损失率底板竖向变形

(1)随着土体损失率增大，底板竖向变形也成阶梯型增大。

(2)对于土体性质较差的土层，损失率的改变对其影响很大，当土体损失率达到0.4%时，站房底板的竖向沉降以达到4.66mm，为符合合肥市站房变形控制标准，需要控制地层损失率为0.4%左右。

3.4 掘进环数对地面沉降影响

如图8所示土体损失率为0.4%时的右线隧道中心沉降曲线可知在不同相隔环数情况下，地表沉降均是以相同沉降变形速率增大的，表明左右线以不同环数掘进，并不会影响地表沉降的最终值，当左右线相隔环数越大时，发生沉降变形所需计算步长越长，滞后性就越长，就可以有更多的时间观测地表变形是否超出规定便于及时加固。

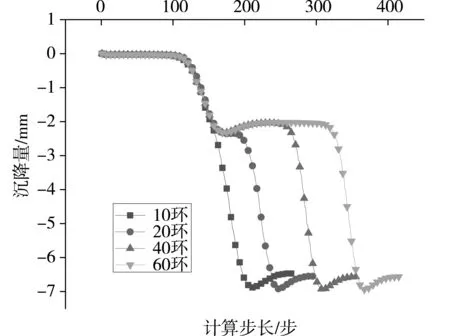
图8 不同间隔环数隧道中点沉降曲线

由横向沉降图9可知该沉降槽为“W”型，影响区域约为24m，是双线隧道盾构直径的两倍，其沉降槽最大处分别是左右线隧道中心出现。先工况1左线隧道开始开挖直至40环时，地表开始因左线开挖发生沉降，形成如图9(a)所示的单隧道沉降槽，其对应的地层沉降云如图9(b)所示。沉降达到最大3.57mm。然后工况2右线隧道开始开挖，形成如图9(c)所示一大一小的沉降槽，其对应的地层沉降云如图9(d)所示。由于右线的开挖不仅使得右线隧道影响区域地表发生下沉，还使得两隧道中心处发生一定沉降，但是右线的盾构掘进并不会对左线已开挖部分的沉降有太大的影响。直至右线隧道贯穿，如图9(e)所示，地表沉降形成了两个较为相等的沉降槽，，其对应的地层沉降云如图9(f)所示这里是因为左右线隧道中心相距较大，相互并不会发生较为明显的影响。

(a)右线未开挖横向沉降

3.5 掘进环数对站房结构变形影响

由于站房是现浇混凝土结构，自身弹性模量较大，在盾构开挖过程中，站房的中板和顶板未发现明显变形，只有底板随着地面沉降发生了较大形变，如图10所示，给出对于地层损失率为0.6%时，和左右线相隔环数为10环、20环、40环、60环时，两隧道之间上方站房底板的竖向变形曲线，可见：

图10 不同环数底板沉降竖向变形

(1)随着盾构掘进进程加深，站房底板沉降在随着施工计算步长在逐渐增大，最终趋于平稳，在左右线不同相隔环数情况下，底板最终变形都约为6.95mm；

(2)在左线隧道开挖时，不同相隔环数下底板变形均有先趋于平稳的阶段，相隔环数越大，平稳阶段的步长越长，这表明相隔环数越大，右线开挖对于底板变形的影响就越滞后；

(3)在右线开挖后，底边变形速率明显增大，这表明左右线的同时掘进将加大底板变形，不利于底板保持稳定，如果变形速率过快，变形量过大，可能会导致站房总体结构的不稳定。

4 结论

本文主要对合肥1号线盾构穿越合肥火车站进行分析，由于左右线掘进环数的不同，以及在不同地层损失率下对于地表沉降和站房底板变形的影响，得到的主要结论如下：

(1)因左右线隧道中心距较大，左右线相隔不同的掘进环数对于地表最终沉降影响不大，但对于其沉降速率影响较大，相隔环数越小，其沉降变形速率越大，对于控制沉降变形就越困难；

(2)左右线相隔环数越大，其沉降滞后性就越大，给予施工参数调整、二次补充注浆加固地层的时间就越长，由于该工程为重要施工节点和交通枢纽，其工期紧张，在保证地表沉降和站房变形安全的情况下，左右线最少需要相隔20环以上才能同时施工，并且在施工过程中应采取相应控制地表沉降的措施，如控制盾构施工参数等，尽可能的减小盾构开挖对土体的扰动；

(3)土体损失率对于地表沉降的影响较大，通过控制相关盾构掘进参数如，刀盘转速、扭矩、土仓压力以及同步注浆和二次补充注浆等措施控制土体损失率在0.4%以内将符合合肥市站房变形控制标准；

(4)当双线隧道的土层损失越大时，左右线相互影响越明显，对于合肥土层情况而言，控制土层损失率在0.2%以内，可使得后掘进隧道对于先掘进隧道几乎没有影响；

(5)当土体损失达到0.6%以上时，对于本项目而言，后开挖隧道对于先开挖隧道的影响相比于土体损失对于隧道的影响反而减小可得出，当土体损失较大时，在形成“W”型沉降槽情况下，双线隧道的影响反而在减小。如若土体损失足够大，双向隧道地表沉降将形成“V”型沉降槽，其先行开挖隧道和后行开挖隧道将不会对对方最大沉降造成影响，反而共同作用影响于两隧道中心位置。