基于精细温度观测的南海东北部陆坡-深海盆底层湍流混合*

李杨 , 黄鹏起 , 鲁远征 , 屈玲 , 郭双喜 ,4,5, 岑显荣 ,周生启,4,5, 张佳政, 丘学林,5

1. 热带海洋环境国家重点实验室(中国科学院南海海洋研究所), 广东 广州 510301;

2. 南方海洋科学与工程广东省实验室(广州), 广东 广州 511458;

3. 中国科学院边缘海与大洋地质重点实验室(中国科学院南海海洋研究所), 广东 广州 510301;

4. 中国科学院南海生态环境工程创新研究院, 广东 广州 510301;

5. 中国科学院大学, 北京 100049

海洋是地球系统的重要组成部分, 在维持全球能量收支平衡的过程中扮演着重要的角色(Simmons et al, 2011)。近年来, 人们不再局限于研究上层海洋,对深海也展开了探索。深海底层与沉积物、冷泉密切相关(Shanmugam, 2017; 赵斌 等, 2018), 是石油和天然气等自然资源的“冷藏库”。深海不仅贮藏着丰富的资源, 还蕴含着巨大的能量。Egbert 等(2000)估算出全球深海的斜压能量约为维持经向翻转环流能量(2TW)的一半。现场观测表明, 虽然底层海水温度变化只有10–3℃左右, 但深海同样存在活跃的湍流混合(Polzin et al, 1997; Ledwell et al, 2000; van Haren et al, 2011; Holtermann et al, 2012; Waterhouse et al, 2014; Zhao et al, 2016; Holmes et al, 2019)。深海湍流混合产生的上升流和下降流是驱动经向翻转环流的动力来源之一(Rahmstorf, 2003; Callies et al,2018), 也是海洋能量级串过程中至关重要的一环,影响着大尺度运动, 维持海洋层结。此外, 湍流混合将海水能量从海洋上层带到下层, 参与海洋热量、动量和能量的平衡过程(Munk et al, 1998); 同时控制温盐通量、营养盐、污染物和微生物的浓度分布,改善和保护海洋生态环境, 维持海洋生态系统的动态平衡(刘倩, 2016)。

20 世纪90 年代, Munk 等(1998)指出, 大洋平均混合率需达到10–4m2·s–1才能维持现今的大洋热盐环流强度。但开阔大洋的观测实验表明, 大部分海域的混合率仅为10–5m2·s–1。为此, 人们开始探寻强湍流混合海域。南海是存在强湍流混合的边缘海之一, 蕴含着丰富的海洋动力现象。吕宋海峡的双山脊地形与潮流相互作用产生大量内波(谢皆烁,2015), 为南海强湍流混合提供能量; 黑潮在吕宋海峡处入侵带来的中尺度涡对南海湍流混合也起着不可忽视的作用(李敏, 2013; Zhang et al, 2016)。大量观测实验表明, 海山(Toole et al, 1997)、海底山脊(Polzin et al, 1997)、大陆坡(Nash et al, 2007)和海底峡谷(Kunze et al, 2012)等海底地形复杂的海域均存在强湍流混合。南海海底地形复杂, 海山、海丘众多, 并有深海隆地和洼池。丰富的动力环境和地形条件, 使南海成为太平洋系统中不可替代的“混合加工厂”。西北太平洋的深层水、中层水和次表层水经吕宋海峡进入南海, 被充分混合后返回太平洋,一定程度上驱动大洋热盐环流(尚晓东 等, 2010)。由此可见, 开展南海湍流混合的研究具有重要的科学意义。

近年来, 不少科学家对南海北部湍流混合开展了一系列研究。在上中层海域, 基于南海北部-吕宋海峡-西北太平洋的断面微结构观测数据和参数化模式结果, Tian 等(2009)发现南海海域1000m以下的涡扩散系数为10–3m2·s–1, 比西北太平洋大2 个数量级。Shang 等(2017)测得吕宋海峡以西的南海上层海域的耗散率和跨密度涡扩散系数分别为8.3×10–9m2·s–3和2.7×10–5m2·s–1, 比南海中、南部高1 个数量级。在陆架、陆坡, 张效谦(2005)分析了南海陆架-陆坡区域的微结构湍流混合观测数据, 结果显示浅海陆架区域的湍动能耗散率和涡扩散系数较强, 均值可分别达到 5×10–7m2·s–3和 2×10–3m2·s–1,相当于大洋内区平均值的100 倍。Yang 等(2014)测得南海北部陆坡的湍动能耗散率为3.6×10–8m2·s–3,涡扩散系数为5.2×10–4m2·s–1。在深层海域, Yang 等(2016)通过Gregg-Henyey-Polzin 尺度方法计算出南海北部离海底 500m 处的涡扩散系数为10–4～10–3m2·s–1。Wang 等(2016)通过内潮模拟与能量学分析得到南海海底以上2000m 内的水柱湍动能耗散 率 为 10–8～10–6m2·s–3, 涡 扩 散 系 数 为 10–4～10–3m2·s–1。这些研究工作大都聚焦于南海中上层的湍流混合, 较少涉及底层。近年来, 深海观测技术的成熟为南海深海底层湍流混合的研究提供了许多观测资料。本文利用高分辨率温度传感器在海底上方0.5m 处持续观测4.4d 的温度数据, 分析南海东北部2216～3201m 深度范围内底层海水温度的时间变化特征, 根据Ellison 尺度方法计算底层的湍动能耗散率和涡扩散系数, 探讨地形粗糙度和内潮对底层湍流混合的影响。

1 数据和方法

1.1 现场观测数据

2019 年5 月14 日—20 日, 国家基金委南海地球 物 理 航 次 在 南 海 东 北 部 海 域(19°40′48″ —21°48′36″N, 118°43′12″—119°2′24″E)开展了底层海水温度观测。观测断面为陆坡-深海盆式断面(图1a 黑色实心圆), 东北-西南向横跨300km, 站位深度范围为2216～3201m, 各站位的海底地形粗糙度用20km×20km 内水深数据的方差表示(见表1), 水深数据是General Bathymatric Charts of the Oceans(GEBCO) 2014 地 形 数 据 (https://www.gebco.net/data_and_products/gebco_web_services/we b_map_service/gebco_2014_wms.html), 分辨率为30″。本次观测共投放25 台沉浮式OBS(ocean bottom seismometers)。固定在沉耦架上的OBS 被投放后,受沉耦架的重力作用而自由下落至海底并记录数据。待坐底记录完毕时, OBS 接收到声学释放指令,熔断钢丝熔断, OBS 与沉耦架脱离, 并利用自身的浮力漂浮至海面。温度传感器固定在OBS 的边缘,每台OBS 搭载1 或2 个温度传感器, 其中2、3、5、7、9、11、13、14、19、20、21 和22 号等11 个站位的OBS 上搭载2 个温度传感器, 分别以2-1、2-2等表示(详见表1)。除去工作错误和丢失的温度传感器, 测得有效温度数据的OBS 站位总计22 个(图1b黑色实心圆)。温度传感器测量OBS 下放、坐底和回收期间的海水温度信息, 坐底时温度传感器位于海底上方约0.5m 处。假设OBS 下放和回收时匀速运动, 根据站位水深和温度传感器入水、到底、离底、出水的时间, 可估算出OBS 的平均下降速度约为0.84m·s–1, 平均上升速度约为0.66m·s–1。温度传感器由广州欧纳电子科技有限公司开发生产, 传感器长12.8cm, 直径1.96cm, 重80g(含电池), 耐高压(～10000m 水深), 具备预先编程的采样模式, 方便每一次设置和操作, 噪音水平低(1.2×10–4℃), 分辨率为2×10–4℃, 精确度为±5×10–3℃。观测期间, 温度传感器的采样频率设为8Hz。因本航次未开展温盐深水文观测, 故选择国家基金委南海开放航次水文数据库中最靠近OBS 断面的CTD 数据(图1a 红色五角星)作为参考, 其观测时间为2017 年4 月30日, 其经、纬度分别为117°44′24″E、19°15′36″N。该观测内容由SBE-911plusCTD 直读式深海温盐深测量仪完成, 采样频率为 24Hz, 深度测量量程为0～6800m, 精度为量程的0.015%, 分辨率为量程的0.001%; 电导率测量精度为±3×10–4S·m–1, 分辨率为4×10–5S·m–1; 温度测量精度为±1×10–3℃, 分辨率为2×10–4℃。

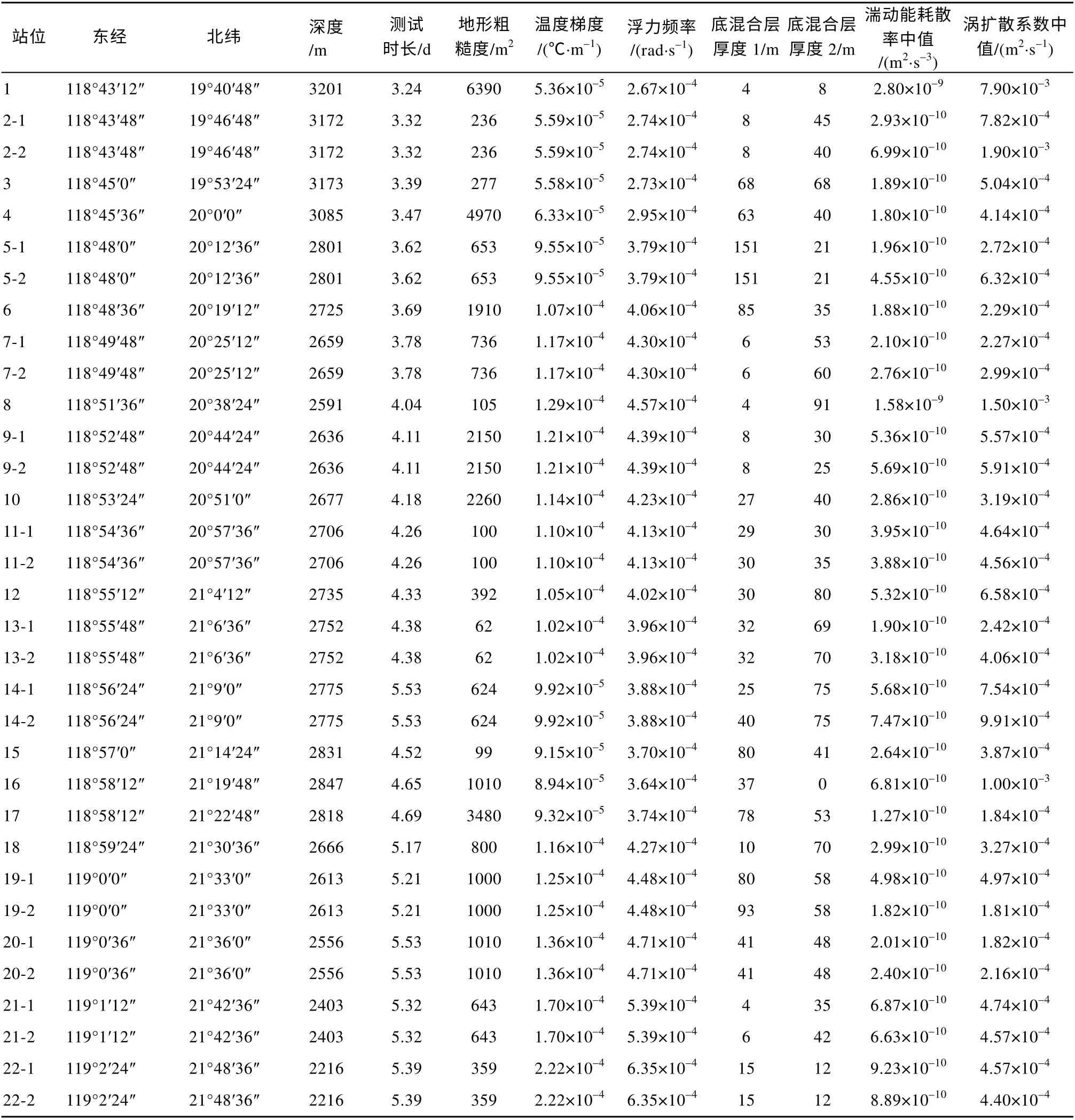
表1 各测站详细信息Tab. 1 Detailed information of each station

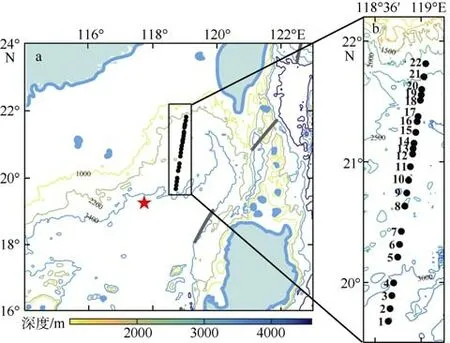
图1 研究区OBS 和CTD 站位示意图该图基于国家测绘地理信息局标准地图服务网站下载的审图号为GS(2016)1666 号的标准地图制作; 图中黑色实心圆为2019 年OBS 测站, 红色五角星为2017 年CTD 站位Fig. 1 (a) The location of the OBS and CTD stations; (b)Regional bathymetric map indicated by the solid rectangle in the left panel; black dots are the OBS stations in 2019,and red pentagram are the CTD station in 2017

1.2 数据处理方法

1.2.1 标定现场温度、位势温(密)度和浮力频率

温度传感器测得的原始数据为时间和电阻值。根据传感器校正参数, 将电阻值转化为温度后,根据OBS 下降、上升速度和温度传感器采集时间,推算出其深度信息, 得到OBS 下降和上升的温度廓线。由于测量数据为现场温度, 需将其转化为位势温度和位势密度, 再计算垂向温度梯度和浮力频率。以2017 年CTD 站位(图1a 红色五角星)测量的盐度作为参考盐度, 利用Gibbs-Sea Water 工具包, 将现场温度廓线转化为位势温度廓线和位势密度廓线。图2a、b 和c 中的灰线分别表示所有温度传感器的现场温度、位势温度和位势密度廓线。

根据所有温度传感器下放和回收测量所获得的廓线, 统计计算得到该海域不同深度的平均层结和温度梯度, 作为各个站位的背景层结和温度梯度。其计算步骤如下:

1) 由位势温度廓线计算温度梯度dθ/dz廓线(图2d 灰线所示);

3) 求出每个站位2200～3200m 深度范围内每个深度对应的温度梯度和浮力频率中值, 线性拟合温度梯度、浮力频率与深度的关系式(拟合直线由图2d 和图2e 中的黑线表示); 根据各站位水深, 得到背景温度梯度和浮力频率(如图2d 和图2e 黑线上的点所示)。

各站位背景温度梯度和浮力频率具体数值详见表1。图2 中温度传感器观测廓线(灰)及温度梯度/浮力频率拟合直线(黑)和CTD 对应的观测廓线(红)吻合较好。

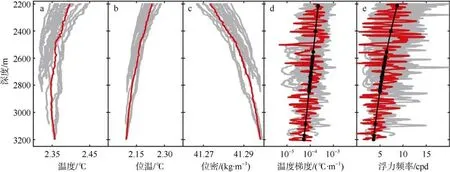
图2 温度传感器(灰)和CTD 数据廓线(红)对比图a. 现场温度; b. 位势温度; c. 位势密度; d. 温度梯度; e. 浮力频率; 图d 和e 中的黑色线为拟合直线, 黑点代表背景值Fig. 2 Comparison of vertical profiles obtained with the temperature loggers (gray) and historical CTD data (red): (a)in-situ temperature; (b) potential temperature; (c) potential density; (d) temperature gradient; (e) buoyancy frequency. The black dotted line in (d) and (e) is the fitting line

1.2.2 湍动能耗散率和涡扩散系数

2 结果

2.1 底混合层

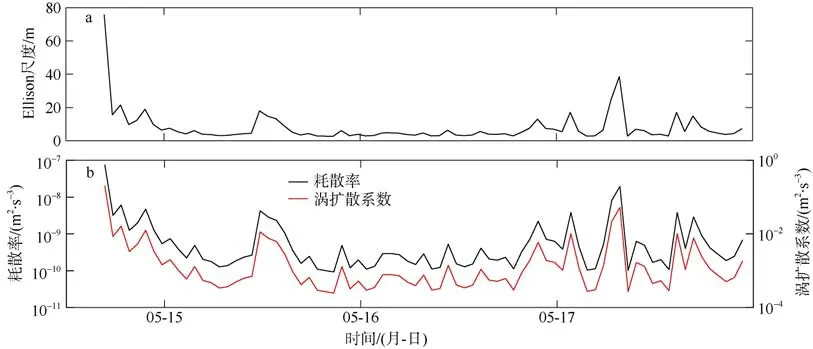
图3 2 号站位Ellison 尺度(a)、湍动能耗散率和涡扩散系数时间序列(b)Fig. 3 Time series of turbulent kinetic energy dissipation rate and turbulent diffusion at station 2: (a) Ellison scale; (b)dissipation rate (black) and turbulent diffusivity (red)

海洋底层是海洋水体和地球固体边界发生相互作用的交界处, 是海水能量的重要耗散地。海流和内波等动力过程经过海底粗糙地形, 发生剪切作用,造成水体翻转混合, 从而形成海底混合层(Turnewitsch et al, 2003)。首先, 本文关注各站位近海底是否存在混合层结构, 以及底混合层的特征变化。基于OBS 下放和回收时温度传感器测得的温度廓线, 根据混合层内海水温度均匀这一特征判断底混合层BML(bottom mixed layer)的存在情况。从海底向上看, 当某一深度海水与底层海水的温度差超过阈值0.005℃时, 定义该深度到海底的距离为底混合层厚度(Beaulieu et al, 1998; Lozovatsky et al,2012)。图4 展示了各站位OBS 下放和回收时温度传感器测得的温度廓线。在13～19 号站位, 混合层厚度最大可达近100m, 而在16 号站位的上升廓线未发现底混合层。整个观测断面底混合层厚度变化范围是0～151m(表1), 中值是37m。对于一般的下放式CTD, 回收时水体受到大体积采水瓶扰动, 传感器测量的数据存在很大误差, 因此分析时选用下放廓线, 而不选用回收廓线。由于本次观测温度传感器放置于OBS 旁侧, 扰动误差较小, 其下放和回收廓线可对比使用。如表1 和图4 所示, 在大部分站位的下降和上升温度廓线中, 发现底混合层厚度并不相同。在观测的4.4d 内, 下降廓线与上升廓线的底混合层厚度平均变化24m。在4～6 号站位, 下降廓线的底混合层比上升廓线厚, 例如5 号站位的底混合层厚度变化最大, OBS 下降和上升前后的底混合层厚度分别为151m 和21m, 厚度变化为130m。这说明深海存在复杂多变的动力过程, 使得底混合层厚度在短短的4.4d 内就发生了改变。

图4 各站位OBS 下放(黑线)和回收(红线)过程的位势温度廓线a. 1～12 号站位; b. 13～22 号站位Fig. 4 Potential temperature profiles acquired in the deployment (black) and recovery (red) processes at each site:(a) stations 1～12; (b) stations 13～22

2.2 底层温度的分布特征

深海底层温度是反映深海底边界层动力过程和结构的基础参量。本文通过各站位的底层海水温度时间序列分析海水温度的变化特征。图5a 展示了各站位底层海水温度时间序列中值随纬度的变化, 其中1～16 号站位位于深海盆, 17～22 号站位位于陆坡-深海盆过渡区, 整个观测断面的底层海水温度时间序列中值为2.08～2.21℃。对比图5c 发现, 底层海水温度中值随纬度的变化趋势与地形变化趋势基本相同。本次观测测得南海东北部2216～3201m 深度范围内, 深海盆及陆坡-深海盆过渡区海底上方0.5m 处, 底层海水温度在2.15℃上下波动。

图5 各站位底层温度和湍流混合的空间分布a. 位温中值和浮力频率, 其中误差棒代表温度的标准差; b. 湍动能耗散率和涡扩散系数; c. 地形起伏Fig. 5 Spatial distribution of turbulent mixing and bottom temperature at each station: (a) median value of potential temperature and buoyancy frequency, the error bar represents the standard deviation of temperature; (b) turbulent kinetic energy dissipation rate and turbulent diffusivity; (c) topographic relief

各站位底层海水温度的时间序列如图6 所示,图中各站位按深度由浅到深依次排列。为能更直观地展示各站位底层海水的温度变化, 将各站位底层海水温度的时间序列向上或向下平移。由于科考船从1 号站位依次向北下放和回收OBS, 各站位的底层海水温度时间序列起始时间并不相同。由图6 可知, 各站位底层海水温度随着站位深度的增加而减小, 但各站位底层海水温度的低频波动并非随着深度的增加而单调地减小。图6 中各站位底层海水的温度波动大小随深度的变化未呈现出明显的规律,如15、17 和19 号站位底层海水温度波动较小, 而1、9、14 和16 号站位波动较大。深度最深(3201m)的1号站位, 其温度波动可达0.2℃。此外, 11、14 和22号站位底层海水温度在保持涨落的同时整体呈上升趋势, 而5 号站位呈下降趋势。由此可见, 深海底层海水并非都处于稳定状态。

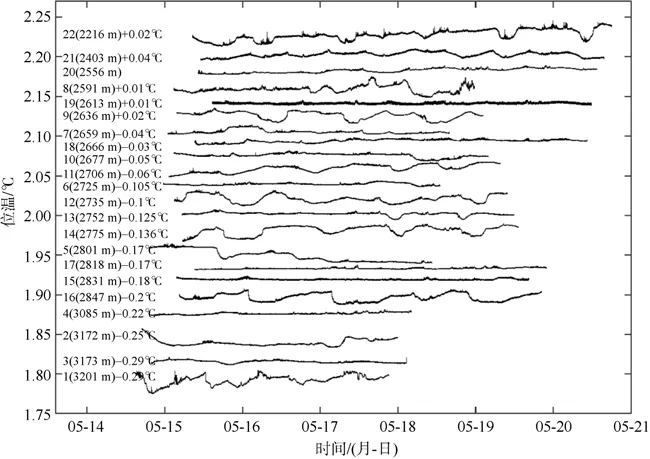
图6 各站位底层海水温度时间序列图中左侧文字标注为: 站位号(站位水深)+/-平移温度值Fig. 6 Time series of bottom-water temperature at each station

海水的温度高频涨落间接反映水体的不稳定性,是利用Ellison 尺度方法估算湍流耗散率的数据基础。图7a 表示各站位底层海水温度时间序列的标准差随站位深度的分布, 计算标准差时去除了低频的温度波动, 具体计算方法见本文1.2.2 节。本次观测断面底层海水的温度变化量级约为10–4～10–3℃。与温度波动相同, 温度涨落与站位深度也不存在明显的正比关系。1 号站位比3 号站位深28m, 该站位底层海水温度的涨落却是3 号站位的近4 倍。16 和17号站位相邻, 深度仅相差29m, 16 号站位底层海水的温度涨落却是17 号站位的近6 倍。综上可知, 底层海水温度低频的波动和高频的涨落均未随深度的增加而减小, 表明各观测站位的动力环境并不相同,深水站位可能存在较强的动力过程。

图7 各站位底层温度和湍流混合随站位深度的分布a. 温度时间序列标准差; b. 湍动能耗散率; c. 涡扩散系数Fig. 7 Distributions of bottom temperature and turbulent mixing with depth: (a) standard deviation of temperature time series;(b) turbulent kinetic energy dissipation rate; (c) turbulent diffusivity

2.3 湍流混合的分布特征

本文基于Ellison 尺度方法估算了各站位的湍流混合大小(表1)。图5b 给出了各站位底层湍动能耗散率(黑)和涡扩散系数(红)时间序列中值随纬度的分布。纬度最低处1 号站位湍流混合最强, 湍动能耗 散 率 为 2.8×10–9m2·s–3, 涡 扩 散 系 数 为7.9×10–3m2·s–1。随着纬度的增高, 2～7 号站位的湍流混合呈减小趋势, 湍动能耗散率在7 号站位减小至2.1×10–10m2·s–3, 涡扩散系数减小至2.27×10–4m2·s–1。随后湍动能耗散率在 8 号站位增大至1.58×10–9m2·s–3, 涡扩散系数减小至 1.5×10–3m2·s–1,仅次于1 号站位。9～22 号站位的湍动能耗散率在4.42×10–10m2·s–3上 下 波 动, 涡 扩 散 系 数 在4.66×10–4m2·s–1上下波动。对比图5c 发现, 湍动能耗散率和涡扩散系数随纬度的变化趋势与地形变化趋势有一定的相似性。

为进一步分析两者与地形深度的关系, 由图7b和图7c 分别给出各站位的中值及平均值随站位深度的变化。由图7b 和图7c 可知, 无论是中值还是平均值, 不同站位深度的耗散率大小相当, 略有减小。中值变化范围为1.3×10–10～2.8×10–9m2·s–3, 平均值变化范围为4.6×10–10～1.1×10–8m2·s–3。由于该海域底层海水层结相差较小(见图2e ), 不同站位深度的涡扩散系数同样大小相当, 中值和平均值变化范围分别是1.8×10–4～7.9×10–3m2·s–1和6.7×10–4～3.1×10–2m2·s–1。1 号站位深度最深, 但其耗散率与涡扩散系数却是最大, 平均值甚至可达 1.1×10–8m2·s–3和3.1×10–2m2·s–1。对比深度相近的1 和3 号站位及16和17 号站位, 1 号站位的湍动能耗散率和涡扩散系数比3 号站位大1 个数量级, 16 号站位的湍动能耗散率和涡扩散系数是17 号站位的4 倍。综上所述,由于观测位置距海底约0.5m, 处于海水与固地边界作用的底边界层内, 其海底的混合无论深度大或小,耗散率与扩散系数均较大。底层不同站位之间也存在明显的空间差异, 其变化约在1 个量级范围内。深海盆(1～16 号站位)及陆坡-深海盆过渡区(17～22号站位)底层的湍动能耗散率量级为10–10～10–9m2·s–3,涡扩散系数量级为10–4～10–3m2·s–1, 比开阔大洋背景扩散系数(10–5m2·s–1)高出1～2 个数量级。

3 讨论

3.1 地形粗糙度对底层湍流混合的影响

由图6 和图7 可知, 南海北部近海底存在较强的湍流混合, 同时呈现出明显的空间差异性, 这可能是由局地地形的不同粗糙程度引起。大量观测实验表明, 海山、海底山脊、大陆坡和海底峡谷等海底地形粗糙度大的海域均存在强湍流混合(Toole et al, 1997; Polzin et al, 1997; Nash et al, 2007; Kunze et al, 2012)。为探究海底地形粗糙度对底层湍流混合的影响, 由图8 给出各站位湍动能耗散率(黑)和涡扩散系数(红)随地形粗糙度的变化分布, 图中数字标号为站位号。结合图5c 的地形可知, 1 号站位地形粗糙度最大, 位于海山山顶, 底层湍流混合最强。17号站位位于陆坡-深海盆过渡区的凹槽, 地形粗糙度也较大, 但底层湍流混合却最小。16 号站位与17号站位相邻, 其地形粗糙度为17 号站位的1/3, 但湍动能耗散率和涡扩散系数却是17 号站位的4～5倍。8 号站位地形粗糙度较小, 位于海山山脚, 但湍流混合较强, 仅次于1 号站位。另外, 从图8 可以看出, 无论是耗散率还是涡扩散系数, 两者均未随地形粗糙度的增加而增大。除去1 号站位, 耗散率和涡扩散系数随地形粗糙度的增加甚至有减小的趋势。这说明现有观测数据未能显示底层湍流混合与地形粗糙度存在明显的相关性。过去不少研究工作发现, 底层混合随地形粗糙度的增大而增大。例如,Jing 等(2011)发现西北太平洋盆地中部海槽和Okidaito 海脊处海底地形粗糙度为3×105m2, 该处近海底1500m 的扩散系数达10–4m2·s–1, 比平坦地形处高出1 个数量级。本文观测点非常靠近海底(离底0.5m), 局地的底层动力环境和地形对观测点的湍流混合影响更大, 而观测断面不同站位的局地底层环境和地形可能存在较大差异, 造成底层湍流混合与地形粗糙度的相关性不明显。Huang 等(2021)基于2018 年在南海北部测量的底层海水温度数据, 同样没有发现湍流混合与地形粗糙度存在明显的相关性。此外, 本文各站位的地形粗糙度均较小且变化范围小(102～103m2), 可能未体现出地形粗糙度的影响。根据Li 等(2014)对西北太平洋底层混合和地形粗糙度关系的研究, 地形粗糙度变化范围达到4 个量级(102～106m2)才能显示出两者的相关规律。

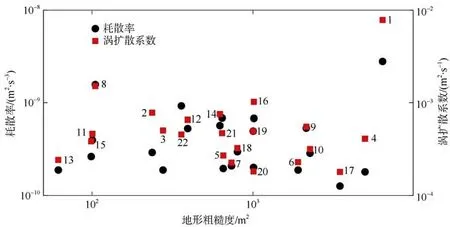
图8 不同地形粗糙度下各站位的湍动能耗散率和涡扩散系数图中同一站位的耗散率和涡扩散系数呈垂直对应Fig. 8 Turbulent kinetic energy dissipation rate (black) and turbulent diffusivity (red) at each station with different terrain roughness

3.2 内潮对底层湍流混合的影响

相对海表而言, 由风产生的机械能输入对深海底层的影响较小, 内潮是深海混合过程的主要能量来源。赵玖强(2019)通过利用南海深海锚系观测系统发现南海北部深海以全日潮占主导地位。本文推测各站位底层湍流混合的差异可能与内潮有关。

将22 个站位底层海水温度时间序列减去平均温度, 计算功率谱, 得到温度信号在不同频率上的能量分布。结果表明每个站位的能谱峰值位置所对应的频率并不相同(图9), 大致可划分为4 种类型:1、2、3、6、9、16 号站位存在明显的全日信号(图9a); 19、21、22 号站位存在明显的半日信号(图9d);8、9、11、12、13、14、15、20 号站位既有明显的全日信号又存在明显的半日信号(图9b); 而4、5、7、10、17、18 号站位的全日与半日信号均不明显(图9c)。结合各站位的地形分布 (图5c)发现, 具有全日信号的站位多数位于深度较深的海盆区域; 而半日信号较强的站位主要位于断面北部较浅的陆坡-海盆过渡区(19～22 号站位); 在两者中间的过渡区域,既存在全日与半日信号较强的站位, 也存在无全日与半日信号的站位。

图9 2019 年5 月观测期间1、4、8 和19 号站位的温度功率谱图中虚线分别表示全日和半日潮频率Fig. 9 Temperature variance spectra at stations 1, 4, 8, and 19 over the entire observational period in May 2019. Dashed lines denote durnal and semi-durnal tide frequencies

图5b 中除1 号站位外, 以20°30'N 为分界线,20°30'N 以北的站位(8～22 号站位)湍动能耗散率中值为4.98×10–10m2·s–3, 20°30'N 以南的站位(2～7 号站位)湍动能耗散率中值为1.92×10–10m2·s–3, 北侧站位的湍动能耗散率明显强于南侧站位。观测断面全日、半日内潮的空间分布及底层湍流混合的南北差异与Xu 等(2014)提出的吕宋海峡以西深海盆内内潮生成的南北不对称性是一致的。正压潮流经吕宋海峡时, 与海峡内地形发生相互作用,激发产生内潮。吕宋海峡地形在经向上呈不对称,内潮由于在反射和折射过程中受到不同地形的影响, 在纬向和经向上都呈现出高度的空间差异性。内潮向西传播导致了吕宋海峡以西深海盆内内潮的南北不对称性, 具体表现为深海盆南侧(19°30'N)的全日内潮动能是半日内潮的 3～4 倍,而北侧(21°N)的全日内潮能量与半日内潮相当。此外, 内潮在传播过程中, 受背景场的影响表现出非相干性。内潮在吕宋海峡生成后, 向北传播的距离大于向南传播的距离, 北侧的非相干信号强于南侧(Xu et al, 2013, 2014; Cao et al, 2017),这也和本文北侧底层湍流混合强于南侧的情况一致。

基于由温度功率谱划分的4 种不同类型的站位, 本文分别选取了1、4、8 和19 号站位, 分析其温度和耗散率的时间变化特征。图10 展示了这4 个站位在5 月15 日—20 日期间的底层海水温度、底层湍动能耗散率和正压潮潮高时间序列, 正压潮潮高由TPXO8.0 潮汐工具包计算得到。如图10所示, 4 个站位的正压潮变化基本一致, 但不同站位的底层温度与耗散率变化却差异很大, 因此推测底层温度变化受正压潮的影响较小。这些站位的温度变化包含不同周期(数小时至一天)的涨落,说明温度变化受斜压潮(内潮)影响更大。再者, 大多数站位的温度能谱在全日和半日频带区间出现谱峰, 表明全日、半日内潮在底层海水温度变化中起主要调制作用。大量观测研究发现南海北部存在异常活跃的内潮活动(Zhao et al, 2004; Simmon et al, 2011; Ma et al, 2013; 梁辉等, 2016), 本文的观测结果也印证了这一点。

图10 2019 年1(黑)、4(蓝)、8(红)和19(灰)号站位底层位温(a)、湍动能耗散率(b)和正压潮潮高时间序列(c)Fig. 10 Time series of bottom temperature at stations 1 (black), 4 (blue), 8 (red), and 19 (gray) in 2019: (a) bottom potential temperature; (b) turbulent kinetic energy dissipation rate; (c) barotropic tidal elevation predicted from TPXO 8.0

4 结论

本文基于高分辨率温度传感器于2019 年5 月在南海东北部22 个站位海底上方0.5m 处持续观测4.4d 的温度数据, 分析了2216～3201m 范围内底层海水温度的时间变化特征, 根据Ellison 尺度方法计算了底层湍动能耗散率和涡扩散系数, 探讨了地形粗糙度和内潮对底层湍流混合的影响。

底混合层厚度无论是在空间还是时间上都存在巨大的差异, 4.4d 内同一站位的混合层厚度最大可相差130m。观测断面的底层海水温度为2.08～2.21℃,各站位底层海水的温度变化量级约为10–4～10–3℃,温度的低频波动及高频涨落都并非随着深度的增加而减小, 表明南海东北部底层存在丰富的具有时空差异性的动力过程。

由Ellison 尺度方法估算的混合参数表明, 深海盆及陆坡-深海盆过渡区的底层湍动能耗散率量级为10–10～10–9m2·s–3, 涡扩散系数量级为10–4～10–3m2·s–1, 整体比开阔大洋高1～2 个量级。底层混合同样存在明显的空间差异特征, 耗散率与涡扩散系数随深度的增加没有出现显著的减小趋势。湍动能耗散率和涡扩散系数均未随地形粗糙度的增加而增大, 现有观测数据未能显现底层湍流混合与地形粗糙度存在明显的相关性。通过分析各站位的温度能谱图发现存在4 种不同的谱型,全日和半日信号情况各异。对比4 种类型站位的温度、耗散率与正压潮潮高的时间变化, 发现温度变化更多地受斜压潮影响, 全日、半日内潮起主要调制作用。底层湍流混合的空间分布特征与吕宋海峡以西深海盆内潮的南北不对称性相似。与以往的南海湍流混合研究结果相比, 本方法计算得到的混合大小在合理范围之内。对于内潮的南北不对称性影响底层湍流混合空间差异性的具体机制, 有待结合高分辨率模式及精细地形开展进一步的研究。