地基GNSS接收伪距信号中的日重复项

张帝鑫，陈界宏，苏小宁，孙杨轶，林 恺，徐 锐，孟国杰，叶大纲

地基GNSS接收伪距信号中的日重复项

张帝鑫1，陈界宏1，苏小宁2，孙杨轶1，林 恺1，徐 锐3，孟国杰4，叶大纲5

（1. 中国地质大学（武汉） 地球物理与空间信息学院，湖北 武汉 430074；2. 兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070；3. 四川省地震局，四川 成都 610041；4. 中国地震局地震预测研究所 地震预测重点实验室，北京 100036；5. 台北大学 不动产与城乡环境学系，台湾 新北 23741）

多路径误差每天重复出现，是存在于伪距信号中的日重复项。伪距中的多路径误差可通过滤波的方法提取，但在多路径误差信号和噪声信号频率未知或者重叠的情况下，不能将二者完全分开。本研究尝试提出一种新技术解决这个问题，将伪距中卫星与台站的距离、钟差、硬件延迟、电离层延迟、对流层干延迟项消除后，得到包含多路径误差、对流层湿延迟和观测噪声的残差数据，再通过主成分分析的方法提取多路径误差。通过主成分分析法得到重构的第一主成分每天都重复出现，其亦为伪距信号中的日重复项，理论上是多路径误差。然而，日重复项的数值大小是前人研究的4到5倍。这表明伪距信号中还包含了除多路径误差以外的其他日重复项。通过分析17个台站的结果，本研究发现上述的其他日重复项，在使用相同类型接收机主机的台站之间的相关性更高。这反映了该日重复项与接收机主机型号有关，可能是与接收机主机相关的系统误差。

多路径误差；日重复项；主成分分析法；接收机主机误差

0 引言

全球卫星导航系统（global navigation satellite system, GNSS）卫星信号在向地表发射并传播到地面接收机的过程中，会受到卫星钟差、卫星硬件延迟、电离层延迟、对流层延迟、地面多路径误差、接收机钟差、接收机硬件延迟等影响[1]。这些因素均会影响定位精度，需要采取一定的方法和措施加以消除或削弱。钟差和硬件延迟能通过差分技术消除[2]。电离层延迟和对流层延迟通过建立模型消除[3-4]。然而，多路径误差不仅不能通过差分技术消除，而且无法建立适用于每个台站的改正模型。

多路径误差是由被台站附近的建筑物、植被或者地面等所反射的卫星信号进入接收机天线，对直达卫星的信号产生干扰而产生。由于卫星轨道和台站周围环境基本不变，多路径误差每天重复出现，其是存在于信号中的日重复项。多路径误差严重时会引起信号的失锁，是GNSS观测中的一个重要的误差源[1]。事后数据处理是削弱多路径误差主要采取的方法。多路径误差根据研究对象可分为三类，分别是载波相位、伪距和定位结果。载波相位上的多路径误差可通过建立单个台站的数学模型减弱[5]，或者通过分析信号的信噪比进行削弱[6-7]。伪距中多路径误差，可通过伪距和载波相位的线性组合进行评估[8]。但是，由于评估值中还包含了观测噪声，还需进一步处理，如通过有限脉冲响应（finite impulse response, FIR）滤波[9]或者自适应滤波[10]。在利用载波相位和伪距信号定位之前，未削弱原始信号中多路径误差，导致定位结果中受多路径误差的影响。对此，文献[11]提出小波滤波法，文献[12]采用自适应小波变换方法。

伪距上的多路径误差需要通过伪距和载波相位的线性组合评估后，再通过滤波提取。在观测噪声的频率和多路径误差的频率未知或者重叠的情况下，滤波的方法不能将二者完全分离。为了解决这个问题，本研究根据多路径误差每天重复出现的特征，尝试提出一种新方法。在将伪距中的卫星与台站距离、钟差、硬件延迟、电离层延迟、对流层干延迟项消除后，得到包含多路径误差、对流层湿延迟、观测噪声的残差数据，再根据多路径误差重复出现的特征，通过主成分分析法提取多路径误差。

1 原始数据

本研究使用了17个位于中国香港卫星定位参考站网的地基GNSS台站的观测数据。17个台站的位置如图1所示。

图1 台站分布图（倒三角形、正三角形、圆形，正方形均表示台站位置）

根据台站观测文件提供的信息可知，4个台站使用TRIMBLE NETR9型号的天宝接收机主机（简称天宝主机）和TRM59800.00 SCIS/SCIT型号的天宝接收天线（简称天宝天线），11个台站使用LEICA GR50型号的徕卡接收机主机（简称徕卡主机）和LEIAR25.R4 LEIT型号的徕卡接收天线（简称徕卡天线），另外T430台站使用LEICA GR50型号的徕卡主机和TRM59800.00 SCIT型号的天宝天线，HKKS台站使用TRIMBLE NETR9型号的天宝主机和TRM59800.00 SCIT型号的天宝天线，在3月30号接收主机更换为LEICA GR50型号的徕卡主机。本研究使用2018年德国地球科学研究中心的快速精密星历文件，用于计算卫星与台站之间的几何距离。

2 多路径误差的提取

GNSS卫星信号在传播过程中会受到诸多因素影响。其伪距的观测方程[1]表达式为

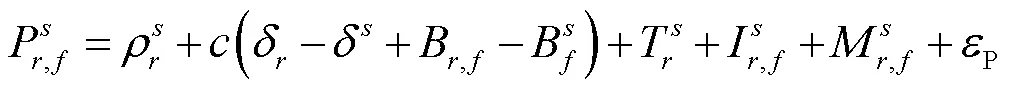
本研究从原始的伪距观测数据中，扣除星站距离、电离层延迟和对流层静力延迟，并通过去线性趋势减去钟差、硬件延迟，得到包含多路径误差、对流层湿延迟、观测噪声的残差数据，即研究数据。此处以HKOH台站接收北斗卫星导航系统（BeiDou navigation satellite system, BDS）C03同步卫星的B1频段信号为例展示。图2（a）为原始伪距观测数据。在多种摄动因素的影响下，同步卫星会产生周期性振荡，在赤道面上下来回运动[21]。因此在一天的时间尺度内，伪距数据呈余弦变化规律。图2（b）为星站距离，其数值与伪距接近，变化趋势与伪距一致。图2（c）为B1频段的电离层延迟量，其是通过双频载波相位计算，是相对值。图2（d）为对流层静力延迟，其数值在2.5～2.6 m之间，一天内变化幅度较小。图2（e）为伪距扣除星站距离、电离层延迟、对流层静力延迟、钟差和硬件延迟后，得到的包含多路径误差、对流层湿延迟、观测噪声的残差数据。

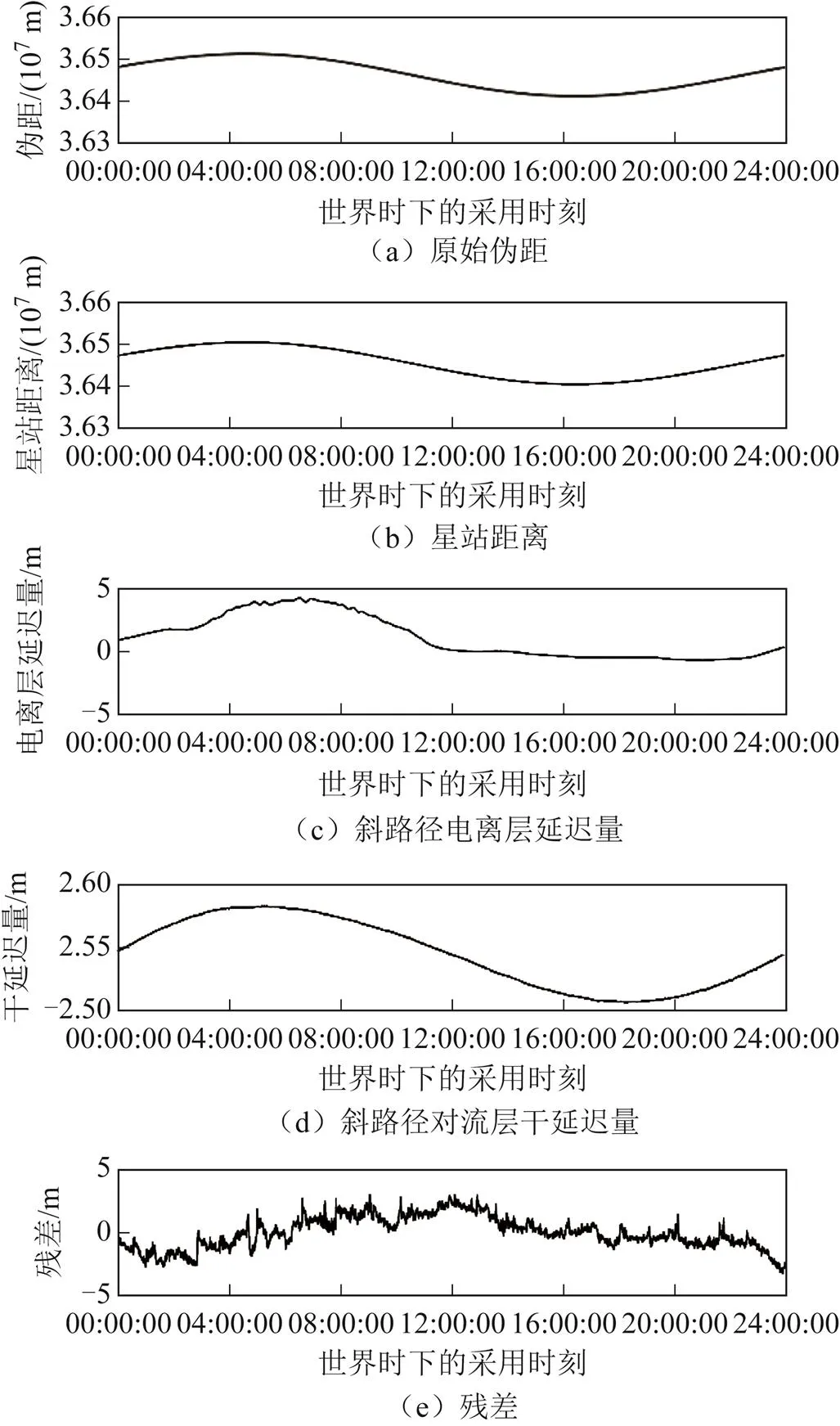
图2 HKOH台站与BDS C03同步卫星之间的物理量

本研究中，台站的观测数据和气象数据，以及快速精密星历文件均被使用。任何一种数据缺失或者不完整，均无法求得研究数据。以2018年1月为例，31 d中有4 d数据不完整，如图3所示。

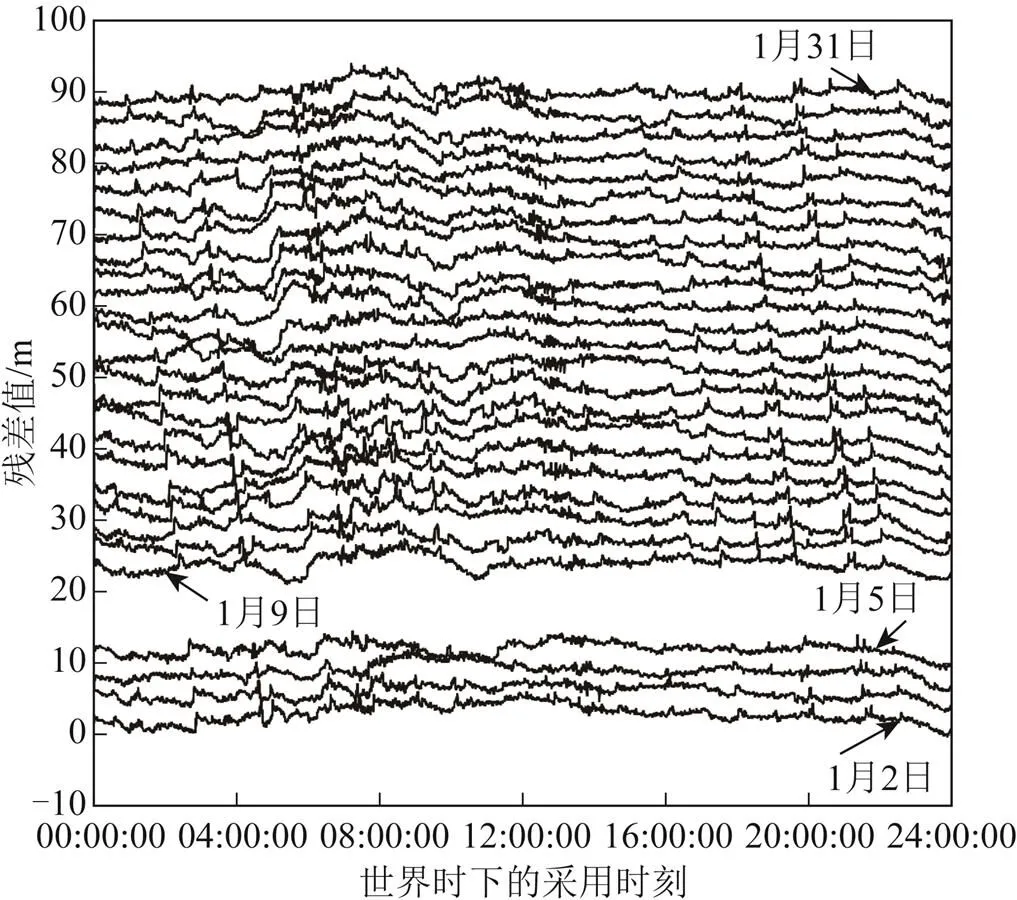
图3 2018年1月的残差数据

在图3中，每天数据都进行了等间距（3 m）纵向平移。部分波动特征每天都存在，并且随着日期增加会偏移。这些重复出现的波动特征可能是由多路径误差产生的。研究表明，BDS C03同步卫星轨道振荡周期与地球自转周期一致，约为23 h 56 min 4 s[22]。与卫星轨道位置紧密相关的多路径误差周期与地球自转周期一致[23]。与前一天相比，每天的多路径误差提前4 min左右出现。为了提取多路径误差，需要将每天的数据中相同的波动特征移动至相同时刻。考虑到GNSS台站的采样间隔为30 s，以起始第一天的时间为基准，将之后第天的时间依次增加（-1）×4 min，而后截取所有天数共有的时间段内的数据用于提取多路径。图4是图3的数据经过移动后并截取的结果，数据长度为2672个历元。

多路径误差每天都会重复出现，而对流层湿延迟和观测噪声具有随机性。以连续若干天包含多路径误差、对流层湿延迟、观测噪声的残差数据作为若干个原始指标，通过主成分分析法，可提取每天重复出现的部分，即多路径误差。主成分分析法是利用降维的思想，在损失最少信息的前提下把多个指标转为几个综合指标的多元统计方法。其本质是利用原始变量的线性组合形成几个综合指标（主成分），在保存原始变量主要信息的前提下起到降维与简化的作用。每一个主成分都是各原始变量的线性组合，并且每个主成分之间互不相关。在信号处理上，主成分分析法用于原始数据降噪。

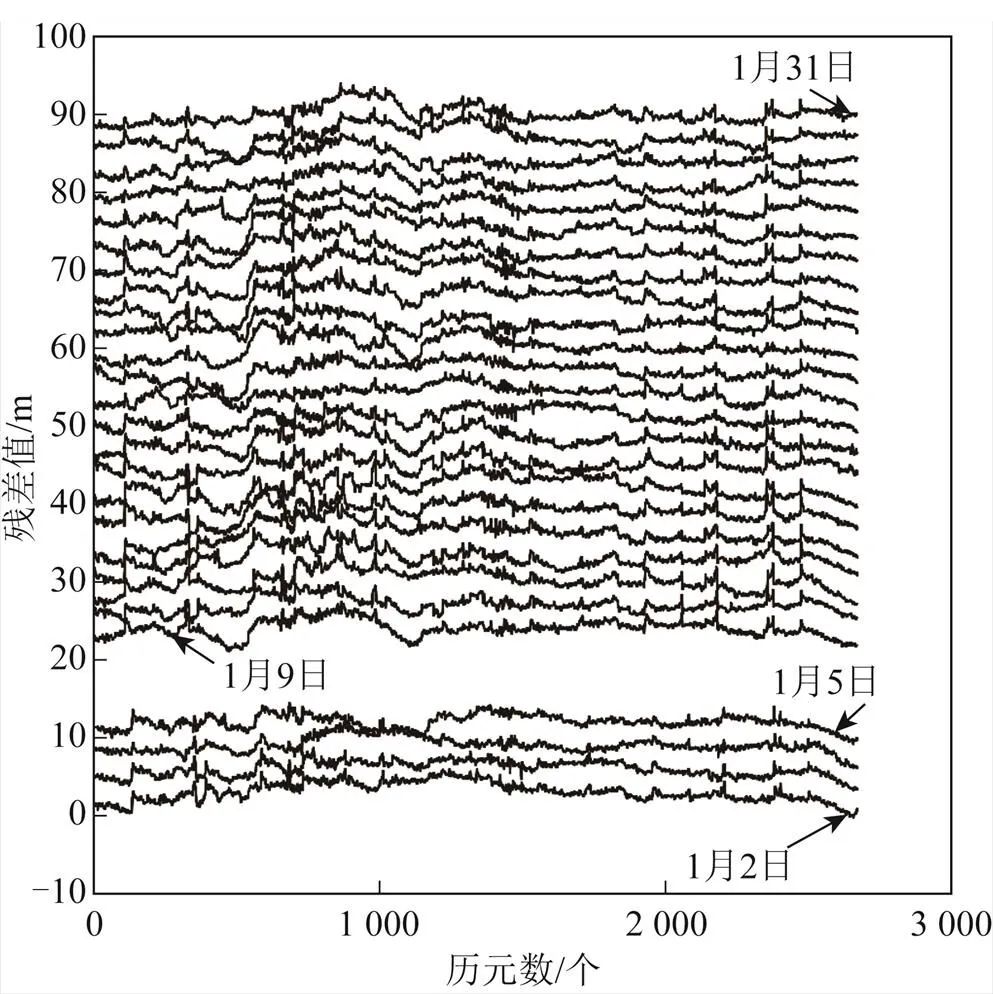
图4 2018年1月经时间移动并截取的残差的数据

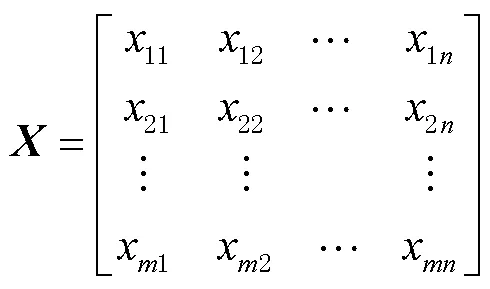
则矩阵的协方差矩阵为

可求得协方差矩阵的特征方程为

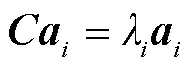
第主成分的贡献率表示为

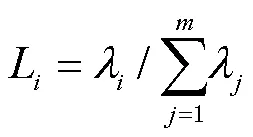
根据累计贡献率选择前个主成分，将原来的个变量转变为个变量。在数据处理过程中，需

对前个主成分进行重构，得到一个近似的矩阵为

3 试验结果

对HKOH台站27 d的数据做主成分分析，其各个主成分的贡献率如表1所示。

表1 主成分的贡献率

从表1可以看出：第一至第五主成分的贡献率分别为68.71 %、7.63 %、4.81 %、3.96 %和2.23 %；第6至第20主成分的贡献率从2.17 %减小至0.15 %。判断哪些主成分包含多路径误差的成分，需要根据重构后的各个主成分所体现特征辨别。图5（a）和图5（b）分别是通过纵向等间距（2 m）移动后的重构的第一主成分和第二主成分。

图5中重构的第一主成分基本一致且重复出现，而重构的第二主成分在27 d里存在明显差异。根据贡献度大小可知，重构的其他主成分每天的差异更大，此处不做展示。因此，通过主成分分析法，从包含多路径误差、对流层湿延迟、观测噪声的残差数据中提取的第一主成分，是伪距信号中的日重复项，每天重复出现，理论上为多路径误差。

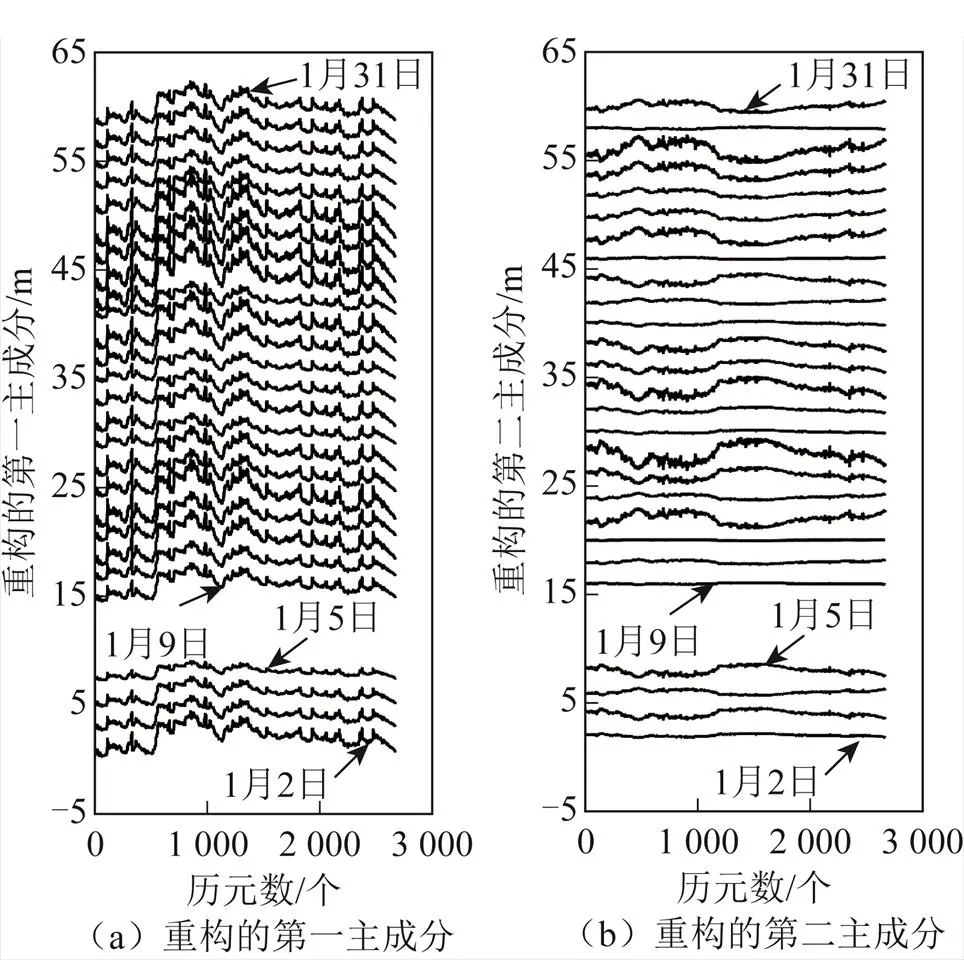
图5 一月份重构的主成分

本研究对2018年2月的数据进行与2018年1月数据相同的处理，得到2018年2月的第一主成分贡献率为70.11 %，并且将第一主成分进行重构。图6为1月和2月重构的第一主成分，图6中每天的数据都经过纵向等间距（2 m）移动，其中2月份只有为20 d。随着天数的增加，日重复项（重构的第一主成分）的波动特征每天较前一天提前出现，并且从1月持续到2月。若重构的第一主成分是真实多路径误差，这表明利用本研究的方法提取多路径误差是可行的。

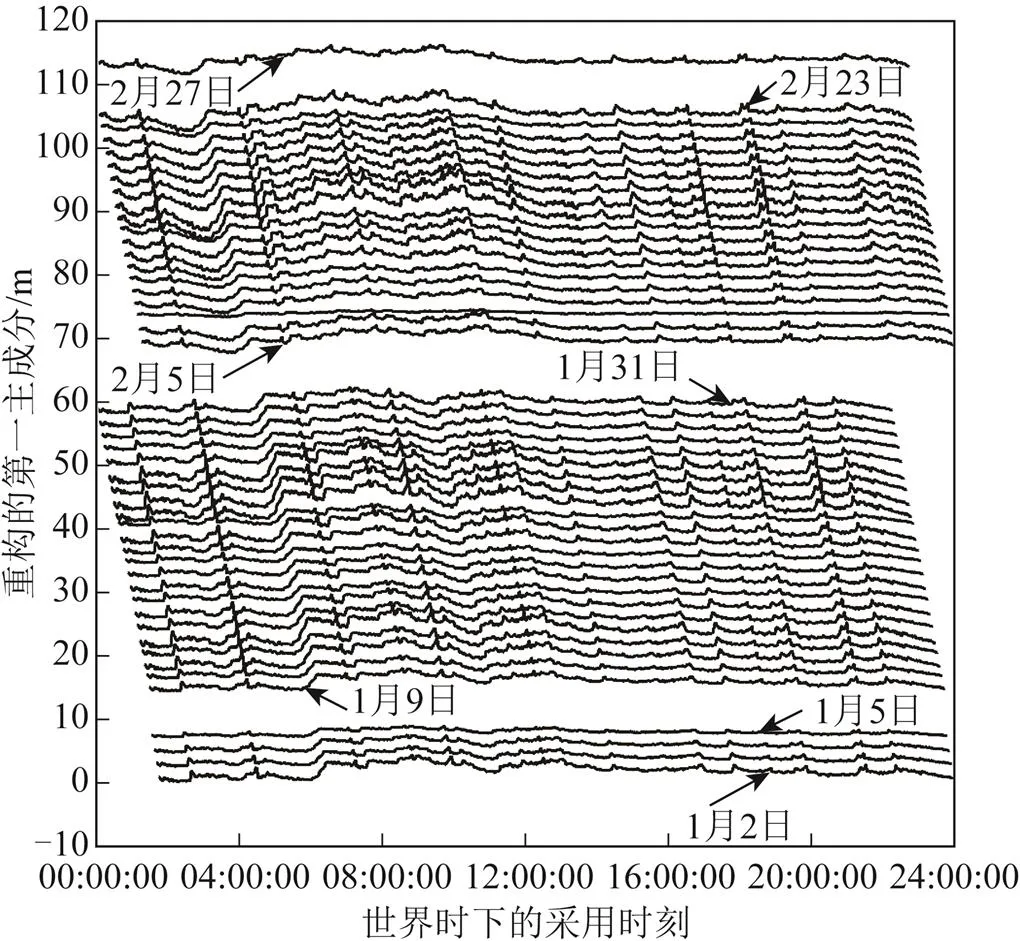
图6 1月份和2月份的重构的第一主成分

4 结果分析

为了验证这个方法的可靠性，将结果与用前人的研究方法得到的结果比较。前人通过伪距和载波相位的线性组合，来评估伪距的多路径误差[8,23]。该方法忽略载波相位的多路径误差和观测噪声，利用线性因子的组合将星站距离等项消除，得到伪距中的多路径误差和观测噪声。此处将前人方法得到的伪距的多路径误差和观测噪声称评估值。与评估值相比，通过主成分分析法得到的重构的第一主成分不含观测噪声，仅包含多路径误差。然而，重构的第一主成分分布在-2 m到3m之间，而评估值分布在-0.5 m到0.5 m之间（图7）。重构的第一主成分是评估值的4到5倍。这表明在重构的第一主成分中，除了多路径误差这个日重复项，还包含了其他日重复项。

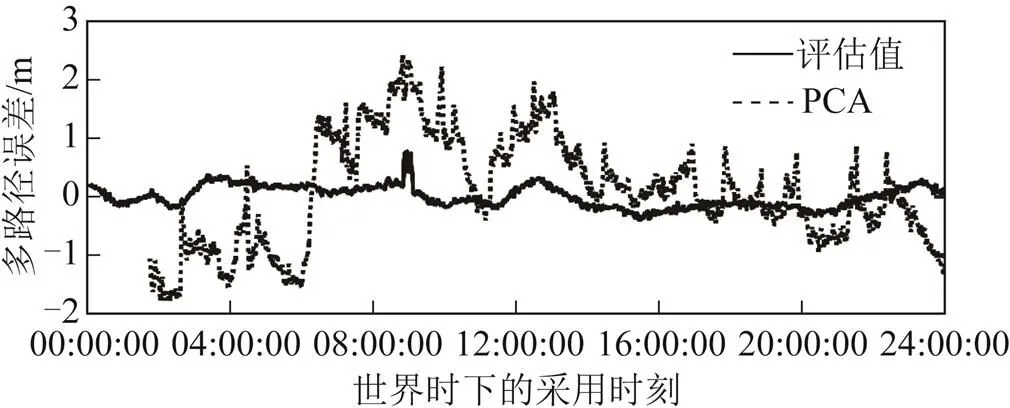
图7 比较两种方法的结果

由于对流层延迟和观测噪声的随机性大，可排除这二者是日重复项的可能。在包含多路径误差、对流层湿延迟、观测噪声的残差数据中，还可能包含之前扣除掉的物理量的残留项。根据重构的第一主成分的数值变化幅度以及在2个月内会重复出现的特征，可排除钟差、硬件延迟、对流层延迟和电离层延迟的残差项的影响。而星站距离的残留项有可能与日重复项有关。其中，星站距离的残留项包含卫星和台站天线的相位中心偏差和相位中心变化，以及台站和卫星的坐标与真实坐标之间的偏差。其中，天线相位中心偏差属于系统偏差，可当作固定值[24]。卫星和台站天线的相位中心变化不会超过10 cm[25]。台站坐标与真实值的偏差为常值，而通过插值后的卫星坐标与真实坐标的偏差，有可能是日重复项。

如果重构的第一主成分中的日重复项主要是由卫星坐标与真实坐标的偏差引起，则在中国香港地区的17个台站都应有相似的情况。由于大部分台站缺少气象观测数据，以下研究将伪距减去星站距离、电离层延迟、钟差和硬件延迟，再减去多路径误差和观测噪声的评估值，从而得到包含对流层延迟的残差数据。图8展示了HKOH台站2018年1月的包含对流层延迟的残差数据（图8中每天数据经过纵向3 m等间距平移）。

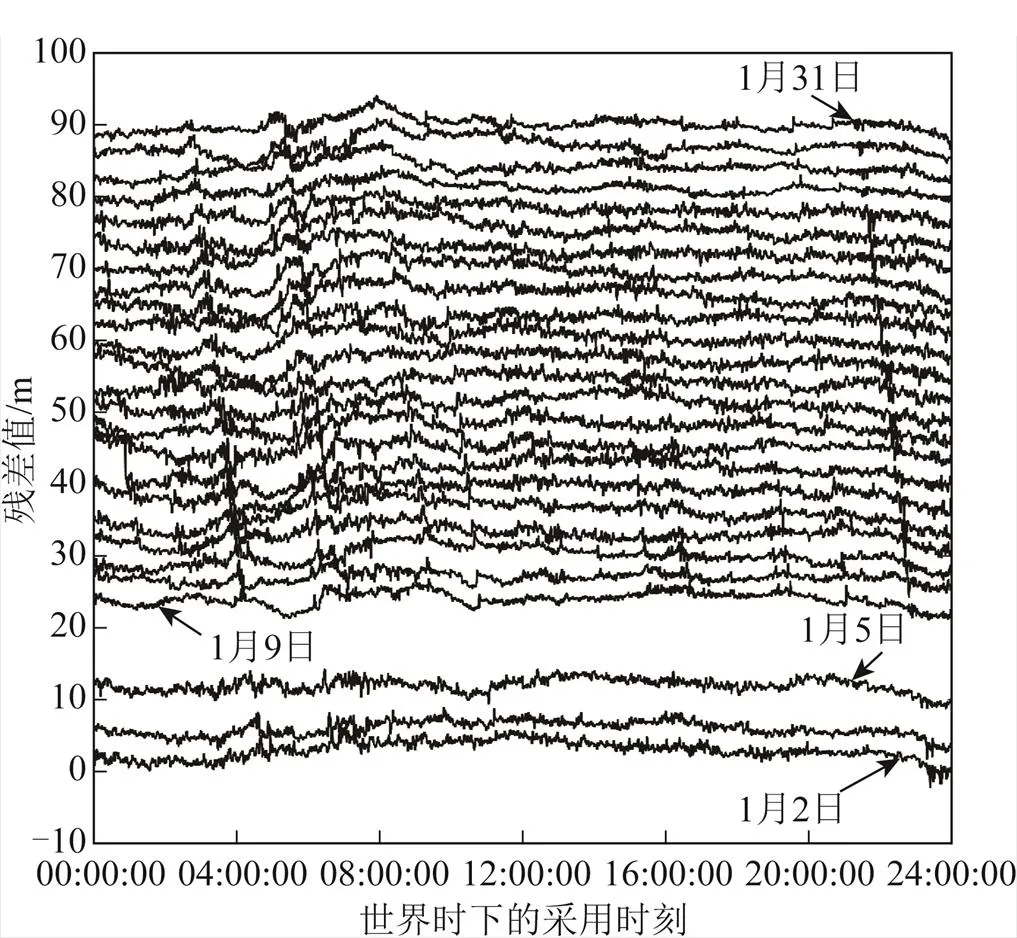
图8 2018年1月的包含对流层延迟的残差数据

重构的第一主成分中除多路径误差之外的日重复项亦存在于该残差数据中。每天的残差数据的变化幅度在4 m左右，而对流层延迟一天变化在分米级。因此，残差值的大部分为该日重复项。依旧以BDS C03同步卫星的B1频段伪距信号作为研究对象，对2018年每天任意两个台站的包含对流层湿延迟的残差数据做皮尔逊（Pearson）相关性分析[26]。在数据齐全的情况下，任意两个台站每天都可计算出一个相关系数。表2为17个台站中任意两个台站在2018年内相关系数的中位数，用于反映不同台站之间残差数据中日重复项的相关程度。

使用同为天宝的主机和天线的HKCL、HKTK、HKLM和HKQT台站之间的相关系数基本大于0.40（表2中浅灰色部分）。使用同为徕卡的主机和天线的11个台站，它们相互之间的相关系数基本分布在0.80到0.92之间（表2中深灰色部分）。然而，使用同为徕卡的主机和天线的台站与使用同为天宝的主机和天线的台站之间的相关系数基本分布在0.20左右。这表明包含对流层延迟的残差数据中的日重复项在使用相同类型的主机和天线的台站之间的相关系数，大于使用不同类型的主机和天线的台站之间的相关系数。另外，在图9（a）中，使用徕卡主机和天宝天线的T430台站与使用同为徕卡的主机和天线的台站的相关系数的中位数为0.87，而T430台站与使用同为天宝的主机和天线的台站的中位数为0.23。在图9（b）中，HKKS台站于年积日（day of year, DOY）第149天将天宝主机更换为徕卡主机。在更换主机前，HKKS台站与其他使用天宝主机的台站的相关系数的中位数为0.84，更换后相关系数降低为0.17。而与使用徕卡主机的台站的相关系数的中位数在更换接收机后明显变大，从原来的0.24变为0.93。上述结果表明，使用相同类型的主机的台站的日重复项相关性更高，且与接收天线无关。

表2 任意两个台站在2018年内相关系数的中位数

注：表身中省略另一半重复的数值。

图9 与其他16个台站的相关系数

如果日重复项是卫星坐标与真实坐标的偏差，则17个台站之间的相关系数应处于同一水平，而不是使用相同类型的主机的台站的相关性更高。故日重复项并非由卫星坐标与真实坐标的偏差引起的。基于使用相同类型的主机的台站的日重复项相关性更高的情况，本研究推断包含对流层延迟的残差数据中的日重复项与接收机主机类型有关。由于每个接收机主机的钟差是独立的，故不能引起上述结果。其可能是由于不同类型的接收机主机在处理信号的过程中的差异导致，为与接收机主机相关的系统误差。

5 结束语

本研究对中国香港地区GNSS台站接收的BDS C03同步卫星B1频段伪距信号进行处理，得到包含多路径误差、对流层湿延迟、观测噪声的残差数据，再利用主成分分析法从数据中提取每天重复出现的多路径误差。从HKOH台站2018年1月和2月的数据中，提取的第一主成分在重构后每天重复出现，为伪距中的日重复项，符合多路径误差的特征。

然而，当将重构的第一主成分与前人研究比较时发现，重构的第一主成分的大小是前人研究的4～5倍。这可能是由除了多路径误差之外的日重复项引起。本研究通过数值变化及重复出现的特征，排除了对流层延迟、电离层延迟、钟差和硬件延迟为该日重复项的可能性，并对星站距离残留项进行检验。本研究通过对中国香港地区的17个台站的残差数据做相关性分析，验证星站距离残留项对17个台站的影响是否相似。结果发现，使用同一类型的接收机主机的台站之间的日重复项呈现高度相关，而使用不同类型的接收机主机的台站之间的日重复项的相关系数比前者小，而且该结果与接收天线的类型无关。相关性分析的结果表明，日重复项与星站距离的残留项无关，而是与接收机主机类型有关。该日重复项可能是与接收机主机相关的系统误差。

致谢：感谢中国香港卫星定位参考站网和德国地球科学研究中心提供的数据。

[1] HÅKANSSON M, JENSEN A B O, HOREMUZ M, et al. Review of code and phase biases in multi-GNSS positioning[J]. GPS Solutions, 2017, 21(3):849-860.

[2] 李政航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2016:79-82.

[3] KLOBUCHAR J A. Ionospheric time-delay algorithm for single frequency GPS users[J]. IEEE Transactions on Aerospace and Electronic, 1987, 23(3): 325-331.

[4] HOPFIELD H S. Two-quartic tropospheric refractivity profile for correcting satellite data[J]. Journal of Geophysical Research, 1969, 74(18):4487-4499.

[5] GEORGIADOU Y, KLEUSBER A. On carrier signal multipath effects in relative GPS positioning[J]. Manuscripta Geodaetica, 1998, 13(3):172-179.

[6] 张波, 黄劲松, 苏林. 利用信噪比削弱GPS多路径效应的研究[J]. 测绘科学, 2003, 28(3):32-35.

[8] KLEUSBERG A, TEUNISSEN P. GPS for geodesy[M]. New York: Springer-Verlag, 1996:156-160.

[9] HAN S W, RIZOS C. GPS multipath mitgation using FIR filters[J]. Survey Review, 2000, 35(277):487-498.

[10] GE L, HAN S, RIZOS C. Multipath mitigation of continuous GPS measurements using an adaptive filter[J]. GPS Solutions, 2000, 4(2):19-30.

[11] 黄丁发,丁晓利, 陈永奇, 等. GPS多路径效应影响与结构振动的小波滤波筛分研究[J].测绘学报, 2001, 30(2):36-41.

[12] ZHONG P, DING X L, ZHENG D W, et al. Adaptive wavelet transform based on cross-validation method and its application to GPS multipath mitigation[J]. GPS Solutions, 2008, 12(2):109-117.

[13] 王青平, 关玉梅, 王紫燕, 等. GPS卫星轨道三维坐标插值算法比较[J]. 地球物理学进展, 2014, 29(2):573-579.

[14] 周佩元, 杜兰, 路余, 等. 多星定轨条件下北斗卫星钟差的周期性变化[J].测绘学报, 2015，44(12):1299-1306.

[15] WILSON B D, MANNUCCI A J. Instrumental biases in ionospheric measurements derived from GPS data[C]//The Institute of Navigation (ION).Proceedings of the 6th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake City: ION, 1993:1343-1351[2021-01-18].

[16] XUE J, SONG S, ZHU W. Estimation of differential code biases for Beidou navigation system using multi-GNSS observations: how stable are the differential satellite and receiver code biases?[J]. Journal of Geodynamics, 2016, 90(4):309-321.

[17] ELGERED G, DAVIS J L, HERRING T A, et al. Geodesy by radio interferometry: water vapor radiometry for estimation of the wet delay[J]. Journal of Geophysical Research, 1991, 96(B4): 6541-6555.

[18] 曲建光, 魏旭东, 王泽民, 等. 在高海拔地区Saastamoinen与Hopfield模型推算水汽含量差异的研究[J]. 武汉大学学报(信息科学版), 2003, 28(4):397-399.

[19] SAASTAMOINEN J. Atmospheric correction for troposphere and stratosphere in radio ranging of satellites[C]// American Geophysical Union (AGU). Proceedings of the Use of Artificial Satellites for Geodesy. Washington: AGU, 1972, 15:247-251[2021-01-18].

[20] BOEHM J, NIELL A, TREGONING P, et al.Global mapping function (GMF): a new empirical mapping function based on numerical weather model data[EB/OL].[2021-01-18].http://rses.anu.edu.au/geodynamics/gps/papers/boehms_ GMF.pdf.

[21] 华爱辉. 机动情况下的GEO卫星定轨方法研究[D]. 西安: 中国科学院研究生院(国家授时中心), 2008.

[22] 冯帅, 李亮, 程春, 等. 北斗空间信号误差统计特征及描述方法研究[J].导航定位与授时, 2019, 6(3):95-102.

[23] WANG G X, ZHAO Q L, HU Z G, et al. Multipath analysis of code measurements for BeiDou geostationary satellites[J]. GPS Solutions, 2015, 19(1): 129-139.

[24] GU D F, LAI Y W, LIU J H, et al. Spaceborne GPS receiver antenna phase center offset and variation estimation for the Shiyan 3 satellite[J]. Chinese Journal of Aeronautics2016, 29(5): 1335-1344.

[25] SCHMID R, ROTHACHER M, THALLER D, et al. Absolute phase center corrections of satellite and receiver antennas[J]. GPS Solutions, 2005, 9(4): 283-293.

[26] BENESTY J, CHEN J, HUANG Y. Pearson correlation coefficient[M]//BENESTY J, KELLERMANN W. Noise reduction in speech processing. Berlin: Springer Nature Switzerland AG, 2009: 37-38[2021-01-18].

Daily repetition variations in pesudorange signals from ground-based GNSS receivers

ZHANG Dixin1, CHEN Chiehhung1, SU Xiaoning2, SUN Yangyi1, LIN Kai1, XU Rui3, MENG Guojie4, YEH Takang5

（1.Institute of Geophysics and Geomatics, China University of Geosciences (Wuhan), Wuhan 430074, China;2.Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China;3.Earthquake Administration of Sichuan Province, Chengdu 610041, China;4.Institute of Earthquake Forecasting, Key Laboratory of Earthquake Forecast, China Earthquake Administration, Beijing 100036, China;5.Department of Real Estate and Built Environment, Taipei University, New Taipei 23741, China）

Multipath error are daily repetition variations, which appear in pesudorange every day. A filtering algorithm is a typical and efficient strategy to extract the multipath errors from the pesudorange signal. However, the straightforward method gets struggling if the frequency of multipath errors and noises are unknown or mixed up. This study attempts to propose a new technology to figure out this problem. We extract the multipath error from residual data by applying the principal component analysis. It should be noted that residual data containing multipath errors, tropospheric wet delay and noises, are obtained by pesudorange eliminating the distance between a satellite and a station, clock errors, hardware delay, ionospheric delay and tropospheric hydrostatic delay. Reconstructed first principal components obtained by principal component analysis have periodic characteristics called daily repetition variations, and they are multipath error theoretically. However, its value is 4 to 5 times bigger than previous studies. It indicates that there are other daily repetition variations besides multipath errors in pesudorange signals. We analyzed the data from 17 stations, and results show that the correlations of this daily repetition variations are higher among stations using the same type of receiver host. It suggests that the daily repetition variations in the pseudorange signals are associated with the type of receiver host, and it probably is a system error related to the receiver host.

multipath error; daily repetition variations; principal component analysis; receiver host

P228

A

2095-4999(2022)01-0076-09

张帝鑫，陈界宏，苏小宁，等. 地基GNSS接收伪距信号中的日重复项[J]. 导航定位学报, 2022, 10(1): 76-84.（ZHANG Dixin, CHEN Chiehhung, SU Xiaoning, et al. Daily repetition variations in pesudorange signals from ground-based GNSS receivers[J]. Journal of Navigation and Positioning, 2022, 10(1): 76-84.）

10.16547/j.cnki.10-1096.20220111.

2021-03-01

国家自然科学基金委联合基金项目（U2039205）。

张帝鑫（1995—），男，广东惠州人，硕士研究生，研究方向为地基GNSS接收机的多路径误差。

陈界宏（1977—），男，台湾台北人，博士，教授，研究方向为震前多物理参量耦合。