基于KOPLS的多组分物质光谱分析方法

皮世威，林 朝，黄哲学

(1.深圳大学 计算机与软件学院，广东 深圳 518060;2.深圳市理邦精密仪器股份有限公司，广东 深圳 518067)

0 引言

在化学测量领域中，多组分物质的浓度光学测量是研究经典问题，其分析方法被广泛应用于临床检验中，对于医学判定和辅助诊断具有重要的作用。由于生物样本的复杂特性，化学计量的信号具有高噪声[1]、多重叠[2]、特征变量多的特点[3]，分析过程中包含大量的非线性拟合过程[4]，通常需要应用大量的回归分析来建立因变量与自变量之间的非线性关系。当前化学计量最常应用的回归方法有普通最小二乘(OLS)[5]，偏最小二乘法(PLS)，正交偏最小二乘法(OPLS)[6]等，其中普通最小二乘是经典的拟合方法。偏最小二乘回归线性拟合对于独立自变量多于因变量的案例具有较好的回归应用效果，可以有效剔除高维度变量中的无关成分[7]。正交偏最小二乘法(OPLS)[8]是在偏最小二乘的基础上通过建立自变量的正交映射，能够更为高效的去除变量中的无关信息，在迭代求解残差项中的正交量过程中，快速提取有效信息，对于复杂背景噪声下的变量具有明显的主成分提取作用，正交偏最小二乘法在代谢组以及化学分析领域中具有广泛的应用[9-10]，但该方法对于多变量应用下易发生过拟合现象，导致预测精度降低。文献[11]在OPLS拟合的基础上，通过引入Kernel核变量将原空间中的正交成分转化到特征空间，在高维空间完成正交无关项的预测与分离，该方法能够提升变量的非线性拟合精度，提高多变量的预测能力。Kernel矩阵对于非线性拟合具有较高的拟合精度[12]，并且对于分析过程中的分类方式具有较好的可视化特性。KOPLS(核正交偏最小二乘法)的非线性拟合优势被应用于代谢组[13-14]和多组分浓度光谱分析中。尤其在多组分物质浓度测量中，由于被测样本成分复杂，光谱信号往往包含非线性噪声和干扰[15]，高精度的光谱分析建模方法成为预测准确度控制的重要因素。

1 建模方法

在多组分物质光谱分析应用中算法的核心思想是建立原数据矩阵X和浓度矩阵Y之间的映射模型。在保证模型准的预测准确度的前提下，同时还需要具有较快的计算速度。常用的建模算法有偏最小二乘(PLS)、正交投影映射(OPLS)等。

1.1 PLS算法

偏最小二乘法PLS的核心思想是最大化自变量与因变量数据之间的协方差来解析自变量中的正交得分向量，首先对原数据矩阵X和浓度矩阵Y进行主成分分析：

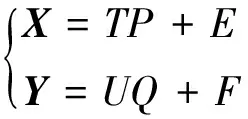
(1)

主成分个数由权重项w决定，分解得到各自对应的得分矩阵T、U和载荷矩阵P、Q，残差项分别为E、F。通过主成分分析T=XP,可以将原数据矩阵和浓度矩阵分别降至相应的低纬度空间，并保留原矩阵中的大部分有效信息。再对建立各自得分矩阵之间的线性回归方程：

U=TB

(2)

B为回归系数矩阵。

B=TU(TTT)-1

(3)

最后X相对与Y的线性回归可转变为X得分矩阵相对于Y的线性回归：

Y=TBQ

(4)

步骤1～6为标准的NIPALS PLS法

1.w=max;

2.w=w/‖w‖;

3.t=Xw/(wTw);

4.qT=tTY/(tTt);

5.u=Yc/(cTc);

6.pT=tTX/(tTt);

1.2 OPLS方法

OPLS是在PLS的基础上建立的，通过筛选原数据矩阵X与浓度矩阵Y的不相关信息，使分类信息快速集中在主成分中，从而搭建简洁的X与Y的线性关系，这种建模方法适用于多元数据统计，OPLS建模的具体步骤如下。首先和PLS一样，通过主成分分析法建立X、Y的线性组合：

(5)

(6)

其中：t，u可由权系数w，c求得：

t=Xw/‖w‖

(7)

u=Yc/‖c‖

(8)

为使t、u之间的相关性最大，可以目标化t、u的协方差为最大，即：

Max:Cov(t,u)

(9)

采用拉格朗日方法求解极值问题，w为XTYYTX矩阵的最大特征值对应的特征向量，c为YTXXTY矩阵的最大特征值对应的特征向量。随之即可求相应的得分向量t，u。这样X和Y的载荷矩阵可通过关系式求得：

pT=tTX/(tTt)

(10)

qT=uTY/(uTu)

(11)

计算X的正交权重向量worth：

worth=p-[wTp/(wTw]w

(12)

worth=worth/‖worth‖

(13)

那么X正交矩阵的得分向量：

(14)

X正交矩阵的载荷：

(15)

求解正交残差项EOPLS、FOPLS：

(16)

将X替换为EOPLS因此则有：

(17)

再对Xorth进行主成分分析：

(18)

由式(4)可将X相对与Y的线性回归可转变为得分矩阵Xorth相对于Y的线性回归。相对于PLS，OPLS能够对系统变量进行单独分析，通过去除正交无关量，可以降低过拟合发生的现象。但是当变量之间差异性较小，非线性耦合程度较高时，差异变量无法有效的被剔除，此时OPLS模型的计算准确度会降低。

1.3 基于K-OPLS的多组分物质分析方法

KOPLS在OPLS算法的基础上保留了正交无关项的理念，并对建模方法做了进一步的改进，通过引入Kernel核矩阵来对数据中的非线性结构进行建模，同时仍可像OPLS一样对数据中的无关项进行筛选。在KOPLS算法中，通过对预测成分Tp和正交成分Yorth的建模来有效提取数据中的相关成分，这使得KOPLS模型的预测精度与基于核矩阵的偏最小二乘法(KPLS)[16]以及支持向量机模型[17]的预测精度保持一致，但Kernel矩阵通过在高维度的特征空间内对信号中的噪声进行转换建模，能够有效的消除原数据中由于外界因素带来的异常信息，例如测量仪器的信号漂移、样本中的生物耦合变量等。因此KOPLS对于非线性因素影响较大的生物化学多组分析具有较高的估算精度。

在KOPLS具体算法中，Kernel矩阵的引入将原矩阵X中的变量转化为高维特征空间内的点积(XXT)，接着通过将XXT替换为Kernel矩阵K，Kernel矩阵K中的元素Ki,j由X的第i和第j行向量组成，Kernel变换通过简洁的计算方式在将X映射到了高维空间中。因此KOPLS算法的第一步是选择合适的核函数，常用的核函数有线性、多项式和高斯核函数，其表达式分别为：

k(x,y)=x×y

(19)

k(x,y)=(xTy+1)P

(20)

k(x,y)=exp(-‖x-y‖2/2σ2)

(21)

接下来的步骤是将原数据矩阵替换为核矩阵具体计算步骤如下。

①Kernel矩阵中心化:

KOPLS算法往往用于处理维度较大的数据，因此首先需要对Kernel矩阵进行中心化处理，中心化计算方法：

(22)

式中,En为n×1的向量，元素等于1。

②求解权重向量:

建立Kernel矩阵K后，需确定数据中的正交成分个数N。这样K表示为被剔除第N个正交成分后所组成的矩阵。接着通过对YTKY特征值分解求得权重向量Cp和∑p。

③求Y预测得分矩阵：

通过将Y映射到Cp上可求得Y的预测得分矩阵：

Up=YCp

④求X预测得分矩阵:

X的预测得分矩阵:

Tp=KTUp∑p(-1/2)

⑤在正交成分个数1到N内，迭代循环：

对TpTQiTp特征值分解，求得Y正交载荷向量Corth；

计算Y正交得分向量t(orth-i)=QiTpCorth。

⑥对torth抽取Ki，得到Ki+1；

此时预测得分矩阵:

Tp=K(i+1)Up∑p(-1/2)

⑦最后建立回归方程：

KOPLS算法在预测项远大于测量项的应用下，具有较好的预测准确度，因此在非线性回归和分类应用较多的组分学中，KOPLS的优势较为明显。例如对于使用光谱吸光度信号对样本中的多组分物质浓度分析时，样本本身复杂的络合状态往往伴随较大的非线性信号结构，KOPLS中特有的将Y预测成分与正交无关成飞在特征空间中分离步骤，相对于OPLS和PLS都具有更好的预测执行能力。

KOPLS在代谢组学研究中已有成功的应用。而对于多组分物质光谱分析应用场景，需要通过算法拟合建立光谱与各组分物质浓度之间的非线性关系，由于需要从单个光谱中解析的多组分物质较多，而各组分之间特征耦合度高，且存在较多的非线性关系，KOPLS的特点正好适用于此类场景的建模，模型拟合效果相对于OPLS和PLS更好。

2 实验结果

为了对比各算法在多组分物质光谱分析中的应用优劣，通过对多组分物质的浓度分析实验来评估。实验用多组分物质采用血液中的血红蛋白及其衍生物为样本。其测量方法基于分光光度法[18]，即由于多组分物质中各物质的吸收波长各不相同，因此根据朗博比尔定律：

A=k1c1l+k2c2l+…+kncnl

(23)

其中：A为总吸光度系数;ki为各组分物质的吸光度系数;ci为各组分物质的浓度;l为测量光学量程。

由此可知对于不同浓度下的衍生物，其总吸光度也各不同，通过建立吸光度曲线与各组分物质浓度之间的关系，即可实现通过测量吸光度来完成对多组分物质的浓度检测，如图1所示。

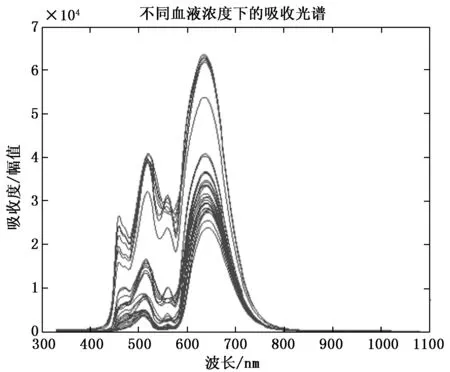
图1 不同血液样本浓度下的吸收度光谱曲线分布图

实验首先通过200组数据进行建模，为保证原始数据的准确性，每组样本的光谱信号采用海洋光学光谱仪(QE65 Pro)进行采集，对样本数据搭建基于PLS，KOPLS模型的吸光度-多组分物质浓度的分析模型。再通过111组样本和靶标带入模型中进行计算，通过对比各自算法下的预测值与靶标值的差异，如图2所示。

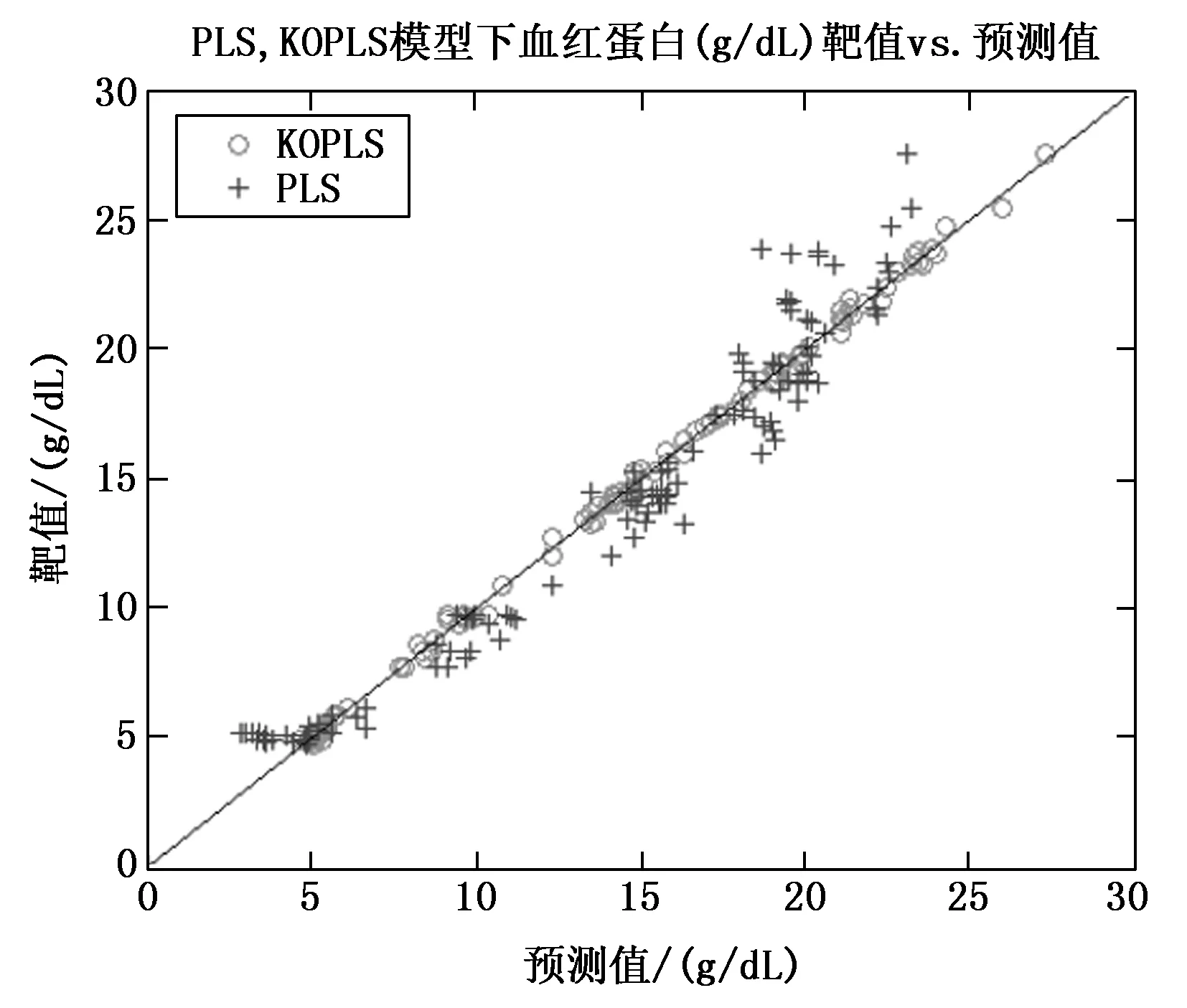
图2 PLS, KOPLS模型下的血红蛋白浓度预测结果对比

从计算结果图2可以看出，当采用PLS算法进行建模时，血红蛋白浓度预测值相对靶值的准确度达到±5.2 g/dL，在高浓度区间时，预测结果的离散度增大，这是由于被测样本为血液，其物质组成复杂，光谱分析过程包含过多的非线性因素。当采用KOPLS算法建模时，设定迭代剔除正交无关项20次，预测值相对靶值的准确度达到±0.6 g/dL，准确度得到较大的提升。对比结果如表1所示，实验结果说明KOPLS对于非线性因素较多的血液样本单一物质浓度分析具有较高的预测精度。

表1 PLS, KOPLS模型下的血红蛋白

对于血红蛋白中多组分物质浓度测量，光谱数据中各组分对应的特征量存在部分重叠。在建模过程中需要在不同血红蛋白浓度下配置不同梯度的多组分衍生物浓度。建模过程采用PLS模型和KOPLS模型，在两种模型下分别对111组样本进行预测，预测精度对比如图3所示。

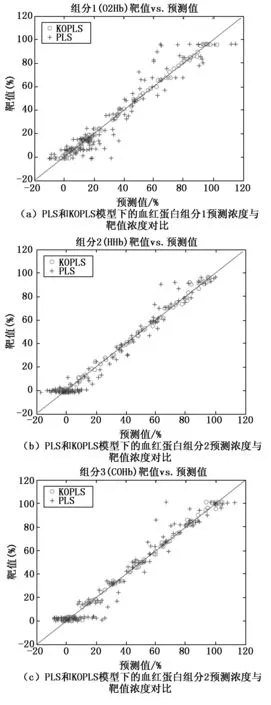
图3 PLS, KOPLS算法建模下的多组分物质浓度预测结果对比

从计算结果图3(a)以看出，当采用PLS算法进行建模时，血红蛋白组分1的浓度预测值相对靶值的准确度达到±32.6%，各梯度区域预测结果的离散度较大。当采用KOPLS算法建模时，预测值相对靶值的准确度达到±6.6%，准确度得到较大的提升，在不同梯度下的离散度也有了很大的降低。血红蛋白组分2的浓度预测值相对靶值的准确度达到±26.7%，结果如图3(b)所示，各梯度区域预测结果的离散度同样较大。当采用KOPLS算法建模时，预测值相对靶值的准确度达到±9.3%，准确度得到了较大的提升，在不同梯度下组分2的离散度也有了大幅提升。血红蛋白组分3的浓度预测值相对靶值的准确度如图3(c)所示达到±34.5%，各梯度区域预测结果的离散度较大。当采用KOPLS算法建模时，预测值相对靶值的准确度达到±9.48%，准确度和离散度同样得到较大的提升，对比结果如表2所示。对比结果说明KOPLS对于预测血液样本中的多组分物质浓度具有较高的预测精度，测量结果相对于PLS有明显的提升。

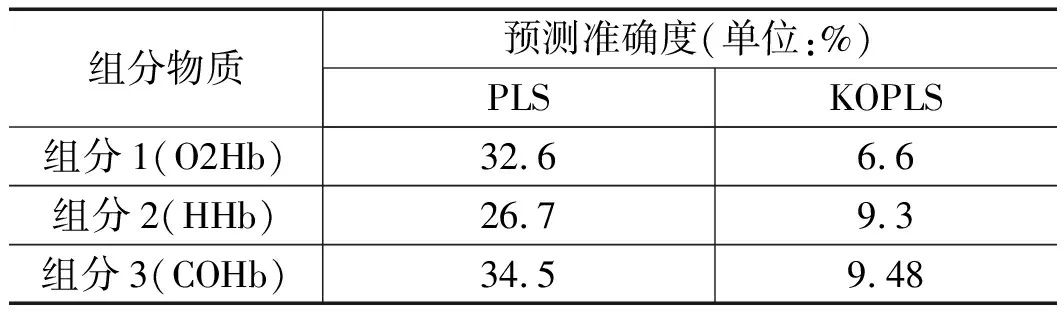
表2 PLS, KOPLS模型下的血液多组分物质浓度预测准确度

3 结束语

本研究通过算法推导阐述了由PLS到OPLS，再到KOPLS算法的演变过程。KOPLS算法保留OPLS的正交映射思想，通过剔除正交无关量，快速提取原数据矩阵中的有效特征，建立原数据与变量之间的映射关系。同时通过Kernel变换，将原数据矩阵转化为高维特征空间的内积，建立原数据与变量之间的非线性关系。通过对血液样本的吸收光谱和多组分物质浓度进行KOPLS建模于预测计算，结果表明KOPLS对于具有大量非线性关系的血液多组分物质浓度分析具有明显的预测优势。这些特点可以在多组分物质浓度检测设备中得到应用。