杂波信息未知下的多群目标跟踪算法
张琪,马天力,陈超波,张彬彬
(西安工业大学 电子信息工程学院,陕西 西安710021)
0 引言
由于现代战争的任务复杂以及杂波信息未知,无人机系统朝着集群化方向发展,其目的是有效解决有限空间内多无人机之间的对抗问题。对于无人机集群的跟踪,其目标是对群整体运动特征和空间形状进行估计,然而无人机集群机动性强,形状难以辨别,且群结构随目标运动可能发生分裂和合并,特别是在杂波信息未知的高杂波环境下,如何对无人机集群进行准确地跟踪已成为一个亟需解决的问题。
针对多群目标的运动状态估计,目前主要方法可分为两种:一种是传统的数据关联多群目标跟踪方法,该方法首先通过量测-目标关联,然后利用贝叶斯滤波方法将多群目标跟踪问题转化为多个单目标跟踪问题,典型算法包括联合概率数据关联算法、概率多假设跟踪算法和联合概率强度滤波算法。该方法的关键点在于数据关联,错误的关联会导致跟踪性能变差,甚至出现目标漏跟,并且随着目标数目以及杂波密度的增加,数据关联容易产生组合爆炸问题。另一种是基于随机有限集理论的多群目标跟踪方法,其通过随机有限集对所有的目标状态和量测进行描述,并利用贝叶斯滤波方法估计出多群目标的数目和状态。其中,文献[5]提出了基于随机矩阵的高斯逆威沙特概率假设密度(Gaussian Inverse Wishart Probability Hypothesis Density,GIW-PHD)滤波器,分别用高斯分布和逆威沙特分布对群目标运动状态以及扩展状态进行建模。文献[6]在椭圆形随机超曲面理论的基础上对高斯混合PHD滤波算法进行了扩展。但PHD滤波器易受到杂波或虚警的干扰,造成势估计偏差较大,从而导致目标数估计出现波动。因此,Orguner提出了扩展目标势概率假设密度(Cardinalized PHD,CPHD)滤波器。基于此,文献[8]提出了基于星凸随机超曲面模型的扩展目标伽马高斯混合CPHD滤波器,对不规则的形状边界进行约束优化。文献[9]提出了-CPHD滤波器,准确地提取群目标状态。但PHD滤波器和CPHD滤波器无法直接估计目标运动轨迹,且存在权重转移的“幽灵效应”。故文献[11]提出加标高斯逆威沙特多伯努利(Generalised Labelled Multi-Bernoulli,GLMB)滤波器,并表明ET-GLMB可估计群目标轨迹。在上述滤波器的基础上,文献[12]利用泊松多伯努利混合共轭先验形式,将目标集分割为两个独立不相关的子集(目标已被检测和未被检测),其中多伯努利混合项表示目标间可能存在的数据关联。多伯努利滤波器中各目标独立同分布且分布可不同,因此不易受到“幽灵效应”的影响。在整体上直接近似递推目标状态的后验概率密度,但对目标数存在较为严重的过估。文献[14]提出基于星凸形随机超曲面模型多扩展目标多伯努利滤波器,该方法可对多个群目标的目标数进行精确估计。但上述基于随机有限集的滤波算法需要满足杂波密度服从均匀分布、杂波数目服从泊松分布、新生目标强度和检测概率先验已知等许多假设条件,而在实际应用过程中,通常难以准确获得杂波以及新生目标的先验信息,一旦真实条件与假设模型不一致,就有可能导致跟踪性能变差甚至丢失目标。
针对先验信息未知的高杂波环境下对多群目标跟踪容易出现跟踪失败的问题,本文提出了基于网络流理论的多群目标跟踪方法。该方法通过改进的谱聚类算法进行量测分割,根据分割后所得量测集合构建多群目标网络流模型,采用A搜索算法求得多约束条件下最小代价网络流问题的全局最优解,再对所提取到的多个航迹进行优化整合,最终得到多条群目标航迹。
1 问题描述
假设多群目标={,,…,s},为目标数,令每个群目标在时刻的状态向量为:

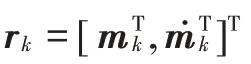
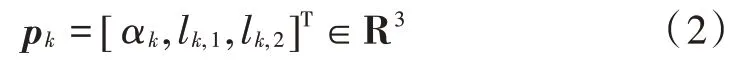
式中:α∈[0,π 2],为时刻的椭圆方向;l,l∈R是椭圆半轴长度。
1.1 量测模型
假设在时刻,一个群目标产生M 个相互独立的二维量测:

则量测方程可表达为:






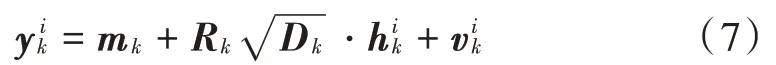
1.2 动态模型
假设群目标的运动状态和形状参数是相互独立的,并遵循如下的线性马尔可夫模型:


2 基于网络流多群目标跟踪算法
在杂波信息不确定的条件下,传统的多群目标跟踪算法会出现目标丢失的现象,导致目标跟踪性能下降。针对群目标结构可能会发生分裂和合并的问题,本文提出了一种基于网络流多群目标跟踪方法,将多群目标的数据关联问题转化为一个代价流网络优化问题,利用A搜索算法求解最小代价网络流问题的最优解,对提取的多条航迹进行优化整合。
2.1 基于自适应谱聚类算法的量测分割
在判断群整体的结构信息是否发生变化之前,需要将具有相似运动模式的多个点目标归纳为一个群目标,于是只需考虑群质心的运动信息来降低计算复杂度。因此需要正确地划分出单位时间内群目标的数量。

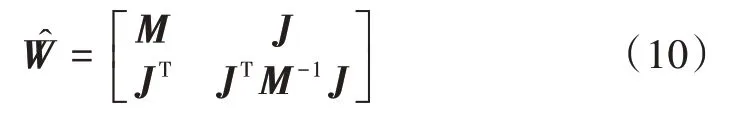



2.2 多群目标最小代价网络流模型


式中(T)为马尔科夫链模型。条航迹的概率为:

则式(13)的最大后验概率为:
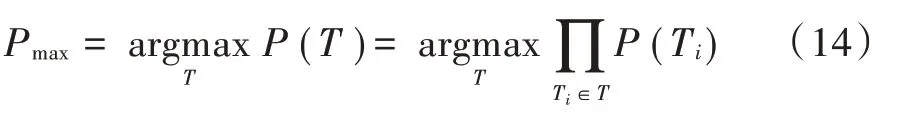
其log似然形式如下所示:
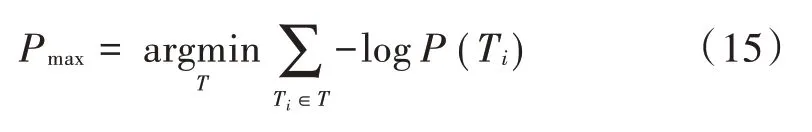
最小代价网络流模型为该目标量测集合建立一个带有唯一源点和唯一汇点的带权有向图(,),其中,=(,,…,v)为节点组成的集合,为每个有向边组成的集合,如图1所 示。每 一 量 测ˉ对应网络中的一个节点v。

图1 最小代价网络流结构示意图
网络中节点间的有向边包括:

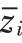
根据上述网络构建方式,多群目标的航迹可以转化为以最小总代价在网络中从源点向汇点发送一定数量的流。具体地,流经过的边的总代价定义为:
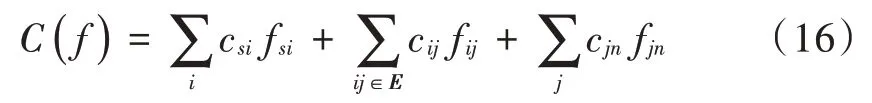
每一条流经过的路径将集合中具有时空一致性的量测连接在一起,因此可表示为一条有效的目标航迹。为满足多群目标跟踪过程中的实际物理约束,因此网络中的流需要满足以下约束条件:
1)流保持约束。网络中所有节点的流入量应等于流出量,表示为:

2)边容量约束。流经网络中每条边的流量不能超过该条边的容量,而每条边上的流起选择作用,取值为0或1。因此,边容量约束表示为:

3)供应/需求约束。网络中的流皆起始于源点、终止于汇点,表示为:

在上述约束条件下最小代价网络流问题是一个NP完全的ILP问题,将式(14)的网络优化问题转化成整数规划问题:

式中:表示流的变量f,f和f的集合;0和1分别表示元素值全部为0和1的向量。对于上述问题,采用A搜索算法求得最优解,再根据随机矩阵理论得到群目标的运动状态向量x和扩展状态矩阵X,利用贝叶斯平滑算法提高估计精度。由时刻和+1时刻的量测数据计算出时刻的均值和协方差:

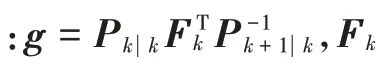
2.3 群目标结构优化
由于上述模型里的节点和有向边均不共享,即任意两条航迹对应的量测集合之间没有交集,这就有可能造成航迹的断裂,且提取到的航迹数往往不唯一。故采用一种群目标结构优化方法,在提取到的所有航迹中筛选出具有一定联系的若干条航迹(如目标运动速度一致,空间位置相离较近等),对这些航迹进行结构优化,其模型如图2所示。
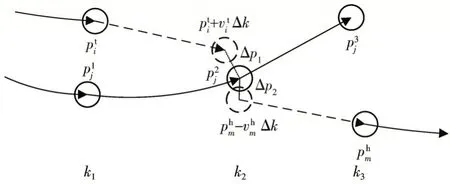
图2 群目标结构优化示意图
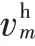
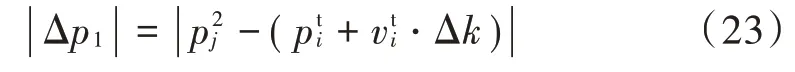


其预测位置与待关联位置的距离越小,与之相对应的航迹相关联的可能性越大,因此设置阈值表示航迹相关程度,若> ||Δ,则两航迹相关联,否则,两航迹无关。
3 仿真实验
为了验证本文所提基于网络流跟踪算法的有效性,选取高斯混合群目标概率假设密度滤波器(GM-GPHD)和本文算法进行比较,采用最优子模式分配(Optimal Sub-pattern Assignment,OSPA)距离作为评价标准。在仿真场景中,设目标周边的杂波个数服从均值为=20的泊松分布,以及全局的杂波个数服从均值为=5的泊松分布。假设群目标的扩展外形始终保持为椭圆外形且沿如图3所示的航迹在同一平面内运动,初始两个群目标以33 km/h的恒定速度运动,在第30时刻合并为一个群目标,在第62时刻分裂成3个群目标。每时刻量测结果均在椭圆内均匀产生,且量测数目遵循泊松分布,令量测噪声为协方差为R=0.6×diag{10,2}的高斯白噪声,采样周期=10 s。群目标的初始质心位置分别为[0,5.8×10]m和[0,-5.81×10]m。OSPA距离参数设为c=10,p=2。基于设定的仿真场景,采用本文所提算法和GM-GPHD滤波器对多群目标进行跟踪,分别进行100次独立的蒙特卡洛仿真实验以对比二者在群目标质心位置和目标数方面的估计性能以及算法的平均运行时间。

图3 目标真实运动场景
如图4所示,为两种算法对群目标位置估计的平均OSPA距离,从图中可以看出,本文算法对多群目标质心跟踪估计的OSPA距离小于GM-GPHD滤波器。此外,无论群结构是否发生分裂与合并,本文算法均有较低的OSPA距离,但GM-GPHD滤波器对群目标结构变化不敏感,尤其是在一个群目标分裂成3个群目标后,造成对于群目标的运动状态估计不精确,从而OSPA距离增大,因此本文算法在对多群目标的运动状态估计上优于GM-GPHD滤波器。

图4 本文算法和GM-GPHD滤波器对群目标位置估计的平均OSPA距离
如图5所示,可以看出与真实目标数目相比,本文所提算法能够准确估计目标数目。由于在群结构发生合并之前和发生分裂之后,各个群目标之间的位置关系并不是可明确分开,因此两种方法都将其视为一个群目标,一旦群目标之间有一定距离,本文所提算法就可以快速准确地估计出目标数目,而对于GM-GPHD滤波器,由于先验信息未知导致无法准确划分量测,所以在起始阶段和群结构发生变化时,都需要较长时间进行调整,造成估计的目标数目与真实目标数目误差较大。此外,如表1所示,本文所提算法的运行时间远小于GM-GPHD滤波器的运行时间,大大提高了计算效率。

表1 本文算法和GM-GPHD滤波器的平均运行时间 s

图5 本文算法和GM-GPHD滤波器的平均目标数估计
综合以上分析,本文算法能够针对复杂环境下的椭圆外形多群目标的目标数和运动状态进行准确的估计,与已有的GM-GPHD滤波器相比,本文算法在群结构发生分裂与合并时,既可以保证航迹提取的准确率,也具有相对较低的运算时间,展现出更加优越的性能。
4 结论
本文在采用椭圆的运动状态和形状参数对多群目标的量测源进行建模的基础上,提出一种最小代价网络流多群目标跟踪算法。在先验信息未知的高杂波且群目标结构发生分裂和合并的复杂跟踪环境下,分别通过对形状大小可能发生变化的多群目标的状态(包括运动状态和形状参数)进行估计,验证了所提算法的有效性。仿真结果表明,本文算法可同时对多群目标的运动状态、形状以及目标数进行较为精确的估计。总之,相比GM-GPHD滤波器,本文算法对目标数的估计更稳定,对目标质心的位置估计也更精确。

