基于改进的DBSCAN算法自动识别断层方法研究及其在唐山地区的应用

张苏祥 盛书中* 席 彪 房立华 吕 坚 王甘娇 张 潇

1)东华理工大学，地球物理与测控技术学院，南昌 330013 2)长江大学，油气资源勘探技术教育部重点实验室，武汉 430100 3)中国地震局地球物理研究所，北京 100081 4)江西省地震局，南昌 330039

0 引言

近年来，随着地震观测台网的不断加密和地震仪观测能力的提高，观测到的地震事件数剧增，定位的准确性也不断增加，为精细刻画断层构造提供了基础。大量基于震源空间位置分布获取深部断层构造的研究工作陆续发表(Ouillonetal.，2008； 万永革等，2008； Hayesetal.，2010； Wangetal.，2013； 盛书中等，2014，2015； Skoumaletal.，2019； Kameretal.，2020； Brunsviketal.，2021)。这些研究表明，从海量的地震数据中获取断层形态及其参数是发震构造研究的一个重要方法。当前基于地震资料获取断层及其参数的研究中，选取数据的方法主要有2类： 1)基于对断裂构造的认识以及地震数据空间分布情况经验性地选取地震数据，再由这些数据拟合出断层面(万永革等，2008； Hayesetal.，2010； 盛书中等，2014； 高彬等，2016； 胡晓辉等，2019)。相关成果极大地推动了由余震空间分布确定断层参数的研究，但它们依赖于先验信息——须了解已有断裂的构造，或对地震空间分布的线性情况有所要求，因此这类方法难以处理线性趋势相对较差的地区。2)基于地震数据的空间丛集性，采用机器学习方法中的无监督聚类技术选取数据，该方法避免了对经验的依赖，且更加适应从海量地震数据中自动获取断层。如Ouillon等(2008)基于K-means聚类法提出的各向异性动态聚类方法(OADC)，该方法改进了K-means算法，使其不需要输入K值，并将其应用于美国兰德斯地震序列，获得了该地区的已知断层和隐伏断层。但该方法在选取数据时，默认将所有地震事件均分配给断层面，忽略了部分离散事件对断层参数拟合的影响。Skoumal等(2019)基于DBSCAN(Density Based Spatial Clustering of Application with Noise)算法提出了“断层识别”方法(FaultID)，并据此识别出美国俄克拉荷马州约2500个断层，其中多数断层为先前未被研究的断层，但该方法在选取数据时需经验性指定DBSCAN的2个全局参数。Kamer等(2020)提出“生长聚类”算法，选取数据并给出断层结构，由于该方法采用“自下而上”的模式，与其他方法相比对小规模、 复杂的断层结构的识别能力更强，但该方法仍需尝试不同的参数，以便获得最优结果。Brunsvik等(2021)首先采用谱聚类对地震数据进行初步挑选，其次采用DBSCAN选取Paganica断裂系统中各断层的数据，并最终给出L’Aquila地震序列相关断层的三维形态，但该方法在谱聚类以及DBSCAN聚类过程中仍然需要经验性地设置参数。因此，本研究基于以上方法，进一步提出改进的DBSCAN聚类算法，以自动识别断层，为快速、 自动反演断层的三维形态等提供新的思路和方法。

本研究改进了无监督聚类技术，实现了基于震源空间位置分布自动识别断层段并计算其参数。首先应用改进的DBSCAN聚类算法自动识别断层段，其次对识别出的断层段采用模拟退火全局搜索-高斯牛顿局部搜索结合法计算其断层参数，再对邻近的相似断层段进行合并，最终给出基于地震空间分布识别出的各断层段及其参数。为了验证该方法的可行性，我们首先将其应用于合成数据，其次将其应用于构造研究较为深入的唐山地区。

1 方法

本研究的目标是基于震源空间位置分布自动识别震源所刻画的断裂段，因此，提出改进的DBSCAN聚类算法以实现自动识别断层段。鉴于以下2方面考虑： 1)不同断层以及同一条断层不同段上的地震密集程度不同； 2)断层具有任意形状，且噪声将影响断层参数的拟合。我们选择对可以发现任意形状聚类、 能挖掘数据中密度变化且对噪声数据不敏感的考虑噪声的空间密度聚类算法(DBSCAN)进行改进(Skoumaletal.，2019； Brunsviketal.，2021)，以实现断层段的自动识别。

传统的DBSCAN算法由Ester等(1996)提出，该算法认为断层上的地震事件由“核心震源”和“边缘震源”组成，其余地震事件为噪声(“核心震源”为在给定半径eps的邻域内震源数量不小于minPts的震源； “边缘震源”为在eps邻域内震源数量小于minPts，但其自身处于核心震源的邻域内的震源)。在DBSCAN算法中，聚类是“密度相连”的集合，能够将足够高密度的数据联系在一起，并且在具有噪声的数据中能够发现任意形状的簇。前人经研究发现，传统的DBSCAN算法存在以下2方面缺陷： 1)聚类结果对全局参数eps和minPts比较敏感，如增大minPts会增加将断层上的地震事件误认为是噪声的概率，增大eps会增加将相邻的断层合并在一起的趋势及将非断层上的地震事件误认为是断层上的地震事件(Brunsviketal.，2021)； 2)单一的eps和minPts值无法同时识别活跃程度差异较大的断层段(侯雄文，2017a)。考虑到实际断层的复杂性，固定输入参数将导致在识别过程中丢失大量断层。因此，本研究针对以上缺陷对DBSCAN算法进行改进，使其能够在不同密度层次(侯雄文，2017a)的数据中自动识别断层段。

为了解决以上问题，本文在付泽强等(2018)和李文杰等(2019)研究的基础上，进一步改进DBSCAN算法。李文杰等(2019)提出利用K-平均最近邻算法(K-Average Nearest Neighbor，K-ANN)和数学期望法生成eps和minPts阈值参数的候选集合，再基于密度层次稳定的情况选取最优参数(侯雄文，2017b)。K-平均最近邻算法是K近邻法(K-Nearest Neighbor，KNN)和平均最近邻法(Guyonetal.，2002； Changetal.，2011)的延伸，该算法的基本思想是通过计算地震目录中每个地震事件与其第K个最近邻事件之间的K-最近邻距离，并对所有数据点对的K-最近邻距离求平均值，得到数据集的K-平均最近邻距离。之后，对所有K值进行计算，得到K-平均最近邻距离向量，即eps参数候选集合。

对于给定的eps参数候选集合，依次求出每个eps参数对应邻域的地震事件数量，并计算所有对象的eps邻域数量的数学期望值，作为minPts参数候选集合。计算地震目录D的minPts参数候选集合的具体公式为

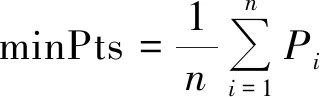
(1)

其中，Pi为第i个对象的eps邻域对象数量，n为地震目录D中的对象总数。

考虑到获得可靠的断层参数所需的地震数量不能过少，本研究采用来自于数据自身特征的簇内最小事件数(M)作为断层段识别的终止条件，并将其称为有效事件数阈值(M＿effect)，下面简述该值的确定过程。我们用矩形框对地震数据中呈条带状且较为稀疏的区域进行框选，统计框内发生的地震事件数M。 考虑到M值的确定存在较大的主观因素，该数值精度较低，因此，本研究中将M向下取整到十位数得到M＿effect。若算法所识别断层内的地震事件数不小于M＿effect，则称其为有效断层。

为了尽可能地识别断层，本研究采用由高到低的逐层密度聚类法。断层上的地震密度差异很大，使得在断层识别时，地震稀疏段相对于地震密集段更容易被误识为“噪声”。因此，在本研究中，为了解决地震事件空间密度差异带来的问题并尽可能地识别出研究区的断层，我们从高密度层次到低密度层次对地震目录进行多次不同密度层次的聚类(付泽强等，2018)。在对下一密度层次断层聚类前，将上一密度层次识别的有效断层数据删除，保证高密度断层的数据不影响低密度断层的识别(Skoumaletal.，2019)。下面介绍各密度层次最优参数eps和minPts的确定方法。从小到大选用不同K值(K=1，2，…，n)所对应的eps和minPts，对地震目录进行聚类，分别得到在不同K值下生成的有效断层数目。在上述过程中，当有效断层数目连续3次出现相同值时，定义其密度层次达到稳定，记该有效断层数目为最优数目N。 直到某K值所对应的有效断层数目不再为N，此时密度层次发生改变。将有效断层数目N对应的最大K值视为最优K值，该K值对应的eps和minPts为当前密度层次的最优参数(李文杰等，2019)。

基于地震丛集性地发生在断层面上的研究，万永革等(2008)提出用模拟退火全局搜索-高斯牛顿局部搜索相结合的方法拟合断层面参数。该方法将全局搜索和局部搜索相结合搜索一个平面，使得该平面到丛集性小地震的距离最小。该方法可以有效地避免对初始解的依赖，从而获得全局最优解。本研究将基于上述断层段自动识别结果，应用万永革等(2008)的方法计算各段断层面的参数及其误差。

考虑到同一断层不同段的活跃程度不同，即密度层次不同，在自动识别断层段的过程中，同一断层可能被识别为2段。因此，在本研究中，将2个断层面参数相近且紧邻的断层段合成为一段，并计算最终的断层面参数。

上文简述了本研究提出的基于改进的DBSCAN聚类算法自动识别断层的方法，其具体实现步骤如下：

步骤1： 根据研究数据确定M＿effect。

步骤2： 计算地震目录D的距离矩阵Dn×n。本研究采用半正矢公式(Markouetal.，2010)计算距离，具体公式为

(2)

其中，R为地球半径；φ1、φ2表示2个地震事件的经度；λ1、λ2表示2个地震事件的纬度；d为半正矢距离。

Dn×n={d(i，j)|1≤i≤n，1≤j≤n}

(3)

其中，Dn×n为n×n的实对称矩阵；n为地震目录D中地震事件数；d(i，j)为地震目录D中第i和j个事件间的半正矢距离。

步骤3： 对距离矩阵Dn×n的每行元素进行升序排序，则第1列元素所组成的距离向量D0表示对象到自身的距离全为0。第K列元素构成所有地震事件的K-最近邻距离向量DK。

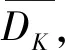
(4)

步骤5： 根据式(1)计算Deps对应的minPts，得到候选minPts集合DminPts。

步骤6： 依次用不同K值(K=1，2，…，n)所对应的参数对地震目录进行聚类，得到不同K值聚类的有效断层数目。当连续3次K值所对应的有效断层数目为N时，称N为最优数目。

步骤7： 继续执行步骤6，直至有效断层数目不再为N，则有效断层数目为N时的最大K值为最优K值。最优K值对应的eps和minPts则为最优参数，基于该最优参数进行断层段识别。

步骤8： 对识别出的有效断层数据进行断层面参数计算，并将其从地震目录D中删除，对剩余地震数据执行步骤2—8，重复上述步骤直至其识别断层内的地震事件数均小于M＿effect时，断层识别终止。

步骤9： 对相邻且参数相近的断层段进行合并，计算断层参数。

2 理论测试

2.1 生成合成数据集

为了检验本研究提出的方法，我们生成密集分布于断层面上的地震事件和遍布整个空间的随机地震事件(即噪声)，由地震事件和噪声事件组成合成数据集。首先，我们在空间{0≤x≤1，0≤y≤1，-10≤z≤0}(x、y和z分别表示经度(°)、 纬度(°)和深度(km))上生成分布于3个断层面上的地震数据，且假定震源点围绕3个子断层面服从正态分布，其分布区间为(-0.02°，0.02°)。断层面方程分别为断层1：x=0.5，断层2：y=0.3和断层3：y=0.7。断层1、 断层2和断层3上的地震事件数分别为800、 1000和1200个(图1a)。其次，在研究区域内添加随机地震事件，添加的地震数分别为总地震事件数的5%、 10%和20%(图1b—d)。

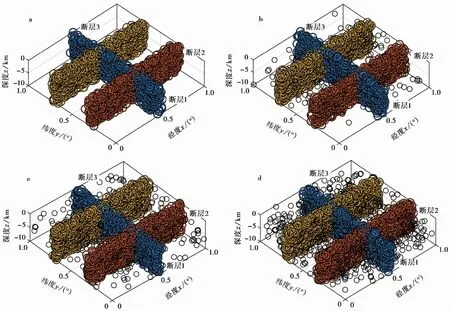
图 1 a 人工合成地震数据； b—d 分别添加总地震事件5%、 10%和20%随机地震后的地震空间分布图Fig. 1 The spatial distribution of synthetic seismic data(a) and adding random earthquakes which account for 5%，10% and 20% of total seismic events(b—d)，respectively.黑色圆圈表示随机地震(即噪声)，其余为断层上的地震事件

2.2 自动识别断层面方法的测试

下面我们使用合成数据对上文所述的断层面识别方法进行测试，测试过程以添加5%噪声事件的合成数据为例。首先，选择其数据中呈条带状且较为稀疏的矩形区域计算M＿effect，得到的M＿effect为80(图4a)。其次，按照上文所述步骤和方法进行第1密度层次聚类。由生成聚类K与eps和minPts的关系图(图2a，b)以及K与有效断层数目的关系(图3a)确定最优K值为12，其对应的最优聚类参数eps和minPts为2.23和18(图2a，b)。基于以上最优参数进行聚类，获得6个有效断层和8个无效断层。将已识别的有效断层数据删除，对剩余数据重复上述步骤，进行第2密度层次聚类。由图2c、 2d和3b可见，聚类最优K值为19，其所对应的最优聚类参数eps和minPts为6.39和45。基于以上最优参数进行聚类，获得4个有效断层和1个无效断层。再将已识别的有效断层数据删除，对剩余数据进行第3密度层次聚类，本次聚类的最优K值为26，所识别簇内事件数均小于M＿effect，停止聚类。

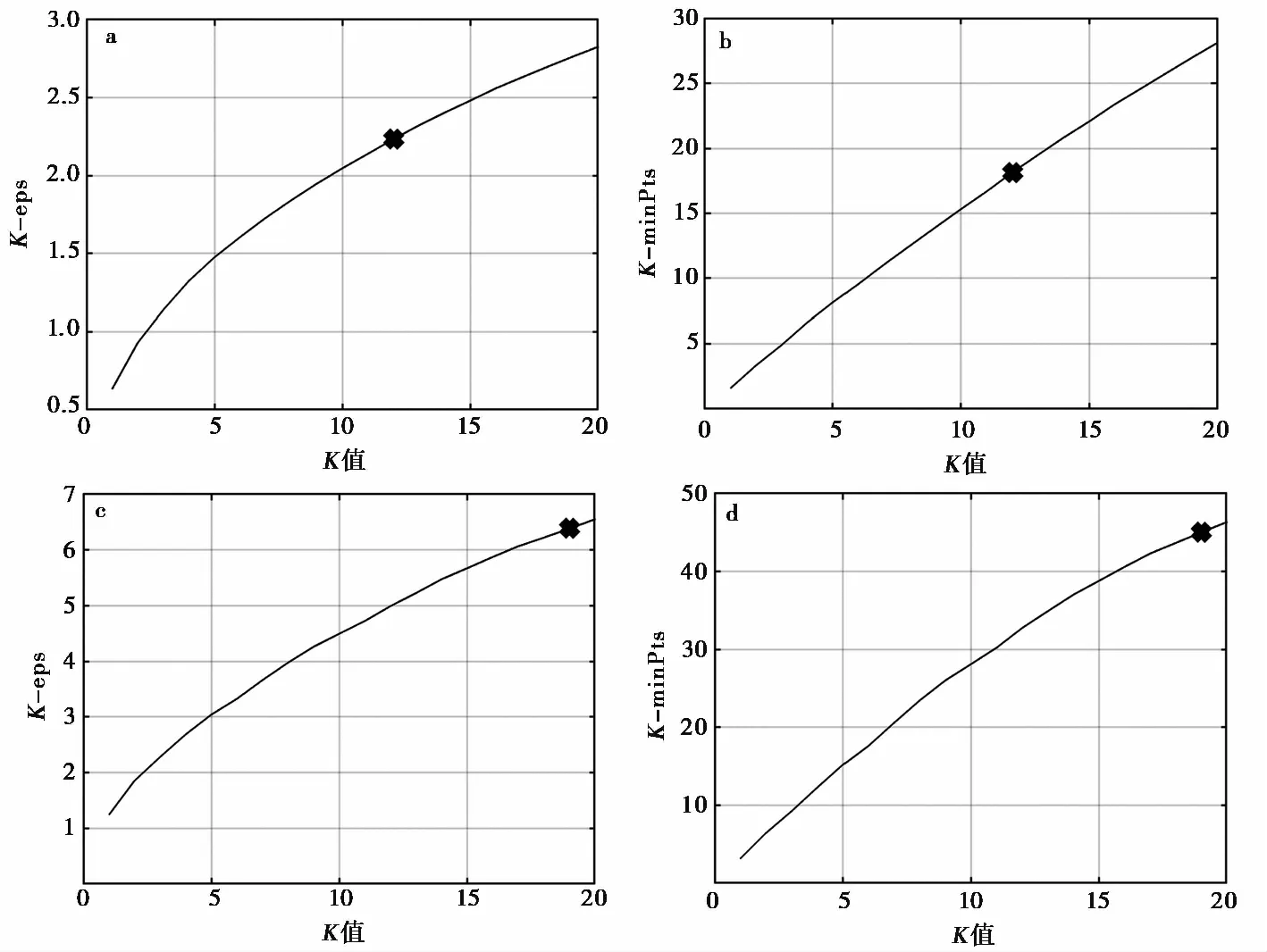
图 2 添加5%噪声的合成断层数据第1次聚类(a、 b)和第2次聚类(c、 d)的K-eps、 K-minPts关系图Fig. 2 K-eps，K-minPts diagrams of first clustering(a，b) and second clustering(c，d) for synthetic data with 5% noise.标记处为最优参数

对合成数据集进行了3个密度层次聚类，自动识别出19个聚类，其中有效聚类为10个(图4a)。图4a 中4和5断层段，7、 8和9断层段的走向相近且相邻，因此，将其分别合并为同一断层段。1、 3、 6和10断层段走向相近但不相邻，考虑到识别共轭断层处时往往将同一断层划分为多段，因此将其合并为同一断层段。最终在研究区获得3个断层面(图4b)。重复上述方法分别处理噪声水平为10%和20%的合成数据，最终识别出的断层面情况见图4c、 4d。

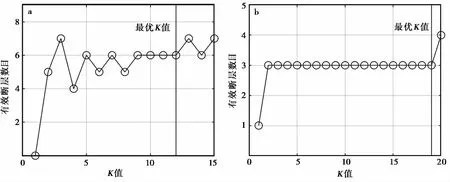
图 3 添加5%噪声的合成数据第1次聚类(a)和第2次聚类(b)的K值与有效断层数目关系图Fig. 3 K-number of effective faults diagram of first clustering(a) and second clustering(b) for synthetic data with 5% noise.

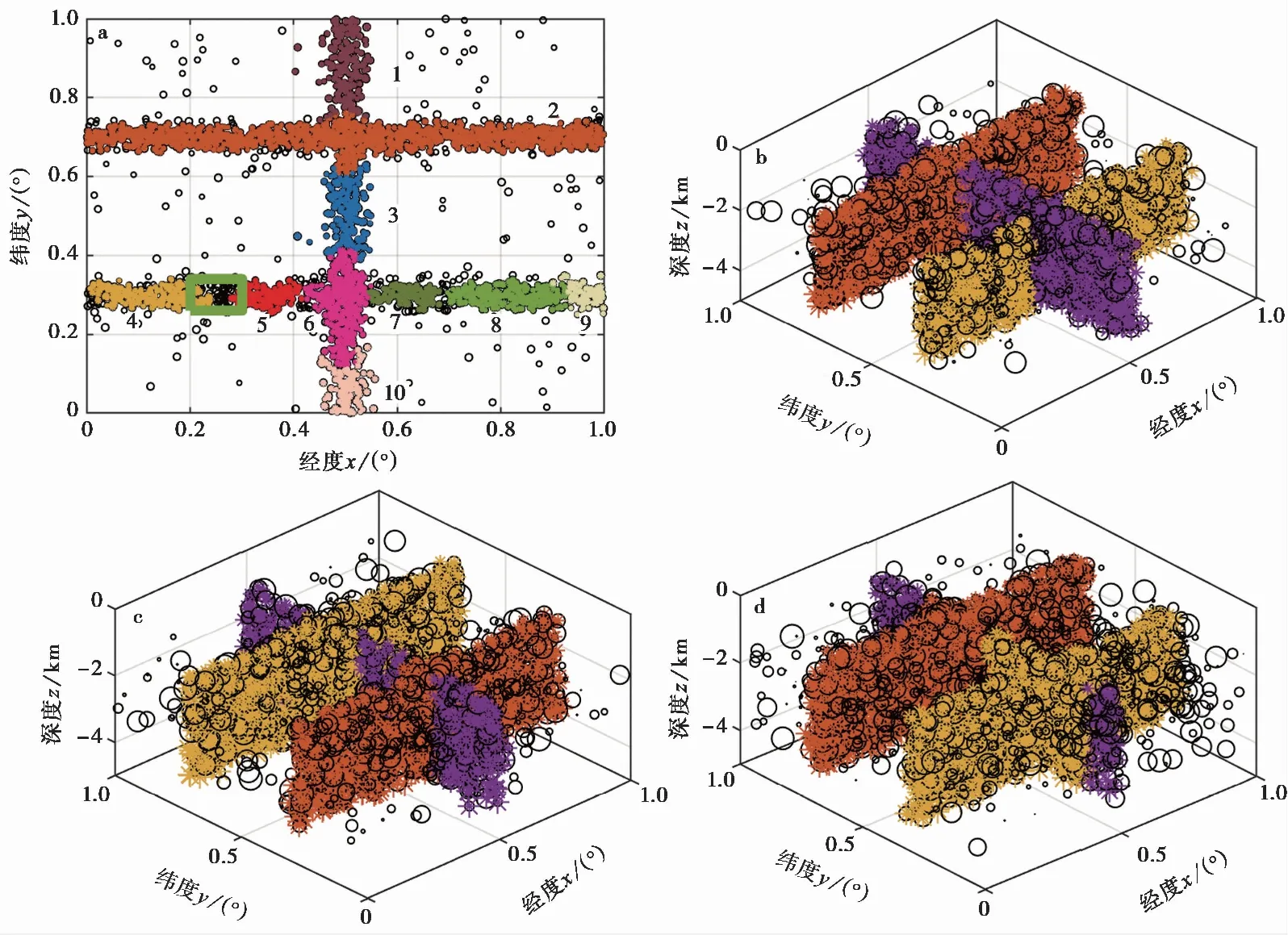
图 4 添加噪声数据自动识别断层面的结果Fig. 4 Automatic fault plane recognition results for synthetic data.a 添加5%噪声的合成数据未合并的识别结果，矩形框为最小事件数阈值选取区域； b 添加5%噪声的合成数据断层面合并后的识别结果； c 添加10%噪声的合成数据断层面合并后的识别结果； d 添加20%噪声的合成数据断层面合并后的识别结果； 用不同颜色标示识别出的断层段

2.3 测试结果分析

基于改进的DBSCAN算法，对添加不同噪声水平的合成数据进行识别，得到的断层结果如图 4 所示。由图 4 可见，本文的算法可以较好地识别出理论断层，随着噪声的增加，断层面识别的效果稍有降低。

由于假定的断层面是共轭断层，断层上的地震分布存在交集，而本研究提出的算法将交集部分数据归于某条断层上，会出现将共轭断层中的一条断层识别为不连续的断层段的现象(图 4)，这种不连续总体上对断层认识的影响较小。

3 在唐山地区的应用

3.1 数据

改进的DBSCAN算法理论测试结果较好。下面我们将用地震活跃且研究程度较高的唐山地区的地震数据对其做进一步测试。研究区的范围为(39°～40°N，117.2°～119.2°E)，数据为经双差定位后的4256次地震事件，时间范围为2000年1月1日—2011年4月3日，震源深度分布在0～20km，震级主要为ML<2.7(图 5)。地震分布明显呈条带状，有利于本文断层识别方法的应用。

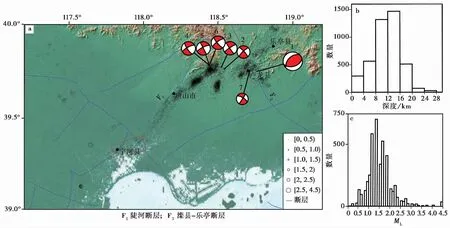
图 5 唐山地震序列的震中(a)、 深度(b)和震级(c)分布图Fig. 5 Distribution of epicenter(a)，depth(b)and magnitude(c) of the Tangshan earthquake sequence，China.矩形框为最小事件数阈值的选取区域

3.2 断层自动识别结果

重复与理论测试部分相同的数据处理步骤，自动识别出唐山地区的断层段。基于图 5 框内的97个地震事件数据，确定M＿effect为90。其次，对数据进行不同密度层次聚类，基于上述终止原则进行了4次聚类，其最优K值分别为10、 4、 5和14(图6a—d)； 最优eps参数分别为1.6、 1.9、 2.7和5.5； 最优minPts参数分别为59、 15、 14和27。最终自动识别出不同密度层次的37个聚类(图7a—d)，满足条件的有效断层有11个。

通过对11段断层面参数进行对比分析及合并，最终获得8个断层(图 8，表1)： 第1段和第4段(图7a)、 第4段和第11段(图7b)的走向差异分别为2.7°和2.0°，倾角差异分别为2.0°和2.4°，将上述3个断层段合并为巍山-丰南断裂段断层(f1)； 第3段(图7a)和第6段(图7a)的走向差异为9.6°，倾角差异为2.0°，将其合并为滦县断裂北段(f3)。我们根据8个断裂段附近的断层和城市确定其名字，具体见图7e。

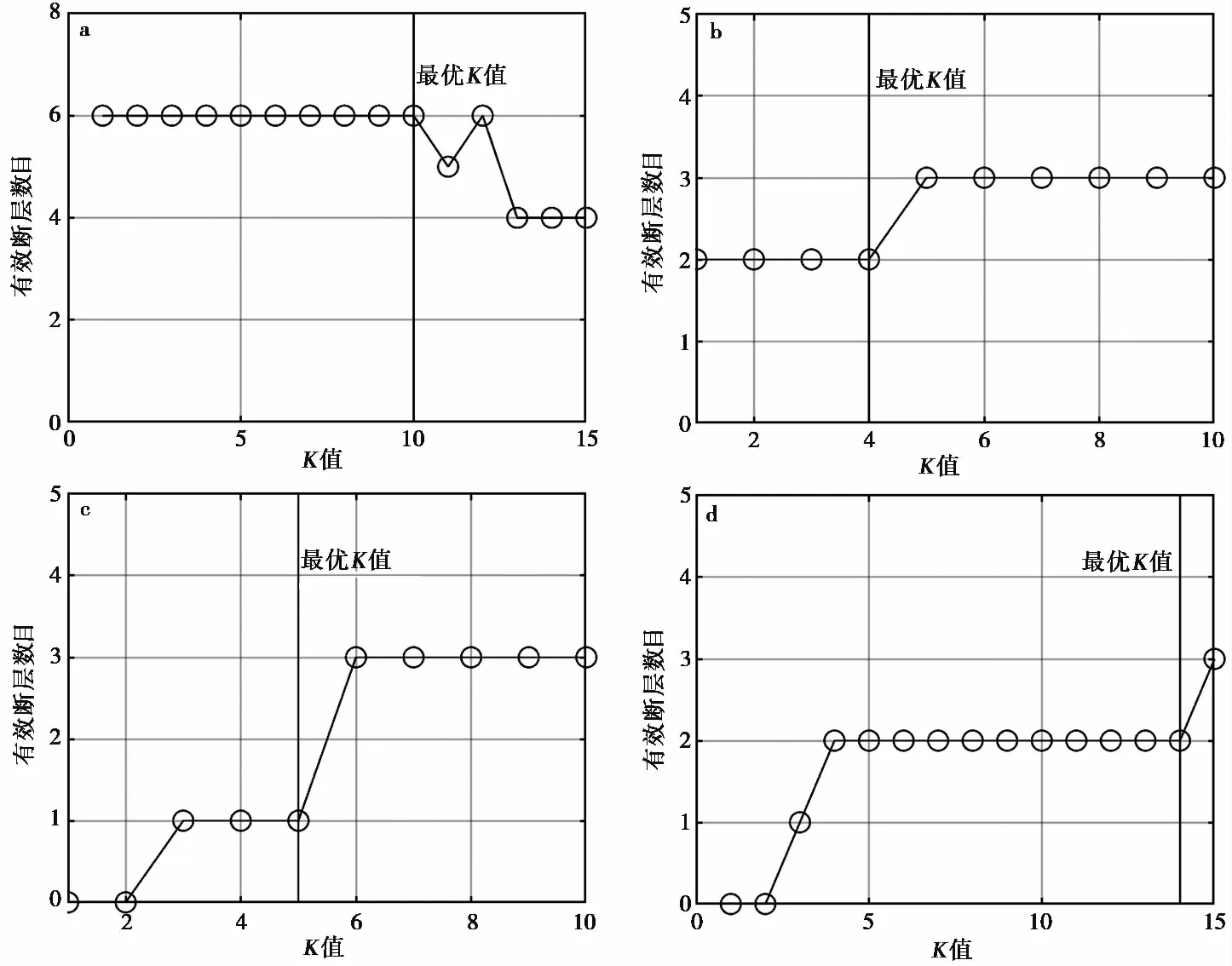
图 6 唐山地区4层密度聚类的K值与有效断层数目的关系图(a—d)Fig. 6 Relationship between K value of four-level density clustering and the number of effective faults in Tangshan area(a—d).

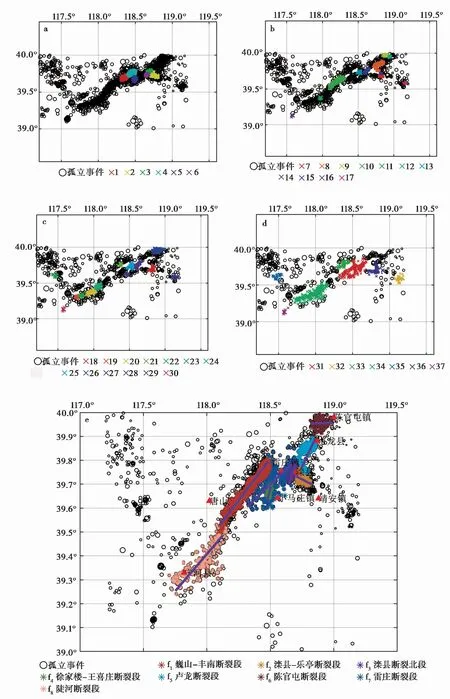
图 7 唐山地区第1、 2、 3、 4次聚类结果图(a—d)和最终断层识别结果图(e)Fig. 7 Graph of the first，second，third and fourth clustering results(a—d) and final fault identification results(e)in Tangshan area.

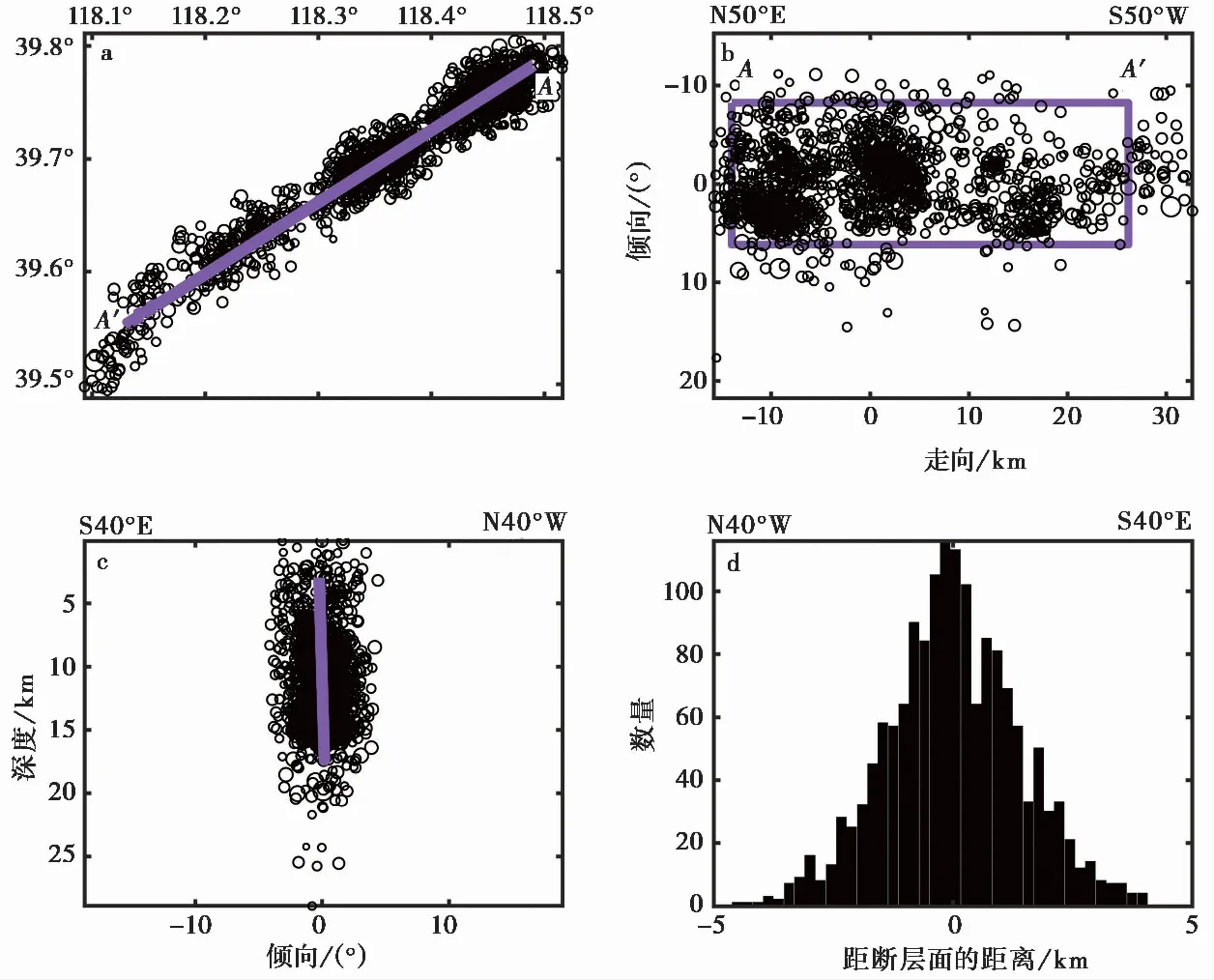
图 8 巍山-丰南断裂段(f1)的小地震拟合结果Fig. 8 The fitting result by using small earthquakes of Weishan-Fengnan Fault(f1).a 小地震的水平面投影； b 小地震的断层面投影； c 小地震垂直于断层面的横断面投影； d 小地震与断层面的距离

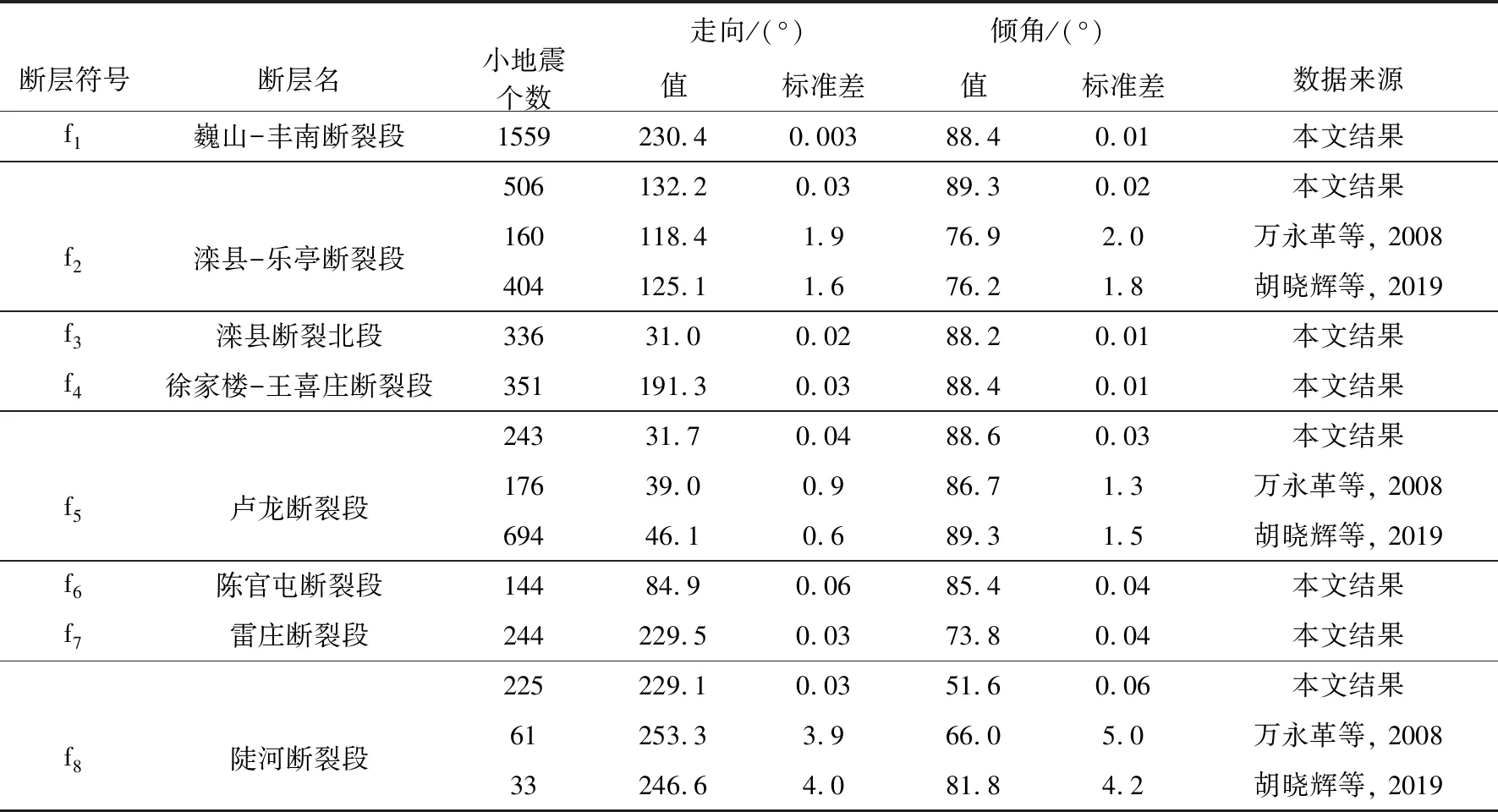
表 1 利用本文方法求得的唐山地区各段断层面的走向、 倾角和标准差Table1 Fault plane parameters of Tangshan region obtained by using the automatic fault identification method

3.3 断层识别结果分析

为了分析本研究结果的可靠性，我们将研究结果与唐山断裂带的实际活动断裂(杨雅琼等，2018)、 基于震源机制解的断裂分段结果(杨雅琼等，2016)和经验性分段结果(万永革等，2008； 胡晓辉等，2019)进行对比分析。万永革等(2008)经验地划分出陡河断裂段、 巍山-丰南断裂南段、 巍山-丰南断裂北段、 滦县-乐亭断裂段和卢龙断裂段； 杨雅琼等(2016)采用震源机制解划分出巍山-丰南断裂南段、 巍山-丰南断裂北段、 滦县-乐亭断裂段和卢龙断裂段。本文方法的识别结果同样包括陡河断裂段、 巍山-丰南断裂段、 滦县-乐亭断裂段和卢龙断裂段，但将巍山-丰南断裂南段与巍山-丰南断裂北段合为一段。研究者在唐山断裂带分段方面存在一定争议： 万永革等(2008)将其经验性地分为3段； 杨雅琼等(2016)基于震源机制解将其划分为2段，分界点位于唐山市附近。 本研究将唐山断裂带划分为2段，且分界点位于唐山市西南方向(图7e)。可见，本文结果与前人的研究结果存在异同，本研究结果与唐山断裂的实际活动更加一致(图 10)。

本文研究结果中的陡河断裂段(f8)、 卢龙断裂段(f5)和滦县-乐亭断裂段(f2)与万永革等(2008)、 胡晓辉等(2019)所给出的结果差异见图 9。总体上看，本文结果与万永革等(2008)结果的走向差异大于胡晓辉等(2019)的结果，反映了地震定位误差对断层面参数拟合的影响。胡晓辉等(2019)搜集了18组由不同学者或机构给出的同一地震断层面的参数差异，获得的走向和倾角差异范围分别为2°～34°和2°～28°。以此差异作为参考，除陡河断裂段(f8)与胡晓辉等(2019)的倾角差异外，本文得到的走向和倾角与前人研究结果的差异值均在统计范围内(图 9)。由于胡晓辉等(2019)基于中国地震台网统一地震目录拟合参数，其数据误差较大(黄文辉等，2016)，且本文陡河断裂段的倾角与万永革等(2008)的差异仍在统计范围内，故可认为本文研究所得结果是可靠的。滦县-乐亭断裂段(f2)的断层面参数相比杜晨晓等(2010)根据三维有限差分断层瞬态破裂动力学模型反演得到的走向偏大12.2°、 倾角偏大9.3°。本研究的结果表明，唐山地区除陡河断裂段(f8)和雷庄断裂段(f7)外均为近直立断层(表1)，这与前人的研究结果相同(李钦祖等，1980； 张之立等，1980； 万永革等，2008； 刘亢等，2015； 胡晓辉等，2019)。

图 9 本文结果与前人研究结果走向(a)和倾角(b)的差异值Fig. 9 Difference of fault strike(a)and dip(b)between the results of this paper and those of previous studies.线段为胡晓辉等(2019)总结的断层参数差异范围

本研究所得结果除与上述研究一致外，在其余4条断层中，有2条断层的参数与地质资料给出的断层参数相符，1条断层参数与其上发生的震源机制解参数相近。刘亢等(2015)和杨雅琼等(2016)的研究结果表明，在古冶小地震密集区的东侧存在一条新生地震带，这与徐家楼-王喜庄断层(f4)相吻合。刘亢等(2015)得到其为近NNE向的近直立断层，与本研究的结果基本一致(表1)。本文新识别的滦县断裂北段(f3)与唐山地质图中NE向的卢龙断层(图 10)较为一致； 本文新识别的雷庄断裂段参数与其上发生的震源机制解参数一致； 本文新识别的陈官屯断裂段(f6)仍有待进一步证实。

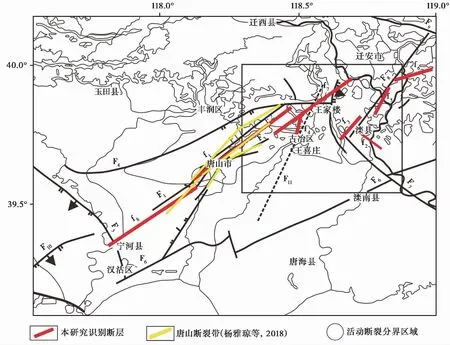
图 10 唐山地区的主要断层分布图(刘亢等，2015)Fig. 10 Distribution of major faults in Tangshan area(after LIU Kang et al.，2015).F1陡河断层； F2巍山-丰南断层； F3古冶-南湖断层； F4丰台-野鸡坨断层； F5蓟运河断层； F6宁河-昌黎断层； F7滦县-乐亭断层； F8卢龙断层； F9建昌营断层； F10沧东断层； F11徐家楼-王喜庄断层

断层上地震的震源机制解，其节面之一的参数和断层参数相似，因此常被用于验证所识别断层参数的可靠性(Ouillonetal.，2008； Wangetal.，2013； 盛书中，2015； 盛书中等，2015； Skoumaletal.，2019)。为了分析本研究所得结果的可靠性，我们将其与搜集到的断层上的震源机制解(表2)进行对比分析。本文得到的卢龙断裂段的走向小于震源机制解的走向(40.3°)，从图7e 可见，由于该断层段聚类的震中分布呈分段线性，而本研究中将其视为一段拟合，由此导致走向差异过大。本文所得雷庄断裂段的走向与2次雷庄断裂段上的震源机制解走向差异分别为2.5°和6.5°，倾角差异分别为6.2°和7.2°，证实了本文新识别的雷庄断裂段的可靠性。本文识别的巍山-丰南断裂段于2020年7月12日发生唐山古冶区5.1级地震，本文所得断裂段的走向相比3所机构测定的震源机制解(表2)走向分别偏小10.6°、 12.6°和3.6°； 倾角分别偏大15.4°、 13.4°和15.4°。本文识别的滦县-乐亭断裂段于2021年4月16日发生唐山滦州市 4.3级地震，本文所得断裂段的走向相比震源机制解(表2)走向偏大10.2°、 倾角偏大14.3°。考虑到线性拟合可能会与实际断层形态不符(曾宪伟等，2019)，因此，本文的研究结果与断层上震源机制解存在较小差异是合理的。综上所述，与现有震源机制资料相比(表2)，除卢龙断裂段因呈分段线性导致较大误差外，其他断层参数与断层上震源机制解的差异均在合理范围内。

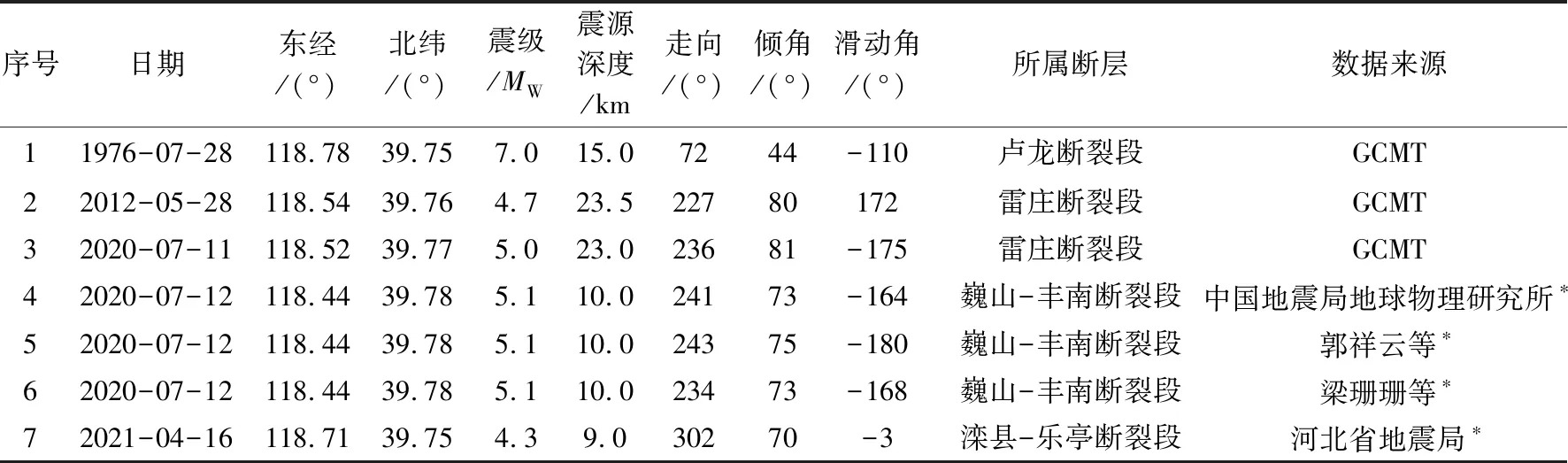
表 2 震源机制解目录Table2 Catalog of focal mechanism

总体来看，除卢龙断裂段外，本文所识别断层的倾角均大于震源机制解倾角。我们认为造成倾角偏大的主要原因是双差精定位后地震分布高度集中，带状分布更明显，双差定位后震中宽度分布的压缩大于其在深度上的压缩，且在断层参数拟合的过程中仅采用内部90%的小地震所在区域确定断层面的4个顶点位置(万永革等，2008)，最终造成本研究拟合倾角均偏大的结果(图8b)。

4 结论与讨论

本研究改进了DBSCAN算法，实现了由震源位置空间分布数据自动识别断裂段，并将该方法应用于合成数据和唐山地区。合成数据和唐山地区断层的成功识别表明： 1)本研究所提出的改进的DBSCAN算法可以实现断层段的自动识别； 2)基于精定位数据，在唐山地区自动识别出8条断层段，本研究所得结果与经验分段(万永革等，2008； 胡晓辉等，2019)和震源机制解分段(杨雅琼等，2016)较为一致，表明本研究提出方法的合理性和有效性。

本研究所述方法在自动识别断层过程中，采用了从高密度层次到低密度层次的多密度层次聚类，因此，本研究方法是从高密度向低密度的有序递进，与其他方法相比其优点在于提高了对于低密度地震数据中断层的识别能力。本研究方法相比前人的断层识别方法(Scitovski，2017； Shangetal.，2018； Skoumaletal.，2019； Kameretal.，2020； Brunsviketal.，2021)部分地解决了经验性选择参数问题，但仍存在以下缺陷： 1)有效事件数阈值的确定具有主观性。在后续研究中，我们将考虑如何避免该主观因素的影响。2)将实际断层面近似为平面，难以反映实际断层的三维复杂形态，如汶川地震断层的铲状构造(张培震等，2012)、 俯冲带弧状构造(张泽明等，2021)等复杂情况。为了提高自动识别断层的精度，在后续的研究中，我们将考虑实际断层的三维形态，对空间进行网格化，获取每个网格单元内的断层元，再以空间插值的方式连接所有断层元，给出符合实际的三维断层。3)本研究中忽略了深度因素，仅使用震中距离进行聚类。唐山地区断裂以近直立的走滑型断裂为主，且噪声水平相对较低，本研究所得结果较为合理和可靠，在后续研究中，将使用震源距离进行聚类，以适应复杂断裂构造的识别。

基于上述分析可见，本研究改进的DBSCAN算法可以较好地实现断层段的自动识别，但仍存在以上亟需改进的问题。在后续研究中，我们将继续对断层段自动识别方法进行改进，提高其自动识别断层能力，为活动断层的应变分析、 地震地质灾害评估和断层滑动趋势等相关研究提供更加准确的断层资料。

致谢防灾科技学院万永革研究员为本文提供了模拟退火全局搜索-高斯牛顿局部搜索结合法的程序； 东华理工大学刘茜茜硕士、 防灾科技学院许鑫硕士、 李枭硕士和冯淦硕士对本文绘图提供了帮助与指导； 审稿专家对本文提出了宝贵意见； 部分图件采用GMT(Wesseletal.，1998)软件绘制。在此一并表示感谢！