基于混合空谱全变差和双域低秩约束的高光谱图像去噪

张鹏丹，宁纪锋

（西北农林科技大学 信息工程学院，陕西 杨凌 712100）

0 引言

高光谱成像是利用成像光谱仪在同一场景获取多个光谱波段图像的一种技术。它具有广泛的应用，涉及环境、农业、军事和地理等诸多领域［1-4］。然而，由于受传感器灵敏度、光子效应、光照条件和校准误差等因素的限制，高光谱图像（Hyperspectral Image，HSI）在实际获取过程中总是被噪声严重污染。因此，作为后续研究任务的前提，HSI 去噪并获取清晰的图像是一个亟待解决的问题。

早期的图像去噪方法将每个波段视为灰度图像，然后将灰度图像去噪方法直接逐波段的对HSI 数据进行去噪处理。MANJÓN J V 等［5］在稀疏表示理论基础上，提出基于K-SVD 的去噪算法；DABOV K 等［6］提出了一种基于变换域增强稀疏表示的图像去噪方法。虽然这些方法起到了一定的去噪作用，但是由于逐波段去噪并没有充分利用HSI 的空间和光谱相关性导致去噪效果并不令人满意。LETEXIER D 和LIU Xuefeng［7-8］将HSI 视为三维张量立方体，联合考虑空间几何结构和光谱的连续性，提出了多维维纳滤波去噪模型。后续研究中，这类模型因为操作简单而被广泛应用，例如：AEO H 等［9］针对HSI 数据特性提出了多变量多分辨率主成分分析的信号滤波去噪模型；BOLLENBECK F 等［10］在双边滤波的基础上提出了联合双边滤波去噪模型，加强了图像的特征和细节保存。虽然这些方法在去除特定噪声时效果明显，但并不擅长混合噪声的去除。

清晰的HSI 具有稀疏性和低秩性两个重要特征。基于这两个特征，衍生出了许多优秀的去噪模型。关于低秩先验，核范数最小化［11］、CANDECOMP/PARAFAC（CP）分解［12］、Tucker 分解［13］和张量奇异值分解（t-SVD）［14］等方法常常被用于刻画HSI 的低秩特征。结合上述方法，学者们提出了大量基于低秩先验信息的去噪模型，并且取得了不错的效果。ZHENG Yubang 等［15］提出了一种新的基于t-SVD 的张量纤维秩，并建立了一种用于去除HSI 混合噪声的纤维秩最小化模型。FAN Haiyan 等［16］引入了新的t-SVD 和张量核范数（Tensor Nuclear Norm，TNN ）来去除混合噪声。YUAN Yuli 等［37］将非凸低秩约束与块稀疏相结合提出了WBS-MCP 模型，有效去除了条带噪声。LIU Sheng 等［38］提出了频率加权张量核范数的概念，并给出了频率域权重的自适应确定方法，提出的模型能够有效保留图像纹理细节。WANG Zhongmei 等［39］利用非局部自相似性和光谱相关性提出新的去噪模型并通过张量分解进行求解，在去除噪声的同时能够保持图像边缘。WANG Minghua 等［17］结合了低秩张量Tucker 分解和0梯度正则化来去除HSI 混合噪声。WU Xiaoce等［18］将稀疏与Tucker 秩结合起来用于更好地获取空间方向和光谱方向的相关性。但是TNN 在逼近张量秩函数的精度上有一定的局限性，其计算也比较复杂。Tucker 秩因为计算方便和不破坏高阶结构的优势被广泛应用。

在传统图像处理领域中，全变差（Total Variation，TV）用于表示自然图像的稀疏特征，能够有效探索图像空间域的平滑信息。由于TV 在图像去噪等病态反问题中表现出良好的性能，因此被推广到光谱图像去噪问题中并衍生出多种变形。经典的各向异性光谱-空间全变差（Anisotropic Spectral-Spatial Total Variation，ASSTV）［19］分别在空间维度和光谱维度做差分，很好地探索了光谱和空间维上的平滑性。HE Wei 等提出了全变差正则化低秩矩阵分解模型（TV-Regularized Low-Rank Matrix Factorization，LRTV）［20］，大大提高了HSI 去噪的精度，为今后HSI 的恢复问题提供了一个很好的思路。ZENG Haijin 等［21］提出了一种三维空间光谱总变异（3-D Spatial-spectral Total Variation，3-DSSTV）的正则化方法，能够同时去除多种噪声。YUAN Qiangqiang 等［22］提出了一种采用光谱-空间自适应全变差（Spectral-spatial Adaptive Total Variation，SSATV）模型的HSI 去噪算法，在降噪过程中既考虑了光谱噪声的差异，也考虑了空间信息的差异。TAKEYAMA S 等［23］提出了混合空间光谱全变差（Hybrid Spatio-spectral Total Variation，HSSTV）方法，该方法在去除噪声和伪影方面取得了很好的效果。然而，基于TV 的模型很容易造成过度平滑。因此，在构造新模型时需要考虑抑制过度平滑的因素。LRTDTV 模型［24］在经典的ASSTV 正则化基础上加上了张量低秩，大大提高了去噪精度。LLRSSTV 模型［25］对分割出来的小块采用低秩约束然后进行重建，能够有效去除相邻像素间结构相似的噪声。LLR-L1-2SSTV 模型［40］利用L1-2TV 提出稀疏表达能力更强的全变差正则化项，同时在局部使用核范数最小化来加强低秩约束，在去除混合噪声的同时能够有效抑制与结构相关的噪声。LRTDGS 模型［26］提出了组稀疏的概念，结合ASSTV 和Tucker 分解有效地提高了图像去噪的精度。

一直以来，从噪声图像中恢复有意义的高质量HSI 受到人们长期关注，不断更新的技术手段要求去噪后的HSI 能够保留更多的原始信息。如何构建符合需求的去噪模型以及高效率的求解模型成为人们亟待解决的难题。从上述分析可以看出HSSTV 在光谱和空间维度上表现出色，尤其是对空间和光谱维度进行了二阶混合梯度，能够探索更高阶梯度蕴含的信息。通过进一步研究，发现HSSTV 梯度域具有组稀疏和低秩的特征。基于此，本文对HSSTV 采用了加权的范数，非常契合地表现了高阶梯度下的组稀疏特征，同时利用经典的核范数最小化来表现梯度域的低秩特征。另外，与Tucker 分解保证的原域低秩相结合，提出了适用于HSI 去噪的混合空谱全变差低秩张量分解模型（Hybrid Spatio-spectral Total Variation Regularized Low-rank Tensor Decomposition，LRHSSTV）。本文采用交替方向乘子算法（Alternating Direction Method of Multipliers，ADMM）迭代求解对应模型，获得干净的HSI。结果表明本文模型不但能够有效去除混合噪声，对结构和细节的保存也相对完整。

1 模型理论基础

1.1 HSI 去噪问题描述

一般情况下，观测到的HSI 会受到混合噪声的影响，通常包括高斯噪声、条纹噪声、死线和脉冲噪声等。假设HSI 是一个三阶张量X∈Rm×n×p，空间维度大小为m×n，波段数为p。获取到的HSI 可以表示为

式中，Y，S，N∈Rm×n×p，Y表示观测到的HSI；S代表稀疏噪声；N代表高斯白噪声。

HSI 去噪的目的是将含噪HSI 中的混合噪声分离出来，最终得到清晰的HSI，这是一个严重的不适定逆问题。在正则化理论框架内，上述逆问题求解问题可以表示为

式中，J(X，S，N)为保真项；R(X)表示清晰HSI 的先验信息；β是用于平衡两项的非负正则化参数。如果选择合适的HSI 先验信息及其精确的正则表示形式，那么去噪框架式（2）就可以求解出高质量的去噪结果。

1.2 HSSTV

HSSTV［23］不仅能表示HSI 空间1 阶梯度的稀疏性，还能探索空间和光谱维度的高阶混合梯度稀疏结构。HSSTV 的数学表达式为

与ASSTV［9］在竖直、水平和光谱三个维度独立探索1 阶梯度稀疏性相比，HSSTV 更着重对空间和光谱混合梯度稀疏性的研究，而且它将一阶梯度与二阶梯度相结合，有效抑制了过度平滑的现象。图1 上半部分展示了HSI 数据做完梯度之后的稀疏特性。从四张直方图中可以看出做完梯度之后的数据大部分为0，其余数据也十分接近于0，具有强稀疏特性。HSSTV 可以在空间和光谱域中提供更近似的稀疏先验表示，在HSI 图像去噪领域更有优势。

图1 LRHSSTV 去噪模型示意Fig.1 Schematic of LRHSSTV denoising model

2 LRHSSTV 模型

2.1 LRHSSTV 正则项和梯度域低秩

由于HSI 数据做完梯度之后具有组稀疏的特性，即沿着光谱维度每个tube 要么都是非零，要么都为零。为了强调这种特征，采用加权的范数来对梯度域组稀疏先验进行正则化，即，沿光谱维度的数据求取范数，然后对得到的矩阵求取范数，使其能更好进行组稀疏表示。与常用的范数相比，能够探索高阶梯度的内在结构信息，更能有效刻画这种稀疏特征。梯度域的范数可表示为

式中，D'=(DvDb，DhDb，Dv，Dh)，DvDb，DhDb分别表示竖直-光谱梯度算子和水平-光谱梯度算子，Dv和Dh表示空间梯度算子；W=(W1，W2，W3，W4)，0 ＜Wi＜1，(i=1，2，3，4)；‖ · ‖2，1表示将梯度张量每个像素处的梯度光谱曲线求范数，然后对所有范数求和。

根据经验可知清晰的HSI 数据具有低秩性的特征，如图1 中三幅奇异值曲线图所示，只有小部分的奇异值大于0，奇异值曲线呈明显的衰减趋势。此外，与HSI 原域数据一样，对HSI 梯度域的数据进行奇异值分解，得到的奇异值曲线如图1 中间四幅图所示，均呈明显的衰减趋势。说明梯度域也具有低秩性的特征。从理论上来说，已知

所以，梯度域的秩小于等于原域的秩，因为原域具有低秩性，所以梯度域具有低秩性。因此需要保证梯度域的低秩性。

2.2 LRHSSTV 去噪模型

使用低秩Tucker 分解可以有效地表达HSI 的全局空间和光谱相关性。这里，HSI 原域的低秩特性由Tucker 分解来表现。此外，基于上述分析，HSI 梯度域稀疏特性由LRHSSTV 正则化来说明。同时，采用经典的核范数来表现梯度域的低秩特性。将上述三部分有效结合起来，可以得到LRHSSTV 去噪模型，具体情况如图1。数学形式可表示为

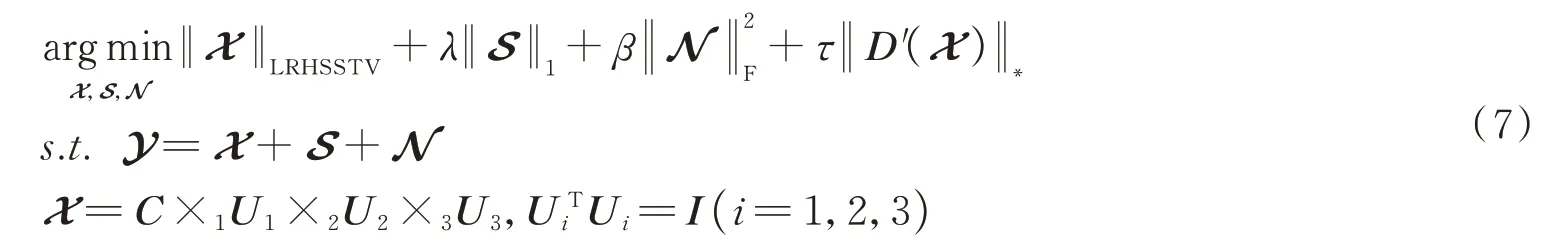
式中，C×1U1×2U2×3U3表示Tucker 分解，其中，C代表分解后的核心张量，Ui表示分解后的因子矩阵；‖ · ‖1表示求取范数，即求各元素之和；表示求取F-范数，即求各元素绝对值平方的开根；λ，β和τ分别表示正则化参数，用于平衡式中正则化项以达到最好的去噪效果。将模型式（7）中的参数W1，W2，β和τ取值为0，模型可以退化为LRTDGS 模型［26］。

2.3 模型求解

由于模型的非凸性，直接求解是非常困难的。本文采用ADMM 的算法框架进行求解。为了计算方便，引入了三个临时变量，分别为Q、H和M，改写后的问题可表示为

式中，W=(W1，W2，W3，W4)，0 ＜Wi＜1，(i=1，2，3，4)；λ，β和τ表示正则化参数，均为大于0 的整数；‖ · ‖1表示求取范数；代表求取F-范数；‖·‖*为求取核范数；；D'=(DvDb，DhDb，Dv，Dh)表示梯度算子。

将模型式（6）的约束优化问题转化成无约束优化问题，可得

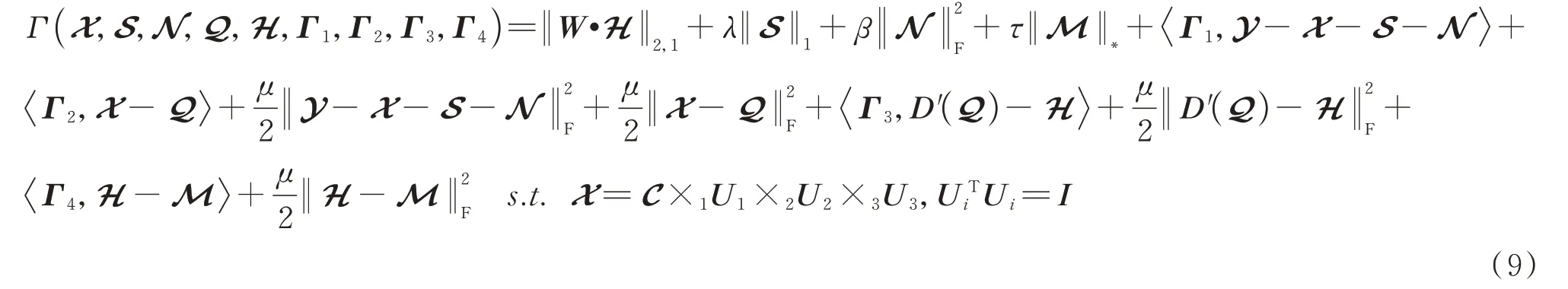
式中，μ表示罚参数；Γi(i=1，2，3，4)表示拉格朗日乘子；根据ADMM 算法，式（7）可以分解成七个子问题分别求解，具体如下：

1）求解C，Ui，X；

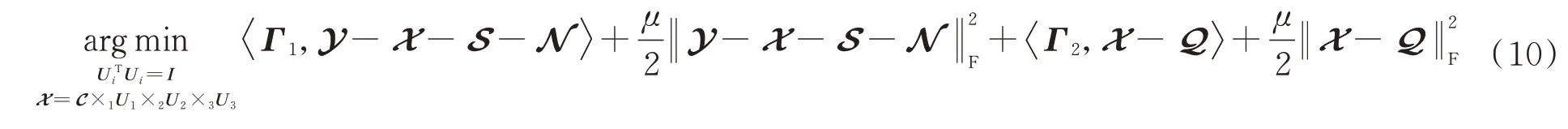
计算合并之后可得

通过使用经典的HOOI 算法［36］，可以求出C和Ui(i=1，2，3)，最终求得

2）求解Q；

计算之后可得

为了求解式（12），需要使用FFT 矩阵［27］，最终得

式中，Tz=|fftn(Dh)|2+|fftn(Dv)|2+|fftn(Dh·Db)|2+|fftn(Dh·Db)|2；fftn 表示快速傅里叶变化；相应地，ifftn 表示快速傅里叶变换的逆变换。

3）求解H；

计算之后，可得

4）求解M；

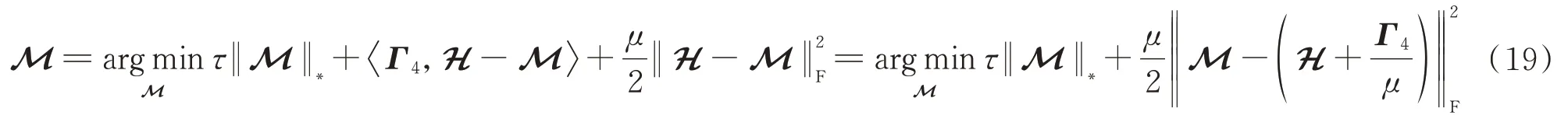
根据文献［34］计算可得

5）求解S；

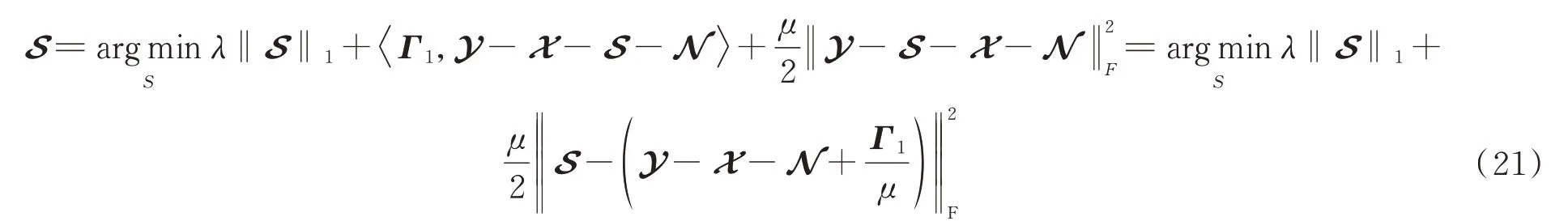
使用软阈值算子［35］计算可得

6）求解N；

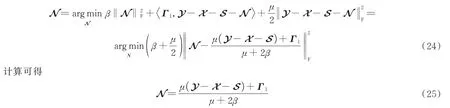
7）更新拉格朗日乘子

式中，参数μ=min(1.5μ，10-5)。

综上所述，LRHSSTV 模型的求解算法：首先，输入噪声HISY，秩[r1，r2，r3]，停止条件ε，正则化参数λ，β，τ和参数μ；初始化变量X，Q，H，M，S，N，Γ1，Γ2，Γ3，Γ4。然后进入迭代循环，基于式（12）和式（15）分别更新X和Q；基于式（18）和式（20）更新H和M；基于式（22）和式（25）更新S和N；采用式（26）更新拉格朗日乘子；直到满足条件或者迭代到最大循环次数跳出循环。最后得到恢复后的HSIX。

2.4 计算复杂度分析

本结综合分析了所提模型的计算复杂度，并给出了每迭代一次计算各个子问题的具体计算复杂度。假设输入的HSI 大小为m×n×p，首先，利用HOOI 算法求解子问题C，Ui和X，主要包括SVD 算法和张量矩阵乘积操作。为了简化分析，假定Tucker 秩为相同的值r，则HOOI 算法的总体计算复杂度为O(mnpr+(m+n+p)r4+r6)。然后，使用FFT 算法求解子问题Q，计算复杂度为O(mnplog(mnp))。此外，使用软阈值算子更新H和S，由于模型在梯度域对HSI 做了四个方向的梯度，所以总的计算复杂度为O(5mnp)。最后，求解M和N，这里主要用到了SVD 算法和点点乘积操作，计算复杂度为O(5mnp)。综上所述，求解本文模型用到的计算复杂度为O(mnpr+(m+n+p)r4+r6+mnplog(mnp)+10mnp)。

3 实验与结果分析

对LRHSSTV 方法进行仿真和真实HSI 数据实验。为了更好地评价新方法的性能，本文将其与最新的7 种HSI 去噪方法（WNNM 方法［28］、LRMR 方法［29］、WSNM 方法［30］、LRTV 方法［31］、BM4D 方法［32］、TDL 方法［33］、LRTDTV 方法［24］）进行比较。在接下来的实验中，这些对比方法所涉及的参数都是根据它们所在文章提供的参数进行选择和调整。此外，为了便于数值计算和可视化，在恢复模型之前将各HSI 波段的灰度值归一化为［0，1］，去噪后的图像再复原到原始水平。另外，针对HSI 的去噪效果，主要采用视觉效果和评价指标相结合的方法进行对比说明。

3.1 模拟数据实验

首先，选择模拟的HSIs 数据进行仿真实验。这些数据是依据Indian Pines 数据集生成的，其大小为145×145×224。在Indian Pines 数据中加入六种不同类型的噪声。具体情况如下：

1）在所有波段加入相同的高斯白噪声，方差为0.1。

2）基于1），在波段91 到130 加入随机数量3 到10 的死线噪声，死线的宽度从1 到3 随机生成。

3）在所有波段加入相同的方差为0.075 的高斯白噪声和百分比为0.15 的脉冲噪声。

4）基于3），在波段91 到130 加入随机数量3 到10 的死线噪声，死线的宽度从1 到3 随机生成。

5）在每个波段加入高斯白噪声，噪声方差在0 到0.2 之间随机选择；同时，加入脉冲噪声，各个波段脉冲噪声的强度在0 到0.2 之间随机选择；另外，在波段91 到130 加入随机数量3 到10 的死线噪声，死线的宽度从1 到3 随机生成。

6）基于5），在波段161 到190 的范围内加入随机条噪声，条带数在20 到40 之间。

从视觉效果来看，图2 和图3 分别给出了噪声1 情况下波段50 和噪声5 情况下波段120 的去噪结果对比图。为了更好地比较不同模型的去噪效果，将所选波段对比明显的同一区域用绿框进行标记，然后在红框中进行放大。从图中可以看出WNNM、LRMR、TDL、WSNM 对高斯噪声去除效果较弱，其中TDL 去噪后仍然存在残余的死线噪声和条带噪声，WNNM 和WSNM 还残存有脉冲噪声。由于WNNM 和LRMR 是基于矩阵操作的，在保持结构完整性上表现较弱，不能很好地处理细节。BM4D 可以达到较好的高斯噪声抑制效果，但是对死线效果不大而且存在过度平滑的现象。LRTV 存在过度平滑的缺点，纹理信息丢失明显。LRTDTV 去噪效果很好，性能明显优于其他方法，但是仍旧存在图像过度平滑现象，图像细节不能完整的保留下来。从图中分析来看，提出的方法去噪效果最好，图像清晰而且结构和细节分明。LRHSSTV 方法既考虑了空间维度也考虑了光谱维度，同时分析了高层之间的内在联系，比起单方向的方法保留了更多的结构特征。同时也将噪声去除的很干净。综合来看，LRHSSTV 方法去噪效果最好。

图2 模拟数据噪声1 情况下第50 通道去噪结果Fig.2 Denoising results on band 50 of simulated data in noise case 1

图3 模拟数据噪声5 情况下第120 通道去噪结果Fig.3 Denoising results on band 120 of simulated data in noise case 5

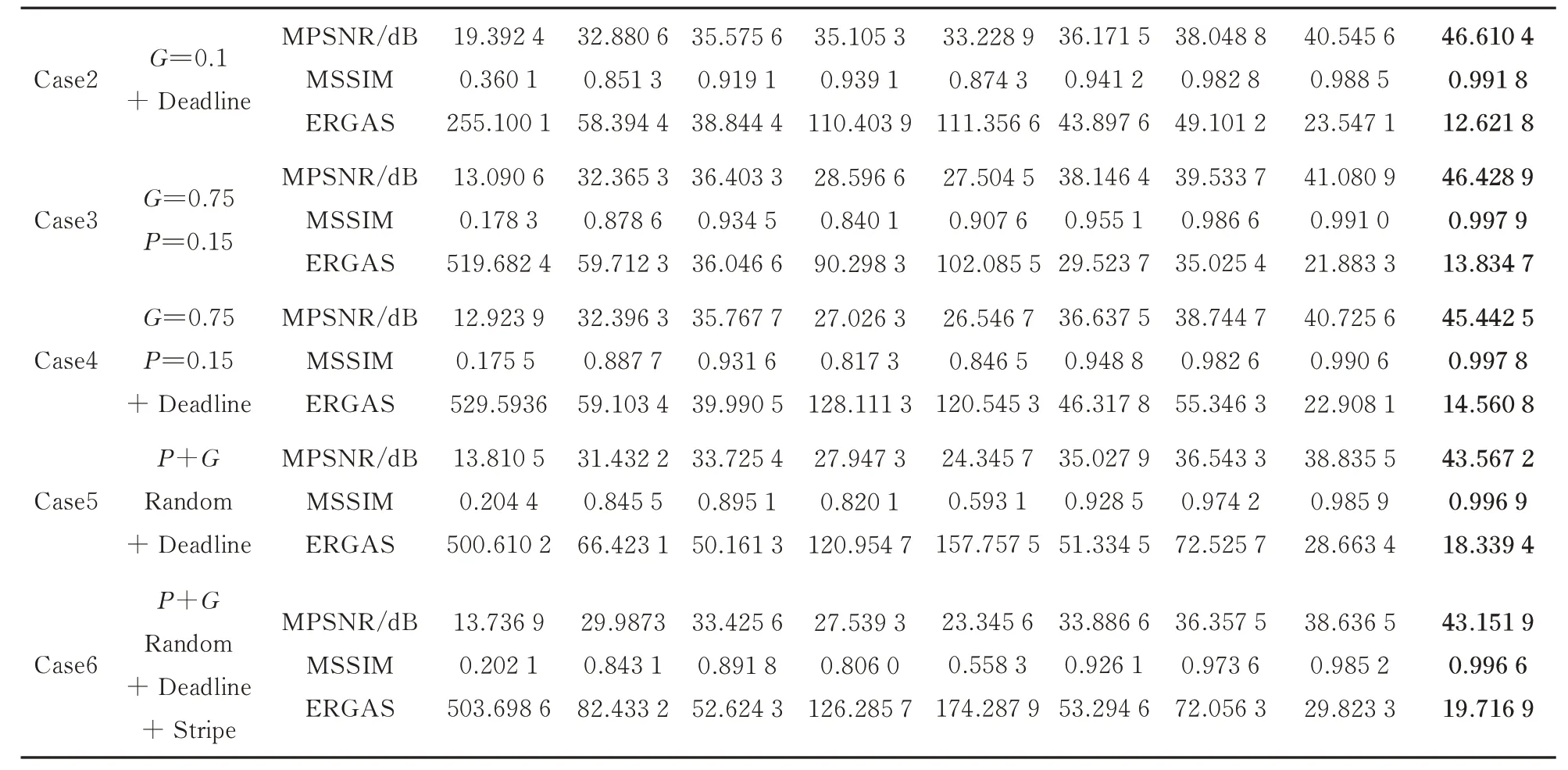
从定量评价指标分析，引入了平均峰值信噪比（MPSNR）、平均结构相似度指数（MSSIM）和全局相对误差（ERGAS）来具体说明。MPSNR 数值越大，MSSIM 数值越大，ERGAS 数值越小说明图像去噪效果越好。表1 展示了在不同噪声情况下不同方法去噪后上述三种图像质量指数（PQIs）的结果，最佳结果都用黑色加粗标注出来了。从表中可以看出，LRHSSTV 方法表现最好。图4 给出了所有方法模拟数据情况下各波段的PSNR 和SSIM 值。可以看出，LRHSSTV 方法在几乎每个波段都可以获得比其他方法更高的SSIM和PSNR 值。综上所述，LRHSSTV 方法在SSIM 和PSNR 上都取得了最好的性能。

图4 模拟数据情况下8 种方法各波段的PSNR 和SSIM 值对比Fig.4 Comparison diagram of PSNR and SSIM values of each band in the case of simulated data

表1 不同噪声情况下各种方法对模拟数据的定性评价结果Table 1 Qualitative evaluation results of various methods on simulated data under different noise cases

3.2 真实数据实验

选用HYDICE 数据集来证明新模型在实际应用中的有效性。这些真实的数据通常含有严重的污染，包括条纹、死线、脉冲噪声、稀疏噪声、高斯噪声等。图5 和图6 分别展示了7 种方法去噪前后波段109 和波段207 的结果。由于TDL 方法去噪效果不明显，与真实噪声图像相差不大，所以在对比图中并未展示。从图中可以看出LRTV 方法由于过度平滑丢失了大量的结构信息，所以去噪效果不好。与其他方法相比，BM4D 方法并没有完全去除死线，条带噪声也很明显。WNNM，LRMR，WSNM，LRTDTV 方法也不能有效去除条带噪声。与它们相比，新方法在去除条带噪声上效果比较明显，同时，细节也保存的相对完整。除了定性的视觉评价，本文也给出了去噪前后的均值剖面图来进行定量评价，如图7，图8。一般而言，均值剖面图波动越小图像质量越高。图7（a）和图8（a）平均剖面波动剧烈，说明图像中存在严重的噪声。在各种去噪模型恢复之后的均值剖面图中，LRTV 具有最光滑的轮廓。然而，LRTV 显然存在过度平滑的现象，丢失了很多有用的信息。BM4D 中的线条仍然波动较大，去噪效果不明显。其余方法均能有效去除噪声，但图像中仍存在局部噪声。相对而言，LRHSSTV 的轮廓是最光滑的，说明其不但能够有效去除噪声，而且保留了更多的细节信息。

图5 真实数据第109 通道去噪结果Fig.5 Denoising results on band 109 of real-word data

图6 真实数据第207 通道去噪结果Fig.6 Denoising results on band 207 of real-word data

图7 HYDICE 数据第109 通道去噪前后竖直均值剖面图Fig.7 Band 109 of HYDICE dataset vertical mean profile before and after denoising via different methods

图8 HYDICE 数据第207 通道去噪前后竖直均值剖面图Fig.8 Band 207 of HYDICE dataset vertical mean profile before and after denoising via different methods

4 参数分析

模型中有三个正则化参数，分别为τ，λ和β。首先将τ固定为1；对于Frobenius 项正则化参数β，一般将其设置为高斯噪声方差的倒数，通过实验分析这里将其设置为10 000；稀疏项正则化参数λ设置为7。

使用Tucker 低秩张量分解来表示HSI 的低秩先验。因此，需要给出估计秩[r1，r2，r3]。通常情况下前两项为空间对应长度的80%。图9 展示了新方法在不同r3值下的MPSNR 值和MSSIM 值。可以很容易地观察到，MPSNR 值和MSSIM 值随着r3值的增大先增大后减小。因此，实验选取峰值时的r3值。

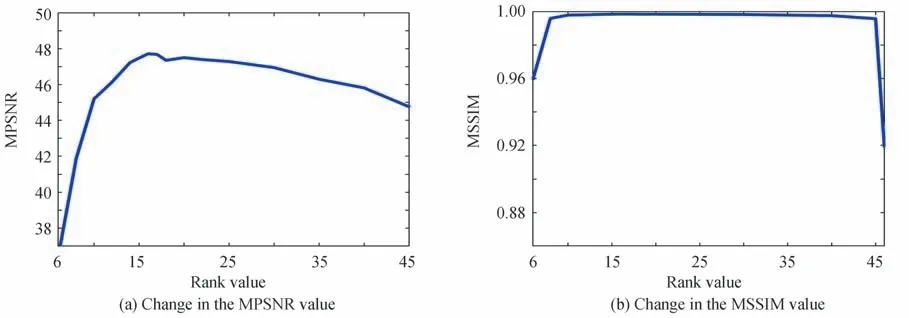
图9 随着r3 值增加MPSNR 和MSSIM 值的变化图Fig.9 The change diagram of MPSNR and MSSIM value as the value of r3 increases

图10 出了新方法随着迭代次数的增多MPSNR 值和MSSIM 值的变化。实验发现经过多次迭代后，MPSNR 值和MSSIM 值都趋于稳定，体现了算法的收敛性。

图10 随着迭代次数增加MPSNR 和MSSIM 值的变化图Fig.10 The change diagram of MPSNR and MSSIM value as the number of iterations increases

5 结论

本文从HSI 的稀疏和低秩先验两方面来研究HSI 去噪问题。引入了高阶梯度，充分挖掘了高阶差分各方向之间的内在联系，提出了加权的1,2范数来探索梯度域稀疏。同时利用核范数最小化和张量Tucker 分解来探索高光谱图像在梯度域和原域上的低秩特征。通过对先验信息进行约束，模型更全面地挖掘了HSI的特征。此外，采用ADMM 算法对所提模型进行求解。通过仿真和真实数据实验，证明了新方法在实际应用上的可用性和优越性。与其他方法相比，在Indian Pines 数据集上本文模型复原结果的平均峰值信噪比提高了5.35 dB，平均结构性相似指标提高了0.009。从去噪结果来看，本文模型使去噪图像在保持主体信息的同时，保留了更多的图像纹理细节。未来，将进一步优化模型，研究HSI 在原域和梯度域中的更多特征，增强其在真实场景中去除更复杂噪声的能力。