校谱线弯曲的共轴PGP成像光谱仪光学系统设计
樊星皓,刘春雨,徐明林,刘帅,赵英明,崔亚珍
(1 中国科学院长春光学精密机械与物理研究所,长春 130033)
(2 中国科学院大学,北京 100049)
(3 中国科学院天基动态快速光学成像技术重点实验室,长春 130033)
0 引言
成像光谱仪是一种能同时获得目标光谱信息、辐射信息和空间信息的光学遥感仪器,具有图谱合一的优点[1-2]。因此,在地球资源普查、地面测绘、环境监测、医疗器械、自然灾害的检测与预警等方面有着重要的应用[3-6]。
棱镜和光栅是成像光谱仪最常用的分光元件,但是棱镜型和光栅型成像光谱仪的光路为离轴系统,存在装调困难、稳定性不足等问题[7-8]。基于棱镜-光栅-棱镜(Prism-Grating-Prism,PGP)组合色散元件的成像光谱仪拥有衍射效率高、光路共轴等优点,其组合色散元件由左右两块棱镜和中间的体相位全息光栅组合而成。两个棱镜的作用是抵消光栅的衍射角度,使得某一波长的出射光束与入射光束处于同一轴线,从而使PGP 成像光谱仪整体上为方便安装的共轴结构。
AIKIO M 最早将PGP 组合色散元件应用于机载成像光谱仪(Airborne Imaging Spectrometer for different Applications,AISA),并论述了PGP 成像光谱仪的特点[9-10]。RASMUS N J 指出了PGP 成像光谱仪存在较大的、会影响光谱探测准确性的谱线弯曲,并提出采用电子标定方法校正谱线弯曲[11]。国内的李哲[12]使用了类似的标定方法校正了光谱仪的谱线弯曲。但是电子标定方法无法解决谱线弯曲造成的探测器使用效率下降的问题,也在一定程度上加大了图像处理的复杂性。
在设计上,中国科学院西安光学精密机械研究所、苏州大学和中国科学院长春光学精密机械与物理研究所等先后对PGP 光谱成像仪进行研究和改进[13-20]。2014 年,中国科学院长春光学精密机械与物理研究所的张晓龙[15]提出了引入离轴透镜的方法补偿校正谱线弯曲,但是该方法增加了光路的复杂性;杨增鹏[13]和陈洪福[16]利用棱镜和光栅的谱线弯曲方向相反的特性,采用棱镜-光栅(PG)的组合方式校正了谱线弯曲,但打破了PGP 光路的共轴性。2021 年,该机构的李伟[19]使用球面反射镜配合PG 结构降低了谱线弯曲,但同样打破了PGP 光路的共轴性,增加了装调难度。同年,中国科学院国家空间科学中心的武志昆[20]通过降低第一个棱镜的顶角配合狭缝离轴的方式在保证光路共轴性的同时,校正了谱线弯曲,但是该光谱仪的狭缝长度仅为9 mm,视场较小。为了实现大视场共轴PGP 光谱仪谱线弯曲(smile)的校正,还需探索其他方法。
2020 年,中国科学院长春光学精密机械与物理研究所的张嘉伦[21]在offer 光谱仪的设计中,为了克服长狭缝的谱线弯曲问题,使用了弯曲狭缝,取得了比较好的效果,但是并没有给出弯曲狭缝形状的计算方法。基于此,本文将论证采用弯曲狭缝的方式校正共轴PGP 成像光谱仪中谱线弯曲问题的可行性,并拟给出共轴PGP 成像光谱仪弯曲狭缝形状的一般计算方法。
本文首先建立了PGP 矢量色散模型,分析成像光谱仪各个要素对谱线弯曲大小的影响。然后,根据分析结果,确定共轴型PGP 分光元件的谱线弯曲特点,指出引入弯曲狭缝的必要性,并提出狭缝弯曲形状配合镜头畸变校正谱线弯曲的一般方法。最后,利用遗传算法快速确定狭缝弯曲形状和镜头畸变的最佳参数组合,并设计了一套光学系统验证该方法的可行性。
1 工作原理
PGP 成像光谱仪结构如图1 所示,由狭缝、准直镜、PGP 组合色散元件、聚焦镜和探测器组成。望远物镜将来自目标的光线会聚在狭缝处,狭缝作为成像光谱仪的视场光阑,只允许落在狭缝内的光线进入PGP成像光谱仪,经狭缝入射的光线经过准直镜准直为平行光后进入PGP 组合色散元件。不同波长的光线被PGP 色散成为不同角度的平行光,最后通过聚焦镜会聚在探测器上形成光谱。

图1 PGP 成像光谱仪的工作原理Fig.1 The working principle of PGP imaging spectrometer
成像光谱仪的谱线弯曲(smile)被称为“微笑畸变”,是由主截面光束和非主截面光束之间的色散差异造成的[20]。狭缝中心的光束在棱镜和光栅的主截面上入射,狭缝其他位置的光束则在非主截面上入射,故狭缝像会在光谱维方向产生形变,如图2 所示。从图中可以看出,谱线弯曲会使探测器的同一行像素接收到多个通道的光谱能量,从而增加成像光谱仪光谱提取的难度;另外,探测器的左上角、右上角和下面中间部分像素无法被利用,会降低探测器的使用效率。

图2 弯曲的狭缝像在探测器上的成像示意图Fig.2 Schematic image of the curved slit on the detector
2 PGP 矢量色散模型
2.1 模型建立
光束在分光元件上的入射角度、棱镜的材料、棱镜的角度和光栅的刻线数等都对谱线弯曲有影响,为了定量分析各个因素对谱线弯曲的影响情况,探讨谱线弯曲的改善方法,需要建立基于PGP 组合色散元件的矢量色散模型。
来自狭缝任意一点的光束经过准直镜准直后入射到PGP 组合色散元件上的光路情况如图3 所示,光束先后经过棱镜1 折射、光栅衍射和棱镜2 折射后出射。

图3 PGP 组合色散元件中的光路示意图Fig.3 Schematic diagram of optical path in PGP combined dispersive element
因为玻璃材料对不同波长λ的光的折射率有所区别,所以不同波长的光经棱镜折射后光矢量方向也会有所差别,而经光栅衍射后这种方向上的差别还会进一步增大。为了方便叙述,将经过某一界面折射或者衍射后的波长为λ的光矢量统一表示为Li(λ)。图3 中L0为来自狭缝的入射光束的光矢量,为方便研究,取L0为单位向量,向量方向由光束的入射角度θ决定,可以表示为

光矢量L0入射到PGP 组合色散元件上,先后在各个界面发生折射,根据矢量折射定律,折射前的光矢量Li(λ)与折射后的光矢量Li+1(λ)的关系为[13]

式中,ni和ni+1分别为光束在第i个界面处的入射介质和出射介质的折射率,Ni为第i个界面的法向量,αi和α'i分别为光束在界面i处的入射角和折射角。其中,Ni和棱镜的角度βi有关,而αi则同时受Li(λ)和Ni的影响,因此,Ni和αi可以表示为

光束在经过光栅界面后的传播方向主要由光栅的衍射特性决定,任意空间角度的入射光线在平面光栅上衍射的普适光栅方程为[13]
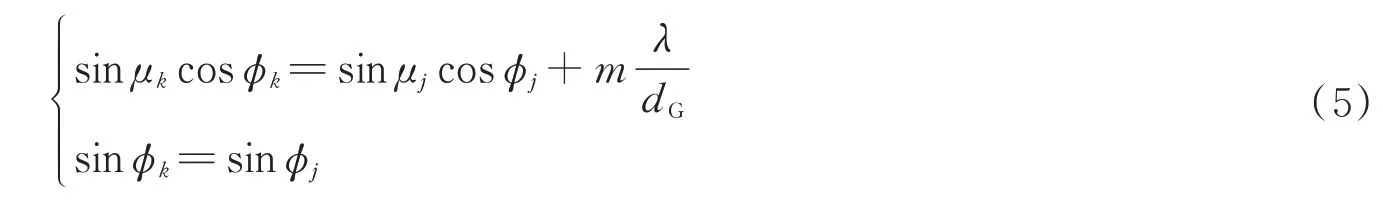
式中,μj为光线的入射角,μk为光线的衍射角,均为光矢量在子午面内的投影与光栅法线的夹角;ϕj为光线的入射方位角,ϕk为光线的衍射方位角,均为光矢量与主截面的夹角;λ为入射波长,dG为光栅常数,m为衍射级次。
采用光栅的+1 级衍射,光束经光栅衍射后继续向前传播,最终不同波长的光束沿光矢量L5(λ)所表示的方向出射。联立式(1)~(5),可以得到出射光矢量L5(λ)是(λ、β1、β2、dG、θ、n1、n2、n3)的函数。为方便描述,令L5(λ)在子午面和弧矢面的投影角度分别为ξt和ξs,如图3 所示。
为满足PGP 成像光谱仪的光路共轴特性,需控制参数,以保持氦氖激光器的光(632.8 nm)能直视通过光学系统,方便装调过程。即参数(β1、β2、dG、n1、n2、n3)需要满足

式中,θ0为狭缝中心的光束在PGP 上的入射角度,即θ=0 时,波长为632.8 nm 的光束经过PGP 组合色散元件后传播方向不发生改变。
2.2 谱线弯曲与目标函数
谱线弯曲表现为狭缝像在探测器上的弯曲现象,其弯曲量的大小可以用狭缝端点的光束和狭缝中心的光束在探测器光谱维方向上交点的差值来表示[16]。假设准直镜和聚焦镜的焦距均为f',则在该模型中,不同波长λ的谱线弯曲大小可以表征为
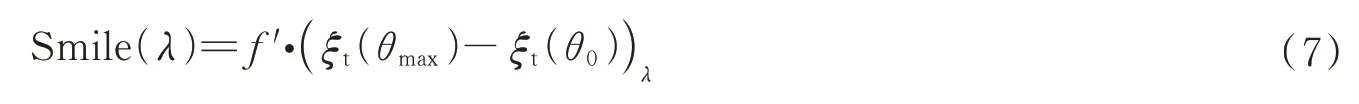
式中,θmax为来自狭缝边缘的光束在PGP 上的入射角度。
因为出射光矢量L5(λ)是(λ、β1、β2、dG、θ、n1、n2、n3)的函数,所以可以推得式(7)中Smile(λ) 是(f'、λ、β1、β2、dG、θmax、n1、n2、n3)的函数。为了简化分析过程,忽略影响微弱的折射率ni,着重研究λ、β1、β2、dG和θmax对谱线弯曲的影响,且为方便计算,棱镜和光栅的保护玻璃均取为H-K9L。
经分析可知,在满足式(6)共轴条件时,β1、β2、dG的任意组合均不能满足消除谱线弯曲的条件。图4 给出了光栅刻线数在280 lp/ mm、聚焦镜焦距为80 mm 时的分析实例,展示了该参数下中心波长(600 nm)的光在不同棱镜角度β1、β2组合下的谱线弯曲情况。从图中可得:1)当棱镜角度和光栅常数满足一定条件时,能够消除中心波长的谱线弯曲,如图中蓝色虚线所示;2)消除中心波长谱线弯曲时β1、β2的集合和满足光路共轴条件时的β1、β2没有交集,即满足式(6)共轴条件时PGP 成像光谱仪在中心波长处不可避免地具有较大的谱线弯曲,如图中红色实线所示;3)光线在PGP 上的入射角度对谱线弯曲影响较大,减小光线入射角度θmax虽然可以在一定程度上降低谱线弯曲的大小,但同样无法消除谱线弯曲。

图4 光栅刻线数为280 lp/ mm 时的谱线弯曲Fig.4 The smile when grating line is 280 lp/ mm
因此,可以认为中心波长的谱线弯曲是共轴PGP 成像光谱仪的固有问题,无法通过改变β1、β2、dG组合的方式校正,同时,也无法通过改变入射光线的角度θ来校正该谱线弯曲。
为了进一步研究其他波长的谱线弯曲情况,令狭缝长度为22 mm,准直镜和聚焦镜的焦距均为80 mm,通过PGP 矢量色散模型对400~800 nm 波长的狭缝像进行分析,结果如图5、6 所示。其中,图6 给出了狭缝像在探测器上的成像情况,并用弯曲量Δy(λ,l)代替了Smile(λ),从而更好地描述狭缝所有位置的谱线弯曲情况。在分析时,取棱镜1 角度为9.27°,棱镜2 角度为10.26°,此时满足光栅的布拉格衍射条件,衍射效率最高[12]。

图5 400~800 nm 工作波段的谱线弯曲情况Fig.5 The smile from 400~800 nm

图6 探测器上的狭缝像Fig.6 The slit image on the detector
从图5 可以看出,PGP 成像光谱仪的狭缝像在400~800 nm 工作波段内均弯向短波方向,且波长越短,弯曲量Δy(λ,l)越大。从图6 可以看出,当狭缝像均弯向短波方向时,较难处理,例如通过聚焦镜的畸变难以校正所有波长的谱线弯曲。因此,拟用弯曲狭缝来改变不同波长狭缝像的弯曲情况,从而改善狭缝像在工作波段内均弯向短波方向的问题,为谱线弯曲的校正创造条件。弯曲狭缝的形状可由狭缝在0.25L、0.5L、0.75L和L处的弯曲量h1、h2、h3、h4表示,如图7 所示。

图7 弯曲狭缝示意图Fig.7 Schematic diagram of curved slit
从图5 和6 可以知,为了校正谱线弯曲,狭缝应弯向长波方向,并且弯曲狭缝的形状选择也较为关键。如果只根据PGP 成像光谱仪的固有谱线弯曲大小来设置狭缝形状,则谱线弯曲的校正效果并不理想。例如,图5 中600 nm 波长(中心波长)处的谱线弯曲可以拟合为半径为198 mm 的圆弧,如果用此处的谱线弯曲来决定狭缝形状,则狭缝应当是一个半径为198 mm、与图7 中x轴相切、弯向长波方向的圆弧。此时,光谱仪的谱线弯曲情况如图8 所示。
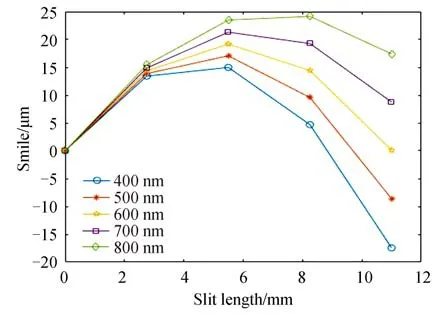
图8 圆弧形狭缝在400~800 nm 工作波段的谱线弯曲情况Fig.8 The smile of the circular slit from 400 nm to 800 nm
从图中可以看出,400~800 nm 的谱线弯曲情况有所缓解,其中600 nm 狭缝边缘处的谱线弯曲基本得到了校正,而其他波长相对于600 nm 波长有较大的谱线弯曲剩余。另一方面,0.25L、0.5L、0.75L处每个波段均有较大的谱线弯曲剩余,说明该狭缝形状并非最优解。
为了进一步校正剩余的谱线弯曲,需要适当调整弯曲狭缝的形状,并改变准直镜、聚焦镜的畸变等光学参数,还要考虑镜头畸变带来的光谱弯曲(keystone)等问题。如果直接使用Zemax 软件对系统进行校正谱线弯曲的优化,则容易陷入局部极小值,难以实现最优解。另外,Zemax 软件不容易对狭缝形状进行直接优化,需要在优化时根据经验手动调节狭缝的形状,因此成像光谱仪光学系统的优化过程可能需要较多时间,并且要求工作人员有较丰富的设计经验。
为了避免在设计时陷入局部极小值,并开发一种校正谱线弯曲的普适性方法,拟用遗传算法来快速确定狭缝弯曲形状和镜头畸变的最佳参数组合,并将该最佳参数组合作为初始结构输入到Zemax 软件中进行设计和验证。
2.3 遗传算法
遗传算法是一种模拟生物进化过程的智能算法。它适用于多维变量的优化过程,具有良好的全局搜索能力[22]。
使用遗传算法首先要建立目标函数,将实际问题转换为可以量化表示的数学表达式。在对校正谱线弯曲的共轴PGP 成像光谱仪的初始结构选择时,需要着重注意的是狭缝形状和镜头畸变等参数对谱线弯曲和光谱弯曲的影响。其中谱线弯曲是光谱在光谱维方向的形变,而光谱弯曲是光谱在空间维方向的形变,因此,在建立目标函数时,应尽可能使光谱在光谱维和空间维的形变均为零。
拟采用弯曲狭缝形状和镜头的畸变相互配合的方式来寻求一种谱线弯曲的校正,校正思路如图9 所示。其中,狭缝形状、准直镜畸变、聚焦镜畸变相互影响,在目标函数建立时需要对这些参量进行耦合分析。
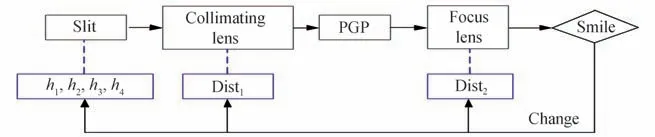
图9 校正谱线弯曲成像光谱仪的设计流程Fig.9 Flow chart of the design of the eliminate smile imaging spectrometer
聚焦镜的畸变Dist2会使狭缝像在空间维产生Δx2的位移,在光谱维产生Δy2的位移,如图5 所示。而准直镜的畸变Dist1会使狭缝像在空间维产生Δx1的位移,在光谱维产生的位移趋近于零,可忽略不计。调整Dist1和Dist2的大小使Δx1+Δx2=0,则准直镜和聚焦镜的组合只影响狭缝像的弯曲量Δy(λ,l),而不影响狭缝像在空间维的长度。因此,波长为λ的狭缝像在狭缝长度为l处的弯曲量Δy(λ,l)可以表示为

而波长为λ的狭缝像相比于狭缝在空间维上的偏移量Δx可以表示为

当Δx(λ)=0 时,狭缝像在空间维没有形变,即没有光谱弯曲。
经过上述分析,谱线弯曲的校正过程需要综合调节弯曲狭缝的形状h1、h2、h3、h4和镜头的畸变Dist1、Dist2,且谱线弯曲的大小与波长λ紧密相关。选取400 nm、500 nm、600 nm、700 nm 和800 nm 共5 个波长进行分析,考察其狭缝像的弯曲情况。因此,目标函数可以表示为

式中,Fm为PGP 成像光谱仪狭缝像弯曲情况的综合反映,其值越小表示系统谱线弯曲越小;wij与wk为相应项的权重。因此,通过建立目标函数可以将寻找狭缝形状和镜头畸变的最佳组合问题转化为寻找目标函数Fm的最优解问题。
用遗传算法对目标函数Fm进行优化,具体过程为:
1)编码和初始化种群。首先,将参数h1、h2、h3、h4、Dist1、Dist2在一定范围内随机取值,并组成一个编码串,每个编码串代表一个潜在解。其中,参数被称为基因,由这6 个参数组成的编码串被称为染色体。然后,随机产生多个染色体。可以认为每个个体携带一个染色体,而所有个体组成初始种群N。
2)计算适应度值和自然选择。首先,计算每条染色体的计算适应度值,用来评价每个个体的优劣。在本算法中,令适应度函数fit 满足

目标函数值越小,个体的适应度值越大。然后,使用转盘法对所有个体进行选择。转盘法的选择是一种概率选择,评分高的个体被选中的概率更高,为了避免良好基因被排除,评分低的个体也有一定机会入选。
3)交叉与变异。被选中个体所携带的染色体按一定的概率进行交配,即染色体上的对应基因按一定的概率进行交换。然后,某些个体的基因按照设定的概率进行变异,产生子代染色体。之后携带子代染色体的个体组成新的种群,并按照相同的方式产生下一代种群。
4)终止条件和输出。终止条件通常为算法所设定的最大进化代数或者适应度函数值是否若干代没有变化。若不满足终止条件,则返回第2)步;若满足条件则输出参数。整个过程的流程如图10 所示。

图10 遗传算法的流程Fig.10 Flow chart of genetic algorithm
令式(10)中的wij与wk均为5,迭代优化50 代,优化后的几种参数组合以及它们的适应度值如表1 所示。

表1 狭缝形状与镜组畸变的组合参数Table 1 Combined parameters of slit shape and lens distortion
注意到四种结构的适应度函数值虽有不同,但Dist1基本均为Dist2约0.75 倍,这是准直镜和聚焦镜的视场大小不同所导致的。准直镜和聚焦镜的视场将在3.2 节中详细分析。选取表1 中的第一行作为校正谱线弯曲PGP 成像光谱仪狭缝形状和镜头畸变的初始结构,计算了该初始结构的谱线弯曲情况,如图11 所示。

图11 弯曲狭缝的PGP 光谱仪的谱线弯曲Fig.11 Smile of PGP spectrometers with the curved slit
通过比较图5 和图11 可知,弯曲狭缝PGP 成像光谱仪能大幅降低谱线弯曲,通过弯曲狭缝和镜头畸变相互配合的方式,能将-140 μm 大小的谱线弯曲量控制在1.2 μm 以内。
该校正共轴PGP 成像光谱仪谱线弯曲的方法虽然引入了弯曲狭缝,但是保证了光谱仪光路的共轴,有利于仪器的紧凑化。并且,该方法所使用的PGP 矢量色散模型充分考虑了各种因素对谱线弯曲的影响,能够胜任任意光栅常数的PGP 成像光谱仪谱线弯曲校正,如表2、表3 所示。

表2 光栅刻线数为280 lp/mm 的组合参数Table 2 Combined parameters when grating line is 280 lp/mm

表3 光栅刻线数为250 lp/mm 的组合参数Table 3 Combined parameters when grating line is 250 lp/ mm
保持光栅刻线数为280 lp/mm,准直镜、聚焦镜的焦距为80 mm 不变,改变狭缝长度。当狭缝长度增加到30 mm、40 mm 时,遗传算法也能给出合适的参数组合,将谱线弯曲控制在1.79 μm 以内,如表2 所示。即弯曲狭缝配合镜头畸变校正smile 的方法对不同长度的狭缝具有普适性。而表3 则证明了该方法对于不同光栅常数的共轴PGP 成像光谱仪具有普适性。
从表2 和表3 可以看出,当狭缝长度增大到50 mm 时,虽然剩余smile 变大,但是仍能将直狭缝大于600 μm的谱线弯曲控制在4.7 μm 左右,对超长狭缝共轴PGP 光谱仪的设计具有一定的指导意义。
3 成像光谱仪的设计
3.1 设计指标
结合应用需求,设计了一台工作波段为400~800 nm 的共轴 PGP 成像光谱仪,光栅基底材料和棱镜材料均选用 H-K9L,狭缝长度定为22 mm,棱镜1 角度为9.27°,棱镜2 角度为10.26°。该共轴PGP 成像光谱仪的主要设计指标如表4 所示。

表4 成像光谱仪的主要设计指标Table 4 The main indexes of imaging spectrometer
3.2 准直镜与聚焦镜
成像光谱仪的准直镜和聚焦镜均采用焦距为80 mm、F数为3.5 的镜头。准直镜和聚焦镜的视场分别受狭缝长度l和像面大小(空间维长度H×光谱维长度V)的影响,即

式中,w1与w2分别为准直镜和聚焦镜的视场角,fz为准直镜的焦距,fj为聚焦镜的焦距,b为狭缝长度;H为像面空间维的长度,由于准直镜和聚焦镜的焦距相等,故数值上H=b=22 mm;V为像面光谱维的长度,其数值大小由光线在光谱维的色散角度和聚焦镜的焦距共同决定。由PGP 的矢量色散模型可知,400 nm 光束的光谱色散角度约为-3.77°,800 nm 光束的光谱色散角度约为2.72°,可以计算得到像面光谱维的长度V=9.07 mm。故由式(12)可知准直镜和聚焦镜的视场角分别为2w1=15.7°和2w2=20.2°
在设计准直镜和聚焦镜时,应该使准直镜的最大畸变接近-0.9%,聚焦镜的最大畸变接近-1.16%。为确保PGP 成像光谱仪与前端望远物镜达到光路匹配,要求成像光谱仪准直镜的光路为物方远心光路。在实际设计中,准直镜采用反向设计,即设计为像方远心光路,如图12 所示。而聚焦镜无需使用像方远心结构,从而减小限制条件以方便系统像差的校正,其初步优化结果如图13 所示。

图12 准直镜的光路结构Fig.12 Optical path diagram of collimator lens

图13 聚焦镜的光路结构Fig.13 Optical structure diagram of the focusing lens
3.3 整体优化
各部分设计完成后,将准直镜、聚焦镜和 PGP 组合色散元件的结构参数输入ZEMAX 中,在软件中进行光路拼接。拼接时注意使PGP 元件恰好位于准直镜和聚焦镜的光阑位置,这样被PGP 色散的不同波长的光束都恰好能充满聚焦镜的光瞳。
拼接完成后,在ZEMAX软件中根据h1、h2、h3、h4这4 个弯曲狭缝的形状参数设置系统的视场。本系统所用的狭缝参数如表1 中序号1 所示,根据狭缝参数,该弯曲狭缝的形状可以拟合为式(13)所示的多项式。目前的加工工艺可以对这种4 次项多项式表示的狭缝进行高精度加工,其实际加工效果如图14 所示。

图14 弯曲狭缝加工示意图Fig.14 Schematic diagram of processed curved slits
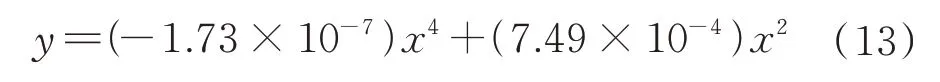
在软件中完成系统的视场设置后,用RAGX、RAGY 等操作数将Δx(λ)和Δy(λ,l)的优化目标设置为0,从而限制光学系统谱线弯曲和光谱弯曲的大小。把点列图和调制传递函数(Modulation Transfer Function,MTF)的大小作为镜头成像质量的评价指标,对光学系统进行优化以提高其成像质量。PGP 成像光谱仪光学系统的最终优化结果如图15 所示。该PGP 成像光谱仪光栅刻线数为280 lp/mm、棱镜1 角度为9.27°,棱镜2 角度为10.26°,系统共使用13 片玻璃,包络尺寸为180 mm×28 mm×28 mm。

图15 PGP 光谱仪的光学结构Fig.15 Optical structure diagram of the PGP spectrometer
3.4 像质评价
在ZEMAX 中对3.3 节中的PGP 成像光谱仪进行了谱线弯曲分析,该光谱仪使用的狭缝形状如式(13)所示。分析结果表明,设计的弯曲狭缝PGP 成像光谱仪具有较强的校正谱线弯曲的能力,其在400~800 nm的谱线弯曲均小于1 μm,且在0.091 个像元以内。该成像光谱仪各视场的光谱弯曲均小于0.7μm,且小于0.7个像元,如图16 和17 所 示。

图16 PGP 光谱仪的谱线弯曲Fig.16 Smile of PGP spectrometer
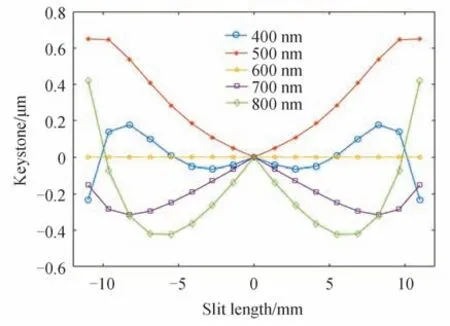
图17 PGP 光谱仪的光谱弯曲Fig.17 Keystone of PGP spectrometer
图18 给出了该光学系统狭缝像的点列图情况,图中每个方格代表一个探测器的像元大小,结果显示,系统对间隔为2 nm 的狭缝像具有良好的区分能力,故能满足2 nm 光谱分辨率的设计要求。图19 则给出了该光学系统在不同波长下弥散斑的均方根半径情况。结果显示,在400~800 nm 波长范围内,经过狭缝不同位置的光线在像面上的弥散斑半径均不大于5.4 μm,能满足成像要求。

图18 系统的点列图Fig.18 Spot diagrams
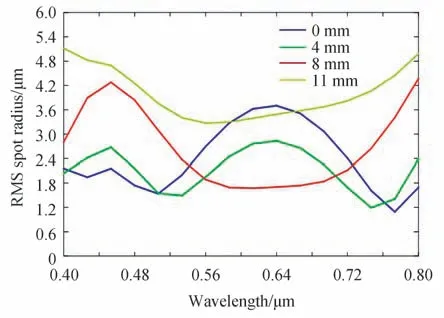
图19 点列图半径的均方根值随波长的变化关系曲线Fig.19 RMS spot radius versus wavelength
图20 为该光学系统的衍射能量集中度曲线,其中横坐标为距离像点质心距离,纵坐标表示一定范围内能量所占总能量的比例,不同颜色曲线则表示不同狭缝位置的情况。可见,所有视场的能量集中度在2×2像元包围框内均达到90%,符合设计要求。

图20 能量集中度曲线Fig.20 Energy concentration diagram
MTF 能够全面反映光学系统的成像质量,图21 给出了400 nm、600 nm 和800 nm 波长在Nyquist 频率45.5 lp/ mm 处的调制传递函数情况。从结果可见,800 nm 波段在Nyquist频率处的MTF 值均优于0.6;400 nm和600 nm 波长在Nyquist 频率处的MTF 值优于0.4,像质良好,满足成像质量要求。

图21 多个波段的调制传递函数曲线Fig.21 The modulation transfer function of multiple wavelengths
3.5 小结
分析可知,弯曲狭缝对于矫正光谱仪的谱线弯曲和光谱弯曲有较好的效果,但有利也有弊,弊端是此弯曲狭缝光谱仪与望远物镜联合使用时,可能会导致观测的瞬时视场与探测器像元存在几何配准问题。如果狭缝与谱线(狭缝像)都是平直的,则探测器获得的数据可以直接使用;如果狭缝平直而谱线弯曲,则需要进行光谱定标,对谱线进行校正;如果狭缝弯曲而谱线平直,则需要将探测器的谱线与狭缝进行几何配准,图22 和23 给出了狭缝平直谱线弯曲和狭缝弯曲谱线平直的两种情况。

图22 平直狭缝与弯曲谱线的对应关系Fig.22 The correspondence between straight slit and curved spectral lines
图23 中,Y400、Y405分别为狭缝中心点在400 nm、405 nm 所对应像点在探测器上的ysp坐标大小;ysp=A1x3+B1x2+C1x+Y400和ysp=A2x3+B2x2+C2x+Y405分别表示400 nm 狭缝像和405 nm 狭缝像的弯曲程度,因为不同波长的谱线弯曲大小不同,因此A1与A2、B1与B2、C1与C2的值并不相同,在光谱定标时,每个通道的谱线弯曲情况要进行分别标定和校正,光谱仪的通道数一般在100 个以上,工作量很大。另外,从400 nm 和405 nm 的狭缝像可以看到,存在同一个像元承接相邻两个谱段狭缝像的情况,会影响数据准确性。
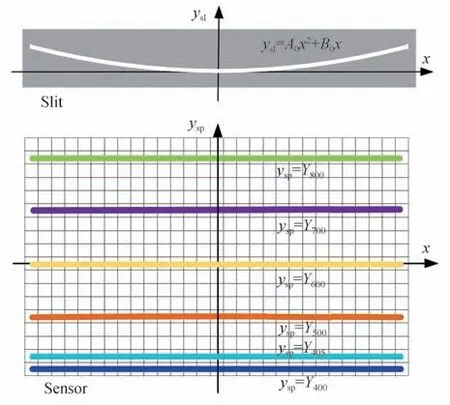
图23 弯曲狭缝与平直谱线的对应关系Fig.23 The correspondence between curved slit and straight spectral lines
弯曲狭缝对应的狭缝像是平直的,如果将探测器获得的数据不加校正直接使用,那狭缝边缘的目标会被认为与中心目标在同一直线上,即图像数据与目标实际空间位置并不相同,类似于畸变。能够注意到任意光谱通道与弯曲狭缝的对应关系都是相同的,因此可以通过弯曲狭缝的表达式ysl=A0x3+B0x2+C0x进行数据修正(几何配准),使探测器上的数据点回归正确的空间位置,即对空间维进行校正。通过两种方法的比较可得,弯曲狭缝的几何配准更简单一些,且光谱的准确性更高。
另一方面,弯曲狭缝在制作时,采用飞秒激光设备对薄金属材料进行微米级加工。首先根据表达式在电脑中画出弯曲狭缝的图形,然后激光设备在加工时对电脑设计好的图形进行走位,以达到弯曲狭缝的效果。在设计时狭缝各处在ysl方向的宽度相同,即在推扫方向上边缘区域和中心区域对应的地面分辨率相同,因此在推扫时能实现条带区域的全覆盖,如图24 所示。在狭缝加工完成后使用二次元测量仪对狭缝的轮廓进行检测,以保证狭缝的加工精度,二次元测量仪和狭缝在仪器下的检测实拍图分别如图25 和26所示。

图24 弯曲狭缝的推扫示意图Fig.24 The push process of curved slit

图25 二次元测量仪Fig.25 Quadratic element measuring instrument

图26 狭缝测量结果Fig.26 Slit measurement results
为了将本文使用了弯曲狭缝的PGP 成像光谱仪与其他类型的成像光谱仪相比较,引入了筒长狭缝比和体积狭缝比的概念。文献[13]中的系统与本文设计的成像光谱仪相似,不过该文献中的利用的是棱镜和光栅的谱线弯曲相反的特点校正了谱线弯曲,该仪器的尺寸大小约为175 mm×33 mm×33 mm,狭缝长度为14 mm,筒长与狭缝长度的比值为12.5,而本文中仪器筒长与狭缝长度的比值为8.2,因此,在相同的筒长下,采用本文设计的光谱仪的狭缝更长,采用相同望远物镜时能实现更大的视场。
文献[23]中的系统为offer系统,能够实现40 mm的长狭缝设计,系统的尺寸为310 mm×220 mm×125 mm,筒长与狭缝长度的比值更小,为7.75。但是offer 系统是一种离轴反射结构,体积较大,如果评价成像光谱仪体积与狭缝长度的比值的话,文献[23]中系统数值比值为213 125,而本文中的系统该数值比值为6 414。综合来看,采用了弯曲狭缝的PGP 成像光谱仪更加紧凑,更容易实现小型化。
4 结论
本文提出了利用弯曲狭缝配合准直镜和聚焦镜畸变的方法校正共轴PGP 成像光谱仪谱线弯曲的设计思路,给出了普适性的设计方法,并证明了该方法的可行性。通过建立的PGP 矢量色散模型分析得到PGP在满足光路共轴条件下一定会产生较大的谱线弯曲,阐明了使用弯曲狭缝校正共轴PGP 成像光谱仪的必要性。利用遗传算法确定了狭缝弯曲形状的数学表达式和准直镜、聚焦镜畸变的大小,并设计了一个狭缝长度为22 mm,工作波段为400~800 nm,光谱分辨率为2 nm,F数为3.5 的弯曲狭缝PGP 成像光谱仪光学系统,该系统谱线弯曲小于1 μm,光谱弯曲小于0.7 μm。
该方法在校正谱线弯曲的基础上保留了PGP 成像光谱仪的光路共轴性,有利于光谱仪的紧凑化和批量化生产、装调。该方法具有普适性,对不同狭缝长度、不同光栅常数的共轴PGP 成像光谱仪均能快速给出合适的组合参数。但是本文未能进行弯曲狭缝成像光谱仪的实际成像实验,在之后的研究中若能进行相关的成像和光谱反演实验,则能够对弯曲狭缝PGP 成像光谱仪的性能有更清晰的认识。
——多功能光谱仪

