双目立体视觉成像系统水下建模与标定方法

刘建业，庄苏锋，屠大维，张璨，金攀

（上海大学 机电工程与自动化学院，上海 200072）

0 引言

双目立体成像技术在水下考古、海洋地质勘测、水下机器人自主导航和水下生物调查等领域具有广阔的应用前景［1，4］。然而，当相机应用于水下环境时，成像光线依次经过水、窗口玻璃和空气时会发生折射，使传统的小孔成像相机模型不再满足测量精度要求［5］。

早期的研究没有从水下光线的传播出发建立模型，而是采用简化的计算模型加以补偿［6-7］。例如，PARVATHI VS 等［8］提出补偿折射误差的标定模型，基于标定模型对基本矩阵进行估计，使用标准运动结构（Structure From Motion，SFM）算法进行对比度增强图像的三维重建，改善了三维重建的结果。后又提出了一种基于运动算法的单层折射方法［9］，证明了在姿态估计中使用折射运动结构（Refractive Structure From Motion，RSFM）优于SFM 算法，使三维重建结果有所提高。ELNASHEF B 等［10］提出了当系统和相机的光轴不重合时对水下标定模型的影响，但没有给出有效的办法。此后，研究者开始从光线传播的角度，关注水下物体成像的折射模型。例如，KOWN Y H 等［11］分析了折射效应对水下相机标定的影响，明确指出建立正确的折射模型是解决折射效应的基本方法。WEI Jingyang［12］对光线进入相机的路径进行分析，结合折射定律建立了水下成像模型，并改进了一种基于平面标定板的水下相机标定方法，提高了水下标定的精度，缺点是对物体大角度偏转区域的重建结果不太理想。LUCZYNSKI 等［13］提出了一种将虚拟针孔相机模型与轴向相机模型相结合的七轴相机模型，基于Pinax 模型补偿折射的图像失真，在水下三维重建中具有高效性，但这种方法的缺点是需要事先通过查找表进行折射校正。SUN J 等［14］提出了一种基于两条正交平行线消失点优化的快速水下标定方法，该方法操作简单，减少了水下标定现场的限制要求。LI S Q 等［15］提出了一种基于等效焦距的标定方法，将折射畸变视为等效焦距变化而引起，提高了水下相机的标定精度。KANG L 等［16］在不使用标定板或特殊设备的情况下解决了系统标定和三维场景重建等问题。上述方法解决了水下环境光照不足的问题，获得了较高的相机内外参数，但标定过程过于繁琐，导致计算量大和效率低。

建立一种精确的水下折射成像模型是提高双目立体测量系统标定精度的关键。为此，本文提出了一种基于光线四维参数化表示的水下双目立体视觉成像模型，提出系统参数标定方法，并构建最优目标函数进行非线性优化，最大限度地减小重投影误差以获取高精度的标定参数，从而提高水下三维测量的精度。

1 水下双目立体视觉成像模型

相机水下应用，被封装于防水密封舱体中，舱体前端具有玻璃窗口，光线的传播依次经过“水-玻璃-空气”三种介质，并最终在相机像平面成像。光线在不同介质的分界面处发生折射，使得水下相机成像的物像关系不满足空气中小孔成像原理。考虑到窗口玻璃厚度较小且两面平行，其折射影响可忽略不计，故简化的光路如图1。水下物点(xwor，ywor，zwor)的成像光线经过折射平面上一点(xref，yref，zref)，发生折射后在像平面的坐标为(u，v)，其中入射光线和折射光线与分界面法向量之间的夹角分别为θw和θa，f为相机焦距，d为折射平面到相机镜头中心的距离。

所有成像光线中任一条光线可用两个平面、四维参数表示［17］（如图2）：一个平面表示光的位置（[u ν]T），另一个平面表示光线的方向（[s t]T），两个平面的距离为1 个单位长度。因此，光线在空间上可表示为[u v s t]T。

图2 光线四维参数化表达Fig.2 Four-dimensional parametric expression of light

将相机坐标系建立在相机光心上，z轴与光轴平行（如图3 中的黑色坐标系）；以多层界面法线n为z轴，其与相机z轴的叉乘为x轴，构成多层折射成像坐标系（如图3 中的红色坐标系）。多层折射成像坐标系（ref）与相机坐标系（cam）间的关系为

图3 水下相机折射成像模型Fig.3 Refraction imaging model of underwater camera

式中，camRref、camtref为多层折射成像坐标系相对于相机坐标系的姿态，n为分界面法向量，zcam为相机坐标系的z轴。

物点坐标系（obj）相对于多层折射坐标系的关系为

式中，refRobj和reftobj为物点坐标系相对于相机坐标系的姿态。

在相机坐标系中建立物点P=[X，Y，Z]T与成像点m=[u，v]T之间的关系：=K·P，K为内参矩阵。假设像面平行于接口，任意像素m决定有一束光线通过光心和该像素。因此，在相机坐标系中，光的方向可表示为

即当光线Lref传输距离d0，从介质μ0折射到介质μ2，入射光和折射光分别表示为

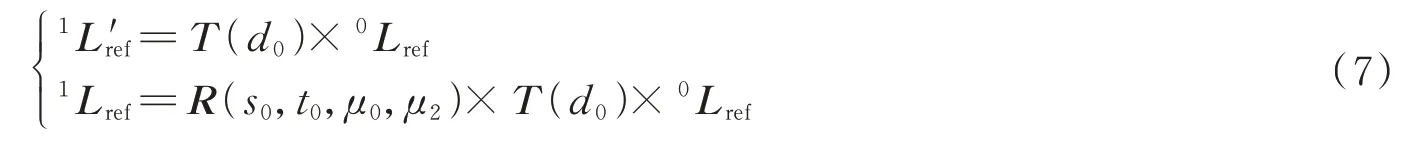
对于双目立体成像系统，以左相机光心为原点，左相机光心与右相机光心的连线方向为左立体视觉坐标系的x轴；将左平面折射坐标系的z轴（分界面的法线）与左立体视觉坐标系x轴的叉乘作为左立体视觉坐标系y轴；x轴与y轴叉乘作为z轴。将左立体视觉坐标系平移到右相机光心，即可得到右立体视觉坐标系。立体视觉坐标系与多层折射坐标系的关系可表示为

式中，refRste与reftste为立体视觉坐标系相对于多层折射坐标系的位姿，nx为左右相机光心连线，nref为分界面法向量。

建立的水下双目立体视觉模型如图4。

由于在左相机多层折射坐标系下点P同时位于右相机多层折射坐标系下（如图4），因此满足下列约束：

图4 水下双目立体视觉模型Fig.4 Underwater binocular stereo vision model

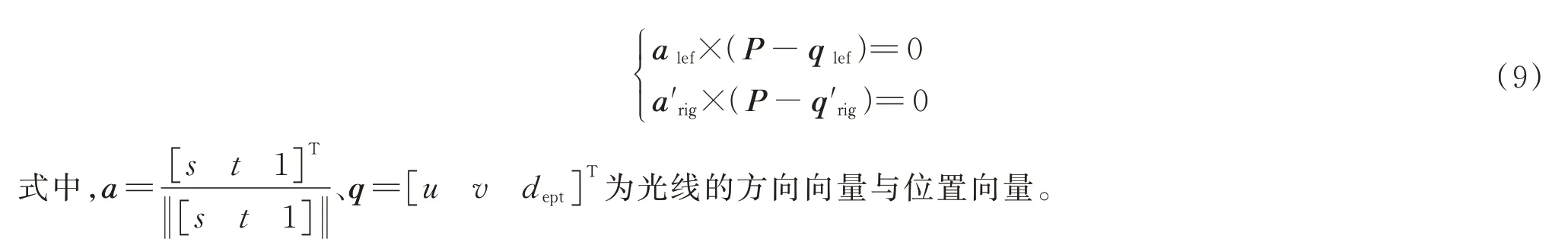
再用反对称矩阵表示代替叉乘（即向量积），式（9）可转化为

2 系统参数标定方法与仿真分析

2.1 系统参数标定

单相机内参及双目立体视觉系统外参可通过张正友标定法标定得到［18］。然而，对于图4 的水下双目立体视觉成像模型，由于制造和安装误差，相机光轴不可能垂直于分界面，需要通过标定确定分界面法向量n［19］。此外，相机被封装在密封舱内，空气介质厚度d0也是一个需要标定的参数。

2.1.1 分界面法向量标定

多层平面界面的成像系统具有共面特性，即入射光线与中间的传播光线和最终的折射光线共面。为了建模方便，多层平面之间当作平行处理，光路位于由入射光线和分界面法向量n确定的平面上。基于共面约束，可以计算出分界面法向量。

在相机坐标系中，相机光心为坐标系原点。对于任一物点Pobj经过多层界面后，它都位于入射光Icam与分界面法向量n确定的平面上，用⊗表示卷积运算。因此，可以将共面约束表示为

物点坐标系相对摄像机坐标系的姿态为camRobj、camtobj，物点Pobj坐标转化到相机坐标系的坐标可表示为Pcam=camRobjPobj+camtobj。将点Pcam的变换代入式（11）中，共面约束可以写为

将矩阵E按列向量形式保存在向量E(：)中，用⊙表示kronecher 积，式（12）可表示为

当物点坐标系中有11 个以上的已知点时，利用最小二乘法求得［17］。设物点坐标系中存在N个已知点，方程组可表示为

对B进行奇异值分解B=UΣVT，解是最小特征值对应的列向量V的最后一列。因此，V(：，12)，由此可得E。又因为E=n⊗camRobj，所以nTE=0，对E进行奇异值分解，可解出分界面法向量n的初值。

2.1.2 空气介质厚度标定

根据建立的折射模型知，只有已知分界面法向量的情况下，才能计算出空气介质厚度。2.1.1 节已标定出分界面法向量n，本节对空气介质厚度d0进行标定。

由光线经过折射的传播路径L'=R(s，t，μ，μ')⊗L知，折射光线方向只与入射光线的方向、界面法线、两个介质的折射率有关，与光线的位置无关。因此，光线可表示为

当第N层折射光线到达一定深度dn后，可以表示为

根据式（2）物点坐标系与多层折射坐标系之间的变化，式（17）可表示为

由N个点的约束方程不难发现，所有点的[d0…dn-1dn]T保持不变，唯独dn随物点变化而变化。在物点坐标系下，对于K个已知点可建立2K个约束方程，方程组可表示为

本文采用双层折射（玻璃厚度忽略），且μ0≠μ2，第二层的折射光线与第一层的入射光线不是平行的，根据式（19）可求得d0。

2.1.3 非线性优化分析

在标定得到分界面法向量n、空气介质厚度d0的初始值基础上，对其进一步优化，以获得更加精确的参数。由于反向投影误差的计算较为复杂，本文采用正向投射误差作为目标函数对参数n和d0进行优化，正向投射误差具体为：对于平面的标定物，将对应性的像素使用坐标变换可得在物体坐标系下的点坐标，两者相减作为正向投射误差。正向投影误差的代价函数表示为

式中，ϕ(pi，n，di，R，t)为正向投影函数，Pi为物点，pi为对应的图像点。

令每一段光路的方向向量为v0、v1，…，vn，相应的折射点为q1、q2，…，qn（如图5），因此vn可表示为

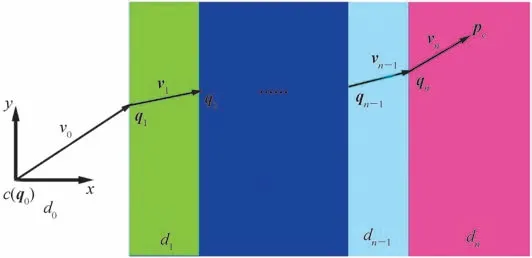
图5 多层折射光路示意Fig.5 Schematic of multi-layer refraction light path

将Pc向量分解为平行于x轴和平行于y的分量：

当有N对物点与成像点时，根据式（24）最优目标函数可表示为

因此，求解参数的过程是非线性优化过程，即

且在优化时需要使用多幅图片以降低图片质量对优化结果的影响。

2.2 仿真分析

根据2.1 节所述的多层折射参数标定理论进行分界面法向量n和空气介质厚度d0标定仿真实验，并利用标定的参数计算三维测量误差，以分析多层折射参数标定算法的正确性。

为反映真实情况，将标定板放置在1 500～2 500 mm 之间（标定板不与相机成像平面平行），在不同位姿共取样16 次，并提取角点信息，并在角点信息中加入均值为0、标准差σ为1 的高斯分布的背景光。首先根据其中1 幅标定板图片的角点信息计算待优化参数的初值，然后利用其中12 幅标定板图片进行正向投影误差非线性优化，并计算另外4 幅标定板图片中角点的反向投影误差，以测试标定结果的精度。仿真计算的结果以及真实系统参数如表1，其中n为分界面法向量，d0为空气介质厚度。当使用所提出的标定方法进行参数仿真标定后，平均重投影误差为0.078 pixel，表明标定算法的精度较高。

表1 仿真标定结果Table 1 Simulation calibration results

为分析背景光对标定精度的影响，对提取的角点数据分别加入均值为0、标准差σ为0 到1 的高斯分布的背景光，重复进行仿真标定，不同背景光下标定的平均重投影误差如图6。背景光对于标定结果的影响非常明显，因此在实际标定时，应尽量降低背景光的影响。

图6 不同背景光下的标定结果Fig.6 Calibration results under different background light

为进一步验证标定算法的有效性，根据标定参数进行三维计算精度仿真实验。首先，构建水下立体视觉系统，假定双相机的多层折射参数相同（如表1），取立体视觉系统的外参数为：R=[ 0 0 0 ]T，T=[-1200 0 0 ]T。然后，给定11×11 个空间三维点坐标（空间点均匀分布在3 m 远2 m×2 m 的平面），如图7，并计算出对应左、右相机像素理论坐标。最后，对理论像素坐标加入均值为0、标准差σ为1 的高斯分布的背景光，利用加入背景光的像素点根据第1 节介绍的水下多层折射三维数学模型计算物点的三维坐标。比较计算值与实际值，三维点X、Y、Z误差分布如图8。

图7 仿真模型Fig.7 Simulation model

图8 三维点X、Y、Z 误差分布Fig.8 X，Y，Z error distribution of three dimensional points

由仿真结果可知，采用提出的多层折射三维计算模型和标定算法时，三维点最大误差为1.395 mm，误差的标准差为0.437 mm，具有很高的精度。

3 实验与分析

3.1 实验装置与环境

软件环境为Win10+VS2015，算法编码采用C++。实验使用PointGrey 生产的GS3-U3-32S4C-C 相机，搭配Kowa LM5JC10M 的镜头。焦距为5 mm，相机分辨率为2 048×1 536。实验水池尺寸为3.5 m×2 m×0.9 m，水池内装满自来水（如图9）。

图9 实验环境Fig.9 Experimental environment

3.2 系统标定实验

标定实验分为空气和水下标定，在空气中主要标定相机内参、畸变系数和左、右相机的相对位姿，在水环境中主要标定左、右相机空气介质厚度和左、右分界面的法向量以及多层折射成像坐标系相对于相机坐标系的位姿。空气环境中的标定使用是14×11 的圆环标定板。对于水下参数标定，由于水折射率的影响，水下成像畸变较大，会导致拍摄的圆环标定板出现严重变形，从而无法精确提取圆环中心像素坐标。因此使用14×11 棋盘格标定板进行水下参数标定。

3.2.1 空气中标定

运用迭代标定算法进行空气中标定，标定场景如图10。具体标定结果如表2。其中，fx，fy为焦距，cx，cy为主点坐标，k1，k2，k3，p1，p2为畸变系数，Ra为右相机坐标系相对于左摄像机坐标系的旋转矩阵，Ta为相对应的平移向量。

表2 相机空气中的标定参数Table 2 Calibration paraments in camera air

图10 空气中标定场景Fig.10 Calibration scene in air

3.2.2 水下标定

在空气中标定参数的基础上，将折射率设置为1.333，进行水下标定，得到左、右相机空气介质厚度和左、右分界面的法向量以及多层折射成像坐标系相对于相机坐标系的位姿，场景如图11。标定时，需在1.5 m、2.0 m 和2.5 m 处分别拍摄6 组不同位姿的图片，使用其中12 组成像质量较好的图片进行标定。图12为水下标定时左右相机采集的标定板图片。表3 为水下标定参数，其中n为分界面法向量，d0为空气介质厚度，Rw为多层折射成像坐标系相对于相机坐标系的旋转矩阵，Tw为相对应的平移向量。

图11 水下标定场景Fig.11 Underwater calibration scene

图12 水下标定拍摄的一组图片Fig.12 A set of images taken by underwater calibration

表3 水下标定参数Table 3 Underwater calibration parameter

选择另外4 组图片标定结果进行测试，通过计算测试图中角点的重投影误差分析水下参数标定精度。测试图像的重投影误差如图13，重投影误差均在0.12 pixel 以下。可见，标定的系统参数具有较高精度。

图13 不同测试图片的重投影误差Fig.13 Reprojection error of different test images

3.3 水下精度实验

实验环境示意如图11。被测目标物为标准球棒（球径d1=d2=150.13 mm，球心距dis=497.72 mm，由上海计量院预先标定测得）。球棒置于水下双目相机前约3 m，并先后摆放10 个不同位姿（如图14）进行测量。基于以上模型和方法计算得到三维点云，再使用Ployworks 软件对球棒点云拟合，并将重建球径和球心距与标定真值进行比较，得到球径d1、d2与球心距dis的测量误差的标准差（Standard Deviation，SD）值，结果如表4。由表4 可知，对于水下球棒的10 个位置，d1的测量误差最大值为1.8 mm，其标准差为0.8 mm；d2的测量误差最大值为1.1 mm，其标准差为0.6 mm；dis 的测量误差最大值为1.8 mm，其标准差为 1.2 mm。因此，在10 种不同姿态下对球棒进行三维测量，得到球径d1测量误差的标准差为0.8 mm，球径d2测量误差的标准差为0.6 mm，球心距dis 测量误差的标准差为1.2 mm，充分说明基于标定算法的三维测量模型有较高的精度。

图14 球棒的10 个位姿示意图Fig.14 Diagram of the 10 positions of the bat

表4 10 种姿态下球棒的测量结果（单位：mm）Table 4 Measurement results of bat under 10 postures（unit：mm）

3.4 水下实物三维重建实验

实验对象为鲷鱼、大海螺，水下测量距离为2.1 m。图15（a）、（b）为左、右水下相机采集的一组图像。实验测得的点云数据如图15（c）。图中可见点云整体较稠密，无明显孔洞，而且轮廓良好且平滑，细节重建效果也很好，表明本文所提模型与标定算法的有效性。

图15 实验结果示意Fig.15 Schematic of experimental results

4 结论

针对空气中双目立体成像系统水下应用模型失效的问题，提出一种水下双目立体视觉成像模型，并据此开展标定方法研究。仿真分析与标定实验表明提出的水下双目立体视觉成像系统标定方法具有较高的系统参数标定精度，为之后的像素匹配与三维重建奠定基础；水下精度实验得到水下标准球棒d1测量误差的标准差为0.8 mm，d2测量误差的标准差为0.6 mm，球心距dis测量误差的标准差为1.2 mm，表明基于标定算法的三维测量精度很高。水下实物三维重建实验表明，提出的水下立体视觉模型和标定方法具有较好的水下三维重建效果。