Tunable triangular and honeycomb plasma structures in dielectric barrier discharge with mesh-liquid electrodes

Weili FAN (范伟丽), Xiaohan HOU (侯笑含), Miao TIAN (田淼),Kuangya GAO (高匡雅), Yafeng HE (贺亚峰), Yaxian YANG (杨亚贤),Qian LIU (刘倩), Jingfeng YAO (姚静锋), Fucheng LIU (刘富成),∗and Chengxun YUAN (袁承勋),∗

1 College of Physics Science and Technology, Hebei University, Baoding 071002, People’s Republic of China

2 Department of Physics, Harbin Institute of Technology, Harbin 150001, People’s Republic of China

Abstract We demonstrate a method to generate tunable triangular and honeycomb plasma structures via dielectric barrier discharge with uniquely designed mesh-liquid electrodes.A rapid reconfiguration between the triangular lattice and honeycomb lattice has been realized.Novel structures comprised of triangular plasma elements have been observed and a robust angular reorientation of the triangular plasma elements withθ π= 3 is suggested.An active control on the geometrical shape, size and angular orientation of the plasma elements has been achieved.Moreover,the formation mechanism of different plasma structures is studied by spatial-temporal resolved measurements using a high-speed camera.The photonic band diagrams of the plasma structures are calculated by use of finite element method and two large omnidirectional band gaps have been obtained for honeycomb lattices, demonstrating that such plasma structures can be potentially used as plasma photonic crystals to manipulate the propagation of microwaves.The results may offer new strategies for engineering the band gaps and provide enlightenments on designing new types of 2D and possibly 3D metamaterials in other fields.

Keywords: dielectric barrier discharge, triangular lattice, honeycomb lattice, photonic band diagrams, plasma photonic crystals

1.Introduction

Plasma photonic crystal (PPC) was first proposed by Hojo and Mase as a spatially periodic structure composed of alternating plasma and dielectric materials [1].It is a typical metamaterial that exhibits properties different from a homogeneous bulk plasma.In comparison to conventional photonic crystals (PCs), the use of plasmas brings about many promising features for PPCs due to its dispersive properties,tunable permittivity in both positive and negative regimes and active switching capabilities [2].The tunability of PPCs can also be performed at relatively high rates limited by the ionization or recombination times of the plasmas.These tunable responses give rise to various potential applications,such as the high-speed switch, microwave filter, path-reconfigurable circulator,highly sensitive sensor and plasma stealth aircraft [3–6].

In the past decade, significant efforts have been made to study PPCs motivated by its strong dispersion and dynamical controllability.In experiments, two types of PPCs are generally realized so far [7–20].The first type is formed by inserting solid rods or slabs into the uniform plasma background.Chaudhari et al proposed plasma metallic PCs consisting of an array of metal rods placed into the plasma background [7].Yao et al realized one-dimensional PPC by inserting an array of slab dielectrics into a glow discharge plasma [8].The second type consists of plasma rods that are arranged into a lattice that is placed in air or solid background.Such PPCs are normally fabricated by arranging gas discharges tubes into various arrays [9–13].Recently,microplasmas have proven to be a good candidate for the fabrication of dynamical and tailorable PPCs.It provides opportunities for the realization of high frequency band gaps and enables fast reconstruction between different structural configurations.Sakai et al proposed a square microplasma array in an atmospheric gas discharge and observed a unidirectional photonic band gap in T −X direction[14].Matlis et al achieved various triangular PPCs composed of selforganized plasma filaments in dielectric barrier discharge(DBD) and realized manipulation of electromagnetic (EM)waves in millimeter wavelength range[15].Lee et al obtained a square microplasma structure in DBD [16].Yang et al produced an array of microplasma jets by use of a dielectric barrier structure and realized attenuation of the microwaves at 157 GHz [17].Sun et al proposed a new type of 3D PPCs fabricated by embedding multiple plasma microcolumns into a metal/dielectric/polymer scaffold [18].In these works, the PPCs are generally composed of cylindrical plasma columns which are the basic units called plasma scatter elements.By varying the lattice constant, plasma density, angular orientation or number of the plasma scatter elements, the PPCs can be tuned dynamically.For instance,the plasma density can be tuned by changing the current of discharges [19].One can selectively turn on or off certain rows of plasma columns to control the lattice constant of plasma crystals[20]or rotate the whole PPCs mechanically to change the angular orientation.Nevertheless, the PPCs’ structural configurations, such as the spatial symmetry of the crystal, the shape and size of the plasma scatter elements, are normally immutable once the structures have been fabricated.These geometric parameters are of particular importance from the application perspective as they influence greatly on the positions and widths of the band gaps.How to realize a rapid reconstruction between different symmetries of plasma structures and furthermore achieve an effective control on the fine structures including the shape and size of the plasma scatter elements remains a significant challenge.In particular,it is interesting to produce new types of PPCs comprised of triangular plasma elements,which may have wide photonic bands and more exploitable properties as the PC counterparts with triangular scattering elements[21].Moreover,it is also desired to realize an active tunability on the angular orientation of the plasma scatter elements, while keeping the plasma structure static in operation.This will lead to an additional degree of geometric freedom in the dispersion engineering and bring about more promising properties for PPCs.

In this work, we propose an effective approach for realization of tunable triangular and honeycomb plasma structures via DBD with uniquely designed mesh-liquid electrodes.A rapid reconfiguration between the triangular lattice and honeycomb lattice has been realized.Novel plasma structures comprised of triangular plasma elements are demonstrated for the first time to our best knowledge.A robust angular reorientation of the triangular plasma elements withθ π= 3 is achieved.A dynamical control on the geometrical shape, size and angular orientation of the plasma elements has been realized.Moreover, the formation mechanisms of different plasma structures are studied by spatial-temporal resolved measurements using a high speed camera.The changes of photonic band diagrams with reconfiguration of different plasma lattices are also illustrated.The results reveal the formation mechanism of different plasma structures and explain the intriguing dynamical behaviors of the discharges.Such plasma structures can be potentially used as PPCs to control the propagation of microwaves of different frequencies.

2.Experimental setup

The DBD experimental set-up with mesh-liquid electrodes is presented in figures 1(a)and(b).The liquid electrode is made by use of a cylindrical container with diameter of 6.5 mm,which is sealed with 1.5 mm thick glass plates and filled with water.The conductivity of water is186.7μS.cm−1.The water serves as a coolant and transparent medium, allowing for observation and measurement of the plasma filaments[19].A metallic ring is immersed in the container and connected to the ground.The left is a mesh electrode which is connected to the sinusoidal alternating-current (AC) power supply.A ×10 cm 10 cm metal mesh composed of hexagonal cells is covered with a 1.5 mm thick quartz glass layer.The lattice constant which is defined as the distance between the centers of two adjacent hexagonal cells =a6.35 mm.The side length of the hexagonal cell =L4 mm.A square glass frame with thickness of 1.5 mm is placed between two parallel glass plates, serving as the discharge spacer.The whole cell is placed in a big chamber,whose gas pressure and gas composition can be adjusted.A camera(Canon EOS 6D)is used to record the time-averaged images of plasma structures.The voltage and current waveforms are detected by high-voltage probe (Tektronix P6015A 1000×) and current probe(Tektronix TCP0030A),respectively,and recorded by a digital phosphor oscilloscope (Tektronix TDS3054B).The discharge power P can be estimated by calculating the area enclosed by the charge–voltage ( −Q V) curve, which is a parallelogram in Lissajous figure [22, 23].An intensified charge-coupled device camera (ICCD: Andor DH334T) is utilized to record frames from the end view of the liquid electrodes.A trigger is utilized to synchronize the discharge current waveform and ICCD camera in experiments.The exposure time Δt and the loop times N of ICCD can be controlled by a software to capture the instantaneous images.

Figure 1(c) presents the distribution of Laplacian potential along the surface of the mesh electrode without formation of plasmas.It is calculated by use of COMSOL Multiphysics software.One can see that the spatial distribution of Laplacian potential matches well with the geometry of mesh electrode.Namely, the mesh electrode introduces a two-dimensional spatial periodic potential to the gas gap,which determines the lattice constant and the symmetry of the plasma structures.One also notes that the electric potentials at the six vertexes of the hexagonal cell are remarkably higher than the other regions, giving preference to formation of the discharges.These regions have a regular triangular shape, leading to the triangular shape of the plasma elements as will be demonstrated below.

3.Results and discussion

Figure 2 presents structural reconfiguration from the triangular lattice to honeycomb lattice with increasing of the supply voltage.These plasma structures not only can be controlled in their spatial symmetries, but also allow for active modulation in time.As shown in figure 2(a),when the discharge is just ignited at low voltage =U3.0 kV, a welldefined triangular lattice is produced, which is composed of triangular plasma spots located at the three vertexes of the hexagonal cell (figures 2(c) and (e)).Only a single current pulse appears in per half period of the supply voltage within a time window aboutμ0.2 s.It repeats in the same manner in each subsequent half-period with the jitter less than 0.1 ms(figure 2(g)), suggesting that the discharge has rather good temporal periodicity determined by the frequency of the AC voltage.By adjusting the frequency of the supply voltage,the generation of triangular lattice can be controlled temporally.With rising of the supply voltage to =U3.4 kV,an intriguing honeycomb lattice is produced as shown in figure 2(b).The plasma spots emerge at the six vertexes of the hexagon cell of the mesh electrode and their shapes turn to be circular(figures 2(d) and (f)).Similar to that of the triangular lattice,only a single current pulse appears in per half period of the voltage within a time window aboutμ0.15 s (figure 2(h)).Both of the triangular and honeycomb lattices are highly stable, in which the position and the shape or size of plasma elements are fixed,unless the discharge parameters have been changed.Moreover, the transformation between these two plasma lattices is reversible and can be completed very fast,taking only several seconds.Consequently, a rapid reconfiguration between the triangular lattice and honeycomb lattice has been realized here.These two types of plasma lattices have both good spatial and temporal symmetries, which can be controlled by the amplitude and frequency of the supply voltage,respectively.The mesh electrode and the electric field geometry are the key factors to realize these plasma structures.The discharges tend to occur at the six vertexes of the hexagonal cell of the mesh electrode, where the Laplacian potentials are large,as shown in figure 1(c).The fundamental symmetry and the lattice constant of the plasma structures are well consistent with the mesh electrode.If the configuration of mesh electrode has been changed, the plasma structures will be changed correspondingly.From the viewpoint of potential applications, different dispersion relations would be produced for these two plasma lattices owing to their different structural configurations, allowing for manipulation of the propagation of EM waves of different frequencies.

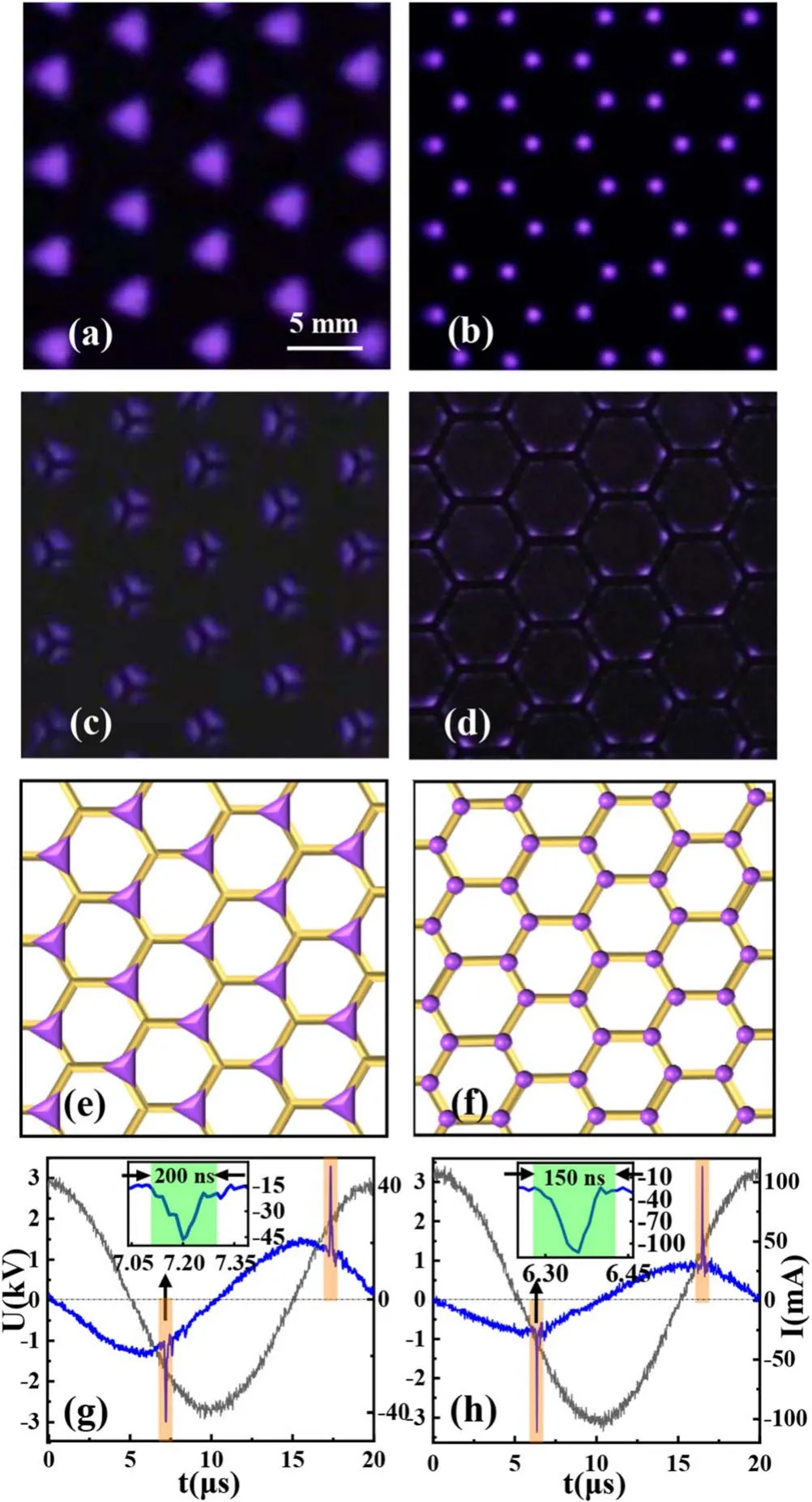
Figure 2.Triangular plasma lattice and honeycomb plasma lattice obtained by raising the supply voltage.(a), (b) Snapshots of triangular lattice and honeycomb lattice taken at the end of the transparent liquid electrodes.U =3.0 kV, P =1.9 W in (a) and U =3.4 kV, P =3.4 W in (b).The other discharge parameters are:the frequency of the AC voltage f =50 kHz, the gas gap d =1.5 mm, the mixture gas is composed of 60% Ar and 40% air,the gas pressure p =152 Torr, the exposure time Δt = 1 10 s.(c), (d) The end views and side views of triangular lattice and honeycomb lattice.(e), (f) Schematics of the distribution of the plasma spots on the hexagonal mesh.(g),(h)The oscillogram of the discharge current I (blue line) and the supply voltage U (black line)during one period of the supply voltage.The insets show closeups of the current pulses.The duration of the discharge pulse is marked by the green stripe in the inset.

Figure 3.Spatio-temporal resolved measurements for the triangular plasma lattice corresponding to figure 2(a).The figures(a)–(f)are the images of the plasma structures taken by a high speed camera with the exposure times Δt = 5 ns, 10 ns, 25 ns, 50 ns, 100 ns and 200 ns, respectively.

Figure 4.The time-integrated images of the triangular plasma lattice over multiple voltages cycles, corresponding to figure 2(a).The images are integrated for 1, 10, 25 and 50 voltage cycles,respectively,in(a)–(d)with the exposure time Δt = 200 ns.The red triangles in (c) and (d) denote the shape of the plasma elements.

In order to get an understanding on the formation mechanism of these novel structures, the spatial-temporal resolved measurements have been carried out by use of a high speed camera.Figure 3 shows the images of the triangular plasma lattice with the exposure time Δt = 5 ns,10 ns, 25 ns, 50 ns, 100 ns and200 ns, respectively.One can see that when the exposure times are small at Δt = 5 ns and 10 ns, only a few of random filaments are ignited(figures 3(a) and (b)).These filaments are thin with the diameter about 0.7 mm,which are much smaller than the size of the triangular plasma elements as one can see in the timeaveraged plasma structures (figure 2(a)).No regular plasma structures can be obtained in such small time scales.With increasing of the exposure time, more filaments can be observed and a hexagonal lattice structure can be identified with Δt = 50 ns as shown in figure 3(d).This structure becomes more and more obvious and the sizes of plasma spots are increased with further increasing of the exposure time (figures 3(e) and (f)).Figure 3(f) shows the triangular plasma structure with the exposure time Δt = 200 ns, which is approximately equal to the duration of the current pulse in per half period of AC voltage.One notes that the shape of the plasma elements is not triangular here as they appear in the time-averaged structure.In particular, if we examine the plasma elements carefully, it can be seen that each plasma element consists of one or two thin filaments.This implies that the large plasma elements result from the integration of several individual filaments.Although these filaments are not strictly synchronized, a well-defined triangular structure can be produced within the exposure time50 ns(figure 3(d)).The non-synchronization of the discharge filaments is reasonable and inevitable, which is attributed to the intrinsic stochastic property of the discharges such as the collision-ionization,secondary-electron emission, the asymmetry of two electrodes and the distribution of surface charges [24, 25].It is known that the surface charges have a‘memory effect’,which sets up a field opposite to the external field to extinguish the discharge while facilitating the next discharge at the same location.Since the surface charges are generally localized at the positions of filaments due to their slow mobility on the dielectrics, they result in a transversely nonuniform surface charge field [26–28].The net field imposed on the working gas,which is the combination of the surface charge field, the external field, and the space charge field is transversely nonuniform.The filaments will be ignited where the net field reaches the breakdown field threshold.The interplay between the surface charge field, the external field, and the space charge field gives rise to dynamical behaviors of the DBD filaments.To elucidate the formation mechanism of the triangular plasma elements, the time-integrated of discharge filaments over multiple discharge periods have been studied as shown in figure 4.One can see that the plasma elements are not triangular with one voltage cycle =N1(figure 4(a)) and one or two individual filaments can be identified in each plasma element as described previously in figure 3(f).With increasing of the number of the supply voltage cycles N for integration, the size of the plasma elements is increased and the shape turns to be triangular gradually.Similar results can be obtained when the inner part inside the red triangles in figure 4(d)has been resolved.Consequently,the formation of triangular plasma elements results from spatio-temporal integration of random filaments over multiple voltage cycles.These filaments distribute in the triangular area located at three vertexes of the hexagon cell of the mesh electrode,where the Laplacian potential is large as shown in figure 1(c).

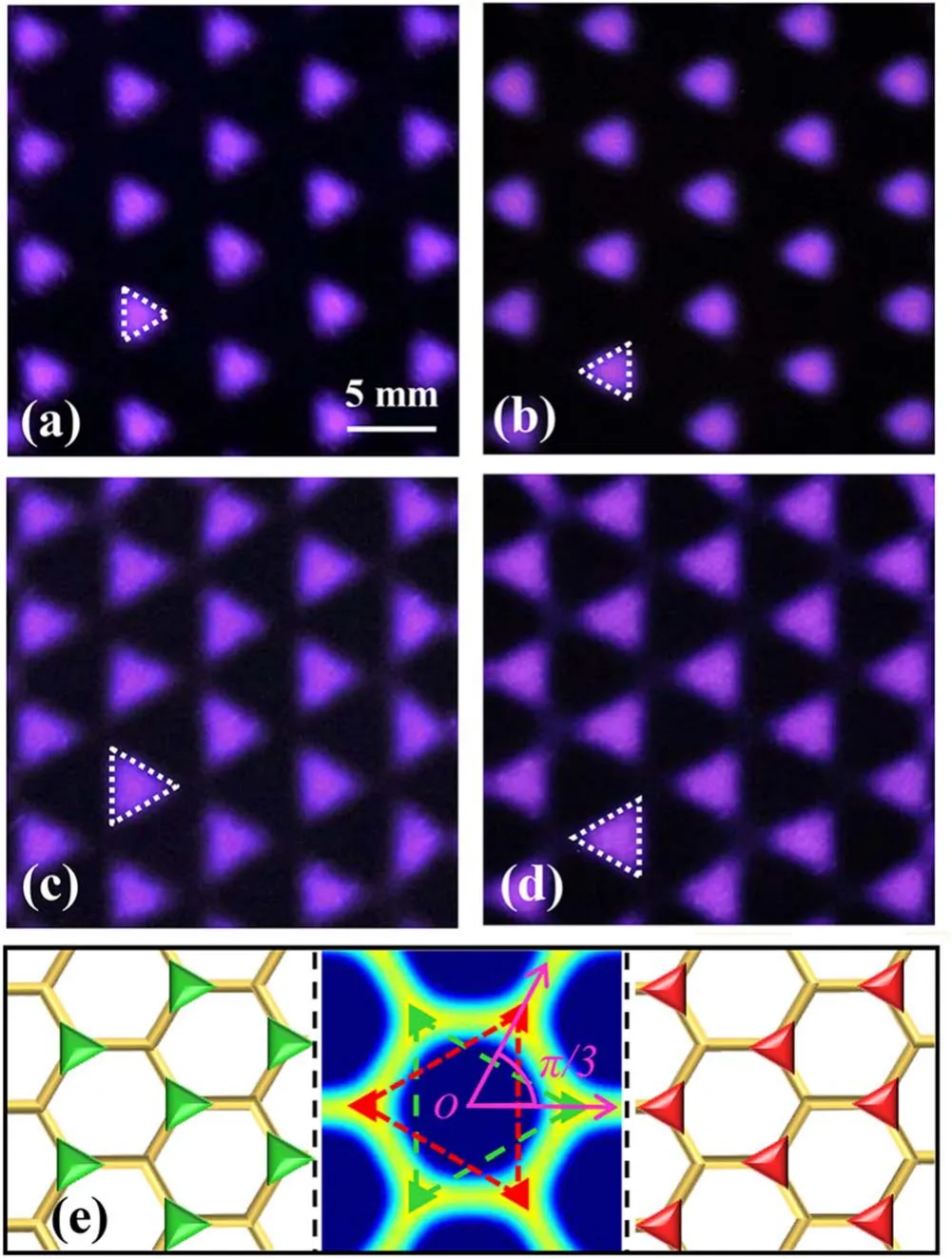
Figure 5.Various triangular lattices with different orientations of the triangular plasma elements.(a)–(d) Snapshots of the triangular lattices.(a) U =3.0 kV, P =1.7 W, p =190 Torr,the mixture gas is composed of 80% Ar and 20% air.(b) U =3.0 kV, P =2.9 W,p =380 Torr,the mixture gas is composed of 50%Ar and 50%air.(c) U =2.6 kV, P =1.9 W, p =190 Torr, the mixture gas is composed of 90% Ar and 10% air.(d) U =2.6 kV, P =1.7 W,p =152 Torr,the mixture gas is composed of 80%Ar and 20%air.The other discharge parameters are:the frequency of the AC voltage f =50 kHz, the gas gap d =1.5 mm, the exposure time Δt = 1 10 s.The white dashed triangles denote the unit cell of the plasma structure.(e) Schematic diagrams of the triangular lattices that have different orientations of the triangular plasma elements.The corresponding positions of these two different triangular lattices are marked in the Laplacian potential distribution diagram in the middle of figure (e) by green and red colors, respectively.The rotation angle between two triangular latticesθ = π3.

Remarkably, an active tunability on the angular orientation of the triangular plasma elements in triangular lattice is also realized in our experiments as shown in figure 5.One can see that at a fixed supply voltage =U3.0 kV (figures 5(a)and (b)), the orientation of triangular plasma elements changesπ3 by changing the gas pressure and compositions.However, the lattice constant, the symmetry of the plasma structures as well as the size of the plasma elements remain invariant during the angular reorientation.At a reduced voltage =U2.6 kV as shown in figures 5(c) and (d),triangular lattices composed of larger triangular elements have been obtained.Similarly, the orientation of triangular plasma elements changesπ3 when the gas pressure and compositions have been varied.One notes that a robust angular reorientation of plasma elements withθ π= 3 has been achieved, albeit under different discharge conditions.This can be well explained through the distribution of Laplacian potentials as illustrated in figures 1(c)and 5(e).The regions with high Laplacian potentials locate at the six vertexes of the hexagonal cell of the mesh electrode, whose shape is triangular.The discharges are prone to occur at these regions and the spatio-temporal integration of the filaments over multiple voltage cycles results in formation of the triangular plasma elements.Firstly, the triangular lattice with the plasma elements located at the positions marked by the green color in figure 5(e) is selected, corresponding to the triangular lattice shown in figures 5(a) and (c).When the discharge parameters have been changed,the triangular lattice with plasma elements located at the positions denoted by the red color in figure 5(e) is selected, corresponding to the triangular lattice shown in figures 5(b)and(d).This rule can be clearly identified from the different positions of plasma elements between figures 5(a) and (b), figures 5(c) and (d),respectively.These two triangular lattices are complementary,showing a constant rotation angleθ π= 3.It is known that the angular orientation of scatter elements is an important parameter that influences significantly on the transmission characteristics of the EM waves passing through a PC.The conventional method to adjust the orientation of scatters is by rotating the whole PCs mechanically.Recently, a theoretical study on the effects of orientation of scatters upon the complete photonic band gaps in two-dimensional dielectricplasma PCs has been carried out.An optimum angleθ= °15 is found to yield large band gaps for the triangular lattice with square plasma scatters [29].Here we present an intriguing phenomenon that the orientations of plasma scatters can be dynamically changed by readily changing the discharge parameters.A robust angular reorientation of the triangular plasma elements withθ π= 3 is suggested.This may offer new strategies for engineering the band gaps for PPCs and provide insights to design new types of tunable PCs in other fields.

It is interesting to note that both the geometric shape and the size of the plasma elements can be dynamically tuned in the honeycomb plasma lattice.Figure 6 presents the honeycomb lattice composed of circular plasma elements (HBC)withl1=1.5 mm (figures 6(a) and (d)), the honeycomb lattice composed of petaloid plasma elements (HBP) withl2=2.0 mm (figures 6(b)and(e)),and the honeycomb lattice composed of regular triangular plasma elements (HBT) withl3=2.4 mm (figures 6(c) and (f)), respectively.To our best knowledge, HBT is a new kind of plasma crystal structure that is obtained for the first time.One can see that the shape of the plasma elements distorts significantly from circular to regular triangular,meanwhile the sizes of plasma elements are profoundly increased with reducing of the gas pressure and the supply voltage.However, the lattice constant keepsa=6.35 mm and the symmetry remains invariant, which is determined by the geometry of the mesh electrode.To be specific, while the symmetry and the lattice constant of plasma structures are well preserved,the fine structures of the plasma elements (the geometric shape and the size) can be changed dynamically.To get knowledge of the formation mechanism of different honeycomb lattices, the spatio-temporal resolved measurements with different exposure times have also been carried out.Similar to the triangular lattice as described in figures 3 and 4, the formation of the plasma elements with different shapes results from the spatiotemporal integration of the discharge filaments over multiple voltage cycles.The filaments occur randomly in the triangular area located at six vertexes of the hexagon cell of the mesh electrode, where the Laplacian potential is large.

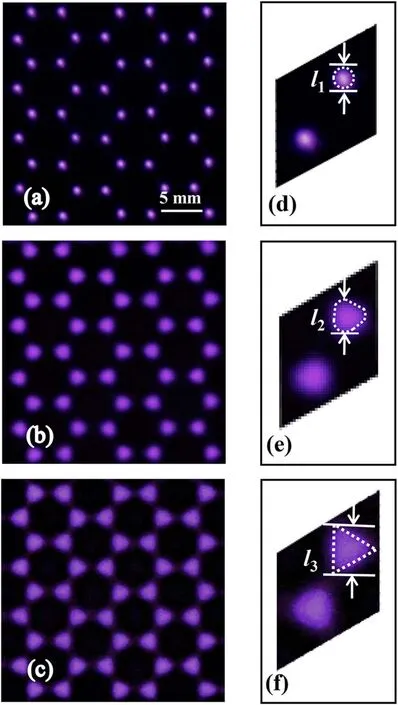
Figure 6.Honeycomb lattices composed of different shapes of plasma elements.(a) Honeycomb lattice composed of circular plasma elements, U =4.0 kV, P =3.5 W, p =190 Torr.(b) Honeycomb lattice composed of petaloid plasma elements,U =3.0 kV, P =1.7 W, p =114 Torr.(c) Honeycomb lattice composed of regular triangular elements, U =2.6 kV, P =1.4 W,p =76 Torr.The other discharge parameters are: the frequency of the AC voltage f =50 kHz,the mixture gas is composed of 30%Ar and 70% air, the gas gap d =1.5 mm, the exposure time Δt = 1/ 10 s.(d)–(f) The basic units of the honeycomb PPCs with circular, petaloid and triangular elements.

The triangular lattice and honeycomb lattice are two important candidates for the fabrication of PCs.They are not only easy to manufacture for customizable and large-scale production but also exhibit extraordinary optical properties and rich applications [30–37].The shape and size of the scatter elements have a great influence on the positions and widths of the band gaps [38].Large complete photonic band gaps can be obtained in a triangular PC with triangular air holes [21].The characteristics of topological edge states can be changed greatly by varying the shape of the scatter elements in a honeycomb PC [37].From the viewpoint of discharge plasmas, different PPCs comprised of cylindrical microplasma columns have been obtained in gas discharge systems [9–20].They have significant effects upon the transmittance of the microwaves, by varying the plasma density or the lattice constants of the structures, despite that the size and geometry of the plasma elements are normally immutable.If the frequency of the incident microwaves lies in the range of the band gaps, the microwaves can be reduced significantly.For instance,a transmittance reduction by 10%–20%was obtained by Sakai et al for square PPC[14].Matlis et al observed the reduction of S21transmittance by up to 75% at the band gap for triangular PPC [15].Although these PPCs may have complicated dynamical discharge behaviors,the band gaps can be successfully detected for the timeaveraged plasma structures [14–18].An average electron density in PPCs can also be estimated from the transmittance spectra of the EM waves passing through the microplasma structures.Based on these experimental results, we propose that the triangular and honeycomb plasma structures suggested here may potentially be used as PPCs which have band gaps to manipulate the propagation of microwaves.With reconfiguration of different plasma structures, the band diagrams will be changed significantly.Thus we will next study the band diagrams of different honeycombs lattices whose geometric shape and size of the plasma elements can both be actively tuned(figure 6).As the first step of research,we take no consideration on the complicated dynamical behaviors of the discharges and the dispersion relations of the time-averaged plasma structures have been investigated.The experimental diagnosis of the band gaps will be carried out in future and meanwhile a larger discharge gas gap will be adopted in further work to facilitate practical applications of PPCs.

The dispersion relations of different plasma honeycomb structures under the transverse-magnetic mode have been studied by use of the COMSOL software under the Lorentz–Drude model.Three-dimensional complex-value electric field in the form of

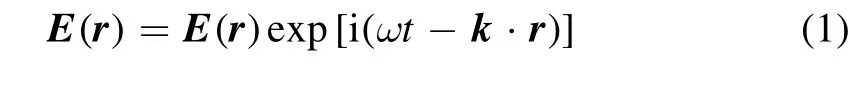
is considered,where ( )E ris the electric field at position r,k is wave vector andωis the angular frequency.From Maxwell’s equations,the propagation of electromagnetic waves in terms of the electric field can be expressed by the Helmholtz equation, written as

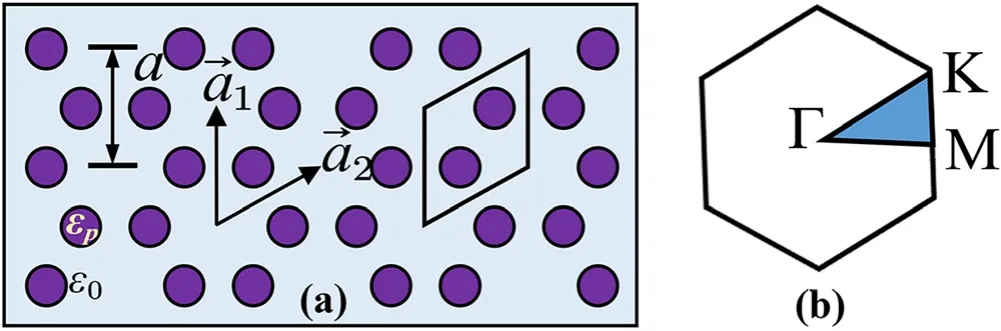
Figure 7.Schematics of a honeycomb lattice (a) and the corresponding reduced Brillouin zone (b).Here a¯1, a¯2 are the unit vectors,a is the lattice constant with a =6.35 mm,andε p,ε0 are the dielectric constants of the plasmas and the neutral gas.The enclosed parallelogram in (a) marks the basic unit of the honeycomb lattice.The triangular region in(b)indicates the irreducible Brillouin region with the boundary M −Γ − K −M.

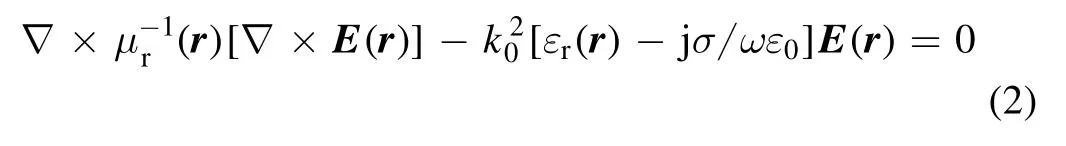
hereμr(r)andεr(r)are the permeability and the dielectric constant,respectively.The dielectric conductivit yσ= 0.The wave vectork0is given as

In the plasma regions,εr(r)is expressed asεpgiven as

whereωpeis the plasma frequency withωpe=(e2neε0m)12[39].neis the electron density,which is generally in an order of 1014cm−3to 1015cm−3under the experimental conditions we employed here [40, 41].We set an average electron densityne= 9.5 × 1014cm−3according to the spectrum measurement results in our previous study [40].For simplicity, we assume that the average electron densityneis invariant for different honeycomb lattices and only concentrate on the influences of the shape and size of plasmaelements on the bandgap structures.νm=Ngδc(υ)υis the electron collision frequency between electrons and atoms or molecules, whereυis the thermal electron velocity,Ngis the density of background gas atoms andδc(υ)is the collision cross section.The partial differential equation (2) can be converted to a weak form of an integral equation, which is solved by use of finite element method (FEM) in COMSOL software [42].The mesh division is selected as the free triangle meshes.The largest mesh element is1.9 ×10−4mand the smallest mesh element is less than one sixth of the incident wavelength.The curvature factor is set as 0.25.According to Bloch’s theorem, the eigen frequencies normalized by a constantωπac2 for each wave vector k along the irreducible Brillouin zone boundary (figure 7(b)) have been calculated, giving rise to the band diagrams.

Figure 8.Photonic band diagrams of different honeycomb structures.(a) The band diagram of HBC corresponding to figure 6(a) with νm = 335 GHz.(b) The band diagram of HBP corresponding to figure 6(b) withνm = 201 GHz.(c) The band diagram of HBT corresponding to figure 6(c) withνm = 134 GHz.The gray stripes denote the positions of the band gaps.

Figure 8 illustrates the band diagrams of HBC,HBP and HBT corresponding to the honeycomb plasma lattices shown in figure 6.One can see that two omnidirectional band gaps and a unidirectional band gap form for HBC,which locate in the ranges of−32 41 GHz,−55 56 GHz and−65 70 GHz in −K M direction, respectively (figure 8(a)).The widths of two omnidirectional band gaps are significantly increased when a HBP is produced, whereas the width of the unidirectional band gap in −K M direction is reduced.The two omnidirectional band gaps are in the ranges of −34 50 GHz and −58 66 GHz, respectively, and the unidirectional band gap locates in the range of −71 74 GHz (figure 8(b)).Remarkably, when the HBP changes to HBT, the widths of two omnidirectional band gaps have been further enhanced,which are in the ranges of−34 51 GHz and−57 68 GHz with the widths of Δ =f17 GHz and 11 GHz, respectively(figure 8(c)).However,the unidirectional band gap in −K M direction disappears in this case.The formation of wide omnidirectional band gaps for HBT is attributed to an increase of the filling fraction of plasmas as well as the changes of the geometrical shapes of plasma scatters.Since all the novel properties as well as the application of PCs rely on the existence of photonic band gaps, it is essential to design crystal structures with omnidirectional band gaps as large as possible.Here we propose a new type of honeycomb lattice with triangular plasma scatters, which possess large omnidirectional band gaps.The photonic band gaps can be substantially improved with reconstruction from HBC to HBT.This merit is beneficial to fabricating integrated and high-performance optical devices and provides additional tunability to PCs.

4.Conclusions

In summary, we have demonstrated experimentally the generation of tunable triangular and honeycomb plasma lattice structures via DBD with mesh-liquid electrodes.Novel plasma structures composed of triangular plasma elements have been obtained.Fast reconfiguration between the triangular lattice and honeycomb lattice is realized.We also enable to make an active control on the geometrical shape, size and orientation of plasma elements, while keeping the symmetry and the lattice constant of plasma lattice fixed.A robust angular reorientation (θ π= 3) of the triangular plasma elements in the triangular lattice has been achieved.The spatial-temporal resolved measurements for different plasma structures are studied by use of a high speed camera.It is shown that the formation of different shapes of plasma elements results from the spatio-temporal integration of random filaments over multiple voltage cycles.The random filaments occur in the regions with high Laplacian potentials, depending on the geometrical configuration of the mesh electrode.Moreover, the changes of the photonic band diagrams with reconfiguration of different honeycomb plasma structures have been calculated by use of FEM.Two large omnidirectional band gaps are obtained for the honeycomb lattices and the photonic band gaps are substantially improved with the reconstruction from HBC to HBT.We propose a variety of fascinating plasma lattice structures in DBD and reveal the underlying physics for the formation of these structures.The results may provide new vistas for engineering the band gaps for PPCs and find promising applications in the manipulation of microwaves.

Acknowledgments

This work was supported by National Natural Science Foundation of China (Nos.11875014, 11975089) and the Natural Science Foundation of Hebei Province (Nos.A2021201010, A2021201003, and A2017201099).

ORCID iDs