基于BPNN端到端时延预测的多路传输调度
苏旭东,衷璐洁
(首都师范大学 信息工程学院,北京 100048)
0 引 言
MPTCP(MultiPath TCP)是一种基于多接口的传输控制协议,允许在多条链路同时传输数据,旨在提高吞吐量的同时更充分地利用网络资源。在移动网络环境下,带宽、延迟、丢包率等网络参数动态变化,终端的移动性会引发网络链路间的频繁切换,造成数据包不能按序到达接收端,引起数据包乱序问题。乱序数据包在接收端缓冲区滞留等待,严重时会导致接收端缓存阻塞,造成网络延迟,降低网络吞吐量。在该问题背景下,如何针对移动异构网络特点,减少数据包乱序发生可能,实现高效移动多路传输调度具有重要意义。对此,本文提出一种基于BP神经网络(back propagation neural network,BPNN)端到端(传输)时延预测的移动多路传输调度方法,综合考虑链路丢包率、RTT、吞吐量等性能参数,通过BP神经网络的训练与学习,提取输入性能参数与端到端时延间的有效规则,在更准确预测端到端时延的基础上,对路径拥塞状况进行计算评估,并基于路径综合评估结果实施数据包调度,以使数据包尽可能按序到达接收端,进而有效避免缓冲区阻塞,实现负载均衡,提高多路传输网络吞吐量。
1 相关工作
MPTCP数据调度:Ke等[1]利用自定义的排序算法对路径状态信息进行排序,之后基于排序结果实现数据包的传输。黄辉等[2]提出一种将RTT与丢包率相结合,运用综合效用函数作为评估指标的数据调度机制。Luo等[3]提出一种基于强化学习DQN的数据调度算法,通过强化模型完成路径的选择判断,并借助路径奖惩值计算实现路径选择的更新。
基于端到端时延的调度:Xue等[4]通过计算在接收端不发生乱序的前提下应为每条路径分配的数据包个数,为各路径分配DSN连续的数据包。王振朝等[5]利用路径带宽、往返时延和拥塞窗口预测数据包到达时间,并以此为基础完成数据包的分发。Dong等[6]根据子流是否丢包对端到端时延采用不同的计算方法进行估算。Froemmgen等[7]通过主动探测未使用的子流并根据传统TCP时间戳选项得到的端到端时延来调度数据包。
数据包乱序减少:Han等[8]通过预测数据包到达时间,将数据包调度到最早到达时间的子流上,以保证数据包到达的顺序。Shi等[9]选择慢路径发送序列号较大的数据包。Kim等[10]通过估算无序数据包数量及传输所需的缓冲区大小来减少数据包乱序的发生可能。Ling等[11]对路径阻塞时延进行评估,选择不易造成阻塞的子流集进行数据传输。
2 基于BP神经网络端到端时延预测的多路传输调度
基于BP神经网络端到端时延预测的多路传输调度(multipath scheduling based on BP neural network EET prediction,MSBPEET)通过综合考虑丢包率、吞吐量、RTT等路径性能参数,构建BP神经网络对数据包在各路径上的端到端时延实施预测,随后选择时延小且拥塞状况良好的路径进行传输,以使数据包在尽可能短的时间内按顺序到达接收端。方法总体框架如图1所示,包括:(Ⅰ)RTT预测;(Ⅱ)基于BP神经网络的端到端时延预测;(Ⅲ)子流拥塞状况评估;(Ⅳ)网络状态综合评估及有效路径集排序调度4个部分。其中:RTT预测部分将RTT及RTT高频变化分别建模为常量信号和噪声,然后结合卡尔曼滤波,对当前RTT测量值进行评估和纠正;基于BP神经网络的端到端时延预测部分主要通过BP神经网络的构建、训练和学习完成对端到端时延的更准确预测;子流拥塞状况评估部分主要完成对各个子流的拥塞状况评估;网络状态综合评估及有效路径集排序调度部分主要负责在对路径完成综合评估后,选择最优路径进行数据包调度。
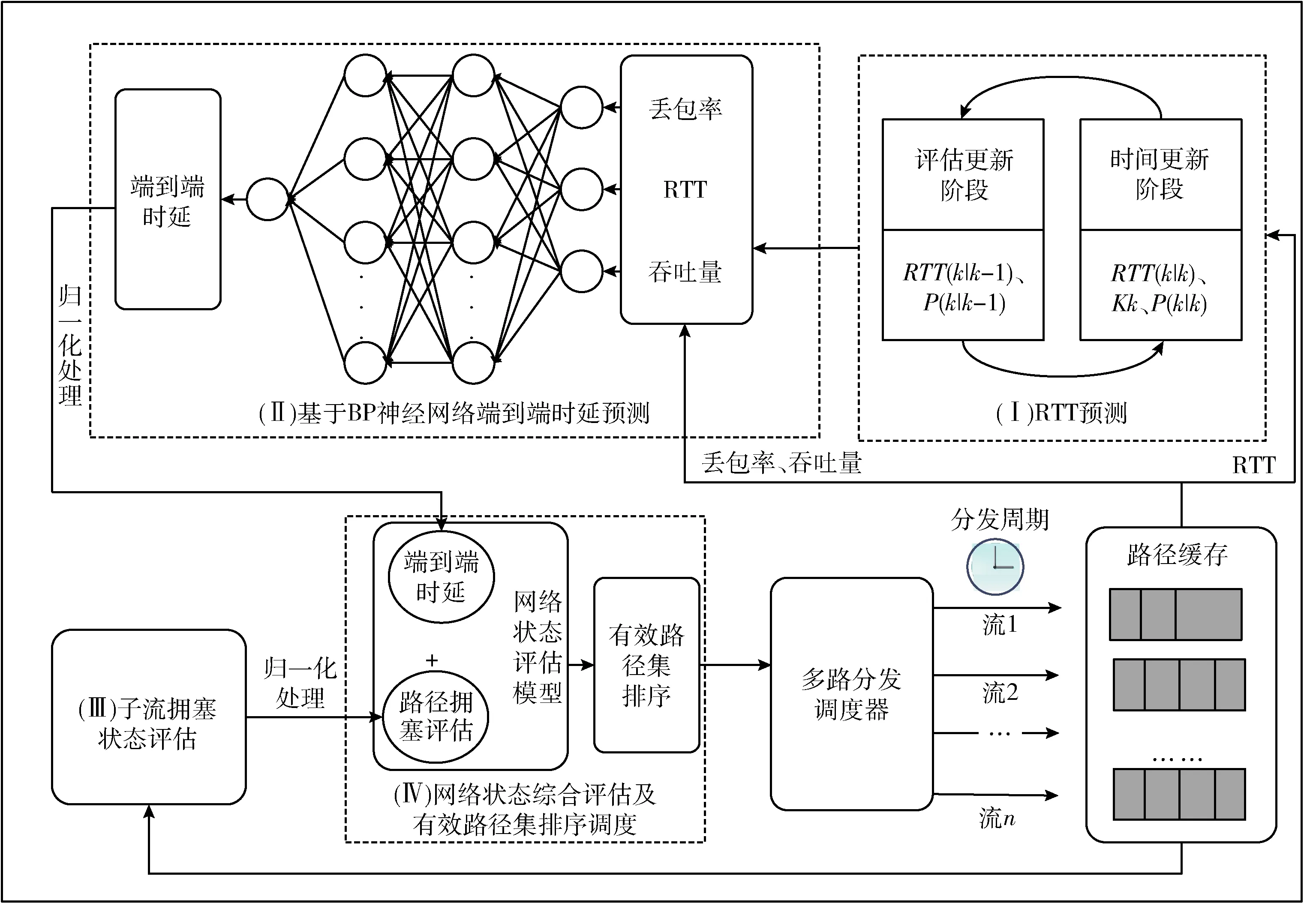
图1 基于BP神经网络端到端时延预测的多路传输调度
2.1 RTT预测
RTT是路径质量评估的重要参数。在本文中,RTT作为BP神经网络的输入,其预测准确性将直接影响端到端时延预测的准确性。在路径参数高度动态变化的移动无线网络环境下,为进一步提高RTT预测的准确性,本文采用卡尔曼滤波方法,利用前一时刻的RTT与当前时刻RTT的测量值来更新对RTT的预测估计,进而获得当前时刻RTT更准确的估计值。
首先将RTT及RTT高频变化分别建模为常量信号及噪声,如式(1)和式(2)所示
RTTk=RTTk-1+wk
(1)
RTT′k=RTTk+vk
(2)
其中,RTTk和RTTk-1分别表示当前时刻k和上一时刻k-1的RTT;wk表示过程噪声,服从高斯分布;RTT′k表示当前时刻RTT的测量值;vk是测量噪声,服从高斯分布。RTT卡尔曼滤波预测过程如下:
(1)初始化测量噪声R、 过程噪声Q和误差协方差P;
(2)对任一MPTCP子流j,若子流j收到ACK或发生超时,获取子流j当前时刻RTT测量值RTTk及上一时刻最优RTT估计值RTT(k-1|k-1)。 初次预测时,将子流j上一时刻的RTT测量值RTTk-1视作上一时刻的最优RTT估计值,然后转步骤(3)~步骤(7)。
时间更新阶段:
(3)计算当前时刻RTT的预测值,记作RTT(k|k-1), 如式(3)所示
RTT(k|k-1)=RTT(k-1|k-1)
(3)
(4)计算当前时刻误差协方差的预测值,记作P(k|k-1), 如式(4)所示
P(k|k-1)=P(k-1|k-1)+Q
(4)
其中,P(k-1|k-1) 为上一时刻误差估计协方差;Q为过程噪声,服从高斯分布。
评估更新阶段:
(5)根据当前时刻误差估计协方差更新卡尔曼增益Kk, 如式(5)所示
Kk=P(k|k-1)(P(k|k-1)+R)-1
(5)
其中,R为测量噪声,服从高斯分布。
(6)根据卡尔曼增益Kk和当前时刻RTT预测值RTT(k|k-1) 及当前时刻RTT测量值RTTk计算当前时刻最优RTT估计值,如式(6)所示
RTT(k|k)=RTT(k|k-1)+Kk(RTTk-RTT(k|k-1)
(6)
(7)根据当前时刻误差估计协方差P(k|k-1) 和卡尔曼增益Kk更新误差估计协方差P(k|k), 如式(7)所示
P(k|k)=(1-Kk)P(k|k-1)
(7)
(8)最终输出经卡尔曼滤波处理后的RTT(k|k), 即为子流j当前时刻的最优RTT估计值,将其作为端到端时延预测BP神经网络的输入之一。
2.2 基于BP神经网络的端到端时延预测
端到端时延预测的准确性对减少数据包乱序发生具有重要的指导意义。影响链路端到端时延的主要因素包括链路丢包率、吞吐量、RTT等,为实现端到端时延的更准确预测,本文提出构建服务于端到端时延预测的BP神经网络模型,以RTT、丢包率、吞吐量等端到端时延特征参数为输入,端到端时延为期望输出,对设计的多层BP神经网络实施训练,使其通过训练和学习,提高端到端时延预测的准确性。
基于BP神经网络的端到端时延预测主要分为BP神经网络端到端时延预测模型构建和端到端时延预测两部分。其中模型构建部分主要负责构建基于BP神经网络的端到端时延预测模型,通过实验收集的数据样本集对设计的多层BP神经网络模型进行训练,并实施优化,提高端到端时延预测的准确性。
模型构建部分主要由样本数据获取、BP神经网络构建与训练和训练优化3个部分组成。图2给出了这3个部分的组成示意。当应用层有数据传输需求时,端到端时延预测部分将在BP神经网络端到端时延预测模型的基础上,以链路丢包率、吞吐量、RTT等参数为输入,获得链路端到端时延的预测输出。

图2 基于BP神经网络的端到端时延预测模型
2.2.1 样本数据获取
(1)计算、获取丢包率Loss、 吞吐量Th及RTT。 其中RTT由RTT预测部分获取,丢包率Loss、 吞吐量Th的计算方法如式(8)和式(9)所示
(8)
(9)
其中,Cwndpre表示拥塞窗口收缩之前的值,Cwnd表示当前时刻的拥塞窗口值。
(2)计算端到端传输时延EET, 计算方法如式(10)所示[12]
EET=Tr-Ts-Te
(10)
在式(10)中,Tr表示接收端发送SACK的时间;Ts表示发送端发送数据包的时间;Te表示接收端从接收到数据包到发送SACK的间隔时间。
(3)对训练数据和测试数据进行划分。为避免过拟合问题,将经由(1)获取到的样本集划分为训练集和测试集,并设置训练集占比85%,验证集占比15%。考虑到不同维度间的样本数据差距及同维度样本数据间的相差范围,在训练前采用Min-max方法[13]对数据进行归一化处理,将数据映射至区间[-1,1],以减少数据波动对神经网络训练时间及收敛效果的影响。
2.2.2 BP神经网络构建与训练
(1)设置权重、阈值、学习速率、训练最大迭次数等相关参数。初始化权重和阈值在[-1,1]之间。对于学习速率,从较大学习速率开始训练,然后逐渐减小速率,直至损失值不再发散。训练最大迭代次数设置为50 000。在多次试算的基础上,兼顾网络稳定性及训练时长考虑,具体参数设置见表1。
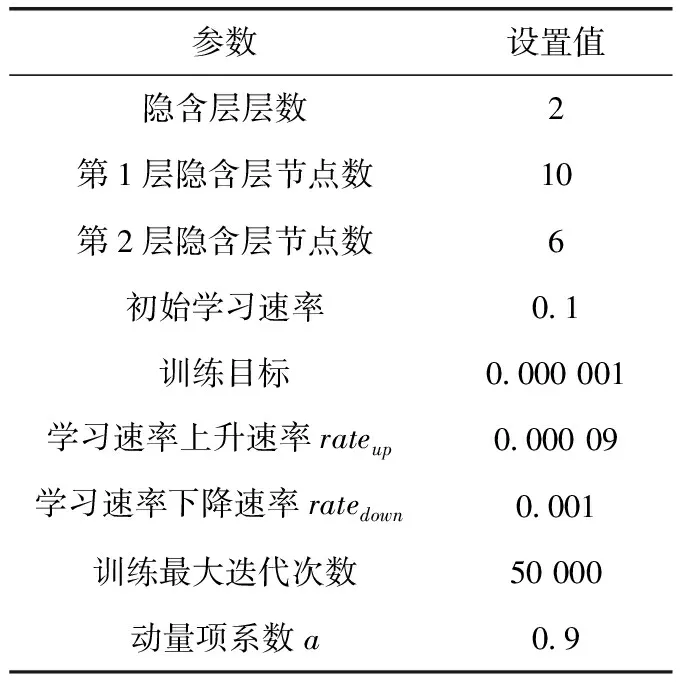
表1 参数设置
(2)输入、输出层神经元个数选择。输入层神经元分别为Th、RTT、Loss,输出层神经元为EET。相应地,输入层神经元个数I设为3,输出层神经元个数J设为1。
(3)隐含层层数和节点数设置。通过获取的样本集,对设置不同隐含层数和节点数的BP神经网络进行训练测试,根据不同神经元个数训练的均方误差来确定隐含层层数和节点数。隐含层节点个数K参考式(11)及测试结果综合选定
(11)
在式(11)中,J为输出层节点个数,I为输入层节点个数,a为1~10间的常数。
(4)随机选取第m个输入样本及其对应的期望输出,将输入样本作为正向传播输入,其中第m个输入样本如式(12)所示,其对应的期望输出如式(13)所示
xi(m)=(Th(m),Loss(m),RTT(m))
(12)
H(m)=EET(m)
(13)
(5)判断训练样本是否用尽,若否,转步骤(6)~步骤(7);否则转步骤(8)。
(6)前向计算各p隐含层及输出层神经元的输入和输出。
1)输入层神经元Th、RTT、Loss计算隐含层输出值Dk(m), 计算方法如式(14)~式(16)所示,其中k表示隐含层节点;i表示输入层节点;I为输入层节点数;xi(m) 表示输入层输入;oi(m) 表示输入层输出;wik表示输入层到隐含层的神经元权值;dk(m) 表示隐含层输入;Bk表示输入层到隐含层的阈值;f为输入层和隐含层激活函数,为正切S形函数(tansig)
oi(m)=f(xi(m))
(14)
(15)
Dk(m)=f(dk(m))
(16)
2)将隐含层神经元的输出值传递给输出层
(17)
Y(m)=g(y(m))
(18)
在式(17)和式(18)中,k表示隐含层节点;K为隐含层节点数;wk表示隐含层到输出层的神经元权值;B表示隐含层到输出层的阈值;y(m) 为输出层输入;Y(m) 为输出层输出。g为输出层激活函数,为线性函数。
(7)误差反向传播,调整连接权值和阈值。计算神经网络输出Y(m) 与期望值H(m) 之间的误差,如式(19)所示
(19)
之后运用梯度下降法,通过反向传播不断调整各层神经元的权值和阈值,使误差函数沿着负梯度方向下降,输出值不断接近实际值。
(8)计算网络全局误差,如式(20)所示
(20)
其中,M代表样本数,H(m),Y(m) 分别代表第m个样本的神经网络输出与期望值。
(9)判断网络全局误差是否满足要求,若满足,预测过程结束;否则查看是否达到设定的迭代次数上限,若已达到,预测过程结束,否则转步骤(4)~步骤(7)。
2.2.3 训练优化
针对权值在学习过程中发生震荡、收敛速度慢等问题,使用动量BP和学习速率可变的BP方法,不断调整各层神经元的权值和阈值,以减小误差,提高BP神经网络的收敛速度。
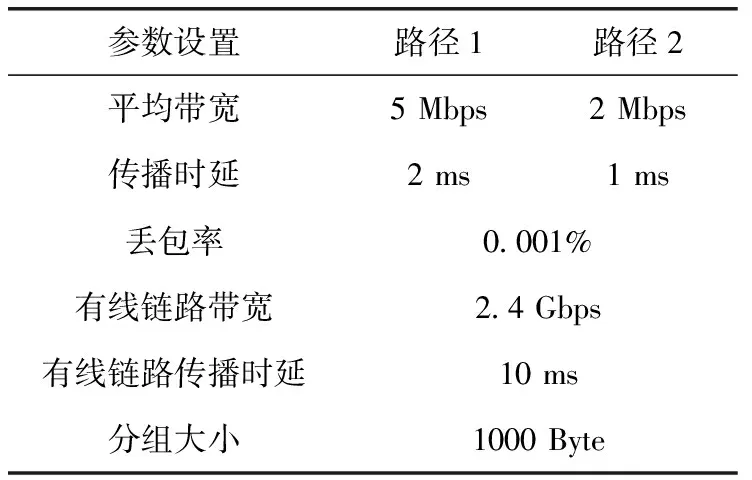
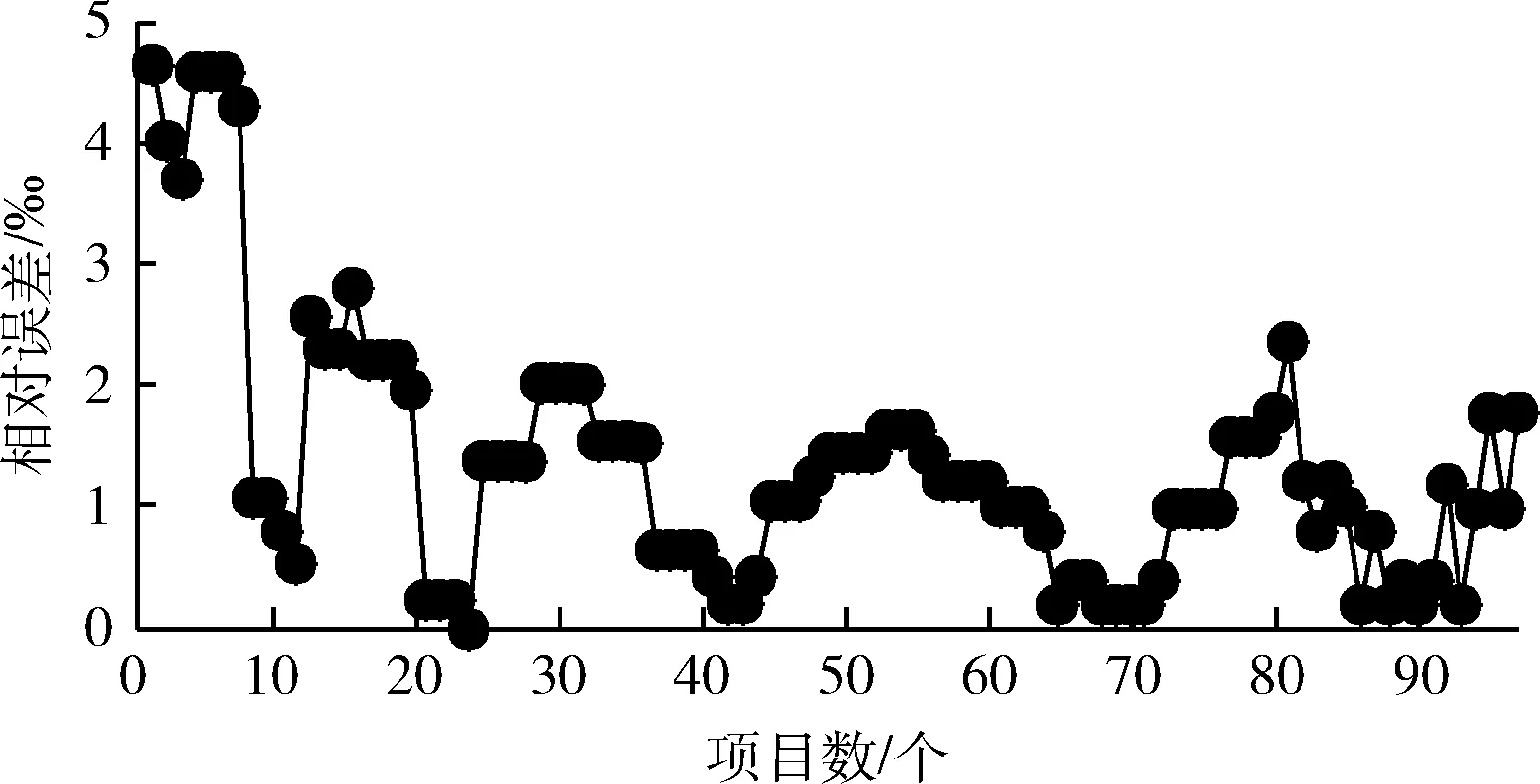
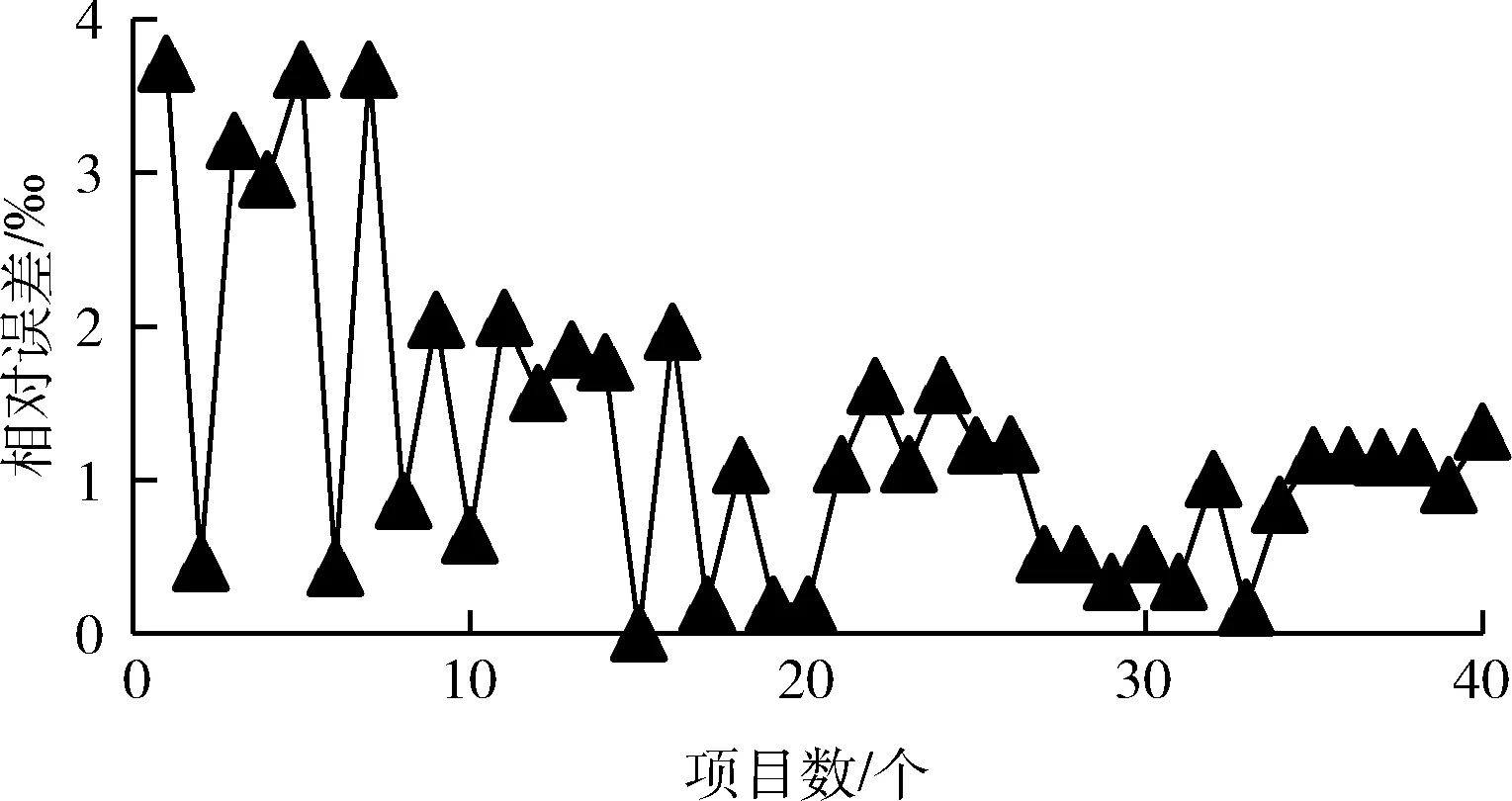
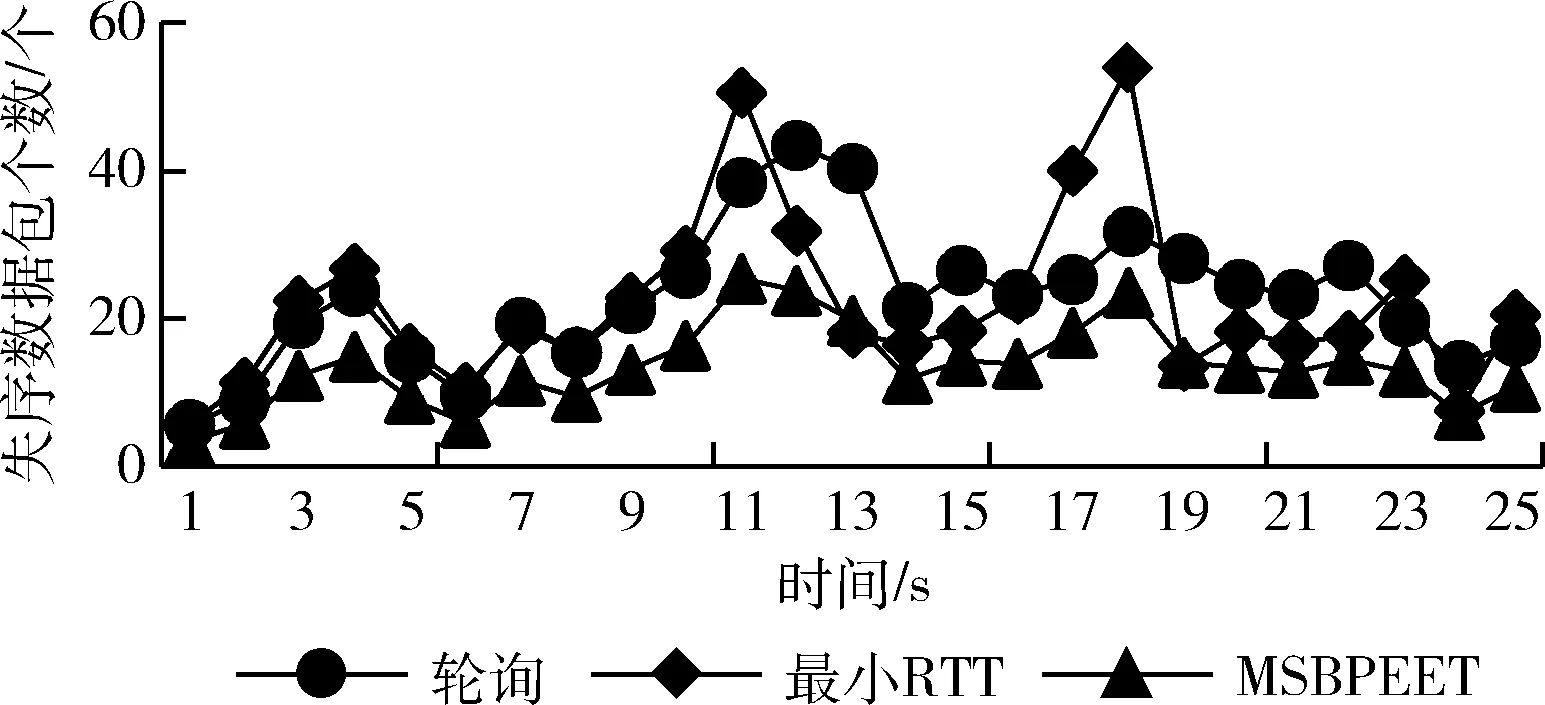
(1)在权值更新时,引入动量因子a(0 w(t)=w(t-1)+Δw(t)+a[w(t-1)-w(t-2)] (21) 在式(21)中,w(t) 代表当前时刻t的权值;w(t-1) 代表上一时刻权值; Δw(t) 代表t时刻权值更新量;w(t-1)-w(t-2) 为上一时刻权值更新量。 (2)根据误差的增减情况对学习速率进行调整:当误差减小时,增加学习速率;当误差增大时,减小学习速率,并撤销上一步修正过程,调整方法如式(22)所示 (22) 其中,η(t) 表示当前时刻t的学习速率;η(t-1) 表示上一时刻的学习速率;e(t) 为当前时刻误差;e(t-1) 为上一时刻误差;rateup和ratedown分别代表学习上升速率和下降速率。 2.2.4 端到端时延预测 利用已训练好的BP神经网络对端到端时延进行离线预测。当存在数据包发送需求时,输入各链路丢包率、吞吐量、RTT,获取端到端时延预测输出结果。算法1给出了该部分工作的算法描述。 算法1: EET_Prediction 输入: 丢包率Loss、 吞吐量Th、RTT 输出: 各子流归一化后的端到端时延EET′j (1) for 任一连接子流jdo (2) if 子流j收到ACK或发生超时 then (3)EETj←BP_EET_Presult(Lossj,THj,RTTj); (4) end if (5)EETmax←Findmax(); (6)EETmin←Findmin(); (7) end for (8) for 任一连接的子流jdo (9)EET′j←(EETj-EETmin)/(EETmax-EETmin); (10) end for 在算法1中,行(1)~行(4)通过BP神经网络预测各子流的端到端时延,其中BP_EET_PResult用于实现在BP神经网络中对子流j的端到端时延预测,其算法描述如算法2所示;之后将预测结果存入EETj中;行(5)~行(6)分别调用Findmax和Findmin求取各子流端到端时延的最大值和最小值;行(8)~行(10)完成对各子流的端到端时延值归一化。 算法2: BP_EET_Presult 输入: 子流j的丢包率Lossj、 吞吐量Thj、RTTj 输出: 子流j的端到端时延EETj (1) for任一连接子流jdo (2)xi=(Lossj,Thj,RTTj); (4)Dk←f(dk); (6)Y←f(y); (7)EETj←Y; (8) end for 在算法2中,行(2)获取输入数据,即子流j的丢包率Lossj、 吞吐量Thj和RTTj; 行(3)~行(4)完成隐含层输入输出的计算;行(5)~行(6)负责将隐含层神经元的输出值传递给输出层,并计算获得输出层的输出,即子流j的端到端时延EETj。 为更有效避免拥塞,减少乱序的发生,在前述工作的基础上,我们进一步提出对子流拥塞状况进行评估。定义子流路径的拥塞程度评估值δj, 用于刻画第j条子流路径的拥塞情况,其计算方法如式(23)所示 (23) 在式(23)中,Unackj表示第j条子流路径已发送但尚未确认的数据包数量;Cwndj为当前子流路径的拥塞窗口大小。 定义链路j的网络状态评估值σj如式(24)所示 σj=αEET′j+βδ′j (24) 其中,EET′j、δ′j分别表示归一化处理后的端到端时延及子流拥塞程度评估值;α、β为参数权重,其选取和调整视实际网络状态而定,α+β=1。 链路的σj值越小代表网络状态越好。 在实施数据调度时,选择有发送窗口的路径形成有效路径集,P={P1,P2,…Pn}, 计算该路径集中各路径Pj的网络状态评估值,当上层应用有数据发送需求时,选择优先级最高,即网络状态评估值最小的路径进行传输,直至该路径的拥塞窗口被填满。若仍有数据需发送,则重新获取路径参数对有效路径集进行更新后再实施上述过程。 算法3给出了网络状态评估及有效路径集排序的算法描述。在该算法中,行(1)~行(3)中的Path_Collecting负责收集有效路径,形成有效路径集Spath; 行(4)~行(6) 对Spath中的各路径计算网络状态评估值;行(7)通过PathSortingandSelect完成根据所求得的各路径网络状态评估值进行排序后,挑选出优先级最高也即网络状态评估值最小的路径pselect, 并将其用于后续的数据包调度。 算法3: OptimalPath_Select 输入:EET′,δ′,α,β 输出:pselect (1)for 任一子流jdo (2)Path_Collecting(Spath); (3)end for (4)for eachpjinSpathdo (5)σj←αEET′j+βδ′j; (6)end for (7)pselect←PathSortingandSelect(); 实验机器配置为Intel(R) Core(TM) i7-4790 CPU,主频3.6 GHz,内存8 GB,操作系统Ubuntu16.04,实验平台为NS-3。实验网络拓扑如图3所示,使用双接口手机终端,Wi-Fi和LTE双路径并行传输。 图3 实验网络拓扑 具体网络参数设置见表2。 表2 实验参数设置 隐含层神经元个数对BP神经网络的训练误差存在较大影响,增加隐含层神经元个数可有效降低BP神经网络的训练误差,但同时也会增加计算量。在实验过程中,设定的隐含层神经元个数超过16时,训练结果趋于稳定;而当隐含层神经元个数超过18时,训练误差增大。因此,综合考虑训练效果及计算效率,最终隐含层神经元个数设置为16。 该部分实验所使用的样本数据来自仿真模拟器,样本数据中的85%用作训练集实施BP神经网络训练,其余部分用作测试集完成对神经网络的测试。 (1)训练误差数据 图4给出了训练阶段的输出误差情况,总体而言训练集样本的相对误差绝对值小于等于5‰,仅有6个样本的相对误差绝对值在4‰~5‰,一个样本在3‰~4‰之间,其余样本均在3‰以下。这表明神经网络的预测输出值与实际值较为接近,所构建的BP神经网络具有较好的端到端时延预测学习能力。 图4 训练相对误差 图5 测试相对误差 (2)测试误差数据 测试集样本经由神经网络学习的相对误差数据如图5所示。所有测试集样本的相对误差绝对值不超过4‰,该相对误差绝对值相较训练相对误差绝对值更低,其中4个样本的相对误差绝对值在3‰~4‰之间,3个样本在2‰~3‰之间,剩余样本都在2‰以下。表明该神经网络可有效完成端到端时延预测的相关学习。 本文以轮询调度和最小RTT调度为比较对象,进行多路传输调度性能分析与比较。 (1)吞吐量 图6给出了轮询调度、最小RTT调度及本文MSBPEET方法的吞吐量数据。其中,MSBPEET在整个传输期间都表现出了相较于另两种调度方法更高的吞吐量,这主要是因为MSBPEET对路径的端到端时延和拥塞状况进行了综合考虑,在调度决策时可更准确地选择合适路径完成数据包发送,使数据包能尽可能按序到达接收端,减少了接收端重排序时间,提升了吞吐量。表3进一步给出了MSBPEET相较于另两种调度方法的吞吐量提升比数据。其中,MSBPEET相比轮询调度吞吐量提升16%,相比最小RTT调度提升了10%。 图6 吞吐量 (2)失序数据包数量 图7给出了轮询调度、最小RTT及MSBPEET这3种方法失序包数随时间变化的数据。在仿真时间段内,轮询调 表3 吞吐量提升比 图7 失序包数 度接收端的失序包数量最多,最小RTT调度次之,这主要是因为轮询调度将所有可用路径同等对待,轮流在各路径上发送数据,从而导致序列号靠前的数据包在路径质量较差的路径上发送而引发失序。而最小RTT调度总是选择RTT最小的子流路径进行数据传输,这样极易出现数据集中涌向低时延路径而导致网络拥塞现象加剧,进而引发丢包和数据包乱序等问题。本文MSBPEET方法,由于实施了更准确的端到端时延预测和路径质量的综合评估,极大地减少了数据包失序的发生。 本文针对移动异构网络环境网络高度动态变化、链路属性差异较大,多路传输极易发生数据包乱序等问题,提出一种基于BP神经网络端到端时延预测的多路传输调度方法,通过构建和训练BP神经网络,对端到端传输时延实施更准确预测,然后优先选择拥塞程度评估值低、优先级高的子流路径进行数据传输,令数据包极可能按序到达接收端,减少数据包乱序发生的可能,在有效避免下一时刻拥塞的同时提高吞吐量。
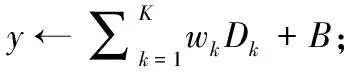
2.3 子流拥塞状况评估
2.4 网络状态综合评估及有效路径集排序调度
3 实验结果与分析
3.1 仿真环境及参数设定

3.2 BP神经网络训练与学习情况
3.3 多路传输调度性能


4 结束语

