基于工况识别的乙烯裂解炉烧焦过程COT随机分布系统建模

陈德坤 万 鑫 赵 众

（北京化工大学信息科学与技术学院）

乙烯裂解炉是生产乙烯的重要设备［1］，在乙烯裂解阶段，由于存在结焦，焦炭层逐渐沉积在裂解炉炉管的内壁上， 这会影响随后的生产过程。 焦炭逐渐积累会增加炉管的热阻、降低其传热效率［2］，并直接导致乙烯装置产量减少、能耗增加，因此当裂解炉炉管内壁上的焦炭积累到一定厚度时必须停止生产，进行烧焦处理［3］。针对裂解炉烧焦过程，智茂轩对乙烯装置裂解炉的实际烧焦参数，结合有限元求解，进行了流程模拟［4］；朱磊和赵众提出基于工况识别的乙烯裂解炉烧焦控制方法，对烧焦控制参数进行调整。 但是国内尚未有针对乙烯裂解炉烧焦过程中炉管出口温度（Coil Outlet Temperature，COT）进行随机分布系统建模的报道［5］。

输出随机分布控制于20世纪90年代末被提出，是随机系统控制的一种新方法。 随机控制和随机估计是控制理论和应用数学领域最重要的研究方向之一［6］，目前已经取得了许多理论和实践成果，如自调整控制最小方差控制、随机线性二次控制等［7］。 随机分布控制直接以系统输出的概率密度函数 （Probability Densinity Function，PDF）或分布函数为控制对象［8］。 在实际工程中，系统中存在大量非高斯随机变量［9］，而且干扰通常是随机的非高斯变量（而不是高斯变量）［10］。 系统实时输出的概率密度函数通常是不对称且多峰的［11］。 期望和方差不能准确反映输出的概率特征［12～14］。对于这些控制对象，常规控制算法通常难以满足要求， 因此需要新的控制算法来实现。Wang H针对具有造纸机背景的非高斯系统概率密度函数控制问题，提出了输出概率密度函数的B样条神经网络模型逼近及梯度优化方法［7］。Guo L和Wang H把系统建模稳定性分析鲁棒控制和状态估计的研究方法与非高斯概率密度函数控制有机结合起来［15］。

烧焦是一个非平稳过程，在烧焦过程中有数十个步骤，依据不同步骤通入空气量和蒸汽量的不同，烧焦过程分为不同阶段，只用随机分布建模方法很难保证建模的准确性。 而且乙烯裂解炉的烧焦过程是个复杂的非稳态操作， 工业过程中，系统操作是默认为稳态的，而实际情况是系统会受到各种扰动和物料波动的影响，工业过程的输入变量会随时间持续改变，所谓的稳态是相对的，而非稳态是绝对的。 对其建模时，有必要先进行工况识别，分工况建模。 为了使建模更加准确，笔者以某乙烯裂解炉的60根炉管出口温度控制为背景，提出基于工况识别的裂解炉烧焦过程炉管出口温度建模方法， 以60根炉管COT的输出概率密度函数通过工况识别进行数据分类，即采用支持向量机（SVM）对数据进行识别进而判定当前工况状态，对数据进行分类后再建模，并使用线性B样条模型进行随机分布建模， 采用递推最小二乘算法求解模型。

1 乙烯裂解炉出口温度控制现状

某乙烯裂解炉烧焦过程选择蒸汽-空气烧焦工艺，向裂解炉逐步通入高温蒸汽，乙烯裂解炉的COT逐步上升。乙烯裂解炉有60根炉管，绕裂解炉一圈，DCS对60根炉管温度求平均值， 得到总COT平均值，再由一个目标值对平均值进行控制。有时候COT的分布较为分散， 当炉管最高温度和最低温度相差过大时，部分炉管升温过快，容易降低管壁的使用寿命，甚至有烧穿的可能［3］，此时必须暂停烧焦，调整COT温度后再继续烧焦，但是会增加烧焦时间，延误生产。

仅针对60个温度的平均值控制， 很难保证COT的分布集中，有必要对COT的输出概率密度函数进行建模， 通过控制输出概率密度函数， 使得COT的分布更为集中，保证烧焦过程顺利进行。

2 工况识别数据分析

裂解炉烧焦过程中有数十个步骤，依据不同步骤通入的空气量和蒸汽量将烧焦过程分为不同阶段 （图1），COT的升温速率在不同阶段也不同， 而烧焦尾气中CO2的含量直接关系到烧焦反应释放的热量，因此可以通过离线测试烧焦尾气中CO2的含量判定当前烧焦过程所处的状态。 根据工业测试结果， 规定当烧焦尾气中CO2含量在2.0%～5.5%时为升温较慢阶段，CO2含量大于5.5%时为升温较快阶段。

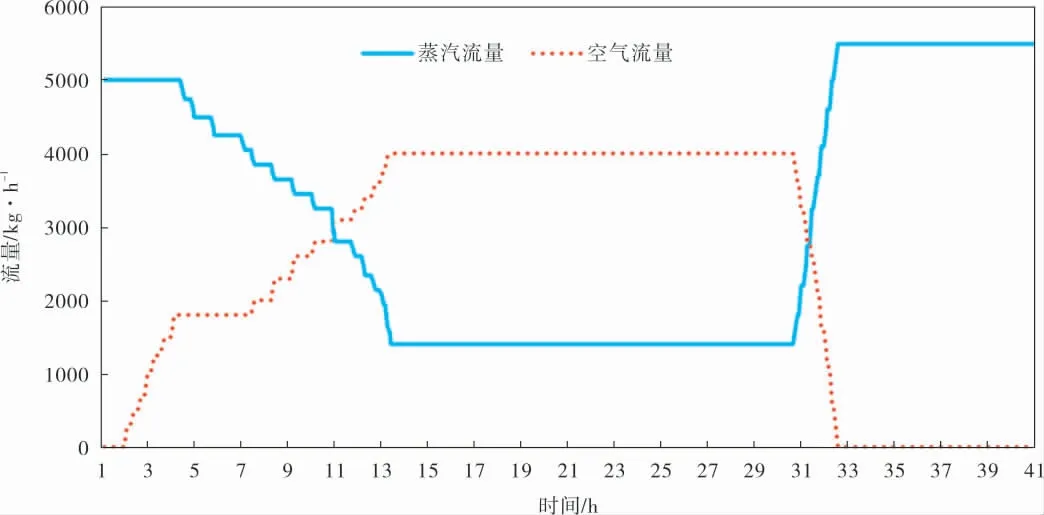
图1 烧焦不同阶段

将离线测试烧焦尾气中的CO2含量作为工况特征， 将离线测试中的60根炉管的COT升温速率分为3类进行样本学习（其中工况0表示当前烧焦过程处于升温速率较快状态， 工况1表示当前烧焦过程处于升温速率较慢状态， 工况2表示当前烧焦过程处于温度较为稳定状态）， 再用于烧焦过程的工况识别， 根据烧焦过程COT的升温速率进行分类。

支持向量机是统计学习理论中常用的方法，在处理小样本、非线性和高维分类问题时有着很多优势［16］。 SVM的主要目的是找到一个超平面来划分要分类的样本， 最大化两种样本之间的间隔，最后将其转化为凸二次规划问题予以解决［17］。 SVM创新地引入了内核函数的概念，为线性可分离问题提供了更好的解决方案。 SVM最优分界面如图2所示， 其中a′=1和a′=-1是待分类的两类样本， 在这两类样本中间存在一条分隔线L将a′=1和a′=-1分为两类。 L1和L2是平行于分隔线L， 并且经过a′=1和a′=-1两类样本中离分隔线最近的两条直线。L1和L2之间为分类间隔，使得两类样本完全分开，分类间隔最大的分隔线即为最优分类线［17～19］。从二维空间扩展到三维空间后，最优分类线转换为最优分类面。 SVM的核心思想就是求出使得分类间隔2/‖w‖最大化的分类超平面H［20］。

图2 SVM最优分界面示意图

以CO2浓度确定训练样本后， 再以温度和温升速率为指标训练SVM分类器，最后对实际工业数据进行分类。

3 对随机分布系统建模

系统的概率密度函数受控制作用的动态影响，乙烯裂解炉的数学模型通常是一个非线性函数，很难得到准确的函数表达式［6］。 因此，笔者对分布样本通过B样条神经网络建模， 得到近似模型。

系统的输入为温度的目标值u（t）；输出为温度的概率密度函数γ（y，u（t）），其形状由系统输入变量u（t）决定。

笔者以COT的输出概率密度函数作为研究和控制对象，分别对3种工况的60个COT的输出概率密度函数通过B样条神经网络建模。 令建模数据样本中温度最大值为Tmax，最小值为Tmin，N为样本总数。 ∀y∈［Tmin，Tmax］，在［Tmin，Tmax］存在N（y）个温度值小于y，近似得到温度y的概率密度函数：

再利用B样条函数建立概率密度函数与权系数之间的关系［12］：

其中，gi为控制输入u（t）的相关权值；Bi（y）是预先选定的基函数；e0是逼近误差，n为B样条密度函数个数；u（t）离散化为uk。 对乙烯裂解炉的出口温度实际输出的概率密度函数用B样条模型来进行逼近，由式（2）得到权值。

对于连续线性B样条模型，其离散系统为：

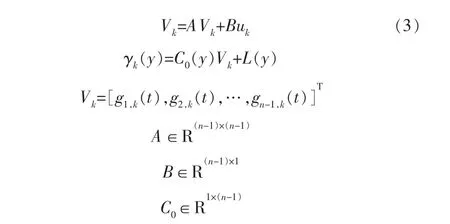
其中，L（y）为插值；Vk、A、B为常数矩阵；C0（y）为常函数矩阵。

令：

令z-1表示单位延迟算子（即z-1uk=uk-1），并记fk（y）=γk，系统状态空间的形式就可以表示成如下的输入输出形式：

其中，系数ai和向量Dj可以通过下式获得：

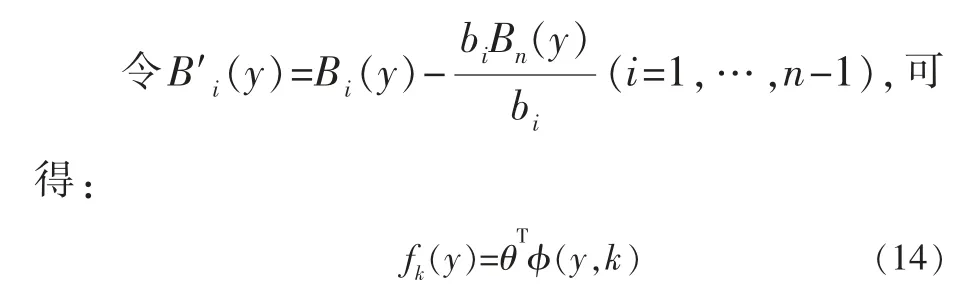
此方程对于∀y∈［Tmin，Tmax］均成立，故任意选择一个序列Y={yi∈［Tmin，Tmax］}（i=1，…，M），可得：

采用递推最小二乘法来估计相应的参数：

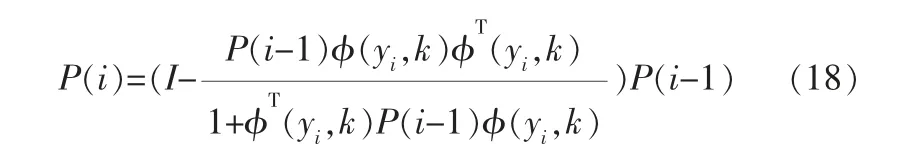
θ（M）为θ在k时刻的估计值。 令初始条件θ（0）=θ0，P（0）=104ln（1+n）。 由估计的参数，得出相应的矩阵A、B［6，21］。

针对不同的工况i=0，1，2， 建立的离散系统为：

4 工业应用实例

将烧焦过程中采集的数据样本随机分为训练集和测试集，样本信息详见表1。

表1 样本信息

烧焦过程工况2较好分类， 所以用SVM对工况0和工况1进行分类。

以CO2浓度确定训练样本后训练SVM分类器，对测试集进行分类。 训练集和测试集样本的分类结果如图3、4所示。

图3 SVM训练集数据分类

分类结果准确率为正确分类样本数与测试集样本总数的商的百分数。 该分类器分类准确率为88%， 说明它可以将较快升温段与较慢升温段较为准确地分开。

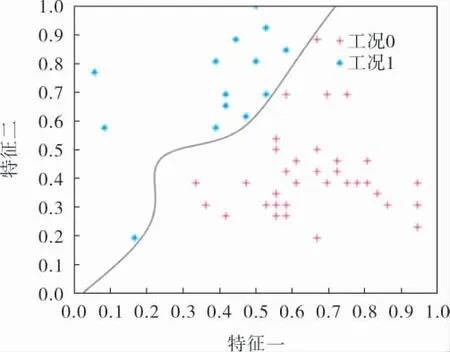
图4 SVM测试集数据分类

通过工况识别对数据进行分类后得到烧焦过程中的3组COT数据， 把每组数据分成两部分：一部分为训练数据，用于计算出模型；另一部分为测试数据，用于对模型进行测试。 每部分选取5 min内60根COT值，每5 s取1个，共3 600个值，用笔者方法得到概率密度函数， 将定义区间分为8个子区间， 以6个三阶B样条函数为基函数构建B样条神经网络， 分别对3个温升速率不同段进行建模，并验证其结果。

较快升温段建模结果如图5所示， 升温速率大，裂解炉炉内反应剧烈，应设法降低升温速率。从测试结果来看， 较快升温段升温速率较为分散，且整体偏高。

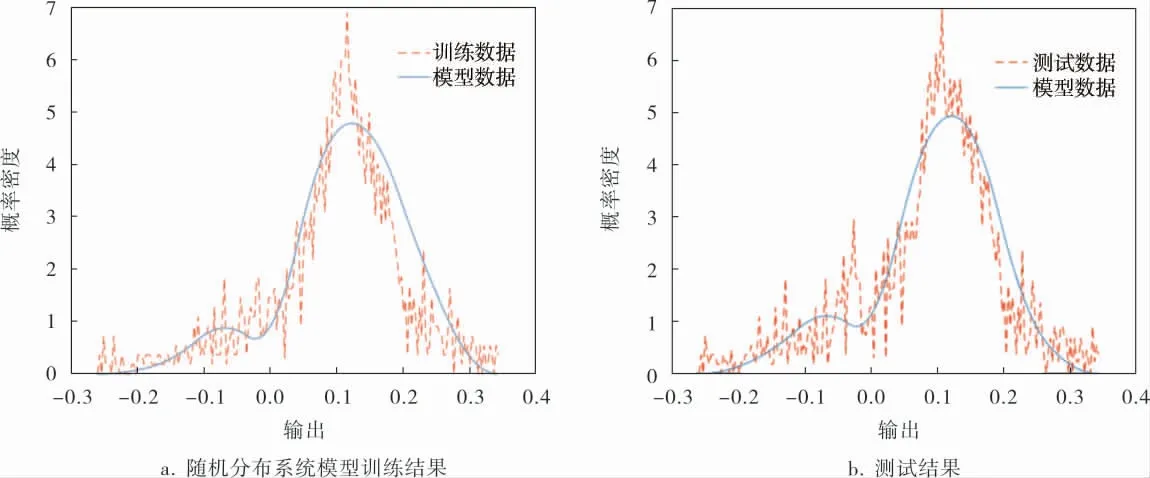
图5 较快升温段建模

计算结果：

升温较慢段建模结果如图6所示， 升温速率较小，裂解炉内反应不剧烈，但相对于温度平稳段整体温度分布较为分散，此时烧焦刚开始或者即将平稳。

图6 较慢升温段建模

计算结果：

温度平稳段建模结果如图7所示， 温度平稳段建模结果可视作升温速率为零，此时温度分布较为集中，烧焦整体处于平稳阶段。

图7 温度平稳段建模

计算结果：

3个阶段的测试结果表明， 模型趋势与实际数据相当，且与实际工况相符，可以代表当前阶段裂解炉炉温分布情况。

误差率为样本概率密度函数与建模概率密度函数之差绝对值的百分数，本方法建模误差的计算结果见表2。

表2 建模误差%

将实际工业数据与模型数据对比后可以看出， 模型预测值与实际工业值大致趋势相同，误差在可接受范围。

5 结束语

提出基于工况识别的随机分布建模方法，针对乙烯裂解炉烧焦的非平稳过程， 以COT温升速率为指标进行工况识别，对烧焦过程中乙烯裂解炉COT的概率密度函数建立概率密度函数模型，工业数据验证了所建模型的可行性，为实现乙烯裂解炉的烧焦过程进行随机分布先进控制奠定了基础。