基于相对增益矩阵的多FACTS交流输电系统交互影响研究

徐玉林 张寿明

（昆明理工大学信息工程与自动化学院）

随着智能电网的发展与革新， 电网结构变得越发复杂，电网的运行变得非常沉重。 柔性交流输电（FACTS）技术的出现正好解决了上述问题，因此得到快速发展。 FACTS技术使得电网运行更加安全、稳定和可靠，而且经济性也得到提高，它使得多种性能的FACTS装置被发明。例如，静止无功发生器（SVG） 为电网提供连续变化的无功功率，补偿电网无功功率使其保持平衡；静止无功补偿器（SVC）的作用是吸收或者提供电网的无功功率，使电网的无功功率趋于平衡；统一潮流控制器（UPFC）可以通过电压注入，控制线路的阻抗、电压和功率，使得线路不管是电压还是功率等都趋于平衡；静止同步补偿器（STATCOM）可以控制输出点的电流，以此控制节点处的电压幅值或者功率大小。 学者们在电力系统的建模和对FACTS交互影响方面做了很多的研究［1～5］，并且发现FACTS技术在使用中有许多优点，市场应用广泛。 许多学者研究发现，在电力系统使用FACTS装置时，使用单一的FACTS装置是可以改善系统性能的，但是接入多台同种FACTS装置或者不同种FACTS装置后有可能使得电力系统变得不稳定。 多台FACTS装置之间会产生一定的影响，影响严重时，会让电力系统失去稳定性。 文献［6］研究了静止无功补偿器的两个控制性能间的相互影响，结果表明其作用是互相抵触的。 文献［7］的研究表明静止同步补偿器的两个控制性能间也有可能存在相互影响，影响严重的情况下会使得电网运行变得不稳定。文献［8，9］研究了接入FACTS装置的Phillips-Heffron 仿真模型， 运用相对增益矩阵（RGA）分析，表明单机无穷大电力系统中接入不同的FACTS装置之后存在负交互影响， 但是运用Phillips-Heffron模型求解过程非常繁琐，不利于多机多区域电力系统模型的求解。 对于以上问题，笔者运用线性化状态空间法，建立电力系统输配电模型，求解过程简单直观，可以使用在多机多区域电力系统中。 笔者仿真建立的电力系统模型使用的是四机两区域电力系统，在系统中加入静止无功补偿器和静止无功发生器，并且根据此线性化模型求解出电力系统的传递函数， 同时利用RGA和NI指数分析方法， 分析FACTS之间的负交互影响关系，最后根据时域仿真的结果与笔者提出的两种分析方法相互印证结果的可靠性。

1 电力系统模型的建立

仿真使用的电力系统模型为四机两区域模型， 其中同步发电机采用的是三阶实用模型，同步发电机的数学模型如下：

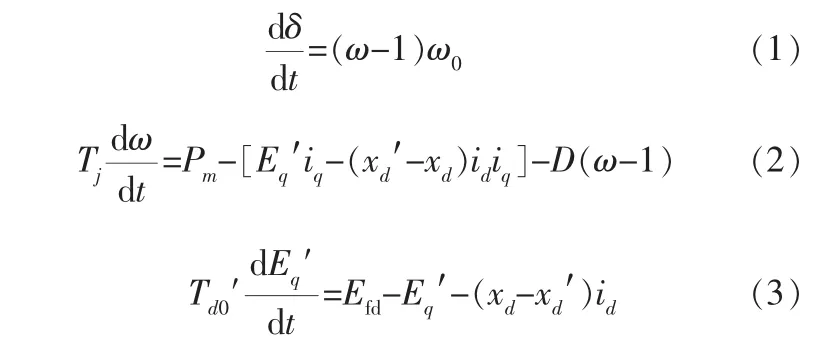
其中，δ为转子摇摆角；ω为转子角速度；ω0为转子额定角速度；Tj为惯性常数；Pm为原动机的输入机械功率；Eq′为暂态电势；xd为直轴同步电抗；xd′为直轴暂态电抗；id、iq分别为直轴和交轴定子电流；D为阻尼转矩系数；Td0′为直轴暂态开路时间常数；Efd为励磁电压。

同步电机的励磁系统模型使用文献 ［10］中的模型，公式如下：

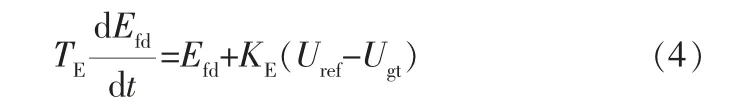
其中，TE、KE分别为励磁时间常数和等值增益；Uref、Ugt分别为端电压的设定值、端电压。

静止无功补偿器使用的数学模型如下：

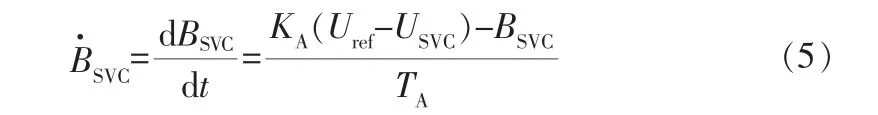
其中，BSVC为静止无功补偿装置的等效输出电纳，KA、TA分别为静止无功补偿装置中的比例增益和时间常数。

静止无功发生器使用的数学模型如下：

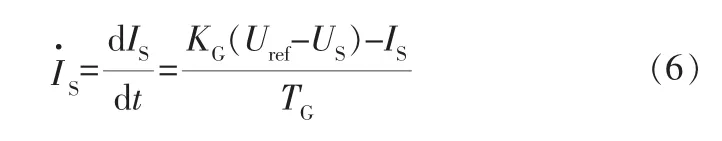
其中，IS为静止无功发生器装置的等效注入电流，KG、TG分别为静止无功发生器装置中的比例增益和时间常数。

在电力系统线性化模型中，由这些电力系统模块组成的电力系统模型的动态过程可以用以下公式表示：

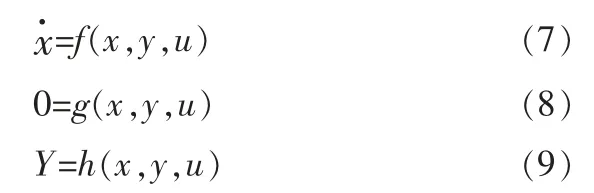
在式（7）～（9）中，选择状态变量为：同步电机的δ、ω、Eq和Efd；选择代数变量为电力系统中各个母线电压。 笔者研究的是静止无功补偿器和静止无功发生器之间的影响关系，所以选择BSVC和IS为控制变量。 由式（7）～（9），对电力系统的状态方程进行线性化处理后，得到电力系统的状态空间表达式为：

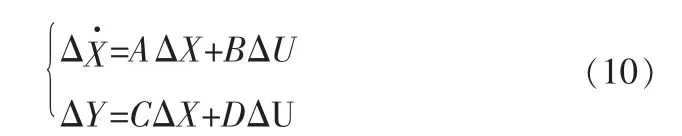
其中，A、B、C、D为系数矩阵。

由上述状态空间表达式可以求出电力系统的传递函数：

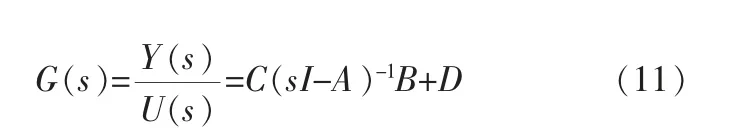
2 相对增益矩阵和NI指数分析方法

2.1 相对增益矩阵

在多变量控制系统中，相对增益矩阵［11］是一个分析交互影响可靠的分析方法。 RGA分析方法描述的是对于一个多变量控制系统，当改变其他的回路参数时，对于没有改变的控制回路的影响大小。 对于一个方阵的控制电力系统，可以由下面的公式求出RGA矩阵的每一个元素的数值：

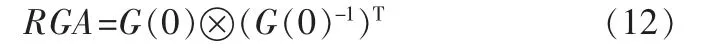
其中，符号⊗表示RGA矩阵在稳态值下的矩阵对应元素的乘积， 也就是常说的Hadamard乘积；G（0）是电力系统传递函数G（s）的稳态值。 笔者采用的是简单的双输入双输出系统，其中接入静止无功补偿器和静止无功发生器装置，其控制系统如图1所示。 运用RGA分析，笔者不考虑电力系统的动态过程， 把BSVC和IS作为电力系统的输入， 把接入FACTS装置的母线电压作为电力系统的输出。

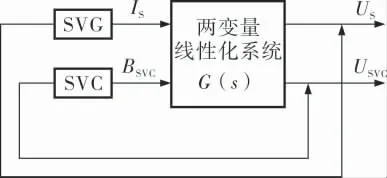
图1 两变量闭环控制系统

电力系统的二阶相对增益矩阵有如下的特点：

a. 每行每列元素之和等于1。

b. 若对角元素为负数，则由于控制变量的影响，控制系统变得不稳定。

c. 若元素为1， 则控制变量之间不存在交互影响；元素值越接近1，则控制变量间的交互影响越小；若元素值大于1，则说明两个控制变量间存在负交互影响，此时两个控制效果互相抵触。

2.2 NI指数

在分散控制系统中，NI指数也是一种常用在控制系统中的变量配对方法［12］，NI指数还可以判定整个控制系统的稳定性［13］，其计算公式如下：

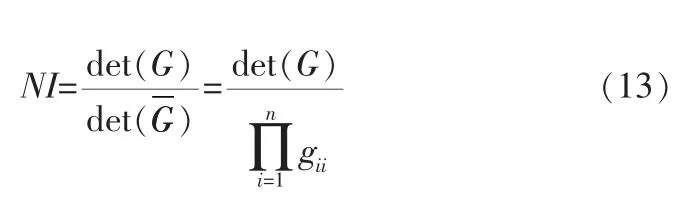
其中，G为稳态相对增益矩阵，det（G）为相对增益矩阵的行列式，det（G）为相对增益矩阵各对角线元素的乘积［14］。

NI指数分析方法有如下结论：NI指数小于零，则控制系统一定不稳定；NI指数大于零，则控制系统稳定与不稳定都有可能，但是一般情况下是稳定的。 对于一个双输入双输出的系统，NI指数大于零一定是稳定的，而且NI指数越接近1，交互影响越小。

由上述可得RGA+NI的分析方法， 该方法判断交互影响的标准为： 首先计算出控制系统的RGA矩阵，根据RGA矩阵元素来判断两个控制变量间交互影响的大小；然后计算出NI指数，并判断NI指数的正负，从而确定系统是否稳定，并根据NI指数接近1的情况来判断系统整体交互影响的大小。

3 算例分析

本研究的仿真系统采用四机两区域电力系统［15］，如图2所示。 该系统在母线7和母线9处装设有静止无功补偿器和静止无功发生器，系统的线路参数见表1。

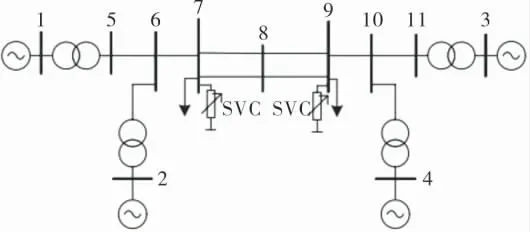
图2 安装两台SVC的四机两区域电力系统模型

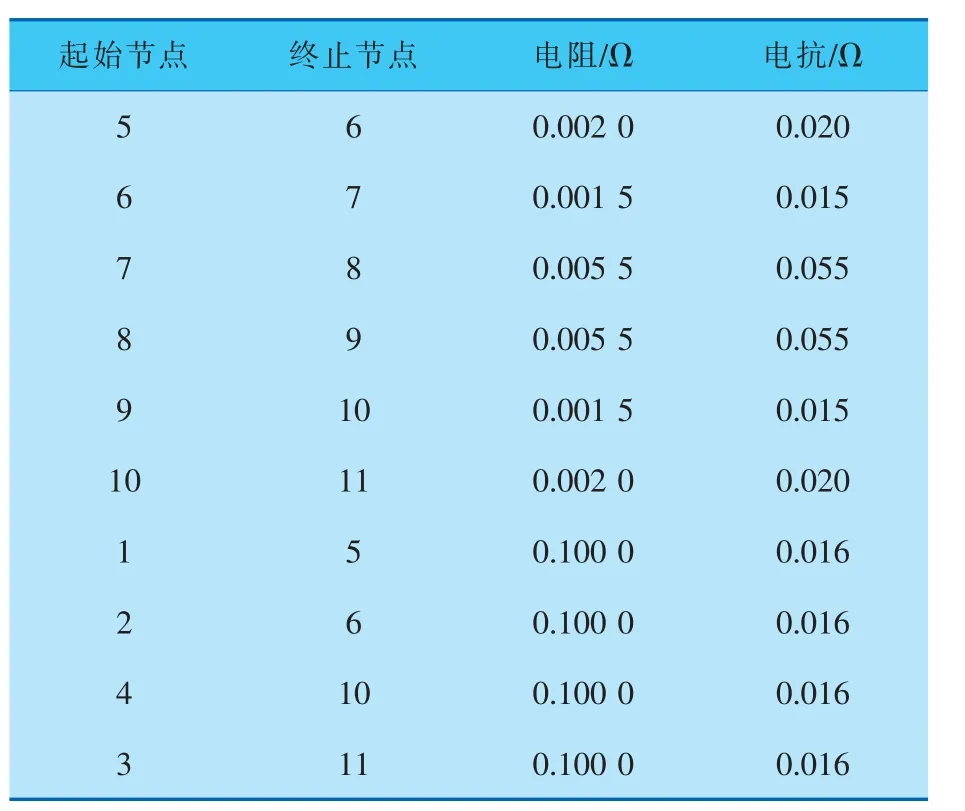
表1 系统线路参数

3.1 两台SVC间的交互影响分析

在四机两区域电力系统中， 两台SVC分别接入母线7和9， 安装SVC在电力系统中可以吸收或者提供电网的无功功率，从而保持电压恒定并且维持电网无功功率平衡。 在系统中取SVC装置的比例增益KA为200、时间常数TA为0.05。

在此电力系统中，改变电气距离也可以定义为改变母线7和9之间的阻抗。 把母线7到9的原始阻抗定义为弱耦合线路；把母线7到9之间的阻抗减少一半定义为中耦合线路；把母线7到9之间的阻抗减少至四分之一定义为强耦合线路，具体阻抗为：

弱耦合 0.011+j0.11

中耦合 0.0055+j0.055

强耦合 0.00275+j0.0275

仿真的过程中，在0.4 s时，将其中一台SVC装置的参考电压提高2.4%，另一台保持不变，仿真得出两台装设SVC处节点的实际电压如图3、4所示。

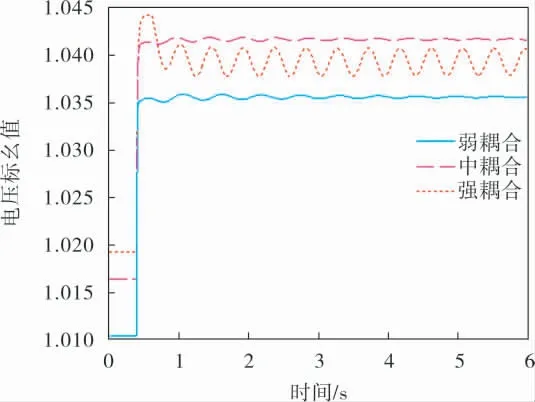
图3 两台SVC联合运行时母线7实际电压曲线

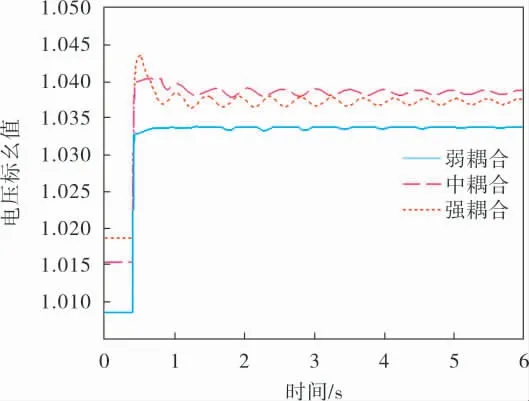
图4 两台SVC联合运行时母线9实际电压曲线

根据线性化模型计算出此系统的RGA矩阵和NI指数，结果见表2。

表2 两台SVC间不同耦合程度时的RGA矩阵和NI指数

3.2 SVC和SVG间的交互影响分析

仿真时保持电力系统模型参数等不变，SVC控制参数也不变，在母线9处换上SVG。 在系统中取SVG装置的比例增益KG为100， 时间常数TG为0.05。

仿真的过程中，在0.4 s时，将SVC的参考电压提高2.4%，另一个装置参数保持不变，仿真得出节点7处的实际电压如图5所示。

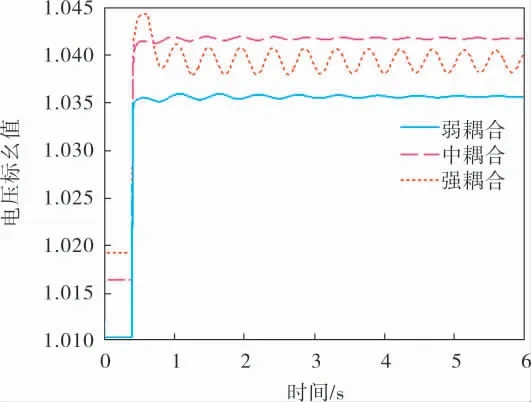
图5 SVC和SVG联合运行时母线7实际电压曲线

仿真的过程中，在0.4 s时，将SVG的参考电压提高1.5%，另一个装置参数保持不变，得出节点9处的实际电压如图6所示。

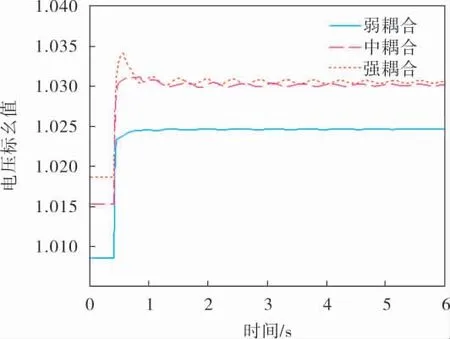
图6 SVC和SVG联合运行时母线9实际电压曲线

根据线性化模型计算出此系统的RGA矩阵和NI指数，结果见表3。

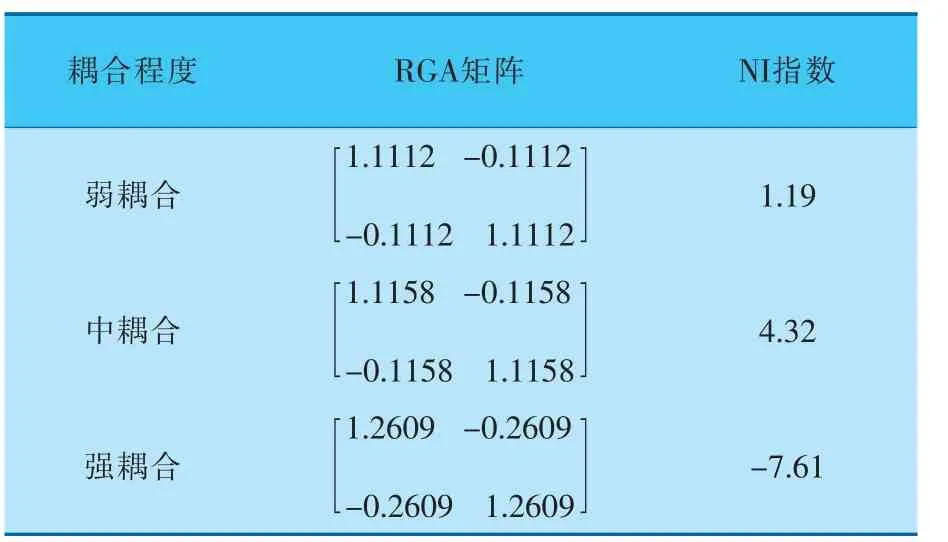
表3 SVC和SVG间不同耦合程度时的RGA矩阵和NI指数

由图3～6可知， 不管FACTS装置是否同种，在装设FACTS装置的两个母线之间电气距离较远（即母线间阻抗较大）时，装设有FACTS装置处的母线电压可跟随参考电压的变化而变化。 但在装设FACTS装置的两个母线之间电气距离较近（即阻抗较小）时，装设有FACTS装置处的母线电压很难跟随参考电压的变化而变化，而且电压相较于电气距离较远时波动较大。由此可以得出，FACTS间的负交互影响随着电气距离的减小而增加，从而影响了SVC和SVG的控制性能。

由表2、3可得，RGA矩阵的对角元素都大于1，可见，不管是否同种FACTS装置，它们之间一定存在交互影响， 而且电力系统中加入多台FACTS装置必然会使两个FACTS装置间相互干扰， 一台FACTS装置的接入必然会降低另外一台FACTS装置的控制效果。 电气距离的增大，也会使RGA矩阵的对角元素越来越偏离1，NI指数也会偏离1，这样就会使负交互影响变得越来越大。 当负交互影响超过一定的程度时， 系统会失去稳定性，这样就与时域仿真的结果相互印证。

4 结束语

采用RGA矩阵和NI指数分析方法，分析了由状态空间建立的四机两区域电力系统模型的交互影响。通过两种方法的分析，得出两种FACTS装置的交互影响大小与电气距离的关系：电气距离越小，负交互影响越大，时域的仿真结果也对此进行了印证。