基于TSNS和KNN规则的复杂多阶段过程故障检测

李 元 耿 焱 冯立伟，b

（沈阳化工大学a.过程故障诊断研究中心；b.理学院）

现代工业生产过程通常具有动态性、非线性及多阶段性等特征。 常见的具有多阶段结构特征的工业过程有半导体蚀刻工艺［1，2］、芯片封装工艺［3］和青霉素发酵过程［4～7］。 为了提高控制系统故障检测的性能，近年来在该研究领域，主元分析（Principal Component Analysis，PCA）［8，9］、 核主元分析 （Kernel Principal Component Analysis，KPCA）［10，11］、偏最小二乘［12］及独立元分析［13］等方法应用广泛。 其中PCA监控策略是一种广泛应用的线性降维方法。 针对工业生产过程中的数据存在非线性的问题，采用了KPCA方法［14，15］，但是该方法未能考虑多阶段性和动态性特征的不利影响。考虑工业过程具有动态性特征，Ku W等提出了DPCA （Dynamic Principal Component Analysis，DPCA）［16］， 该方法能够处理数据的动态信息，剔除数据样本间的相关性。 但是它也要求过程数据满足单一阶段的同一分布的基本假设，在多阶段过程中故障检测率［17］较低，无法实现对多阶段过程的有效监控。

针对具有的多阶段性和非线性特征的工业过程数据的检测问题，国内外众多学者提出一系列有效的方法应用于多阶段工业过程［18～21］。He Q P和Wang J提出以累积近邻距离作为检测指标的K近邻规则（K Nearest Neighbor Rule，KNN）故障检测方法［18］。 针对多阶段过程数据方差差异大的问题，冯立伟等提出特定距离的K近邻方法［19］，然而，当工业过程具有较强的动态性时，检测效果相对较差。 马贺贺等提出局部离群因子（Local Outlier Factor，LOF）［20］，刘帮莉等提出运用局部密度估计方法对多阶段过程实现故障检测［21］，但这两种方法对动态过程的监控效果不佳。 冯立伟等提出基于时空近邻标准化和局部离群因子（Time-Space Nearest Neighborhood Standardization and Local Outlier Factor，TSNS-LOF）的方法［22］，该方法考虑了时间和空间近邻信息，相对于上述多阶段方法，检测效果明显提高。 但是它的每个数据点都要分配依赖邻域密度的离群因子，同时还需求出全体采样点的离群因子，计算所需的时间较长。

综上，为了进一步提高非线性、动态性与多阶段性特征系统的可靠性、稳定性，笔者提出一种基于时空近邻标准化和K近邻规则（Time-Space Nearest Neighborhood Standardization and K Nearest Neighbor Rule，TSNS-KNN） 的故障检测方法，首先在时间维度上搜索到训练样本的近邻样本集，其次在空间维度上寻找上述样本集的近邻样本集，并进行标准化处理，最后利用标准化的训练样本集计算样本的累积近邻距离，将该值作为检测的指标进行在线故障检测。 TSNS-KNN方法与局部离群因子的复杂过程故障检测方法相比适用范围更广且计算时间相对较短。

1 K近邻方法

在训练样本数据集中，首先查找样本xi的前k个近邻样本，并计算xi到前k个近邻样本之间的距离，然后计算前k个距离的平方和，并把它作为统计指标：

K近邻方法分为离线建模和在线检测过程。

离线建模过程如下：

a. 从训练样本集X中查找样本x的前k个近邻样本；

在线检测过程如下：

a. 从训练样本集X中寻找待检测样本xγ的前k个近邻样本；

2 基于时空近邻标准化和K近邻规则的检测方法

2.1 TSNS-KNN模型构建

将样本x标准化可得：

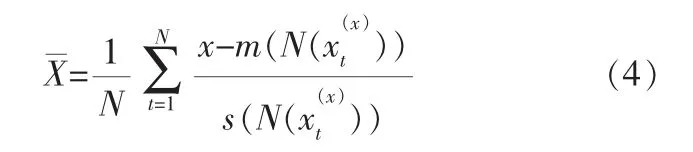
正常样本具有一组相似的时间近邻样本集与空间近邻样本集。 通过TSNS处理后，正常样本会接近坐标原点， 而故障样本会偏离正常样本。TSNS方法能够保留故障样本与正常样本的差异性。 考虑单纯使用空间近邻信息所导致的错误检测，TSNS方法充分考虑时间序列信息的影响，使用来自于相近时刻的样本近邻集，最后对过程使用KNN方法进行检测。

下面利用Lyapunov中心极限定理［24］证明包含动态性和多阶段的数据通过TSNS方法处理后近似服从单一正态分布。

如果存在δ＞0时，Lyapunov条件满足，则（xjμj）/sh的和在h有限时收敛于标准正态随机分布，即：

判断Lyapunov条件成立［25］，一般要求δ=1。 在具有动态性和多阶段性的数据集中， 样本x虽然来自不同的阶段，对于正常样本xi来说，样本xi与其时间和空间层面的近邻组成的序列集合属于同一阶段，其期望值和方差与近邻集均值和近邻集方差相同。 Lyapunov条件有如下形式：

因同一阶段的数据服从高斯分布时， 可满足Lyapunov条件。故根据Lyapunov中心极限定理可得：

尽管在多阶段数据集中，样本来自不同的阶段，但是对每一个样本而言，其Lyapunov条件总是能够得到满足，即经过TSNS处理之后的样本都可以近似服从标准正态分布，此时每个样本之间是独立的，即消除了过程的动态性。

2.2 TSNS-KNN故障检测方法

2.2.1 离线建模

离线建模步骤如下：

2.2.2 在线检测

在线检测步骤如下：

2.3 动态非线性数值实例

使用一个动态非线性的数值仿真实例阐述该方法。该过程有两个输入变量θ和t，两个输出变量x1和x2，模型如下：

其中，θ的取值范围为-2π～2π，t的取值范围为0～4π，e1、e2是随机噪声，a是取值为0.2的过程参数。

首先确保整个过程正常运行并生成500个建模样本。其次保证过程再次正常运行，但从t=2π开始， 在变量x1上加入幅值为-6的阶跃型扰动故障，直到过程结束。 原始数据如图1所示，可以看出有大量故障很接近正常训练样本。 运用TSNS-KNN方法监控整个过程，其中时空近邻标准化后的结果如图2a所示， 从图2a中看出TSNS方法对数值实例实现了故障样本和正常样本的分离，TSNS-KNN方法的检测结果如图2b所示， 由图2b可见对测试数据的故障检测效果较好。

图1 原始数据散点图

图2 TSNS-KNN方法的非线性动态过程检测结果

3 TSNS-KNN方法在青霉素发酵过程的应用

在青霉素发酵过程中，观测变量随着时间的变化而发生改变，且前一时刻的样本会影响后一时刻的样本，因此其具有动态性，过程中的样本间也具有较强的自相关性，同时变量之间也具有非线性。 经过时空近邻标准化处理后（图3），样本的时刻相关性降低，同时消除了过程中的动态性特征。 原始数据的相关性如图4a所示，经过TSNS方法处理后，将具有动态性和多阶段性的原始样本转化为单一阶段样本，如图4b所示，并完成了故障样本和正常样本的分离。 青霉素发酵过程的第1阶段是青霉菌适应生长繁殖阶段，第2阶段青霉素作为二次代谢的产物开始合成，青霉菌开始生产青霉素。 青霉素发酵过程的数值仿真在Pensim平台上［7］，已经有相关研究成果表明该仿真软件具有较高的实用性和有效性［19］。 笔者使用Pensim平台模拟生产数据，总模拟时间设置为400 h，采样间隔为0.5 h。 首先，所有系统采用默认参数来建模，产生一组正常批次数据。 其次，加入阶跃信号和斜坡信号在变量底物流速率上，并设定不同的故障幅度，此故障设有不同的引入时间，其中终止时间均为400 h。 其余参数均采用默认值，生产5个批次故障数据，故障数据的详细描述见表1。

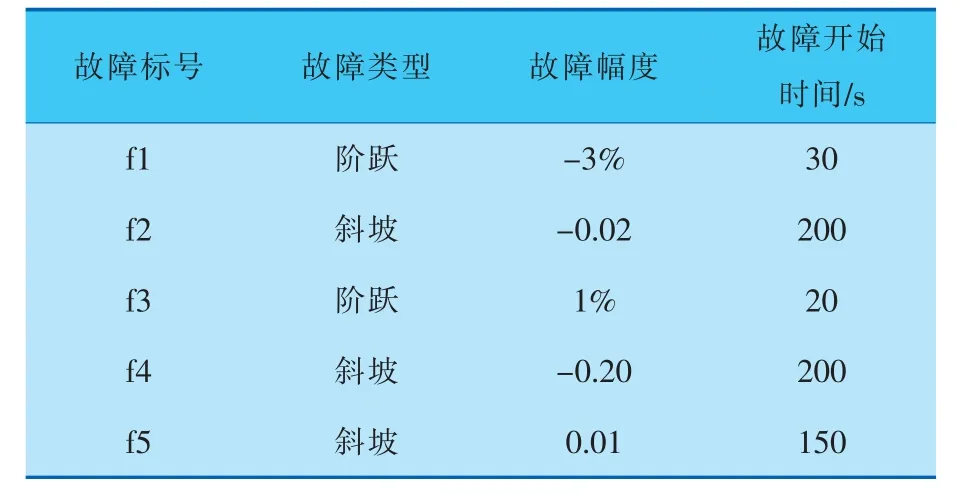
表1 故障样本

图3 样本相关性

图4 青霉素过程数据

运用TSNS-KNN方法， 解决青霉素发酵过程中的动态性、非线性和多阶段性问题，检测结果优于文中其他方法。 运用PCA、KPCA、DPCA、KNN、TSNS-LOF和TSNS-KNN方法进行检测对比。TSNS-KNN方法的置信水平均取95%；PCA、KPCA方法依据85%的累计贡献率［25］选取主元个数；KPCA中的高斯径向核函数中的参数取3 500；DPCA方法的时滞参数［26］取2，主元个数选择为5；KNN的近邻个数选择为5；TSNS-LOF方法与TSNSKNN方法的近邻个数N=5，K=5，k=5。 测试集中故障f5的检测图如图5所示，测试集所用方法的故障检测率列于表2， 由表2可见TSNS-KNN方法检测效果相对较好。

表2 不同方法的故障检测率%

图5 故障f5检测结果

如图5a所示，PCA方法检测上述故障效果相对较差， 因为PCA方法要求数据来自单一阶段的独立正态分布，由图4a可知，该过程是具有非线性和多阶段性特征的过程，因此无法做出准确的检测；如图5b所示，KPCA方法无法捕捉数据的动态性特征，所以检测效果相对低下；如图5c所示，DPCA方法能够提取复杂过程的动态特征， 但是它的统计量需要满足单阶段的多元正态分布的假设， 所以对多阶段过程的故障检测率也比较低； 如图5d所示，KNN方法能够解决非线性和多阶段特征问题， 但是它无法检测过程的动态性，部分故障检测效果不显著； 如图5e所示，TSNSLOF方法在线检测实时性要求较高， 必须求出所有样本采样点的离群因子， 从而计算时间长，检测时间见表3；如图5f所示，TSNS-KNN方法相比其他方法，检测效果相对更优，因为该方法消除了样本之间的动态相关性。

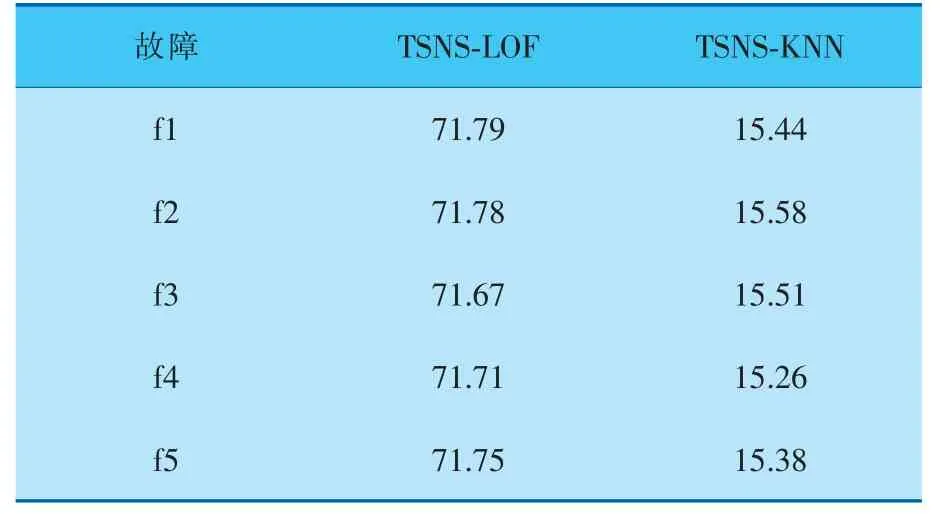
表3 测试集的检测时间s

4 结束语

针对复杂工业过程的动态性、非线性和多阶段性的特点，笔者提出了基于时空近邻标准化和KNN规则的复杂阶段过程故障检测方法。 TSNSKNN方法将时序信息考虑在内， 能够克服非线性、动态性和中心漂移的不利影响。 将TSNS-KNN应用在青霉素发酵过程中，实验结果表明：TSNSKNN方法相对于PCA、KPCA、DPCA、KNN和TSNSLOF方法具有更高的及时性和故障检测率， 针对多阶段过程和动态过程的故障，具有较高的检测能力，笔者所提方法能够更好地保障生产过程的安全和产品高质量的动态性特征。