基于DSP的振动信号自适应采样设计
吴恩奇 汪国阳 杨振国 段汝良
(浙江中控技术股份有限公司)
在工业应用中, 旋转机械设备必不可少,常见的有汽轮机、燃气轮机、轴流式压缩机、风机及泵等。 由于制造与生产条件所限,这些设备在旋转工况下会在各个方向产生位移,一般转轴径向位移(也称其为径向振动)频率较高[1]。 径向振动的频率、幅度等参数可以很好地表征设备的运行状态和“健康”状态,如通过对振动状态的分析,可以提前识别主轴裂纹、转子掉叶等故障,因此在设备监测中起到至关重要的作用[2]。
工业领域的大型旋转机械设备的振动状态主要由透平监测系统(Turbine Supervisory Instrumentation,TSI)进行监测、分析与报警[3]。 TSI系统监测的参数包括振动、位移、转速、键相及温度等,其振动监测功能主要对径向振动波形信号进行时域分析和频域分析[4],其中频域分析需要进行复杂的快速傅里叶变换 (Fast Fourier Transform,FFT),因此对采样点数和采样频率有更严格的要求[5]。 为了满足FFT运算要求,常用的方法是延长采样时间或对采样点进行补零,但这样处理的结果也会使频域分析很难定位到信号基频、2倍频等,进而限制了频域分析的覆盖面[6],会导致部分故障特性无法识别。 因此,笔者提出一种具有自适应功能的采样设计,基于高速模拟数字转换器(Analog-to-Digital Converter,ADC)和数字信号处理(Digital Signal Processing,DSP)平台,运用线性插值重采样方法, 进行高采样频率的FFT运算,实现设备的振动分析。
1 基本原理概述
1.1 FFT原理
设复数序列x(n)={x(0),x(1),…,x(N-1)},其离散傅里叶变换(DFT)X(k)为:
由式(1)可知,N点DFT需要做N2次复数运算。当N取值较大时,DFT需要大量的运算次数,实际应用中对计算资源和数据存储资源的要求很高[7]。

1.2 重采样原理
1.2.1 线性插值
线性插值是数学和计算机领域广泛使用的一种简单插值方法[8]。 对于已知点(x0,y0)和(x1,y1),区间[x0,x1]内x对应的函数值为:

考虑到采样频率足够高时两个采样点间隔较小,线性插值已经可以满足设计要求;加之其他复杂插值方法对内存空间与硬件计算性能要求较高,而线性插值算法具有简单特性,故采用线性插值方法进行重采样。
1.2.2 重采样
重采样的目的是在N′个实际采样点数中,通过线性插值方法,等时间间隔抽取N点(本项目以N取2 048为例),以顺利进行FFT运算[9]。 在总采样时间不变的前提下, 重采样后采样点数改变,采样频率随之改变,并存在以下线性关系:

其中,fS为重采样后的采样频率,fS′为原始采样频率。
如果总采样时间改变, 则fS与fS′将不存在线性关系,导致fS不能被准确计算[9]。所以,重采样过程存在一个约束条件,即首尾两个数据点必须保留,以保证总采样时间不变。
数据点插值示意图如图1所示, 为满足约束条件,在每两点间插值2 046个,则总点数M=(N′-1)×2046+N′=2047N′-2046。第0点被保留,则剩余2047(N′-1)点,每(N′-1)点取最后1点,加上第0点则刚好抽取2 048点,且首尾两点均被保留。

图1 数据点插值示意图


图2 插值后总点数示意图
对于i=0~2047,有下式成立:
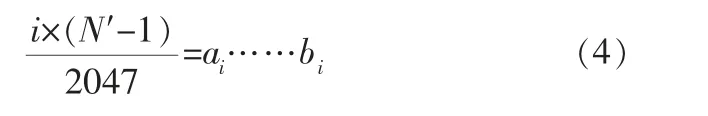
得到商ai余bi,那么线性插值点位置是实际采样点ai与ai+1之间的第bi点, 根据线性插值公式,有:

2 自适应采样实现
2.1 被测对象说明
如图3所示, 振动信号①由旋转机械的振动传感器产生[10],键相信号②由键相传感器产生并经电路调理所得[11],其一个脉冲代表机械转轴转动一周,采样时由DSP捕获键相信号②,在其下降沿③对振动信号①进行采样,经过相应周期后在其下降沿③结束采样,其中每两个相邻下降沿之间即1个整周期④。 键相信号的作用:一是DSP对其进行捕获,计算转轴转速;二是DSP在键相信号下降沿开始采样并在相应周期后的下降沿结束采样,保证振动信号的整周期采样[12]。
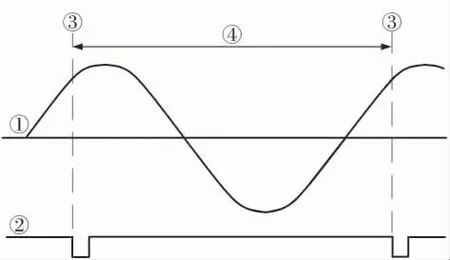
图3 振动信号采样示意图
2.2 数采硬件拓扑
笔者设计的数采硬件平台主要由高速ADC与DSP构成。 为了保证较高的采样频率与采样精度,设计选用采样率达百kSPS的∑-ΔADC[13]。FFT运算要求数据点数为2的整数次幂, 点数越多频谱分析的分辨率越小,精度就越高。 本项目取常见的2 048点(16位),则一组原始数据与重采样后数据将占用十几KB内存,考虑到RAM对DSP价格影响较大 (以TI公司C2000系列为例,RAM增加1倍价格也大致增加1倍), 因此选取几十KB RAM即可。由于ADC采样频率较高,则要求后级DSP有较强的运算能力,以避免数据处理慢而导致前后级不匹配的问题,因此选用计算速率达到百MIPS的DSP[14]。
基于DSP的振动信号自适应数采硬件拓扑如图4所示,振动信号由传感器产生,经卡件调理电路后由ADC进行模数转化, 最后由DSP根据键相信号进行采样,并做数据处理。

图4 数采硬件拓扑示意图
2.3 采样方案
DSP内部采样流程如图5所示。 首先,DSP对键相信号进行捕获,计算信号频率,根据预设分段频率确定采样周期数n。 然后,DSP在键相信号下降沿对振动数字信号整周期采样,并对采样数据进行线性插值重采样,将得到的2 048个数据点进行FFT运算。 最后,计算得到振动信号0.5倍频、基频与2倍频的幅值,根据工业应用要求,幅值精度须达到±1%。

图5 振动信号采样流程示意图
2.3.1 采样周期数确定
采样数据经FFT运算后, 得到相应频率点的幅值,将其描绘成图(即幅频谱图)。 频域分析精度主要取决于两个方面: 一是FFT运算后目标频率是否被准确定位; 二是频谱分辨率是否足够高。
设ADC硬件采样频率为fADC、 信号基频为fB,则实际采样数据点N′的计算式为:

从N′个实际采样点中插值抽取N点, 则真实信号采样频率fS的计算式为:

由此可得FFT频谱分辨率为:

那么,对于频谱任一点Z(Z≤N,且Z为整数),其频率fZ的计算式为:

因此,频谱分辨率只与fB和n有关。 如果n取整数,那么信号基频一定能被准确定位。 至于分辨率,由于最小需要分析到信号0.5倍频,则n≥2即可。所以,为了准确定位到信号的0.5倍频、基频与2倍频,取n≥2且n为整数即可。
由上述分析可知,n取值越大,频谱分辨率越小,分析结果越精确,但N′也越多。 由于DSP的内存所限,N′不能无限增加。 由于实际内存为几十KB且抽取点数为2 048,因此将N′约束在8 192点以内即可。ADC最大采样频率设定为62.5 kHz,根据式(7)可得信号频率与采样周期数的关系,详见表1。
从表1可以看出,当信号频率不断减小,为了保证N′在约束条件以内,n也不断减小;但n取最小值2后信号频率仍不断减小,此时已不能通过减小n的值来控制N′。 为了在低速时仍然能够进行采样并准确分析,只能通过降低硬件采样频率fADC来满足约束条件。 对工业应用的调研结果显示,单事件转速在60 r/min以下一般不需要监测振动状态,故将最小频率定在1 Hz。 在中高转速下,实际采样点数在4 000~8 000;在低转速下,实际采样点数在3 906~7 812,都能满足N′的约束条件。

表1 信号频率与采样周期数对应表
DSP捕获到键相信号并计算信号频率后,与表1数据进行对比,从而确定采样周期数,根据键相信号,下降沿采样n个周期。
2.3.2 采样频率分析
根据香农定理, 采样频率必须不小于2倍的信号所包含的最大频率,才能包含原信号的所有真实信息[15]。 若采样频率不满足该约束条件,原始信息不能被完全采集,那么频域分析结果将存在较大误差,因此采样频率对本设计的精度有重大影响,根据式(8)将表1数据代入可得信号频率与采样频率对应表(表2)。

表2 信号频率与采样频率对应表kHz
本设计频域分析范围最大到信号的2倍频,即分析的最大频率是信号频率的2倍。 根据香农采样定理和表2可知,采样频率远大于4倍的信号频率,所以采样后的信号不会失真,保证频域分析得到的结果包含了所有真实信息。
3 仿真验证
3.1 采样方法对比验证
本测试是在DSP内部用纯算法模拟完成的。DSP生成仿真振动信号, 采用不同方法对仿真振动信号进行采样并进行FFT运算, 对比其频域分析的频率与幅值精度。
采用以下3种不同的采样方法:
a. 延长采样时间——定点采样8 192点做FFT运算;
b. 补零——实际采样点数与本设计相同,对采样点进行补零,使采样点数达到2的整数次幂;
c. 本设计方法——多周期采样,线性插值重采样。
为了对比信号的0.5倍频、基频与2倍频,仿真信号包含3种成比例的频率。 测试对比3种方法频域分析后的频率与幅值精度, 详见表3, 可以看出,定点数采样与补零方法都不能准确定位到信号0.5倍频、基频与2倍频,频域分析得到的频率与信号存在一定偏差,且该偏差随信号频率变化而变化,不能控制在一定范围内。 频率的偏差导致幅值存在较大误差, 仅3次测试最大相对误差即高达-36%(仿真信号2, 补零方法, 基频幅值,(0.1591-0.25)/0.25=-36.36%)。 而本设计完全可以准确定位,频率不存在偏差,幅值的相对误差均在±0.3%,相较于前两种方法有明显改善。

表3 模拟振动信号频域分析结果对比
为了使结果更直观, 将运算数据在MATLAB以频谱图形式呈现[16],如图6所示,其中仿真信号为y =0.25sin (2π ×150 ×t) +sin (2π ×300 ×t) +0.25sin(2π×600×t)。 从图6可以看出,定点数采样方法和补零方法的频谱图存在其他频率分量的干扰,定点数采样频谱图的目标频率附近分量有较大幅值,补零频谱图则分布着较多起伏的频率分量; 本设计则基本消除了干扰频率的影响,频谱图呈现出目标频率幅值大、干扰频率幅值极小的理想图像。

图6 3种方法运算数据在MATLAB的频谱图
综上,相比于目前常见的方法,本设计有着明显的优势,极大提升了振动信号频域分析的精度。
3.2 采样精度验证
为了验证本设计分析结果的精度,分析仿真振动信号,得到相应频率与幅值的分析结果(表4),可以看出,本设计频率不存在误差,0.5倍频、基频与2倍频幅值最大相对误差分别为全量程的±0.03%、±0.10%与±0.11%,相对误差在本设计±0.3%精度之内。

表4 模拟振动信号频域分析结果

(续表4)
综上,本设计得到的频率与幅值精度均达到了设计目标。
4 结束语
笔者提出的技术方案主要针对大型旋转机械设备振动信号的采样与分析,在目前常用采样方法精度不高的背景下,采用基于线性插值重采样的自适应采样方案,在保持高采样频率的前提下,有效控制实际采样点数,无需占用太多硬件内存,实现了基于硬件平台的频域分析。 此外,本设计可准确定位到信号0.5倍频、基频与2倍频,使FFT运算后的结果误差最小。 仿真结果证实了本设计能够进行复杂信号的采样与分析,且精度相对于常见方法有显著提升, 满足工业应用需求。本设计可应用于监测旋转设备的振动状态,为旋转设备的高精度振动分析提供技术参考。

