采用欧式形态距离的负荷曲线近邻传播聚类方法

党倩,崔阿军,尚闻博,杨波,卫祥

(1.国网甘肃省电力公司信息通信公司,730050,兰州;2.国网甘肃省电力公司,730000,兰州)

近年来,中国智能电网的建设大力推进,智能电表的大量普及使用户用电数据的收集变得简单易行,更细粒度的用电负荷数据保证了供需交互的稳定性[1]。然而,海量信息的涌入意味着电力数据信息的冗余化与杂乱化。因此,如何运用数据挖掘技术,从用电数据中提取有效信息,分析用户用电模式,为电力决策提供参考,已被认为是电网领域的重要研究内容[2]。

电力负荷曲线聚类是电力数据挖掘中的常见技术,其目的是提取用户用电负荷曲线的分布特征,找出其中用户行为的相似点,进而归类分析用户用电模式[3]。目前,各类聚类分析技术方法已被应用于电力负荷聚类中,包含基于划分的聚类方法[4-5]、层次聚类方法[6]、基于图的聚类方法[7]等。

相似度量方法决定了聚类方法对于负荷曲线变化特征的敏感度,是影响聚类质量的重要指标[8]。主流方法大多关注于两条曲线相同采样点的负荷差异,最常见的方法为欧氏距离,通过计算相同采样点之间的距离均值,判断曲线相似程度。为了改善聚类质量:卜凡鹏等采用双层聚类的方式,外层结合皮尔森系数,内层使用欧氏距离,能够更细粒度地控制聚类结果[9];徐胜蓝等将欧氏距离与余弦相似距离结合,提出双尺度相似谱聚类集成方法,得到较好的效果[10];冯志颖等引入推土机距离,结合欧氏距离从横纵向两方面分析负荷曲线,可用于检测异常用电[11];李阳等使用差分算法及分位数提取负荷曲线斜率变化特征,根据对应时间点特征值是否相同进行归类,忽略了负荷曲线的位移变化特征[12]。虽然部分方法将两种相似度量方法行结合,实现不同方法优势的互补,但这类相同采样点之间点对点匹配的方法只能观察到负荷曲线之间整体的差异性,而忽略了用户用电的时间差异,随着负荷采样频率的提高,这类方法所能表达的信息将更加有限。针对这些问题,Teeraratkul等将动态时间弯曲距离(DTW)引入负荷聚类,实现了对曲线的动态匹配,但未能解决方法时间开销过大的问题[13]。

目前负荷聚类的度量方法主要有以下不足:①多数方法仅考虑负荷曲线相同采样点的数值差异,忽略了曲线的位移变化;②现有动态匹配方法计算开销过大,可能导致过度弯曲。

针对现有研究的局限性,本文提出了一种采用欧式形态距离的负荷曲线近邻传播(AP)聚类方法EMD-AP。将用电负荷曲线重表达为离散曲线形态变化特征,通过基于模式匹配距离的最长公共子序列(LCS)算法衡量不同特征序列的差异性,结合欧氏距离构造兼顾负荷曲线动态变化特征以及整体分布特征的相似度度量方法,使用熵权法对这2种距离方法进行权重赋值,采用AP聚类对不同用户负荷曲线进行区分。本文方法具有时间开销低和聚类准确性高等优点。

1 曲线相似性度量

1.1 负荷曲线特性分析

为了有效分辨不同负荷曲线之间的差异,本文从负荷曲线的整体分布特征和形态变化特征这2种特征来衡量负荷曲线之间的相似性。整体分布特征对应曲线相同时刻采样点之间的负荷差异度,反映了负荷曲线的整体相似度。形态变化特征对应曲线在采样时间内整体的形状变化特征的匹配程度,反映了形态变化情况。

1.2 曲线整体分布特征

欧氏距离是常见的点对点匹配方式,本文采用欧氏距离来度量负荷曲线的整体分布特征。给定2个等长用电负荷曲线X=[x1,x2,,xn]和Y=[y1,y2,,yn],X和Y之间的欧氏距离定义为

(1)

1.3 曲线形态变化特征

1.3.1 曲线形态变化特征提取 用电负荷曲线反映了用户在不同时刻的用电量,其实质是用户一系列用电行为的叠加。因此,本小节将用户用电负荷曲线转换为描述用户在不同时刻用电行为的特征序列。为了度量不同用户用电行为特征的差异性(同时忽略不同用户用电量级存在的差异),本文基于不同用户在每一时刻的用电量与用电最小负荷的差值,并且结合分位数对其用电特征进行提取与统一性重表达,得到使用离散类属性表达的曲线形态变化特征序列。

首先,对于用电负荷曲线X=[x1,x2,,xn],获取其最大值xmax与最小值xmin,计算两者的差值记为xrange;然后,采用分位数刻画其数据分布特征,为了去除噪声扰动并保留更多有效信息[14],采用五分位数组合τ=(0.1,0.3,0.5,0.7,0.9)计算曲线形态变化特征序列Xd=[xd1,xd2,,xdn],公式为

(2)

式中:Q1,,Q5为对应的五分位数值,Qi=τixrange+xmin;ddi为负荷曲线X在第i时刻的负荷xi与曲线最小值xmin的差值。

图1为曲线形态变化特征提取图。可以看出:五分位法将负荷曲线转化为离散的形态变化特征序列,完整保留了负荷曲线的波动特征,同时消除了负荷曲线用电负荷量级之间的差异性。

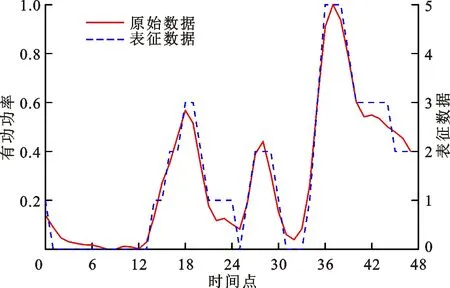
图1 负荷曲线形态变化特征提取图Fig.1 Morphological feature extraction of load curves

1.3.2 曲线形态变化特征度量 LCS是一种基于互相关的距离度量方法,用于寻找两条时序曲线的最长公共子序列,该方法能够抵抗一定程度的环境噪声和数据失真的情况,常用于模式匹配[15]。本文通过特征提取的方式将原始用户每一时刻的用电数据统一性重表达为仅由6种离散型类属性组成的曲线形态变化特征序列,消除了原始数值型数据之间存在的量级间差异。因此,可以提取出不同特征序列之间的公共子序列,并基于序列的长度来度量用户用电行为之间的相似性。

为了最大程度保留曲线的有效信息,本文对曲线进行等时间分辨率的形态重表达,使用模式匹配距离衡量用电行为特征的差异性。

模式匹配距离计算式为

(3)

对于给定的特征序列X=[x1,x2,,xm]和Y=[y1,y2,,yn],构建距离矩阵D∈Rm×n,矩阵元素di,j代表序列X的子序列Xi与序列Y的子序列Yj最大公共子序列的长度。采用动态规划算法求解其最长公共子序列,动态规划算法通常以从部分到整体的顺序进行解决,后一状态的结果往往由前一状态决定。对于矩阵中任意元素di,j需满足:①当dmode(xi,yj)=0时,公共子序列长度即为di,j=di-1,j-1+1;②当dmode(xi,yj)=1时,di,j为di-1,j和di,j-1的最大值;③为合理限制两条负荷曲线特征序列之间的匹配关系,使用阈值参数ε控制序列之间参数匹配的窗口尺寸,即di,j中下标i和j的距离需要小于ε。最终,两条特征序列之间的最长公共子序列长度即为dn,m。

改进LCS算法计算方式为

fLCS(X,Y)=

(4)

式中:m和n分别代表两条负荷曲线X和Y的长度,本文实验中m=n;阈值参数ε的取值范围为[0,m]。ε=0时,LCS算法退化为对两条曲线对应时间点的元素进行比较,算法时间复杂度为O(n);ε=m时,LCS算法为基于动态规划的LCS算法,算法时间复杂度为O(n2)。本文数据集中,每天包含48个采样点,假设同一类用电用户对于电气设备的使用最多存在2 h的偏差[13],即本文中阈值参数ε设为4。

不同时间序列之间的形态距离为

Dmd(X,Y)=len(Xd)-fLCS(Xd,Yd)

(5)

式中:Dmd表示两条用电行为序列之间的形态距离;len(Xd)为曲线形态特征序列Xd的长度,即Dmd取值范围为[0,len(Xd)]。Dmd越小说明2条时序曲线的公共特征子序列越长,曲线的形态变化特征越相似。

2 采用欧式形态距离的AP聚类方法

2.1 引入形态距离的必要性

对于负荷曲线,在衡量其相似性时需要考虑到位移变化、尺度变化和噪声变化特性,当负荷曲线发生这些变化后,相似度保持不变[16]。

传统采用欧氏距离的相似度量方法,仅考虑了两条负荷曲线相同时刻点之间的用电负荷差异,将导致聚类方法容易对具有位移变化的负荷曲线进行误匹配,造成聚类偏差。DTW能够对序列进行延展或压缩,达到识别曲线位移变化的目的。但是,这类方法通常是基于两点之间的欧式距离,对于用电模式相同但是进行了一定尺度变化的用户也很难做到精确分类,而且时间开销大。

由1.3小节可知,本文形态距离度量方法的特征在于:①相比欧氏距离,形态距离通过动态规划的方法,可以实现具有位移变化的曲线元素之间的匹配,保证了对曲线整体动态特性的学习,适用于2条曲线之间存在一定的时移偏差或者两条曲线负荷峰值窗口大小不一致的情形;②相比DTW,形态距离根据负荷曲线的负荷波动提取原始曲线的形态变化特征,在进行特征匹配的时候使用模式匹配距离,能有效忽略曲线的尺度变化,对曲线的负荷值不敏感,更适用于2条曲线形态相似但距离相近的情形。同时,在计算成本上,本文所提方法与DTW方法在不考虑阈值参数设定的情况下,时间复杂度均为O(n2),但是形态距离将曲线数值数据转换为定性数据,使用异同的思想衡量曲线形态差异,每次匹配只需要一次判等操作,计算过程简单,具体执行时间远小于DTW的。图2为形态相近但有位移变化的负荷曲线。

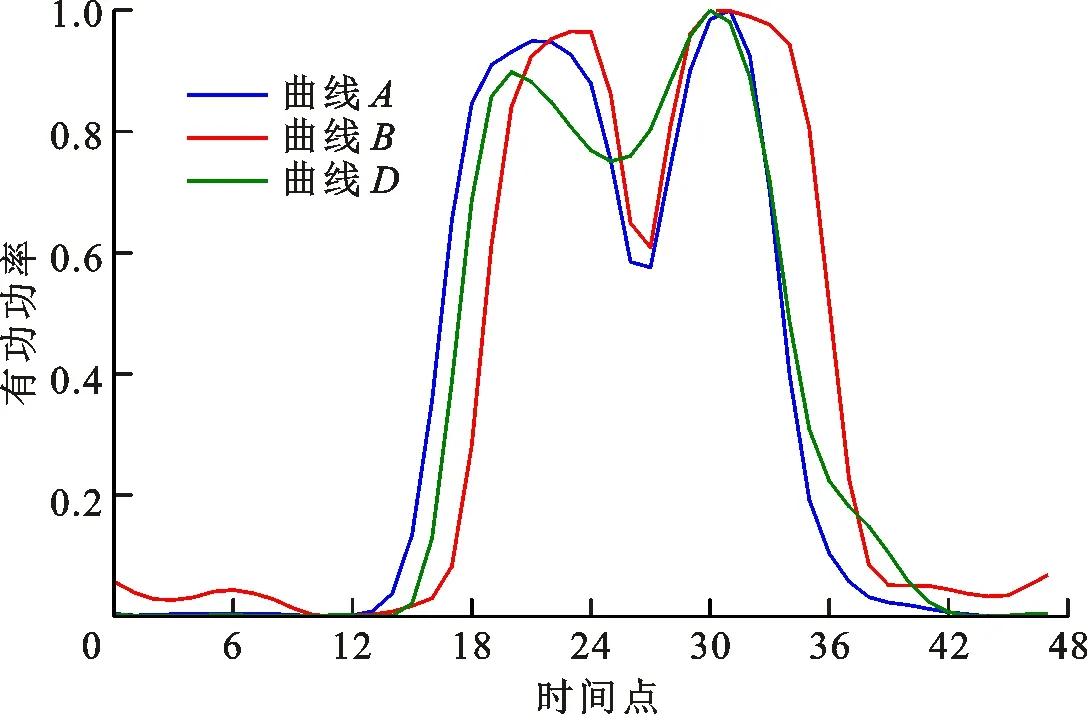
图2 负荷曲线形态特征对比Fig.2 Morphological feature comparison of load curves

由图2可以看出:3条曲线均属于双峰型负荷曲线,负荷曲线A和B形态更加相近,但是曲线A相对于曲线B有3个采样点的位移变化,曲线A和D距离更近但是形态差异更大。分别使用3种相似度量方式计算3类曲线的相似性。首先,采用欧氏距离计算,得到Ded(A,B)=1.368 9,Ded(A,D)=0.622 2。可以看出,如果仅使用欧氏距离作为曲线相似度的度量方式,那么对于这类出现位移变化的曲线识别效果较差。接着,采用DTW距离计算,得到Ddtw(A,B)=0.083 1,Ddtw(A,D)=0.102 4。采用形态距离进行计算,得到Dmd(A,B)=5,Dmd(A,D)=10。可以看出,DTW方法和形态距离方法均能得到曲线B与曲线A相似度更高的结论,更符合实际情况。

2.2 欧式形态距离描述

欧氏距离是一种基于点对点的曲线相似性度量方法,通过计算负荷曲线对应时间点之间的距离平均值获得曲线的相似度特征,能有效识别曲线的整体分布特征。形态距离方法通过对原始用电曲线进行离散属性表示,然后与基于LCS的动态特征匹配,得到曲线的特征匹配度,能有效度量曲线的形态变化特征以及相应的趋势匹配信息。

本文综合考虑曲线形态的整体分布特征和曲线的波动特征,构造一种负荷曲线双尺度相似性度量——欧氏形态距离,计算式为

Demd(X,Y)=αDmd(X,Y)+βrm,eDed(X,Y)

(6)

式中:Demd(X,Y)为负荷曲线X和Y之间的欧式形态距离;α和β分别为相似度矩阵的权重系数,为保证权重参数的客观性,使用改进熵权法[17]进行赋值;rm,e为形态距离与欧氏距离的比值系数,考虑到不同度量方法取值范围的不同,使用比例系数rm,e实现两种方法取值范围的统一,计算式为

(7)

2.3 聚类质量评价

2.3.1 内部评价指标 聚类内部评价指标一般用于对无标签数据聚类质量的评价,要求数据具有较小的类内聚合度和较大的类间差异度。本文采用在电力数据集有较好聚类评价效果的DB指标[18]。

DB指标能综合计及簇内的集聚度和簇间的分离度,计算式为

(8)

(9)

式中:d(Xk)和d(Xj)分别为簇Ck和簇Cj中样本点与样本中心的平均欧氏距离,表示一个簇内样本间的聚合度;d(Ck,Cj)为簇Ck和簇Cj中样本中心之间的平均欧氏距离,表示两个类簇之间的分离度。

考虑到传统基于欧氏距离的IDB已不能对本文方法进行准确评价,提出基于欧式形态距离的修正指标MDB,计算式为

(10)

式中:demd(Xk)和demd(Xj)为簇Ck和簇Cj中样本点与样本中心的平均欧氏形态距离;demd(Ck,Cj)为簇Ck和簇Cj样本中心之间的平均欧氏形态距离。

IDB和IMDB都是将两簇之间的类内聚合度和类间分离度做比,因此数值越低代表聚类质量越高。在选择最优聚类数时一般寻找其极小值点。

2.3.2 外部评价指标 外部评价指标用于在样本真实标签已知的情况下,将样本真实标签及聚类结果进行对比,以评估聚类有效性。选择调整兰德系数(AR)指标和FM指标共同评价各方法聚类结果的有效性。

(1)AR指标。AR指标是一种常见的聚类外部评价指标,通过计算在真实标签和聚类结果中被分配在相同或不同类簇的样本对数来评价聚类有效性,计算式为

(11)

(12)

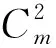
FM指标为成对的准确率和召回率的几何平均值,具体定义为

(13)

式中:NTP为在真实标签与聚类结果中均被归为同一类的样本对数量;NFN为在预测标签组中不属于同一簇而属于真实标签组的样本对数量;NFP为在预测标签组中属于同一簇而不属于真实标签组的样本对数量。

IAR取值范围为[-1,1],IFM取值范围为[0,1],数值越大表示聚类结果越贴近真实情况,取值为1时表明聚类结果与真实标签一致。

2.4 近邻传播聚类方法介绍

AP聚类方法认为所有样本都有成为聚类中心的可能性,它通过选举的方式选拔出一组高质量的样本作为聚类中心。相比于传统的聚类方法,AP聚类方法通过控制参考度调节聚类数[19],并且具有更高的稳定性[20]。本文引入欧式形态距离对负荷曲线相似度进行度量,提升聚类效果。

2.4.1 相似度矩阵的构建 AP聚类方法以成对样本之间相似度距离构成的相似性矩阵S作为输入,矩阵元素S(i,j)一般为序列X和Y之间欧氏距离的相反数。本文S(i,j)=-Demd(X,Y)。S(i,j)越大则序列X和Y越相似。

除了相似度量方法的设定,AP聚类方法还通过参考度p和阻尼系数λ控制方法的聚类效果。参考度p对应为相似度矩阵的对角线元素S(i,i),可以通过调节参考度p控制最终聚类结果的粒度,参考度越大则聚类数越少。本文p的初始值取相似度矩阵的最小值,后续通过聚类评价指标进行调节。为了避免在聚类过程中出现参数振荡无法收敛的情况,本文将λ的默认值设定为0.9。

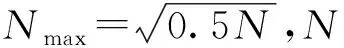
图3 本文方法流程Fig.3 Flow chart of proposed method

步骤1数据预处理。首先,对原始数据进行数据清洗,去除全0、全天负荷不变以及缺失超出10%的负荷曲线,取8月工作日用电负荷曲线并取均值,作为典型日用电负荷曲线。为避免异常负荷值对重表达效果的影响,使用高斯滤波对曲线进行平滑处理,并进行极差标准化。

步骤2参数初始化。设定AP聚类的参考度p、阻尼系数λ和最大迭代数,初始化归属度矩阵A和吸引度矩阵R。根据式(1)计算基于欧氏距离的相似度矩阵,根据式(2)～(5)计算形态距离相似度矩阵,并根据改进熵权法计算不同相似度矩阵权重系数,根据式(14)完成对相似度矩阵的初始化。

步骤3基于欧式形态距离的AP聚类结果。更新吸引度矩阵和归属度矩阵,直至矩阵稳定或达到最大迭代数t。如果聚类数达到Nmax,则进入步骤4中。否则,调节p,重复执行步骤3。

步骤4确定最优聚类结果。根据聚类结果,计算有效性指标,选择IDB最小时的聚类结果作为最优。

3 实验与分析

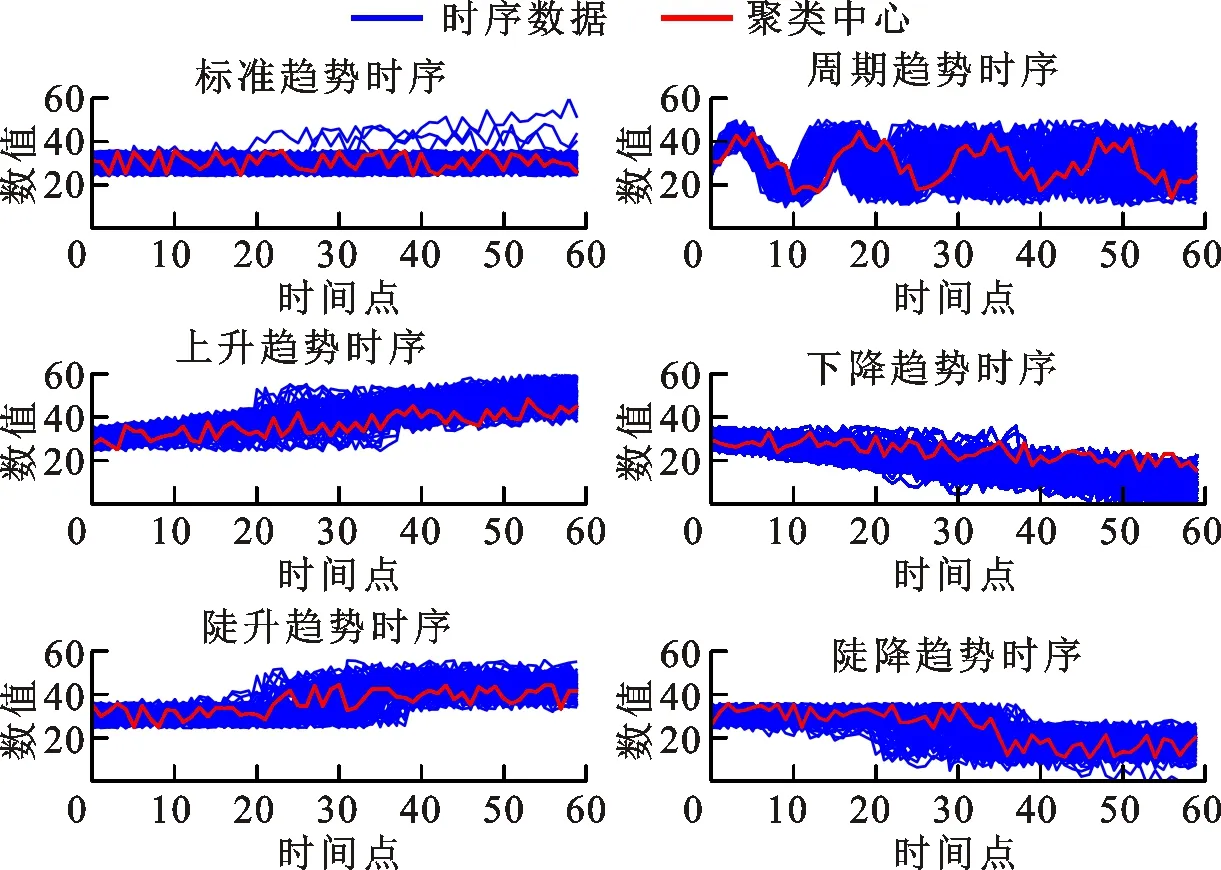
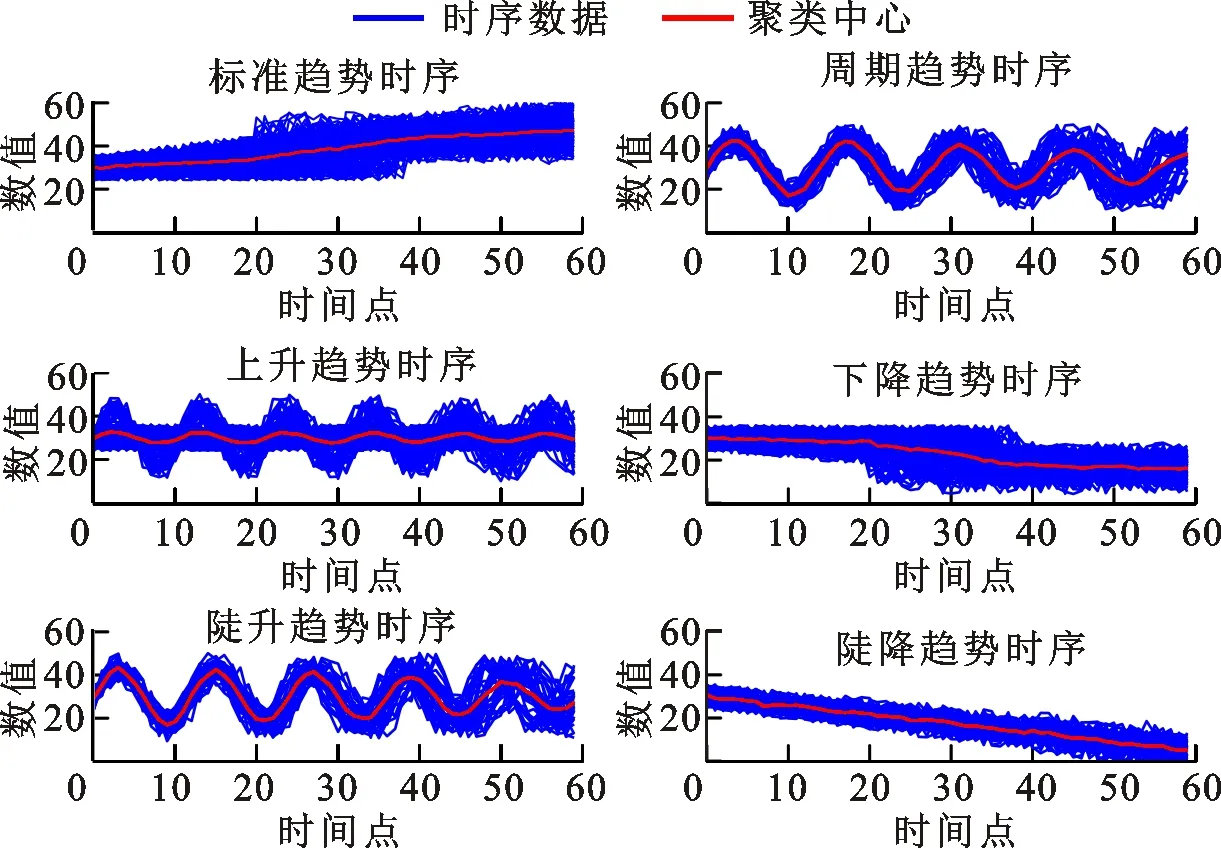
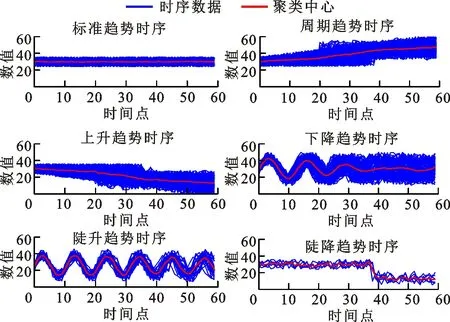
本文实验数据集包含两个部分。数据集1为UCI网站提供的一套标准合成时间序列数据集,如图4所示。该数据集包含600个有标签时间序列数据,分为6种不同的变化趋势,每种变化趋势包含100条时序曲线,使用数据集1验证本文方法的有效性。数据集2为爱尔兰居民用电实测数据。

(a)标准趋势 (b)周期趋势

(c)上升趋势 (d)下降趋势

(e)陡升趋势 (f)陡降趋势图4 标准合成时间序列集Fig.4 Standard synthetic control chart time series

本文算例均在一台Win10操作系统64 bit的计算机上完成,其配置为Intel(R) Core(TM) i7-6700 CPU @3.4 GHz,编程语言为Python。

3.1 形态距离有效性验证

为了验证形态距离用于衡量负荷曲线相似度的有效性,使用基于形态距离的AP聚类方法对数据集1进行聚类分析。由于数据集1时序曲线长度为60,设置阈值参数ε为6。AP聚类方法通过参考度参数的设置来控制聚类数,该参数一般设为相似度矩阵的最小值。本文设定p的初始值为矩阵元素最小值,再通过调节该参数将各方法的聚类数调整为6,在此情况下对各方法聚类效果进行比较。

采用欧氏距离方法(ED-AP)、形态相似距离方法(MSD-AP)[21]、快速动态弯曲距离方法(FastDTW-AP)[22]、动态弯曲距离方法(DTW-AP)、形态距离方法(MD-AP)以及本文欧氏形态距离方法(EMD-AP)的聚类结果如图5所示,实验中设定聚类数为6。

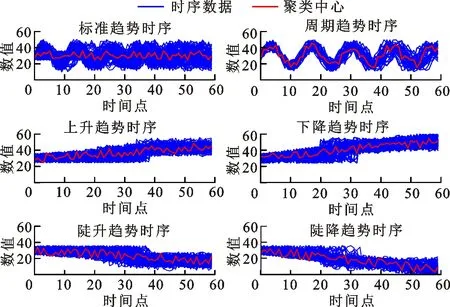
(a)欧氏距离方法

(b)形态相似距离方法

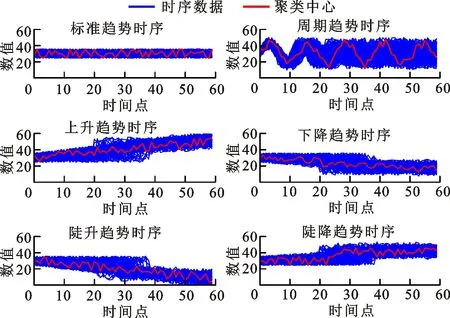
(c)快速动态弯曲距离方法

(d)动态弯曲距离方法

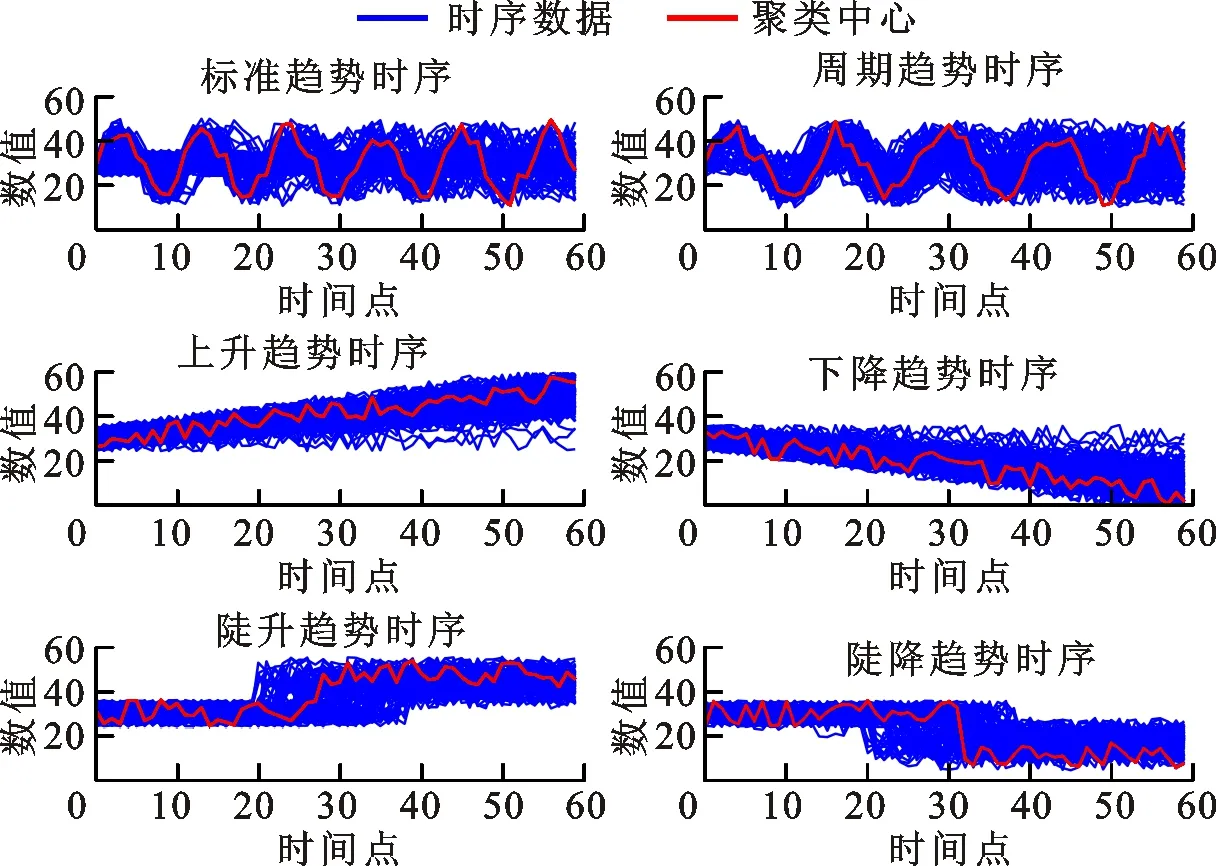
(e)形态距离方法

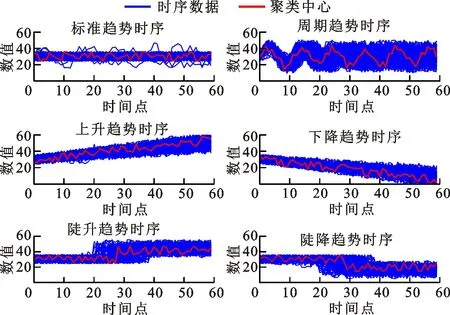
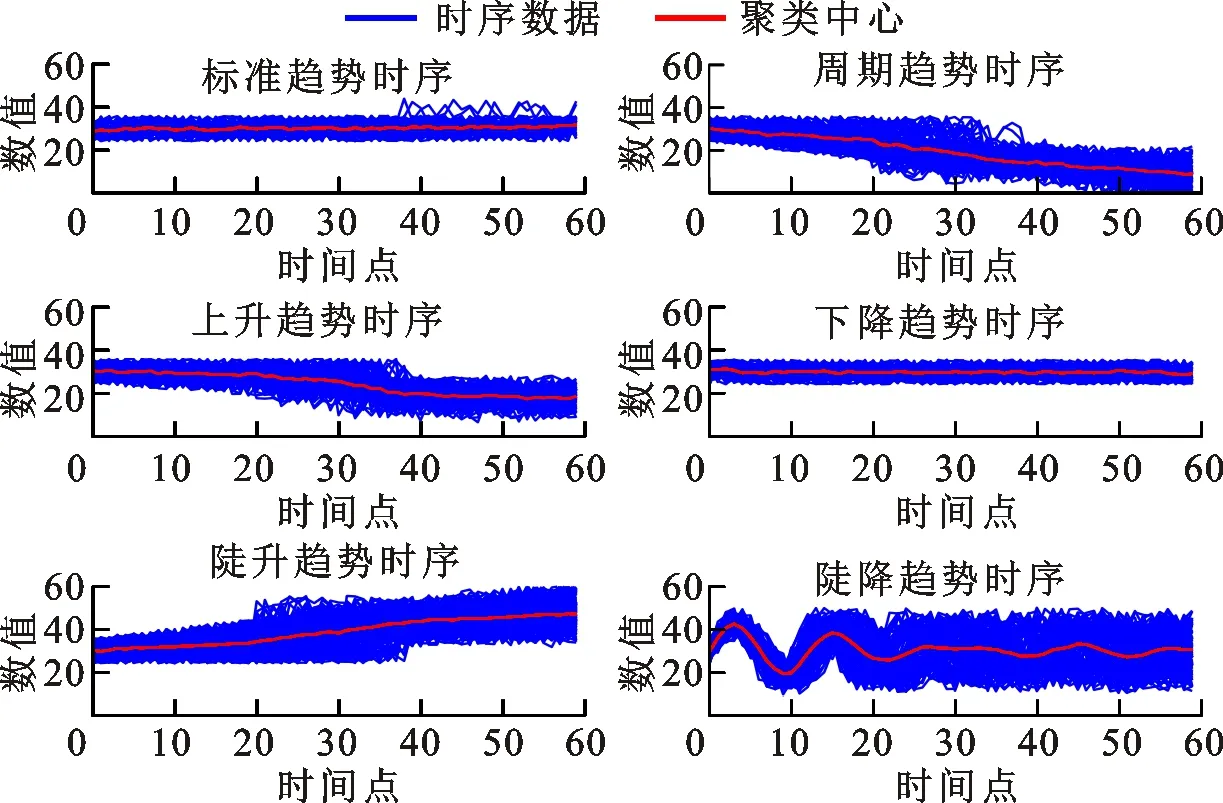
(f)本文欧氏形态距离方法图5 不同相似度度量方法聚类结果对比Fig.5 Clustering results of different similarity measures

由图5f可知:本文所提方法能够准确识别曲线整体的形态变化特征,然而对于第一类振荡变化和第二类周期性变化的时序曲线辨别能力较差。正如在2.1小节中对形态距离的分析,由于对原始用电数据进行了类属型转换,所以原始曲线的数值差异性会被忽略。周期性曲线和振荡变化曲线的差异主要在于点对点之间的距离以及变化的周期性。形态距离主要针对于形态变化的特征,忽略了点对点之间数值的差异性,因此对于周期性特征和一般性波动特征的辨识度不高。对比图5a、5b可以看出,形态距离在形态趋势变化方面的识别效果明显优于采用欧式距离和形态相似距离等方法,后两种方法均无法分辨时间序列的渐变趋势和陡变趋势,而本文方法在周期性数据和标准数据的辨别方面逊色于DTW。

为直观表示形态距离对数据集1的分类效果,本文给出了方法聚类前后簇的相同元素数。表1为使用形态距离对数据集1聚类的结果,表中,Vi代表在聚类结果中同一类曲线在各类簇Ui的实际聚类情况,每一类曲线均为100条。

表1 形态距离方法聚类结果Table 1 Results of morphological distance scheme

由表1可知,形态距离方法对于数据集1中后4类变化特征明显的曲线辨别能力较强。考虑到用户实际用电负荷曲线时段性特征以及峰谷特征明显,并且在周期特征方面的识别问题也可结合其他方法进行优化,因此形态距离方法适用于负荷聚类的场景。

3.2 欧式形态距离度量方法聚类效果验证

欧式形态距离综合考虑了曲线动态波动特征和整体分布特征,为检验该方法的有效性,将本文欧式形态距离的聚类结果与采用欧式距离、形态相似距离[21]、快速动态弯曲距离方法[22]、动态弯曲距离、形态距离的聚类结果就聚类质量及聚类效率进行综合比较。聚类质量通过外部评价指标IAR、IFM以及内部评价指标IDB、IMDB进行综合评价;聚类效率通过方法运行时相似度距离矩阵的计算时间TSCT、聚类时间和迭代数进行评估。为保证在数据集1上针对不同聚类方法聚类有效性指标均有统一的聚类质量评判标准,在3.2和3.3小节中聚类有效性内部评价指标IDB和IMDB的计算,选择各类簇的均值作为聚类中心,而在实测数据集上通过推举的聚类中心进行计算[22]。同时,提供数据集1的有效性指标帮助衡量聚类质量。

表2为不同相似度量方法聚类结果比较,可以得出结论如下。形态距离方法与传统的相似度量方法相比,在聚类准确度和精度方面都有一定的提升,而相似度矩阵计算时间也在可接受范围内,并且通过牺牲空间复杂度的情况下还可以对计算时间进行进一步优化。与基于FastDTW的计算方法和基于DTW的计算方法相比,形态距离方法大多数指标均优于FastDTW方法,在IAR上和DTW方法有4%左右的精度差距,同时IDB也高于DTW方法,这也符合3.1小节中针对实际聚类结果得出的结论。但是,形态距离在IMDB和TSCT方面明显优于DTW方法的,具有较低的时间开销。欧式形态距离方法在IAR上相对于欧氏距离方法和形态距离方法分别提高了43.8%、13.1%,同时IDB与标准集仅相差0.014 3。

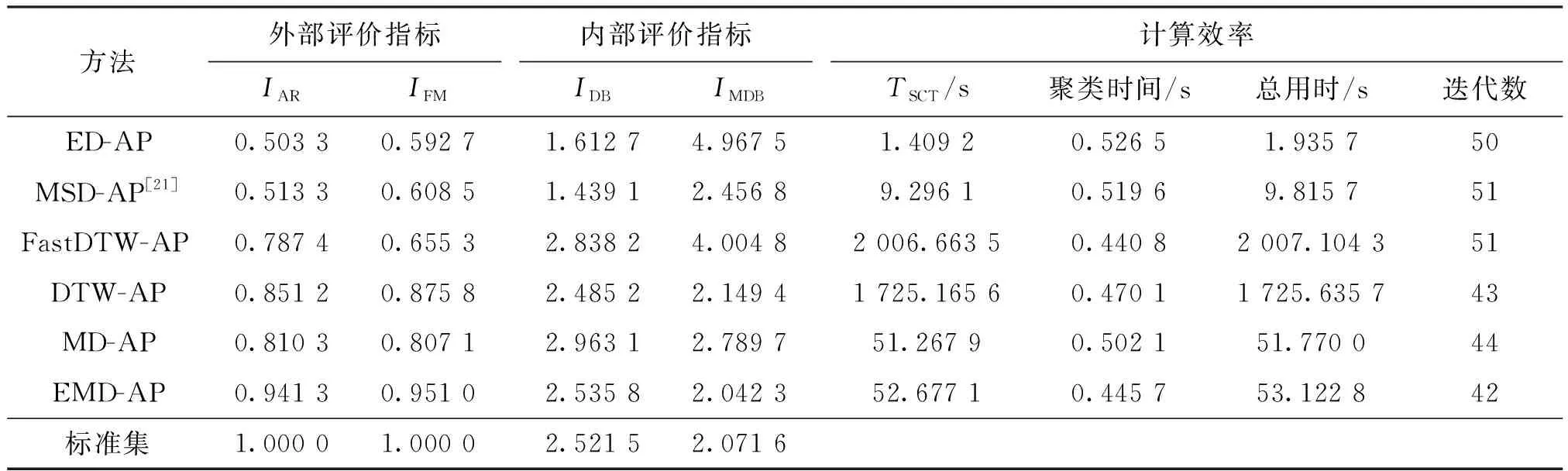
表2 不同相似度量方法聚类结果指标比较Table 2 Clustering results of different similarity measures

在加入曲线整体形态变化特征后,方法收敛性增强,迭代数有所减少。相比于基于FastDTW和基于DTW等两种基于动态弯曲距离的方法,本文方法在更低的时间开销下能实现更优聚类质量,并且得到了更高的分类准确率以及聚类紧凑度。由图5f可知:欧式形态距离方法能有效辨别这6类不同变化特征的曲线,6个类簇的分布情况非常接近标准集。对比FastDTW方法和DTW方法,欧式形态距离方法在聚类有效性和计算效率上均优于DTW方法,这也说明了采用阈值参数降低方法时间复杂度的有效性。

3.3 不同聚类方法聚类效果对比

采用基于DTW的K均值方法(DTW-KM)[13]、基于遗传算法的谱聚类方法(GA-NJW)[23]、K-medoids方法[24]以及凝聚层次聚类方法[24]进行对比。为避免数据预处理操作对聚类效果的影响,分别对这些方法在原数据集与高斯平滑滤波处理后的数据集上进行测试,选取两者效果更好的结果。实验中各方法聚类数均设为6,关键步骤或模型参数如下:在DTW-KM方法中,DTW的时间窗口长度与本文LCS方法一致,均设为6,K均值方法最大迭代次数为300;GA-NJW方法引用了原文的实验结果以作对比,并实现了文献中提出的NJW(M=11)方法;在K-medoids方法[24]中,本文分别设置最大迭代数为300、500和700进行实验,并最终设置最大迭代数为500。所有方法均完成了20次重复试验,取其最优。图6为部分聚类方法的聚类结果。

由图6可知:K-medoids方法对于前两类曲线的识别效果较差;层次聚类方法对于渐变趋势和陡降趋势的曲线识别效果较差;NJW和DTW-KM方法对于陡升趋势和上升趋势的数据识别效果较差。

表3为多种聚类方法聚类结果的比较结果。可以看出,本文方法在IFM和IAR上均具有最优的结果,说明了欧式形态距离方法最终聚类结果的准确度更高。在IDB上,欧式形态距离方法的聚类结果虽然大于K-medoids、 层次聚类以及NJW方法的,但是通过对比发现各类簇的分布情况更接近于原始数据集的。IMDB也具有相同的特点。因此,从多种方法的聚类结果进行分析,欧式形态聚类方法也具有较高的分类精度。

(a)K-medoids方法

(b)层次聚类方法

(c)DTW-KM方法

(d)NJW(M=11)方法图6 不同聚类方法聚类结果对比Fig.6 Clustering results of different clustering methods

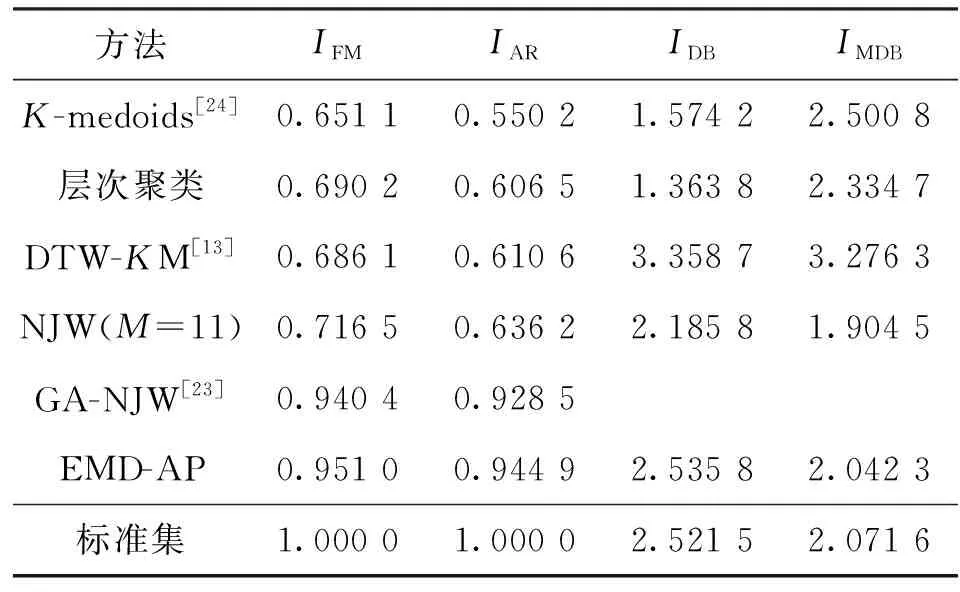
表3 各聚类方法指标对比Table 3 Clustering indexes comparison of different methods

3.4 稳定性分析

在实际基于负荷建模的过程中,方法聚类结果的稳定性与可复现性也是非常关键的因素。20次重复实验下的IFM如图7所示。

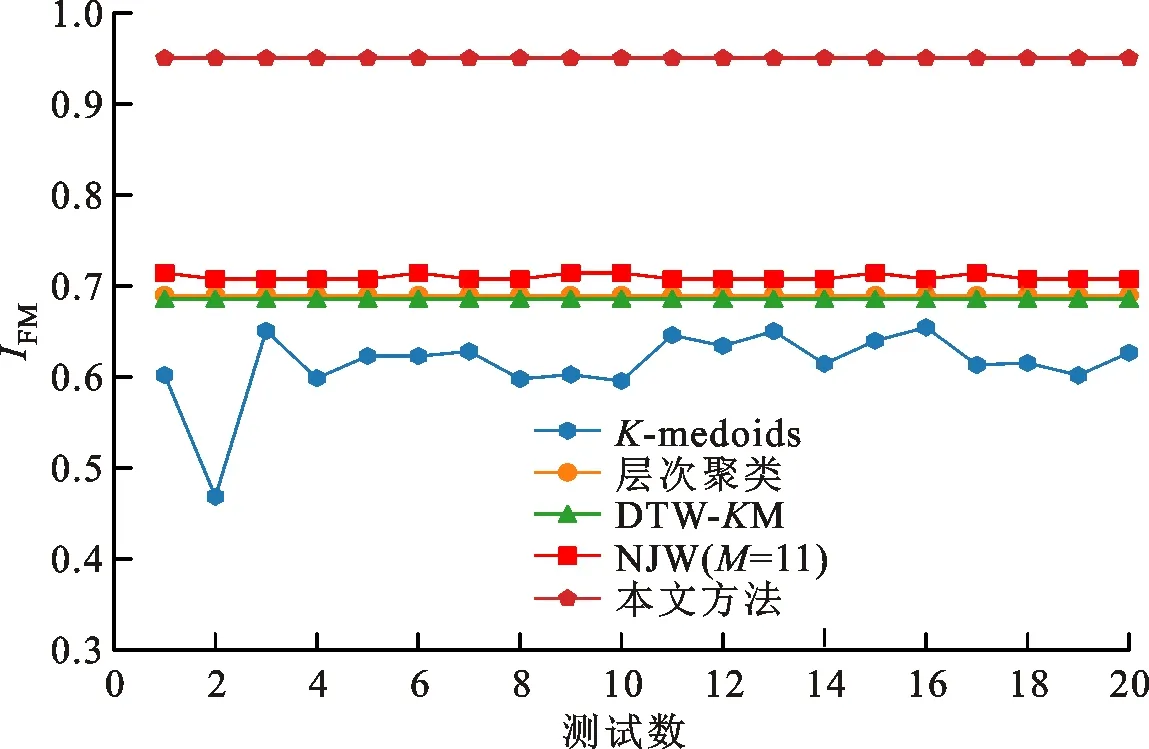
图7 不同方法聚类稳定性对比Fig.7 Comparison of stability for different methods

由图7可知:K-medoids方法20次聚类结果波动较大,且聚类质量较差;NJW方法较K-medoids方法稳定性更好,但也存在陷入局部最优解的情况;DTW-KM、层次聚类方法以及本文方法在多次实验的情况下均能保持稳定的聚类结果,但本文方法聚类效果明显优于前二者,证明了本文方法聚类结果的优越性以及稳定性。

3.5 实际负荷数据集测试

本小节数据来自于ISSDA网站发布的爱尔兰智能电表实际量测数据[25]。从中随机选取800名用户为实验对象,实验结果如图8所示。

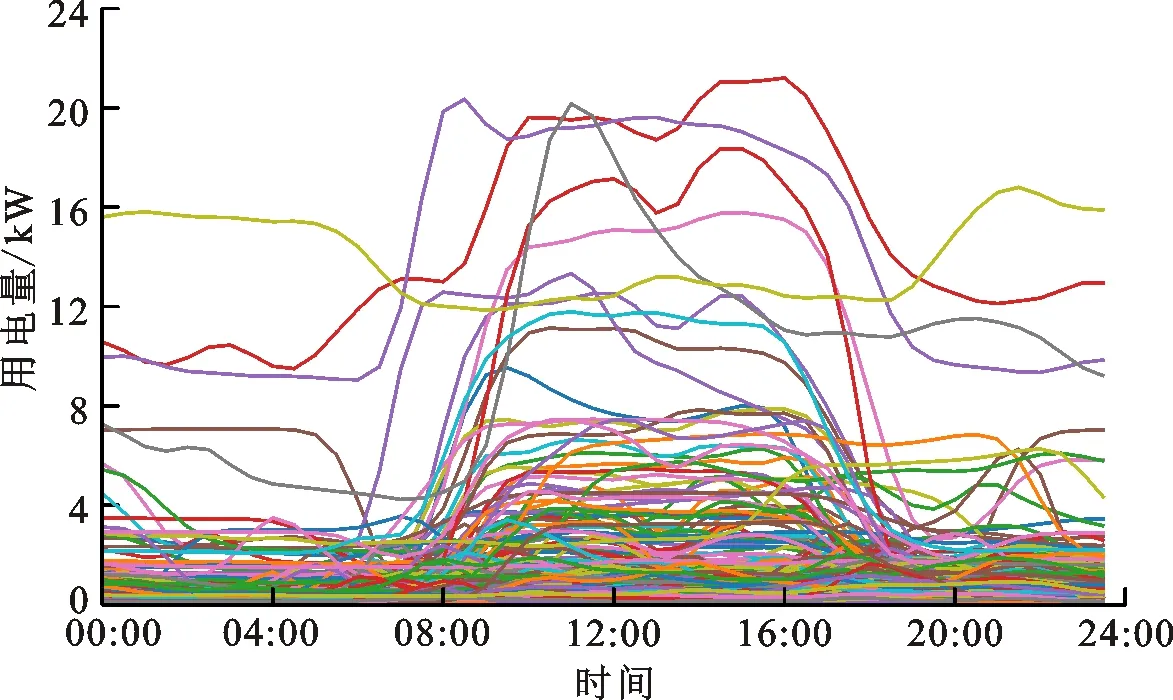
图8 800位电力用户用电实测数据Fig.8 Measured data of 800 power users

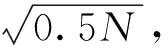
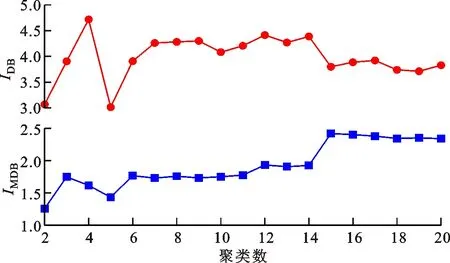
图9 聚类数与聚类有效性指标的变化关系Fig.9 Relationship between cluster number and cluster validity indexes

由图9可知:聚类数为5时,IDB明显下降并且出现最小值,因此选择最优聚类数为5;IMDB在聚类数为5时也出现极小值点,这也反映了将最优聚类数定为5的准确性和合理性。图10为聚类后的各类用户用电负荷曲线。

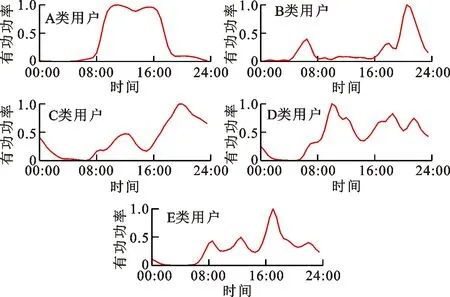
图10 电网实测数据聚类中心图Fig.10 Clustering center of measured data in power systems

由图10可知:不同类簇之间用电负荷曲线的形态差异较大,用户的用电特征明显;A类用户为典型的峰平型负荷,此类用户用电特征明显,08∶00-18∶00为工作时段,在工作时段内具有较高的用电负荷,在12∶00因为午休用电负荷有所下降,在非工作时段用电负荷骤降,这类用户可能为商业、工厂或办公楼等工作场所;B类用户在06∶00-21∶00出现用电高峰,其他时段用电量偏低,属于避峰型用户;C类用户在12∶00和21∶00出现用电高峰,属于双峰型用电用户;D类用户分别在10∶00、19∶00和21∶00有多次用电峰值出现,属于典型的三峰或多峰用户;E类用户在平时段用电平稳,而在18∶00出现用电高峰,可能属于上班族,白天在外工作,18∶00后回家,出现用电量峰值。

经本节分析可知,本文方法综合考虑了负荷曲线欧氏距离及形态距离,获得了考虑用能特性差异的归类结果,该归类结果说明了用户各种用电模式的分类情况,可用于为电力企业提供用户用电模式信息、电力负荷预测[26]以及制定能源规划策略等。同时,通过控制方法的阈值参数可以获取更精细化的分类结果,帮助电力企业推出个性化服务。

4 结 论

考虑到传统方法对于具有位移变化负荷曲线识别效果较差,本文提出了一种基于最长公共子序列的电力负荷曲线聚类方法,以模式匹配距离作为用户用电模式的差异度,将传统点对点距离计算简化为整数间的判等操作,有效降低了时间开销。相比于DTW方法,本文方法将时间开销从千秒级降低到了十秒级别,并且保留了对于陡变趋势以及渐变趋势这类相似变化特征的识别效果。考虑到方法在周期性曲线的识别方面具有一定的劣势,本文结合欧氏距离构造了一种兼顾负荷曲线的整体分布特征及局部动态变化特征的相似性度量——欧氏形态距离。算例证明:欧式形态距离方法具有较高的聚类精度,与多种经典方法相比,在聚类精度及聚类效率上均具有一定的优势,在实测电力数据集上提取的各类用电负荷曲线形态变化特征明显,可用于负荷预测、典型用电负荷提取、用户个性化服务及需求响应等领域。但是,本文所使用的AP聚类方法无法自动确定最优聚类数的遗留问题,有待在未来工作中进一步改善。