介电微杆在圆极化电场中的可控电旋转行为

在交流电动力学现象中,介电泳(DEP)、电旋转(ER)和电定向(EO)已被广泛用于描述和处理时变交流电场的粒子样本

。文献[4-5]提出在非均匀电场作用下粒子电极化的应力不平衡,因此正或负介电泳会使目标粒子在增加或减小的外加交变电场梯度中运动;文献[6-7]介绍了粒子在旋转电场驱动下的异步旋转运动和无相位变化的正弦稳态下非球形粒子的定向行为。文献[8-9]根据经典电偶极矩法和Maxwell应力张量法关于介电泳力的物理描述,通过实验观测以及粒子运动轨迹和拓扑形态的仿真结果,得出粒子在多电极阵列微流控芯片上运动的可行性和优势。文献[10]给出可极化粒子的电动行为在很大程度上取决于等效感应电偶极子,由粒子和电解质交界面处的介电特性突然跃变与外加电场相互作用而产生,且随粒子极化率变化而变化,粒子极化率包括介电常数和弯曲表面的表面电导率。

从当前的数学建模和仿真分析来看,粒子承受介电泳力作用的动力学研究仍然存在一些问题需要进一步解决,仅通过Maxwell-Wagner界面结构极化难以改变介电杆的旋转方式

。为了解决该问题并实现对介电杆旋转方向的灵活控制,本文提出在旋转电场中充分利用在结构化的悬浮微电极上方的诱导电荷电渗的优势。旋转诱导电荷电渗流场(ROT-ICEO)的动态流动停滞线(FSL)导致粒子始终在双层扩散频率周围以-10(°)/s数量级的角速度在原点沿共场方向旋转,与以相同角速度在标准电旋转的反场驱动方式形成良好的互补关系。

1 材料与方法

1.1 芯片结构

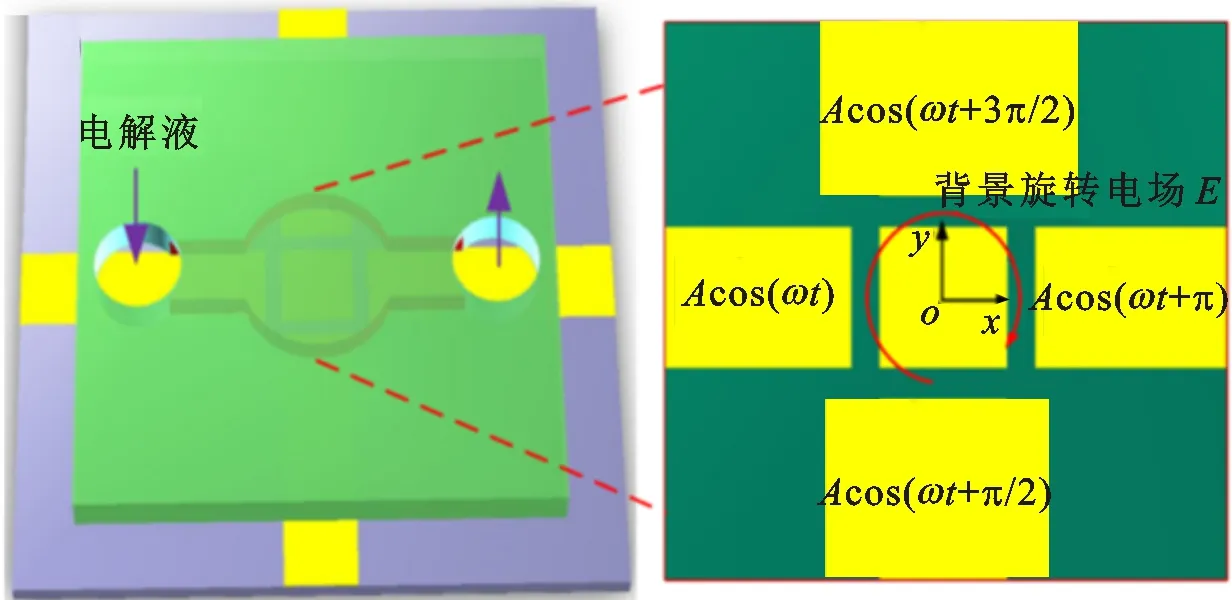
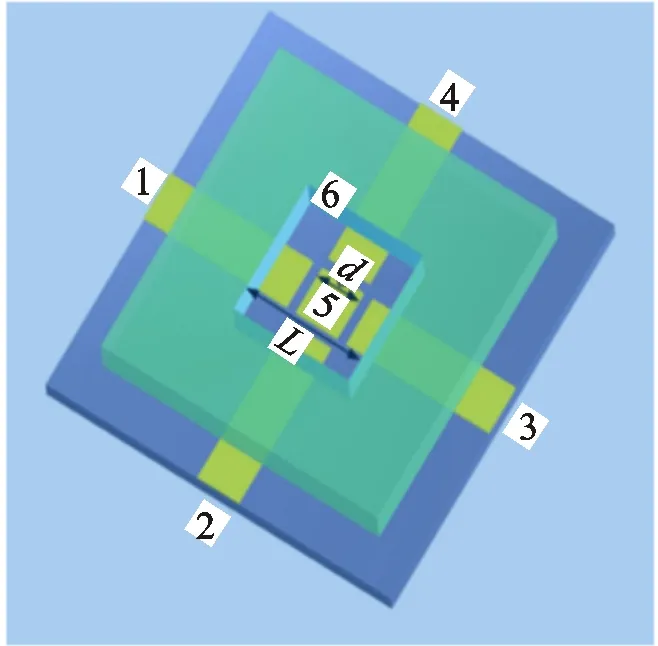
图1给出了微流控装置的模型结构,其中一个方形悬浮电极被4个条形驱动电极围绕,所有电极均由薄膜氧化铟锡(ITO)制成,并在由聚二甲基硅氧烷(PDMS)覆盖的玻璃基板模型上进行。相反极化电极的间距

为2 mm,方形ITO悬浮电极边长

为300 μm。一个500 μm高的PDMS通道与一对电解端口对准并与玻璃基板结合,形成所需的微流控芯片。旋转电场

(

)=Re(((2

)

+j(2

)

)e

j

)顺时针方向的传播几乎不受直流极限值中存在金属方形的影响,

为电压幅值,

=1～5 V,

=2 mm。由SU-8材料制成的介电微杆

的直径为11 μm,长度为47 μm,即

=23.5 μm,

=

=5.5 μm,介电微杆的介电常数

=10

,

为真空介电常数,KCL电解质水溶液的电导率设置为

=0.001 S/m,

足够低以满足稀溶液理论的极限

。通过使用多相函数发生器将相迁的交流电压源施加到4个ITO驱动电极上,以产生所需的粒子运动。粒子的瞬态运动可以通过光学显微镜进行观察,并可以通过高速CCD相机进行记录。

2.3在消毒供应中心内部,全员培训CICARE标准化沟通模式和沟通技巧。学会倾听,学会询问,学会解答。

1.2 表面传导对粒子极化率的影响

=4

(1+

)sin(

)(

4

)

(1)

式中:

为玻耳兹曼常数;

为环境温度;

为德拜长度;

为基元电荷;

为离子物种的价键;

为德拜层中紧实层的厚度;

为电动电势;

为电对流相对于电迁移对表面传导的贡献参数比

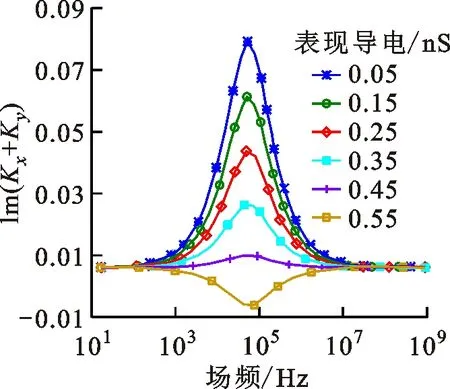
。由于杆体介电常数往往有限,在界面区域诱导的非均匀电动电位(zeta)导致表面电导的平均值约为1 nS的数量级。由于表面传导的作用,棒状粒子的体积电导特性在

、

、

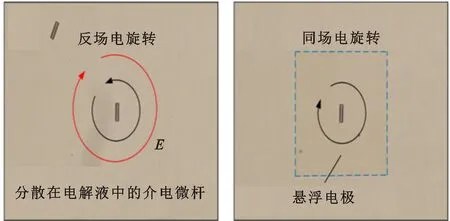
轴上呈各向异性。考虑到表面导电的影响,当前工作中所使用的SU-8介质微棒的电导特性如图2所示。在没有浮置电极的情况下,悬浮在电解质溶液中的介电微杆逆时针旋转,与电场的旋转方向相反。当悬浮微电极位于旋转场上方时,介电微杆在电场方向上表现出顺时针旋转的行为。

2 介电杆在电场中运动的结果与讨论

2.1 反场电旋转

在角频率

的外加电场

(

)中,

=2π

,

为线性电场频率,由于整个杆表面的极化率不连续,为了保证总电流密度法向分量的连续性,自由表面电荷和束缚表面电荷不得不被诱导在介电杆

电解质界面上。虽然界面诱导净电荷在相同的外加电场作用下,边界表面感应的双极性电荷不断地旋转,但随着时间延迟,作用于颗粒表面诱导电荷的电应力会产生两个主要影响:传统的同相介电泳力会使极化率更低的杆状颗粒移向场中心(电场最弱的区域)

;由于界面处电导率的跃变,异相的电旋转转矩使极化胶体在界面电荷弛豫频率附近发生异步旋转

。

古代的筝弦数量不定，有过十二弦、十三弦、十六弦等，目前古筝的统一规格是二十一弦。要区分瑟和筝，现在比较简单的方法就是数弦的数量了。一般是，二十五弦为瑟，二十一弦为筝。

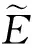
2015年5月，学院为落实“中国制造2025”行动纲领，对接国家“互联网+”行动计划，顺应南京市及周边地区智能制造技术产业需求，进一步提升内涵建设水平，打造核心竞争力，在中国航天科技集团总工程师、国家智能制造重大工程联合论证专家组组长杨海成教授的指导下成立智能制造学院。通过不断的实践锻炼，有力提升了学生的创业素质。

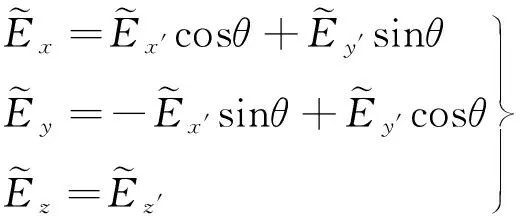
(2)

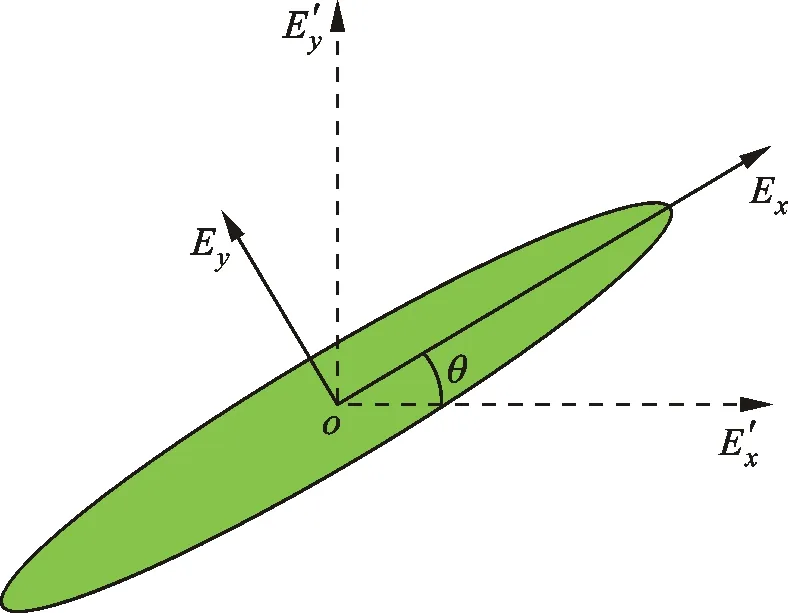
假设杆的长轴与电场的水平分量成一定角度

,沿每个主轴(

=

,

,

)的复偶极矩

如下式

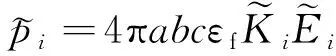
(3)

从点偶极子的理论出发,得到了由于宏观的Maxwell-Wagner结构极化而作用于杆颗粒的场平均旋转力矩

的一般表达式为

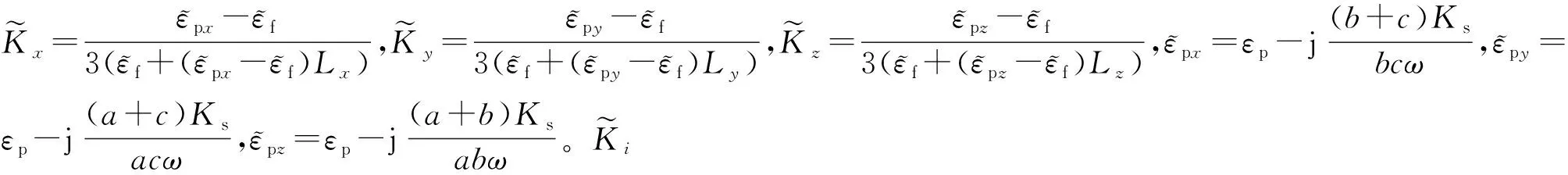
下面介绍一个持续长度的概念,它是蠕虫状链模型中的重要参数.对于一条由键长为l、键角为α的n个键所组成的大分子链,将第一个键的方向看成z轴(见图1),那么第二个键以α角与之相连,键矢量间的夹角为θ,第三个键又以α角与第二个键相连,其键矢量间的夹角亦为θ,依次类推,这条链的末端距在z轴上投影的平均长度即为n个键矢量在z轴投影长度的加和:

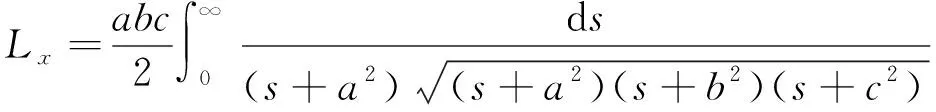
(4)

=

=

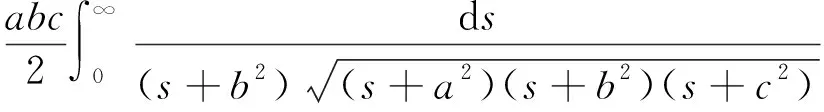
(5)

浅俗的，让你快乐；艰涩的，让你智慧；横看可成岭，侧看则成峰，最最有趣的，倒是那“只缘身在此山中”的忘情体验。

=0

069 1

(6)

=

=0

465 5

(7)

其中

例4宜兴窑紫砂梅花鹿原译：This standing beige boccaro (zisha) deer is craning its neck and holding its head up.With the additions of painted fur and white spots,it is a realistic representation.

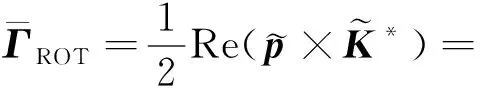
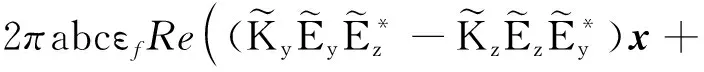
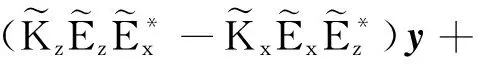
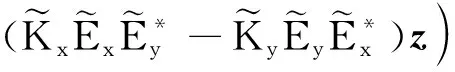
(8)

2

1

2 电旋转转速分析 在没有悬浮电场时外加旋转电场为

(

),该电场以角频率

=2π

顺时针传播,施加在远离目标介电微杆的地方

(

)=

(cos(

)

′-sin(

)

′)

(9)

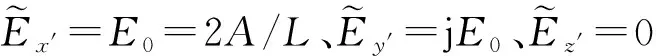
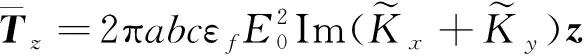
(10)

1993年，美国国会通过的《政府绩效与结果法案》，首次从立法上对美国联邦机构绩效评价做出了制度性规定。该法案将资源和管理决策与绩效挂钩，建立以绩效为目的的预算制度，将美国政府的绩效管理重点由“过程问责”转向“结果问责”，由“投入—产出”模式转为“目标—结果”模式[3]，促使联邦部门和机构在预算中加强“战略—目标—预算—绩效”的闭环管理，提高政府管理绩效和服务效率。

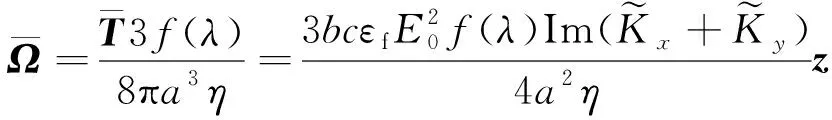
(11)

(

)=

-(1

14+0

2

+16

-63

+62

)

(12)

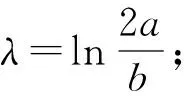
2

2

1 旋转诱导电荷电渗流场颗粒旋转角速度解析解推导 通过将边缘长度为

的方形偶极微电极嵌入电场中心,

=300 μm,实现了驱动模式从反场旋转到同场旋转的过渡,如图2c和图4所示。诱导双电层的特征弛豫频率为

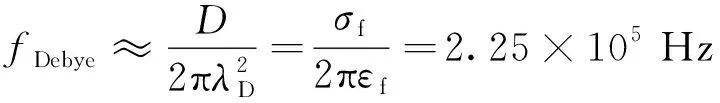
(13)

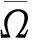
2.2 介电微杆同场旋转行为

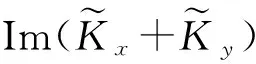
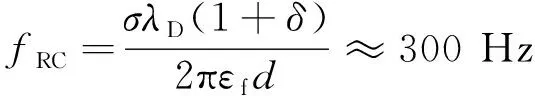
(14)

式中:

为紧实层

和扩散层

之间的电容比,当外加电场频率远超过

时,由于电场的极性变化很快,不允许过多的反离子在德拜层中积累

。悬浮的偶极电极的理想可极化表面发射出较强的垂直电场分量,这意味着水平场分量

和

比垂直场分量

小至少一个数量级。因此,式(8)中的第3项可以忽略。由于

≫

,在金属正方形表面上的电旋转转矩只有

分量,导致杆在进入电极表面时在

平面中滚动运动,平均旋转力矩为

社会公平的本质是公共服务资源空间配置的合理性及带有补偿性质的分布公平性，强调应当向特定的社会弱势群体倾斜.老年人日常前往养老服务设施较多选择步行，而中心城区老年人口集聚的区域在步行方式下的可达性值较低，资源配置空间公平性较差，应在老年人口集聚的中心城区和新建开发区加大公共养老服务资源的投入，使得养老服务设施空间布局更加合理，从而在一定程度上实现社会公平，体现城市以人为本的发展理念.

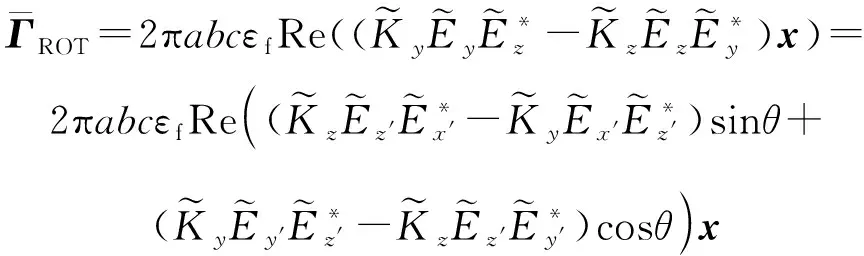
(15)

利用悬浮介质对杆表面施加的黏性液体应力来平衡电旋转转矩,得到了旋转电场中杆状刚体的稳定平均角速度

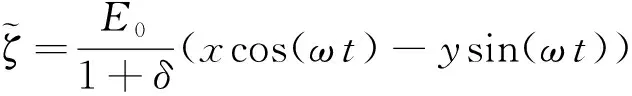
(16)

根据亥姆霍兹公式,旋转电场下悬浮电极上方ICEO滑移的瞬态表达式为

将

=23

5 μm和

=

=5

5 μm代入式(4)(5)求积分得

(

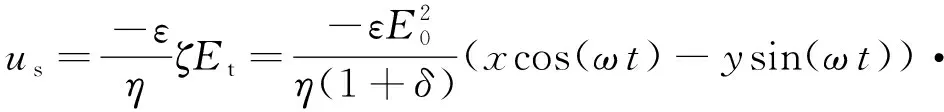
cos(

)-

sin(

))

(17)

其中

=

(

cos(

)-

sin(

))。滑移流场

有一个流动停滞线

=cot(

),在存在悬浮电极的情况下会导致介电杆的旋转。将滑移速度方程式(17)在极坐标(

,

)下的角分量分解为

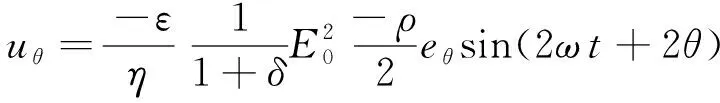
(18)

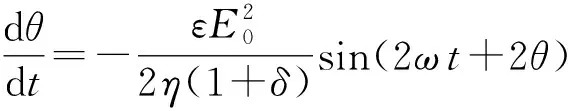
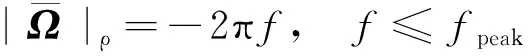
(19)

≥

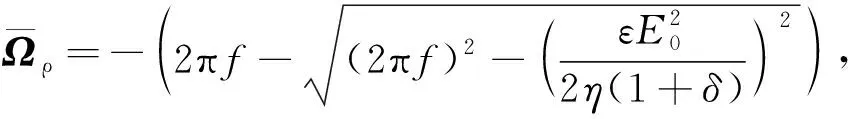
(20)

(21)

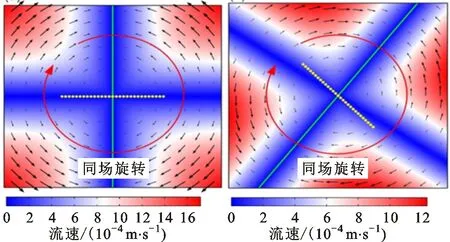
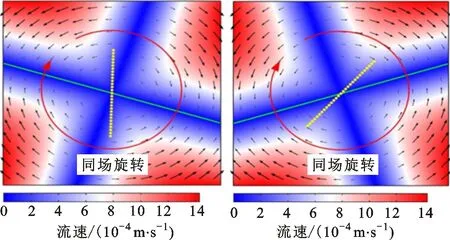
式(19)～(21)中的负号表示粒子是沿电场顺时针方向旋转的,当频率为理想频率时,即

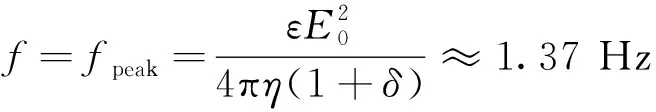
(22)

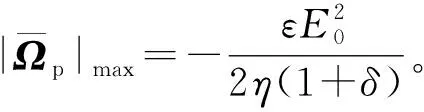
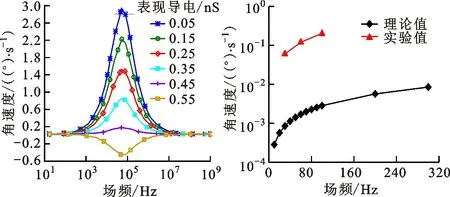
从图5b可知,当频率低于50 Hz时,由于交流电场中的固有表面电荷导致微杆的振荡电泳运动,严重影响粒子的旋转行为,使理论预测高于实验测量。图5b中,当频率大于80 Hz时,在没有其他非平衡电表面现象的情况下,实验的结果与基于Debye-Huckel理论的分析结果近似。当理论频率

≫

时,频率相关性

∝1

与RC特征频率

≈300 Hz以下的测量数据高度吻合。然而,如图5c中,超过

的部分,理论预测的下降趋势比实际测量的更明显,因为当前的数学分析所排除的电化学离子弛豫效应会进一步降低ROT-ICEO的流速。特别的,100 Hz时旋转角速度达到-3.15(°)/s。此外,对固定

=100 Hz的电压依赖性比较表明,转速测量数据遵循

(2<

<3)的指数增长规律,略大于作为驱动源本身的流体的二次电压依赖性增长趋势。理论上ROT-ICEO转速随电压增长成四次方的趋势

∝

是在没有壁面摩擦力的情况下得到的,而壁面摩擦力可能在引起观察到的差异中起重要作用。因此对于ROT-ICEO引起的介电微杆的电压依赖性旋转特性的研究还有待进一步深入。

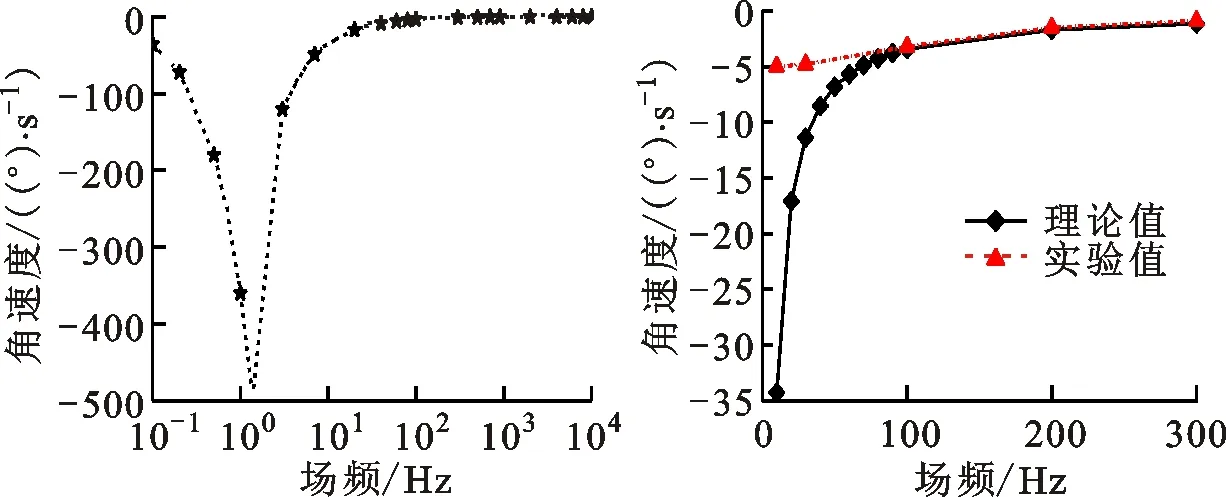
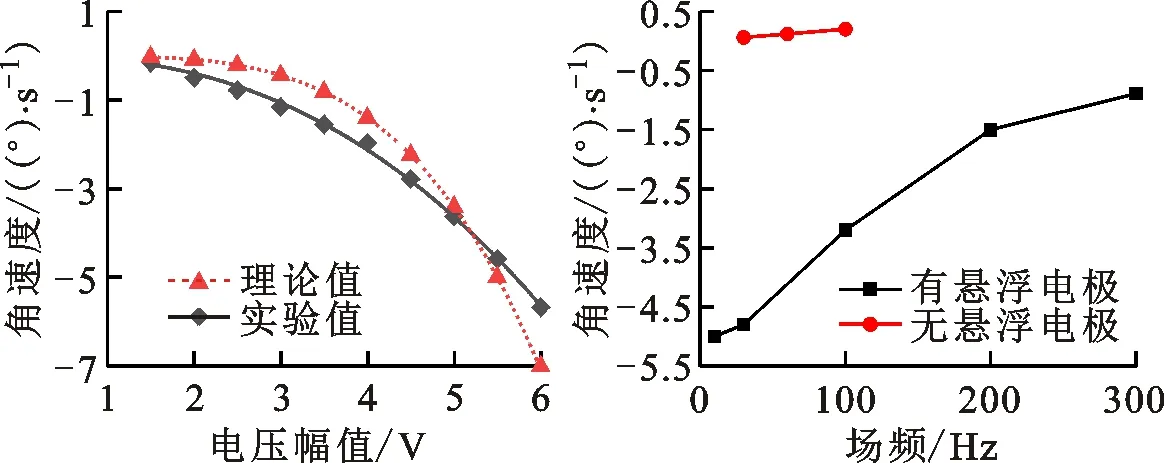
图5中,虽然所得到的旋转速度很慢,但无悬浮电极时的电旋转和有悬浮电极时的ROT-ICEO这两种方法都显示出了较好的应用前景。与通常用于介电特性表征的电旋转不同,在悬浮电极上由于ROT-ICEO而引起的介电粒子旋转方程,对粒子自身性质的依赖性较小,电场强度或其他系统物化属性与粒子参数无关。这种方法几乎不受焦耳热的影响,因此它们的温和性可以很容易地用于处理芯片实验室中的生物样品。为了进一步加快粒子的旋转速度,可以使用高阶相位来表示背景旋转场,使其更像一个理想的正弦波,产生更强的电动效应。

3 结 论

本文证明了在没有布置任何结构化悬浮电极的情况下,当电杆表面电导率

小于0.55 nS时出现介电微杆的反场旋转,而悬浮在电解质溶液中的介电微杆的旋转行为可以通过在旋转电场中布置结构化的悬浮微电极来进行主动调节。曲面上非均匀表面传导增强Maxwell-Wagner界面极化,介电杆在电旋转力矩作用下与施加的旋转电场相反方向旋转,100 Hz时平均角速率为0.18(°)/s。然而,在微器件中嵌入偶极悬浮电极时,ROT-ICEO产生的流体动力转矩在金属表面产生了同场旋转,100 Hz时其平均角速度为-3.15(°)/s。这种方法不仅实现了从反场到同场电动旋转行为的灵活调节,而且大大加快了运动的角速度,这可对电动力学、分析化学和微流体等交叉学科研究领域提供一定的参考。

:

[1] 陈琰, 安立宝. 粒子受介电泳力作用运动的仿真研究 [J]. 固体电子学研究与进展, 2015, 35(1): 25-30.

CHEN Yan, AN Libao. Simulation of particle motion caused by dielectrophoretic force [J]. Research & Progress of Solid State Electronics, 2015, 35(1): 25-30.

[2] HUANG Liang, ZHAO Peng, LIANG Fei, et al. Single-cell 3D electro-rotation [J]. Methods in Cell Biology, 2018, 148: 97-116.

[4] LAPIZCO-ENCINAS B H, RITO-PALOMARES M. Dielectrophoresis for the manipulation of nanobioparticles [J]. Electrophoresis, 2007, 28(24): 4521-4538.

[5] KIM D, SONKER M, ROS A. Dielectrophoresis: from molecular to micrometer-scale analytes [J]. Analytical Chemistry, 2019, 91(1): 277-295.

[6] SHANKAR B M, KUMAR J, SHIVAKUMARA I S. Numerical investigation of electrohydrodynamic instability in a vertical porous layer [J]. Applied Mathematics and Computation, 2017, 310: 15-39.

[7] MAVROGIANNIS N, DESMOND M, LING K, et al. Microfluidic mixing and analog on-chip concentration control using fluidic dielectrophoresis [J]. Micromachines, 2016, 7(11): 214.

[8] ZHOU Teng, YEH L H, LI Fengchen, et al. Deformability-based electrokinetic particle separation [J]. Micromachines, 2016, 7(9): 170.

[9] 姚佳烽, 姜祝鹏, 赵桐, 等. 多电极阵列微流控芯片内细胞介电泳运动分析 [J]. 分析化学, 2019, 47(2): 221-228.

YAO Jiafeng, JIANG Zhupeng, ZHAO Tong, et al. Analysis of cell dielectrophoretic motion with microfluidic device embedding multi-electrodes [J]. Chinese Journal of Analytical Chemistry, 2019, 47(2): 221-228.

[10]LAPIZCO-ENCINAS B H. On the recent developments of insulator-based dielectrophoresis: a review [J]. Electrophoresis, 2019, 40(3): 358-375.

[11]DU Xiaotian, MA Xiao, LI Hang, et al. Validation of Clausius-Mossotti function in wideband single-cell dielectrophoresis [J]. IEEE Journal of Electromagnetics, RF and Microwaves in Medicine and Biology, 2019, 3(2): 127-133.

[12]MORGANTI D, MORGAN H. Characterization of non-spherical polymer particles by combined electrorotation and electroorientation [J]. Colloids and Surfaces: A Physicochemical and Engineering Aspects, 2011, 376(1/2/3): 67-71.

[13]崔祥干, 丁海涛, 杜山. 交流电热流对导电岛纳米电极介电组装的影响 [J]. 西安交通大学学报, 2020, 54(2): 127-136.

CUI Xianggan, DING Haitao, DU Shan. Influence of AC electrothermal flow on dielectro-phoretic assembly in a conductive-island nanogap electrode system [J]. Journal of Xi’an Jiaotong University, 2020, 54(2): 127-136.

[14]LIU Zhijian, LI Di, SONG Yongxin, et al. Surface-conduction enhanced dielectrophoretic-like particle migration in electric-field driven fluid flow through a straight rectangular microchannel [J]. Physics of Fluids, 2017, 29(10): 102001.

[15]闫姿姿, 李姗姗, 李铭浩, 等. 交流电热流场对微纳粒子介电泳行为的影响 [J]. 机械工程学报, 2017, 53(14): 202-208.

YAN Zizi, LI Shanshan, LI Minghao, et al. Influence of AC electrothermal flow on the d ielctrophoretic behaviors of micro-nano particles [J]. Journal of Mechanical Engineering, 2017, 53(14): 202-208.

[16]MANSHADI M K D, MOHAMMADI M, ZAREI M, et al. Induced-charge electrokinetics in microfluidics: a review on recent advancements [J]. Journal of Micromechanics and Microengineering, 2020, 30(11): 113001.

[17]ABDALLAH B G, CHAO T C, KUPITZ C, et al. Dielectrophoretic sorting of membrane protein nanocrystals [J]. ACS Nano, 2013, 7(10): 9129-9137.

[18]VIEFHUES M, EICHHORN R. DNA dielectrophoresis: theory and applications a review [J]. Electrophoresis, 2017, 38(11): 1483-1506.

[20]GENCOGLU A, OLNEY D, LALONDE A, et al. Dynamic microparticle manipulation with an electroosmotic flow gradient in low-frequency alternating current dielectrophoresis [J]. Electrophoresis, 2014, 35(2/3): 362-373.

[21]PAUL A, MUKHERJEE S, DHAR J, et al. The effect of the finite size of ions and Debye layer overspill on the screened Coulomb interactions between charged flat plates [J]. Electrophoresis, 2020, 41(7/8): 607-614.

[22]KHAIR A S, SQUIRES T M. The influence of hydrodynamic slip on the electrophoretic mobility of a spherical colloidal particle [J]. Physics of Fluids, 2009, 21(4): 042001.

[23]BAZANT M Z, KILIC M S, STOREY B D, et al. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions [J]. Advances in Colloid and Interface Science, 2009, 152(1/2): 48-88.

[24]LALONDE A, ROMERO-CREEL M F, SAUCEDO-ESPINOSA M A, et al. Isolation and enrichment of low abundant particles with insulator-based dielectrophoresis [J]. Biomicrofluidics, 2015, 9(6): 064113.