基于全局响应面法的镁合金客车骨架优化设计

黄登峰，张建春，林光磊，闫晓磊，石志纲

(1.福建工程学院，福建 福州 350118；2.福建省汽车电子与电驱动重点实验室，福建 福州 350118；3.福建坤孚股份有限公司，福建 龙岩 364302)

纯电动公交客车轻量化至关重要。研究表明，整车质量每降低10%，能源消耗就会降低6%～8%，对于纯电动车而言，减少质量能极大提高客车的续航里程[1-4]。因此对于客车车身骨架进行轻量化研究具有重要的现实意义。

对于客车轻量化技术的研究已取得了系列成果，主要有优化设计方法、新型材料技术、先进的制造技术及连接工艺[5-6]。在优化设计方法的相关研究中，胡涛[7]进行四种典型的工况静力学分析和模态分析，利用灵敏度分析和多目标优化等方法，对客车车身骨架进行轻量化分析。陈鑫[8]建立了参数化模型，基于拓扑优化结果，得出框架式车身结构，并构建响应面近似模型，用于多目标优化设计，最终实现了减重的效果。Wenjie Zuo[9]提出了双层结构优化模型，首先采用连续近似优化方法，对具有刚度和模态频率约束的车身骨架进行优化，然后使用遗传算法优化部件横截面，最终实现了轻量化效果。Ruiyi Su[10]采用实验与仿真相结合的方法，用于验证仿真分析结果的准确性，构建响应面法和混合径向基函数法建立多个代理模型，对车身结构性能建立相应的约束和目标函数，进行多目标优化处理。

相对于其他金属材料，镁合金有明显的优势，密度只有1.78 g/cm3，将镁合金用于汽车上，相比于铝合金车身质量能减轻15%～20%[11]。张思维[12]将镁合金材料应用到电动汽车上，通过工况分析对局部应力过大区域进行结构改进，同样满足了结构性能的要求。齐建强[13]提出了采用镁合金材料作为客车车身骨架，应用有限元方法从结构优化角度提出客车车身结构轻量化改进方案。综上所述，目前对镁合金客车车身骨架轻量化的研究，缺乏理论支撑和系统性优化设计。

本文采用镁合金材料作为公交客车车身骨架，基于HyperStudy优化平台，建立客车隐式参数化模型，利用部分因子设计法进行灵敏度分析，用于筛选设计变量，采用哈默斯雷采样，构建径向基函数响应面近似模型，应用全局响应面法，建立多目标优化方案，对优化前后的参数化模型结果进行对比分析，选出轻量化效果显著的方案，并对模态、刚度、强度等性能进行验证分析。

1 镁合金公交客车骨架有限元模型的建立

1.1 骨架有限元模型的建立

研究对象为12 m长新能源镁合金公交客车，整车骨架采用全承载式结构，由几百根型材杆件组成。在有限元建模前，需进行几何清理，忽略车身上的非承载件，删除对整车骨架无影响的杆件，去除尺寸小于5 mm的结构。整车骨架模型采用壳单元，网格尺寸选择10 mm，对于螺栓孔采用扩孔的方式，使得网格质量雅可比大于0.6，螺栓连接通过RBE2刚性单元代替，焊点采用rigid3刚性单元。所建立的镁合金客车整车车身骨架有限元模型如图1所示。

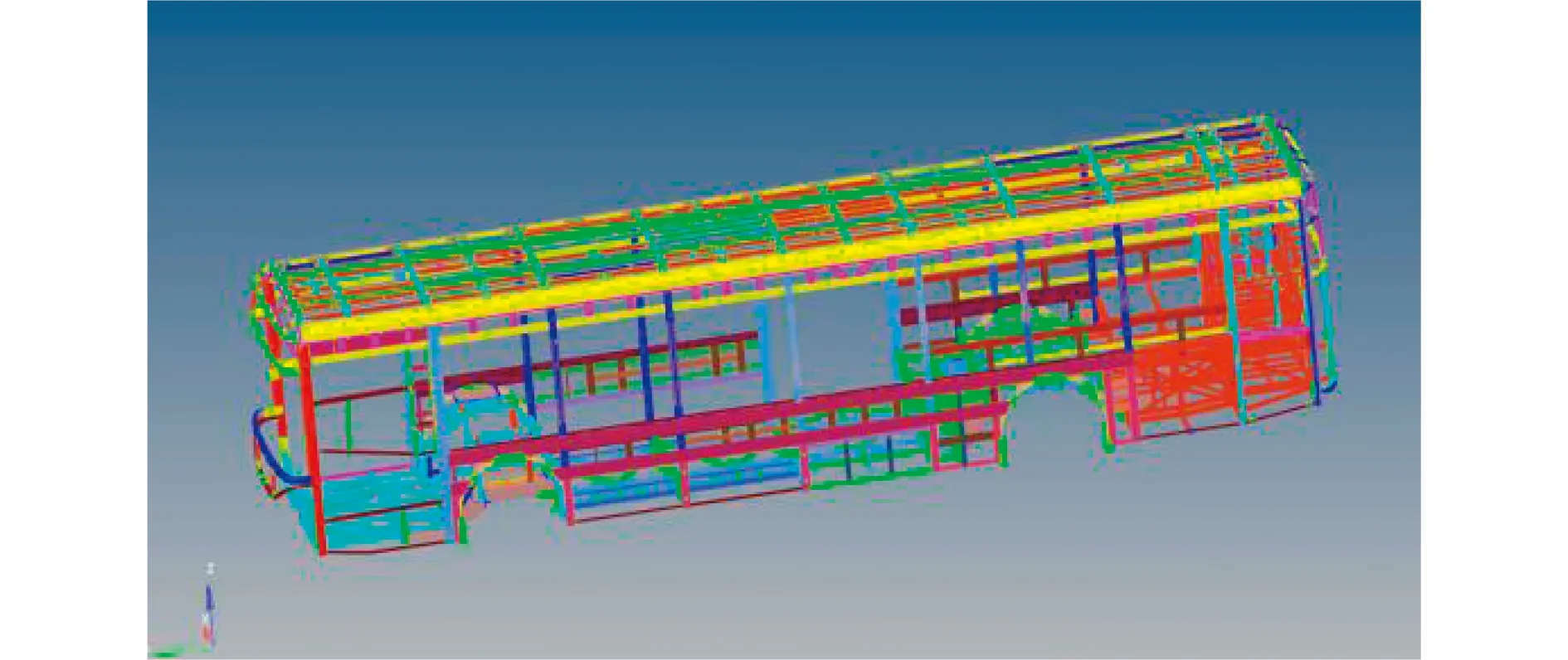
图1 镁合金客车整车骨架有限元模型Fig.1 Finite element model of magnesium alloy bus frame

1.2 材料的选择

客车模型主要运用了镁合金和高强度钢材料。底架承受了客车大部分载荷，需要一定的强度和刚度，因此底架采用Q345矩形方钢结构焊接而成，空气弹簧支架处选用Q500钢。车身五大板块对于支撑车身载荷以及增强车身性能具有重要作用，采用ZK61M镁合金材料。材料属性如表1所示。

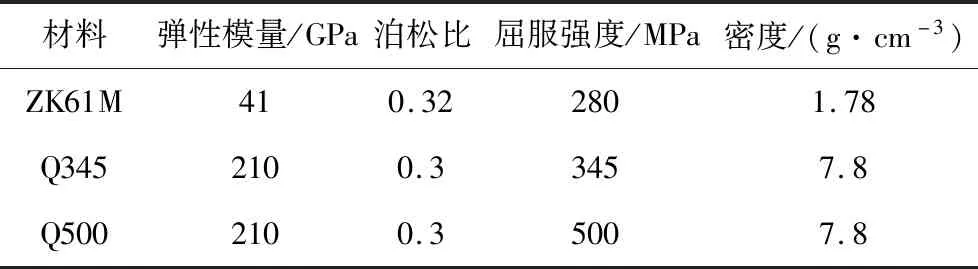
表1 车身骨架材料参数Table 1 Parameters of autobody frame materials

2 基于Hyperstudy的多目标尺寸优化设计

为了减轻镁合金整车骨架重量，降低生产成本，改善整车结构性能，需要对整车骨架进行多目标尺寸优化处理。

多目标优化是指在满足约束条件的情况下，对多个目标函数同时进行优化，得出一种最优方案，使得目标函数同时达到最优。遵从试验设计、近似模型的拟合、多目标尺寸优化等步骤，对客车车身骨架展开多目标优化设计[14]，其中优化流程如图2所示。

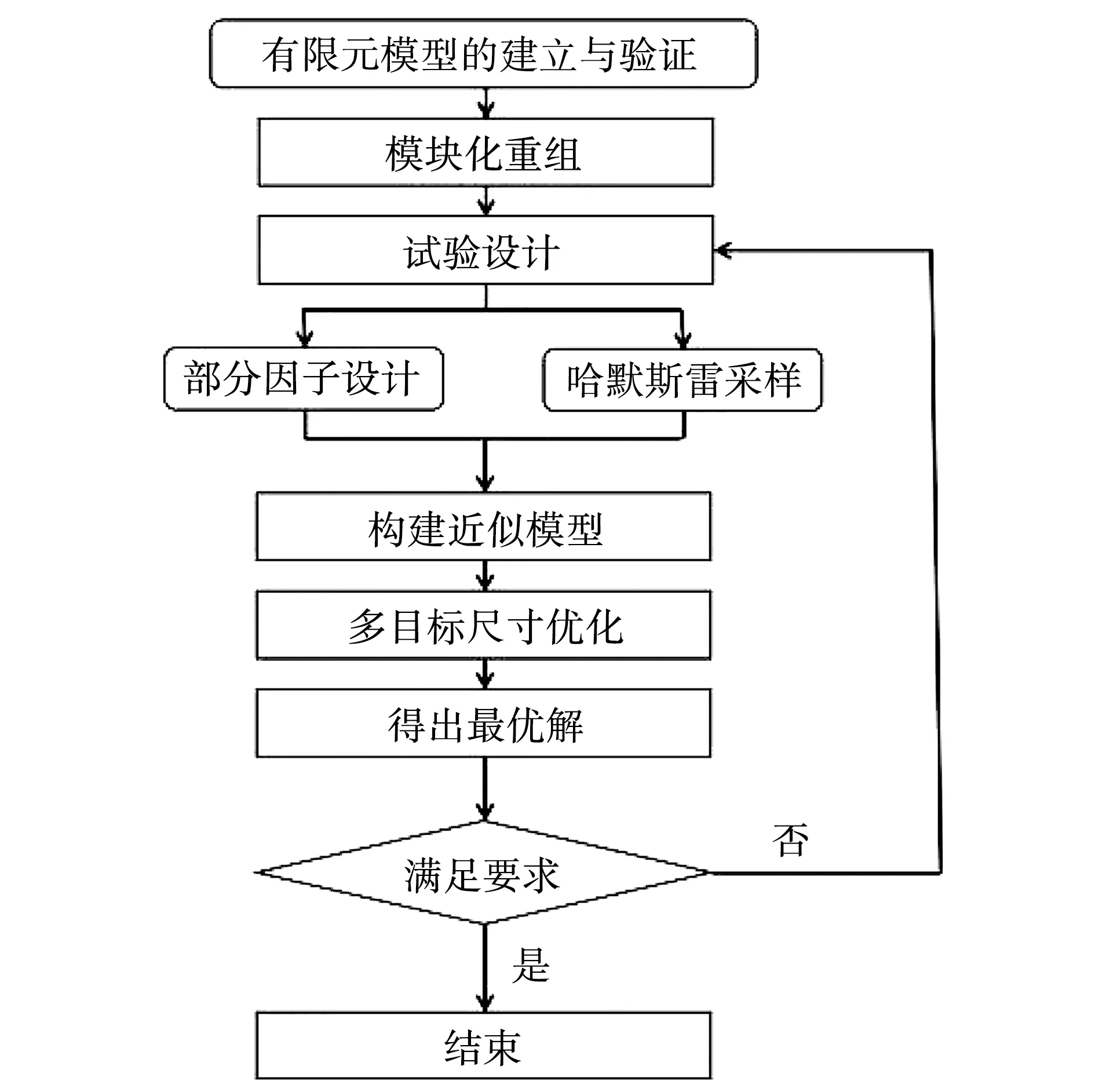
图2 Hyperstudy优化流程图Fig.2 Hyperstudy optimization flow chart

2.1 模块化重组

为了减少设计变量个数，以对称约束为原则，将整车左右对称的骨架杆件厚度合并作为一个设计变量；以应力分布和结构、功能相似性为原则，将作用相同的杆件厚度作为一个设计变量。将几百根杆件整合得出96组设计变量，其中车身五大板块78组、底架18组。为了进一步提高计算效率，通常需要采用试验设计的方法，进行灵敏度分析和响应面的拟合。

2.2 试验设计

DOE试验设计可以用于杆件筛选，筛选出对整车骨架结构性能较为敏感的杆件，对其进行优化分析；也可用于设计空间填充，在整个设计空间内随机均匀采样，其数据可用于后续的响应面拟合。

2.2.1 设计变量的选取

灵敏度分析主要用于计算车身结构性能对车身各杆件的敏感程度，用于筛选优化效果较为明显的杆件，以提高轻量化优化效率。

在HyperStudy中存在全因子设计、部分因子设计等用于灵敏度计算的算法。其中，部分因子设计相较于全因子设计，具有试验次数较少等优点，但同时存在主效应与交互效应混淆等问题，对于存在大量设计变量的情况，部分因子设计仍是最优的选择，其中部分因子设计的示意图如图3所示。

图3 部分因子设计示意图Fig.3 Schematic diagram of partial factor design

对78组表征车身五大板块杆件厚度的设计变量进行 DOE 分析，选用部分因子设计算法，得出128组实验方案，以计算车身结构性能对设计变量的灵敏度[15]。车身结构性能中的数学表达式如下所示。

一阶扭转频率的灵敏度：

(1)

弯曲刚度的第j个设计变量的灵敏度：

(2)

扭转刚度的第j个设计变量的灵敏度：

(3)

式中：

xj—第j组设计变量；即第j组杆件的厚度，j=1，2，…，78；

λi—第i阶模态频率，此处为一阶扭转频率；

φi—相应的第i个特征向量，一阶扭转频率对应的特征向量；

M、K—分别为整体质量矩阵和刚度矩阵；

Kb—弯曲刚度；

Kt—扭转刚度；

Fb—弯曲刚度分析时施加的载荷；

Ft—扭转刚度分析时施加的载荷；

ub、ut—分别为弯曲刚度分析和扭转刚度分析时发生的垂直于地面竖直方向的位移；

L—客车轴距。

经过计算得出的车身骨架质量及结构性能对设计变量的灵敏度数值如图4所示。

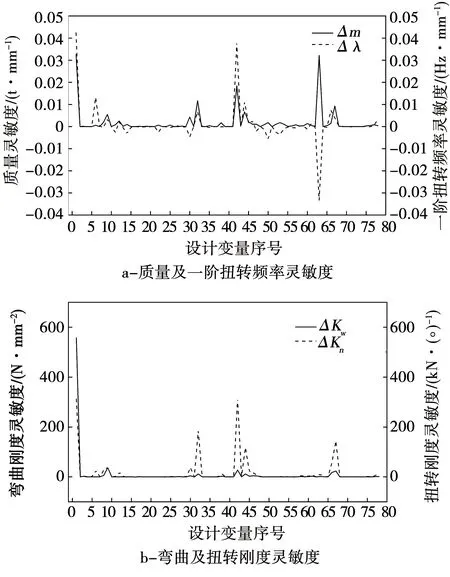
图4 各设计变量灵敏度结果Fig.4 Sensitivity results of each design variable

图中：

Δm—客车整车骨架质量灵敏度；

Δλ—一阶扭转频率灵敏度；

ΔKb—弯曲刚度灵敏度；

ΔKt—扭转刚度灵敏度。

相对灵敏度是车身骨架结构性能对设计变量的灵敏度与质量对设计变量的灵敏度之比[16]，车身骨架的相对灵敏度数值如图5所示。

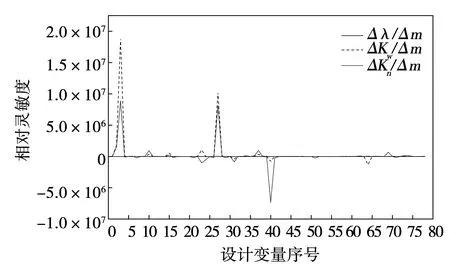
图5 各设计变量相对灵敏度结果Fig.5 Results of relative sensitivity of each design variable

图中：

Δλ/Δm—一阶扭转频率灵敏度与质量灵敏度的比值，Hz/t；

ΔKb/Δm—弯曲刚度灵敏度与质量灵敏度的比值，N/(mm·t)；

ΔKt/Δm—扭转刚度灵敏度与质量灵敏度的比值，m·N/((°)·t)。

通过对比车身结构性能对质量的相对灵敏度数值，筛选出相对灵敏度值较小的25组设计变量，用于后续响应面的拟合。

2.2.2 响应面的拟合

由于底架选用高强度钢材料，且骨架结构性能有裕度，因此具有充足的轻量化空间。选择底架18组杆件及上述筛选的25组杆件厚度作为设计变量进行优化设计，对此n=43组设计变量进行重新编号，筛选的车身杆件厚度设计变量为x1～x25。考虑到计算周期问题，采用空间填充的试验设计算法，用于响应面的拟合。

哈默斯雷采样是一种以面代体的取样方法，能在超立方体中，随机均匀的抽样，且可以用较少的样本，对输出的结果进行评估。为了增加响应面拟合的准确性，采用哈默斯雷采样，抽取200组实验方案，用于作为构建响应面近似模型的数据源。

2.3 构建近似模型

复杂模型的有限元计算周期长，计算量较大。在实际工程应用中，通过响应面近似模型可以预测优化结果，提高实际工程中的优化效率。

径向基函数是对若干基函数进行线性叠加，然后进行拟合，且拟合的响应面都会通过原始数据点，适用于高度非线性的响应。其函数空间表达式：

(4)

用矩阵表示：

Aη=f

(5)

Aij=φ(‖xi-Xj‖)

(6)

式中：

Fφ—径向基函数的函数空间表达式；

n—对应选择优化的设计变量组数，本模拟n=43；

ηj—第j个基函数的权重；

x—输入的变量，即杆件厚度；

φ(‖x‖)—径向基函数；

Xj—函数空间上的第j个样本点，哈默斯雷采样取得的第j个样本点(即第j个设计变量值)；

A—径向基函数表达的函数空间中子空间的一组基；

η—基函数的权重组成的向量；

f—样本点Xj对应的函数值组成的向量。

径向基函数用于存在大量设计变量的情况，具有较高的拟合效率和精确度。选用径向基函数算法，构建近似模型，用于计算后续多目标优化。评价近似模型拟合精度的指标有确定系数(R-Square)和相对平均误差Average。

确定系数(R-Square)用于评价响应面的拟合精度，其值越接近于1，其拟合的精度越高。其数学表达式为

R2=1-SSE/SST

(7)

(8)

(9)

式中：

SSE—和方差，表示原始数据和拟合数据对应点的误差的平方和；

SST—原始数据和均值之差的平方和；

n—对应选择优化的设计变量组数；

zj—第j个原始数据；

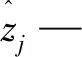
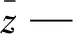
Average是相对平均误差，其值越接近于0，其拟合的误差越小。

采用确定系数(R-Square)、Average两种评估响应面精度的指标，评估响应面拟合的精度，结果如表2所示。根据表2可知，各响应面的R-Square值均在0.9以上，Average值均小于0.2，所以此算法建立的近似模型具有良好的精度。

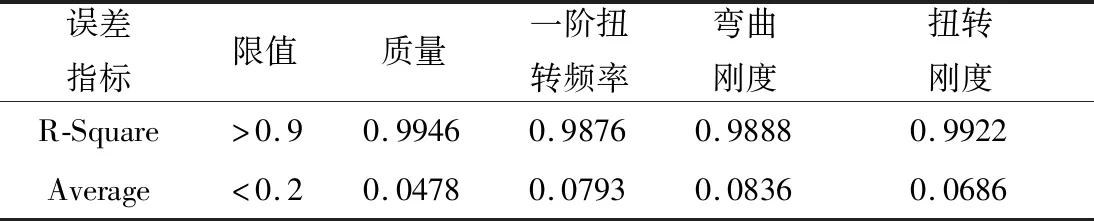
表2 响应面模型精度Table 2 Response surface model accuracy

2.4 基于全局响应面法的多目标尺寸优化设计

响应面法(RSM)运用了数学方法和统计技术，对感兴趣的响应进行提炼，并与相关的控制变量建立简单的函数关系式，用于拟合复杂的模型，其本质是通过筛选试验确定后续优化过程[17]。函数关系式如下所示。

RSM一阶方程：

(10)

式中：

y1—设计目标；

α0,α1,…,αn—待定系数；

xi—第i个设计变量，即第i组杆件的厚度；

ε1—系统的误差。

二阶方程：

(11)

式中：

y2—设计目标；

a0、a1、b1、cij—待定系数；

n—选择优化的设计变量组数；

ε2—系统的误差。

全局响应面法(GRSM)是一种基于响应面的直接优化方法，且在优化过程中能够不断进化。这种算法可基于较少的数据点，构建一个迭代步的响应面，在每一轮迭代之后，都会产生新的采样点，然后构建一个新的DOE，在新的DOE中求解优化问题，其最优解被用于下一轮迭代，直到达到设定的最大评估数时优化停止。GRSM优化流程如图 6所示。

图6 GRSM优化流程图Fig.6 GRSM optimization flow chart

全局响应面法相较于自适应响应面法，不仅适用于多目标优化，具备全局搜索能力，而且适用于存在大量设计变量的情况，计算效率更高。选用全局响应面算法对整车骨架进行多目标尺寸优化设计，以质量最小、一阶扭转频率最大作为目标函数，弯曲刚度大于9 000 N/mm，扭转刚度大于14 000 N·m/(°)为约束，进行多目标优化设计。其数学表达式为

(12)

式中：

f(x)—目标函数；

f1(x)—质量目标函数；

f2(x)—一阶扭转频率目标函数；

x—由经过灵敏度分析筛选出的设计变量和底架设计变量组成的向量；

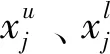
j—对应选择优化的设计变量序号。

优化结果表明，在迭代3 125次后得出多目标优化解集，即Pareto前沿，如图7所示。权衡各优化方案，选出对整车质量优化最显著的方案，即质量为2.17 t，一阶扭转频率为6.03 Hz。

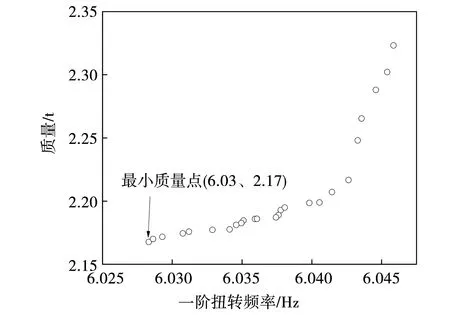
图7 Pareto前沿Fig.7 Pareto frontier

此优化过程中，设计变量采用连续型，考虑到挤压工艺及制造成本等[18]，对优化设计变量进行圆整处理，车身部分设计变量优化上下限及优化结果如表3所示。

表3 车身部分设计变量优化区间及结果Table 3 Optimization interval and results of auto body design variables

2.5 优化前后车身结构性能的对比分析

根据HyperStudy优化后的参数化模型结果，对有限元模型材料属性厚度进行更新，对优化前后的结构性能进行分析，在OptiStruct求解器中求解计算。

优化结果表明，优化后客车一阶扭转频率为5.65 Hz，相较于优化前有所增加，实现了一阶扭转频率大于5.5 Hz，能够有效避免激振频率。优化前后模态频率及振型描述如表4所示，主要模态振型对比如图8所示。

图8 优化前后车身骨架模态振型对比Fig.8 Comparison of modal shapes of body frame before and after optimization

由表4及图8可知，优化前后模态固有频率及振型结果无明显差别，满足车身骨架设计要求。

表4 优化后模态频率及振型Table 4 Optimized modal frequency and modal shape

优化后弯曲刚度、扭转刚度均有所降低，但都满足对整车骨架结构性能的要求，且整车骨架质量相较于优化前减轻了799 kg，减重22.8%，其中优化后车身骨架镁合金部分重量为704.1 kg，减轻了61.1 kg，减重8.0%。

上述优化结果表明，基于近似模型作为数据源，采取全局响应面优化算法经过3125次迭代计算，取得了较为理想的轻量化效果。其中优化前后车身骨架各结构性能如表5所示。

表5 优化前后车身骨架结构性能表Table 5 Performance table of body frame structure before and after optimization

3 优化前后车身骨架强度对比分析

对客车进行水平弯曲工况、极限扭转工况、紧急制动工况和紧急转弯工况的强度分析，优化前后各载荷和工况保持不变，得出优化前后应力分布图如图9所示，最大应力值如表6所示。

图9 优化前后四种工况应力对比云图Fig.9 Stress comparison nephogram of four working conditions before and after optimization

表6 各工况优化前后最大应力值Table 6 Maximum stress value before and after optimization of each working condition

由表6和图9可知，优化后四种工况整体应力水平均有大幅度增加，其中极限扭转工况应力值增加幅度最大，且优化后四种工况最大应力值均小于屈服强度，满足整车骨架强度要求，验证了轻量化优化方案的可行性。

4 结 论

1)基于镁合金公交客车参数化有限元模型，应用部分因子法，进行骨架杆件厚度的相对灵敏度分析，运用哈默斯雷采样，构建了整车结构动静态性能的径向基函数近似模型。

2)以质量最小、一阶扭转频率最大为目标，以弯扭刚度为约束，采用全局响应面多目标优化法对镁合金客车车身骨架进行了尺寸优化，实现了客车骨架结构的轻量化设计。优化前后结果对比表明：在满足其车身结构性能的前提下，整车骨架减重达799 kg，减重率达22.8%。

3)采用轻量化效果更显著的ZK61M镁合金作为客车车身骨架材料，结合多目标结构优化设计方法，不仅满足了车身骨架模态、刚度、强度等结构性能要求，而且减重效果明显，具有较好的工程应用价值。