面向农业旅游的人工智能路线规划算法应用研究

王 润

（无锡城市职业技术学院旅游学院，江苏 无锡 214000）

旅游是大多数人在工作之余会选择的放松方式之一；旅游业为各个地区的经济发展提供了重要支撑［1］。近年来，各县、村积极响应国家乡村振兴战略要求，农业旅游是被重点关注的方面［2］。人们在旅游时通常会选择陌生城市，因此需要根据该区域对于景点的介绍自行制定旅游方案，也可在当地跟团旅行。但这两种方式普遍存在耗时长、路线规划不合理的现象，无法给予人们较好的旅游体验。因此，人们开始关注路线规划算法方面的研究，目前在旅游路径规划研究中应用较为广泛的是蚁群算法和遗传算法。

李磊等［3］提出了一种蚁群优化算法，并将其应用于旅游线路规划。试验结果表明，经过优化的蚁群算法能够有效提高路径的搜索速度，且缓解了景点的拥堵情况。陈雄等［4］提出一种改进的最大最小蚁群算法来进行旅游线路规划。试验结果表明，该算法与其他算法相比较拥有更好的性能，可有效规划出较好的旅游线路。Damos 等［5］将遗传算法和层次分析法应用于多个冲突目标下的城市旅游线路规划评价，结果表明该方法比其他选择路径的方法更准确、更直观。

传统的遗传算法无法利用系统的反馈信息，求解到一定程度时会造成过多的无用迭代，无法得到较好的解［6］；而蚁群算法在路径搜索初期会由于信息素不存在或过少导致算法收敛速度慢和易陷入局部解［7］。基于此，本研究首先对蚁群算法和遗传算法的基础理论进行详细阐述；其次，将两种算法进行融合，提出了一种蚁群-遗传（Ant colony-genetic algorithm，AC-GA）融合算法。两种算法互补可有效弥补各自的缺陷，在旅游路线寻优中发挥其最大优势，对于提高乡村农业旅游线路规划的效率和质量、促进区域经济发展具有重要意义。

1 材料与方法

1.1 试验材料

本试验以乡村农业旅游特色较为突出的江苏省某县为例，开展相关旅游线路规划算法研究。该县共有15 个较为热门的景点，通过导航软件定位得到每个景点的经纬度坐标。

设景点r的经纬度坐标为(xr,yr)，景点s的经纬度坐标为(xs,ys)，则2 个景点之间的实际距离可由如下公式进行计算。

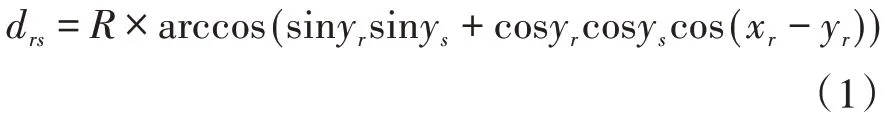
式中，R=6 371 km，代表地球半径。

1.2 试验方法

1.2.1 遗传算法概述 遗传算法是模仿生物进化过程中的优胜劣汰遗传机制而产生的随机进化搜索方法，是通过搜索最优解来解决问题的启发式算法［8］。其基本思想是将生物界的繁殖、杂交、变异以及竞争的概念引入算法；在初始种群生成后，对其中的个体进行优胜劣汰的选择，通过交叉以及变异产生下一代种群等操作，以此从有限个问题解中找出最优的一个［9］。生物遗传术语在遗传算法中的对应关系如图1 所示。

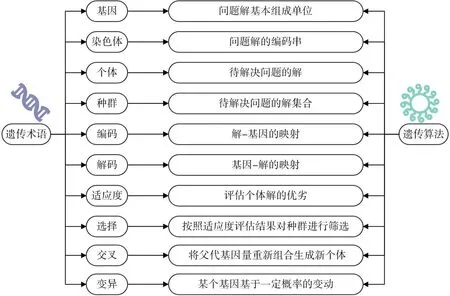
图1 遗传术语在算法中的对应关系

解决一个特定问题可以有很多种方法，而初始种群就是由这些问题解随机排列组成的，种群中的所有个体被视为染色体，个体的优劣采用适应度函数评判，适应度值越大则代表个体越优秀。按照适应度值的大小对父代进行筛选，淘汰较差的个体，将优秀个体经过交叉和变异来产生下一代种群，通过不断循环迭代，解的质量越来越好，最终算法收敛于最合适的解，当前种群所对应的问题结果即为最优解［10］。遗传算法的基本流程如图2 所示。

图2 遗传算法的基本流程

常用的遗传操作算子有选择算子、交叉算子以及变异算子3 种，其中，选择算子是遗传算法，具备以下几个优点：算法可将问题的参数编码成基因片段并进行循环迭代优化，由于直接作用于参数本身，因此不受函数约束条件的限制；算法寻优过程从任意一个种群开始，并非由某一个个体开始，过程中伴随隐含并行搜索，能够在一定程度上降低算法陷入局部最优解的概率。综上所述，遗传算法适用于处理与旅游路线规划类似的非线性组合优化问题。

1.2.2 蚁群算法概述 蚂蚁群在寻找食物时有其特定的配合方式，而蚁群算法是模拟这一过程而产生的一种算法［11］。蚂蚁会在其经过的路径上释放信息素，以此来进行标记和向同伴传递信息；蚁群会自发地选择信息素浓度更高的路径移动［12］。随着时间的推移，当某一条路上的蚂蚁数量越多，其路径上的信息素浓度就越高，进而选择此路径的蚂蚁就会越来越多，因而逐渐表现出一种正反馈现象，这就能够很快找到最优路径［13］。其原理如图3 所示。

图3 蚁群算法原理

蚂蚁主要是根据路径上的信息素浓度与启发式函数对下一步的节点进行选择的［14］。设一个蚁群共有m只蚂蚁，假定其中的第k只蚂蚁目前在节点r处，则可按照如下公式对下一节点s进行选取。

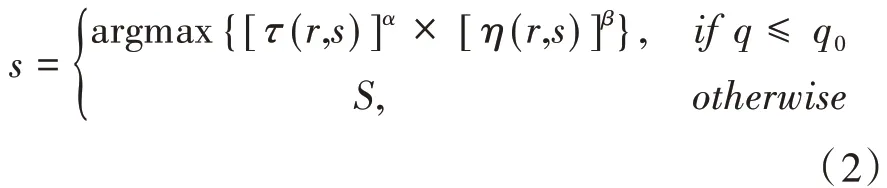
式中，τ(r,s)为节点r与s之间的信息素强度；α为启发因子；β为期望启发因子；η(r,s)为能见度的启发式信息，即启发函数；其为r与s之间距离的倒数，即：

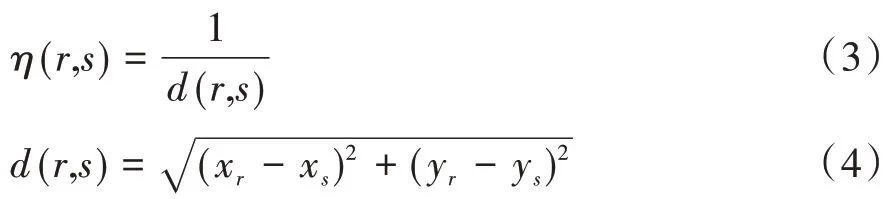
q为[0,1]区间上的随机数，q0为[0,1]区间上的给定数。若q＞q0，根据如下公式对可行节点s进行选择。

式中，Pk(r,s)为蚂蚁k从r转移到s的概率。蚂蚁k经过的全部节点均被记录在禁忌表Tabuk之中，则有：

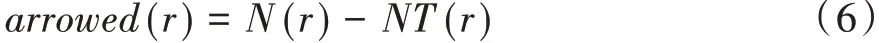
式中，arrowed(r)为蚂蚁k在节点r处的可行节点集合；N(r)为蚂蚁k在节点r处周围所有可行节点的集合；NT(r)为节点r周围禁忌节点的集合。

各个路径上的信息素浓度不会一直保持不变，而是会随时间逐步挥发。将信息素挥发因子表示为ρ，用1-ρ表示残留的信息素浓度，每只蚂蚁通过1个节点后可用如下公式进行局部信息素的更新。

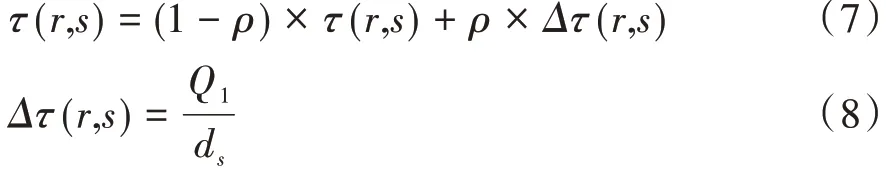
式中，Q1为常数；ds为蚂蚁k已经走过的路径总长。每只蚂蚁在完成1 次循环后，需要对全局信息进行更新。通过以下公式对全局信息素进行更新。

式中，Q2为常数；Lkmin为本次搜索中的最短路径长度；(r,s) ∈GlobalBestTour为蚂蚁k所经过的路径(r,s)的最短路径；Δτkr,s为蚂 蚁k在 搜索后留在r与s之间路径上的信息素增量。

蚁群算法的实现流程见图4。

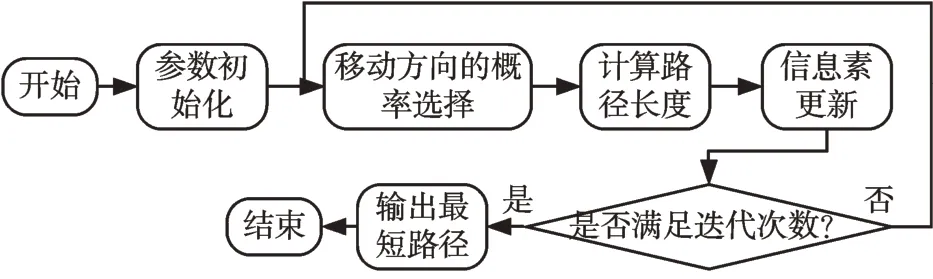
图4 蚁群算法的实现流程

1.2.3 蚁群-遗传融合算法 传统的遗传算法无法利用系统的反馈信息，求解到一定程度时会造成过多的无用迭代，无法得到较好的解。传统的蚁群算法在路径搜索初期会由于信息素不存在或过少而出现寻优无头绪的情况，使得算法极易出现收敛速度缓慢以及陷入局部最优解的问题。为解决上述问题，提出了AC-GA 融合算法。融合算法路径寻优步骤如图5 所示。

图5 融合算法流程

第1 步，将目标问题中的景点采用1～N的实数进行编码，并随即排列。

第2 步，编码后对种群以及算法的参数进行初始化。

第3 步，将2 个景点之间的路径长度作为本试验的适应度函数。

第4 步，根据种群中个体的适应度值进行筛选。

第5 步，根据交叉概率将要交叉的种群在对应的片段处进行交叉。

第6 步，根据变异概率选取个体，将其2 个不同位置的片段进行交换，完成变异。

第7 步，不断循环以上步骤，直至满足设定的最大迭代次数，输出目标问题的若干初始解。

第8 步，蚁群算法参数初始化；将由遗传算法输出的初始解转换为信息素，并按照其分布将蚂蚁置于N个节点上。

第9 步，蚂蚁根据计算所得概率移动至下一节点。

第10 步，蚂蚁对所有节点进行一次完整的循环后，增加较短路径上的信息素浓度，并清空途径路径记录表。

第11 步，若已满足前期设置的循环次数，则终止操作，输出最优解；若否，则返回步骤9。

1.2.4 仿真试验方法

1）蚁群算法参数寻优。合适的参数设置对于提高算法的性能有关键作用，起决定性的参数主要有启发因子α、期望启发因子β以及信息素挥发因子ρ。本试验选取Tsplib 国际数据集中的Ei151 子数据集进行算法参数寻优试验。Tsplib 国际数据集是一个包含从十几个节点的小规模问题集至数百个节点的大规模问题集的测试集合［15］；其中，Ei151 数据集的城市规模为50，最短路径长度为426。试验的其他参数设置如表1 所示。

表1 融合算法其他参数设置

每组试验取10 次结果的平均值，并将融合算法的试验结果与单一的蚁群算法进行比较。如，在α寻优过程中，暂设置信息素强度Q= 100，β= 4，ρ=0.5，α在合理范围内取值进行仿真；同理，在确定了α的最佳取值范围后，将其应用于β的寻优过程，Q、ρ取值不变，确定β的最佳取值范围；以此类推，最后对ρ的取值范围进行确定。在对上述结果进行综合考虑后，最后确定α、β和ρ的最佳组合。

2）旅游路径寻优方案。试验以江苏省某县的15个景点作为算法寻优过程中的15个节点，将该县域视作1个坐标轴，各个节点在其中的位置如图6所示。

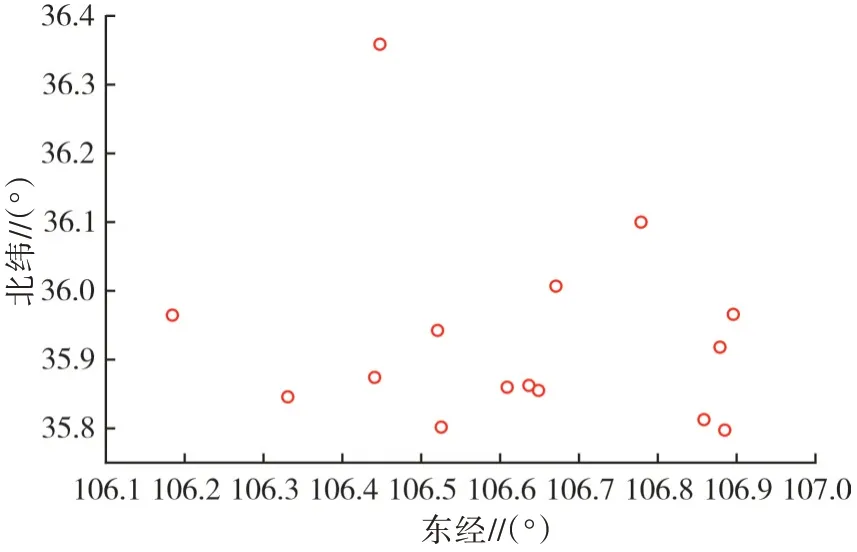
图6 15 个节点的位置示意图

本试验主要采用Matlab 软件对算法的路径寻优过程进行仿真模拟；将路径长度作为算法的适用度函数，并使用AC-GA 融合算法进行路径寻优。

2 结果与分析

2.1 算法参数寻优结果

1）启发因子α。本研究提出的AC-GA 融合算法与传统蚁群算法的α寻优结果如图7所示。由图7可以看出，当α较小时，传统算法在搜索初期具有盲目性，迷失蚂蚁数量以及算法的迭代次数较多；而采用融合算法后迷失蚂蚁的数量有明显减少，相较于传统算法更易搜寻到最优路径。考虑到算法是在α= 1时寻到了最优路径，并且迭代次数以及迷失蚂蚁数量也趋于稳定，因此将算法的启发因子α设置为1。

图7 启发因子α 参数寻优结果

2）期望启发因子β。本研究提出的AC-GA 融合算法与传统蚁群算法的β寻优结果如图8 所示。由图8 可知，采用融合算法在β较小时，明显地减少了迷失蚂蚁的数量以及算法迭代次数，使算法的收敛速度得以提升。在β较大时，传统的蚁群算法易陷入局部最优，但融合算法降低了模型陷入局部最优的几率。算法在β= 7 时，迷失蚂蚁数量以及迭代次数最少并且趋于稳定，因此将β设置为7。

图8 期望启发因子β 参数寻优结果

3）信息素挥发因子ρ。本研究提出的AC-GA 融合算法与传统蚁群算法的ρ寻优结果如图9 所示。由图9 可以看出，传统算法在ρ∈[0.1,0.5]区间内时，虽能够寻得最优路径，但其收敛速度较慢；而融合算法在ρ∈[0.1,0.7]区间内迷失蚂蚁数量远远低于传统算法，并且收敛速度快，曲线稳定，ρ的选取空间更大，表现出更好的性能。当ρ较大时，算法极易陷入局部最优。综合考虑，将算法的信息素挥发因子ρ设置为0.7。综上所述，融合算法的最优参数组合为α= 1、β= 7、ρ= 0.7。

图9 信息素挥发因子ρ参数寻优结果

2.2 算法仿真结果

AC-GA融合算法与传统蚁群算法的仿真结果如图10 所示。由图10 可以看出，采用AC-GA 融合算法与传统蚁群算法输出的路线图有区别。由传统蚁群算法输出的最优路线长度为4 705.486 9 km，ACGA融合算法输出的最优路线长度为2 247.731 6 km，比传统算法短2 457.755 3 km。传统算法在10 次试验过程中的迭代次数平均为164，搜索时间平均为44.40 s；融合算法的迭代次数平均为51，比传统算法少68.9%；搜索时间平均为9.01 s，比传统算法少79.7%。综上所述，AC-GA 算法表现出更优秀的性能，适用于农业旅游路线规划研究。

图10 算法仿真结果

3 结论与讨论

智能算法已在旅游线路规划研究中被广泛使用，其中应用最多的是遗传算法和蚁群算法。但传统的遗传算法和蚁群算法都存在一定的缺陷。基于此问题，首先对蚁群算法和遗传算法的基础理论进行了详细的阐述；其次，提出了AC-GA 融合算法；最后，以江苏省某县的15个景点为例，对算法的性能进行了验证。结果表明，在同一参数设置条件下，采用本研究提出的AC-GA融合算法寻到最优路径时的迭代次数远低于传统的蚁群算法，收敛速度更快。ACGA融合算法输出的最优路线长度为2 247.731 6 km，比传统蚁群算法短2 457.755 3 km。融合算法在10次试验过程中的迭代次数平均为51，比传统算法少68.9%；搜索时间平均为9.01 s，比传统算法少79.7%。综上所述，AC-GA 融合算法的性能优于传统算法，适用于农业旅游路线规划研究。由于文章的篇幅问题，只考虑了路线长度问题，未来还需将景点的热度、开放时间以及费用等问题考虑进算法中，以提供更优的路线规划方案。本研究的开展对于提高乡村农业旅游线路规划的效率和质量，提升游客满意度，进而带动区域发展有重要意义。