产品空间理论测度述评
王文博
一、产品空间理论介绍
在经济学理论发展中,经济增长的相关理论一直处于核心地位。为了更加深入理解经济增长的本质,理解生产能力与制造能力的差异,Hidalgo 等(2007)开创了产品空间理论,尝试使用复杂科学的思路,结合网络科学工具来理解经济增长的实质,以及国家经济背后的生产能力与制造能力[1]。产品空间理论的开创性思想在于利用网络科学将产业网络全貌完整刻画出来,并且打破传统理论中产业同质化的假设,用网络结构完整表征产业的异质性特征。由于产业网络的异质性存在,企业或经济体进行产业升级不仅仅取决于自身的技术实力,也取决于目前产业所处的位置,以及产业之间的距离。
经济复杂性是产品空间理论的核心概念之一,被认为是经济增长的动力源泉。复杂性在经济体中意味着多样化的技能、多样化的专业分工以及足够多的知识资本储备。经济体中只有具有足够的复杂性存在,才能组合碰撞出更高端的知识技能与制造能力,这与熊彼特“创造性破坏”的创新观念不谋而合。与传统经济增长理论相比,经济复杂性思想不去预先定义影响经济增长的因素,而是通过出口贸易数据等客观经济现象表征经济复杂性,进而表达经济体出口行为背后蕴藏的能力。下文将对四种主流经济复杂性测度算法进行评析。
二、经济复杂性的测度方法
(一)出口复杂度EXPY
在产品空间理论提出的最初阶段,Hausmann 等(2007)提出了产品复杂度PRODY 和出口复杂度EXPY用以表征产品生产所需技术的高端程度以及一国的技术与生产能力的高端程度[2]。产品复杂度这一指标基于RCA 指数和显性比较优势的思想构建,它的基本思路是发达国家更倾向于生产技术含量更高的产品,因为更高端的产品通常能够带来更高的收益。基于以上思想的产品复杂度PRODY 构造如下:

其中expc,i,t指在t时期c国出口i商品的贸易量,GDPpercapitalc,t指c国的人均GDP。上式中分子表示某一国家的某一产品出口贸易额在国家的总出口贸易额中的份额,而分母表示所有国家出口此商品的份额汇总。以上比例使用人均GDP 加权则可以将国家的发达程度给产品出口赋予不同的权重,将所有国家赋予权重后的指标累加即可得到表示产品复杂度的指标PRODY。之后将一国所有产品的复杂度与出口份额的乘积累加,即可得到一国的出口复杂度指标EXPY,构造如下:
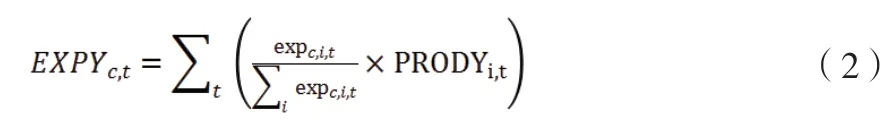
以上出口复杂度EXPY 和产品复杂度PRODY 指标在构建过程中使用了产品出口贸易量的份额来构建指标,同时引入人均GDP 指标对不同国家的出口商品赋予不同的权重,以此来表现复杂度指标背后蕴含的国际贸易理论中相对比较优势和分工理论的思想,但后续研究中学者逐渐认识到出口复杂度EXPY 的指标体系存在较大的理论缺陷。首先最主要的理论缺陷就在于“富国生产富产品”这一假设前提。观察现实世界我们可以发现,在现实经济环境中,落后国家确实常常生产技术简单,附加值低,劳动密集型的产品,但发达国家却不一定只专注于生产高科技产品,而是在控制高科技产业的同时,拥有一个广阔而分散的出口产品分布,这与出口复杂度的假设不符。此时需要更加科学的指标表征复杂性。
(二)经济复杂性指数ECI 与产品复杂性指数PCI
针对出口复杂度EXPY 的不足,Hidalgo 和Hausmann(2009)以RCA 为基础,结合产品空间理论提出了反射法测度经济复杂性指数ECI 和产品复杂性指数PCI 的方法,用以更好的表示经济体的生产与高端制造能力,是目前经济复杂性应用最广泛的测度指标之一[3]。
首先介绍经济复杂性指数测度中的相关概念。显性比较优势RCA(Revealed comparative advantage),用Rcp 表示,指就是区域c 的经济活动p 的观测量(Xcp)与期望值(XcXp/X)之间的比值。对于Rcp >1 的情况,表明区域c 在经济活动p 上具有优势。
定义二值优势矩阵:

对M 的边际加总,代表同时出现在一个区域的不同经济活动数量(经济多样性,diversity)或者某一经济活动出现在的区域数量(经济普遍性,ubiquity)。
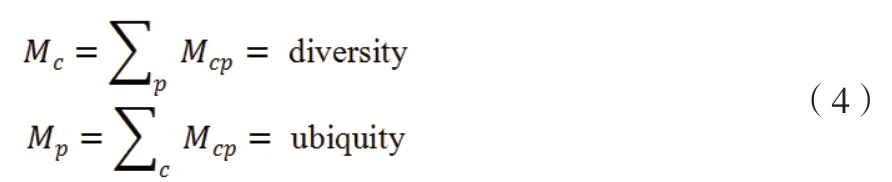
关于测度经济复杂性某个区域c 的复杂性Kc、某个经济活动p 的复杂性Kp,我们认为两者间是互相构成函数关系的。

将函数f,g 设为简单平均,可得到的指数即是经济复杂性指数(ECI;Kc)和产品复杂性指数(PCI;Kp)
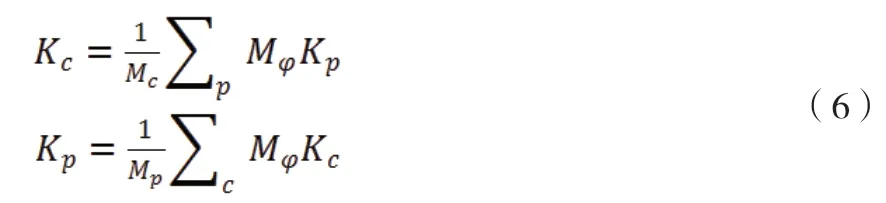
为消除常数项,通过z 变换将经济复杂性归一化处理,得到指数:

这样就得到了经济体的经济复杂性指数ECI 和产品的产品复杂性指数PCI。
通过以上求解过程,我们可以认识到两种复杂性指标的构建过程更多是单纯利用“经济活动——位置”的网络对应关系刻画复杂性,基于无权重的平均化过程通过经济系统的结果计算复杂性指数,这种算法的优势在于普适性较强,形式简洁,但平均化的过程同时也会削弱出口带来的多样性信息特征,对经济复杂性的表征现实能力有一定的削弱。
(三)适应性复杂度算法
针对使用反射法(Method of Reflection)测度经济复杂性算法的不足,Tacchella 等(2012)使用非线性迭代耦合的方法构建了适应性复杂度算法(Fitness and Complexity Algorithm),通过测度国家适应性Fitness 和产品复杂性Complexity 来刻画经济复杂性[4]。
Tacchella 等认为Hidalgo 等提出的经济复杂性ECI 指标体系存在以下不足。首先,ECI 指数使用非加权平均的算法,这使得国家的出口多样性的信息无法在ECI 中体现;同时由于复杂产品和简单产品在算法中享有同样的权重,故出口复杂产品背后象征的高端生产能力也无法有效在ECI 中体现。为解决以上缺陷,适应性复杂度算法构建Fitness 适应性指标来衡量经济体的经济复杂性,Complexity 复杂性指标来衡量产品的复杂性。它的主要改进机制为:使用非线性的迭代耦合算法,改善不同经济复杂性和产品复杂性之间的权重关系。适应性复杂度算法如下所示。算法分两步进行迭代,首先设置Fitness 与Complexity 两变量的初始值均为1,计算出它们的中间变量,之后对两变量进行均一化处理,之后进入下一轮迭代过程。对于Fitness 指标来说,它与使用Complexity 加权的出口多样性成正向关系;对于Complexity 来说,它与产品出口的优势国家数量呈反方向变动,表示如果大部分国家都能够出口此产品,意味着该产品复杂性较低。在Complexity 的算法中,经济体Fitness 在分母求累加的过程中是以倒数的形式存在,这样可以表达复杂性高的经济体对产品复杂性的贡献和影响较弱这一机制;同时分母的累加项最后求倒数这一数学形式表达了产品复杂性和出口它国家的数量呈反方向变动这一经济含义。适应性复杂度构造如下:
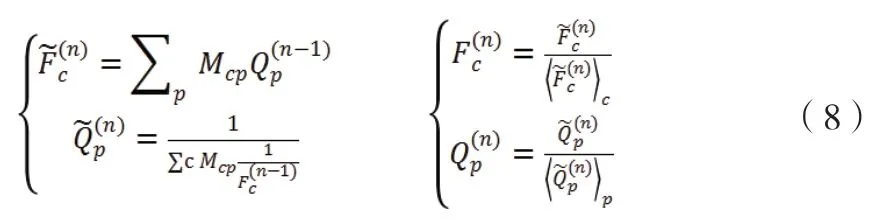
(四)ECI+
对于经济复杂性的测度问题,Albeaik(2017)基于产品空间理论和ECI 指数的思想,构建了ECI+指标来衡量经济体的经济复杂性。ECI+引入经济体的出口量来表达经济体的经济复杂性,而不是反射法中构造指数表达复杂性[5]。它使用经济体出口每一种产品的“困难”(difficult)程度修正出口额度,加总构成ECI+指标。

此时定义ECI+为经“困难”程度修正后的出口总额减去一国出口的平均份额:

在此过程中,为保证数值的收敛性,每一步的Xc都需要进行均一化处理,处理方式如下:

求PCI+的过程与以上过程类似,最终可得:
与上文提到的ECI 经济复杂性指数和Fitness 适应性经济复杂性不同,ECI+的测度体系以出口额为核心,是出口数额的函数,因此是一系列连续的变量,并且能将所有产品的信息利用起来。而无论是ECI 还是Fitness 的算法,需要对数据进行离散化处理,这种离散化的处理方式无疑会随着设定阈值的变化影响研究结果,在识别优势产品的过程导致误差出现。另外未被识别为优势出口产品的产品将不会被计入测度过程中。
三、结语
在中国经济进入高质量发展的今天,经济增长速度已不是我国经济发展的唯一目标,我国经济除了追求量的提升外,更加注重质的提升,而产业结构与经济复杂性特征的演变对我国经济高质量发展与长期增长都尤为重要。产品空间网络理论从产业异质性和复杂性方面,提供了一个对产业结构重新审视的新视角,可以帮助我们对中国产业结构和全球产业网络进行更深入的探索,寻找中国产业结构演变的规律,为我国经济高质量发展提供参考。
引用
[1]Hidalgo C A,Klinger B,Barabási A-L,et al.The product space conditions the development of nations [J].Science,2007,317: 482-487.
[2]Hausmann R,Hwang J,Rodrik D.What you export matters [J].Journal of Economic Growth,2007,12(1): 1-25.
[3]Hidalgo C A,Hausmann R.The building blocks of economic complexity [J].PNAS,2009,106(26): 10570-10575.
[4]Tacchella A,Cristelli M,Caldarelli G,et al.A new metrics for countries’ fitness and products’ complexity [J].Scientific Reports,2012,2: 723.
[5]Albeaik S,Kaltenberg M,Alsaleh M,et al.Improving the economic complexity index [EB/OL].Quantitative Finance,2017-07-18[2020-12-02].https://arxiv.org/abs/1707.05826.

