推广的Su-Schrieffer-Heeger模型的拓扑相图及其表征拓扑相的有限尺度能谱和边界模
杜 涛,李跃勋,陆赫林,章 晖
(云南民族大学 电气信息工程学院,云南 昆明 650500)
拓扑不变量是拓扑绝缘体[1-3]拓扑相的表征量;虽然有不同类型的拓扑不变量,如陈数或TKNN数[4]、Z2拓扑不变量[5]等,但其本质上都来源于固体体能带的不为零的Berry相[6].若系统的拓扑相(包括拓扑平庸和非平庸相)的拓扑不变量发生了变化,则称系统发生了拓扑相变.体能带是固体系统在周期边界条件即考虑系统是无限大且具有平移对称性的情形下得到的在布里渊区上的关于动量(或波矢)与能量的所谓色散关系,因此反映的是固体的内部或块的性质.如果要研究固体系统的边界性质,需要使得所考虑的固体系统成为一个有限尺度系统,此时的边界条件成为开边界条件.在开边界条件下,系统的平移对称性破缺,动量或波矢不再是好量子数,我们得到的将不再是体能带而是系统的有限尺度能谱.对于在开边界条件下具有不平庸拓扑属性的固体系统,虽然不能由体能带给出其拓扑不变量,但这类固体系统的非平庸特性依然存在,其必然表现在它们的有限尺度能谱上.另一方面,由于体——边对应原理(bulk-edge correspondence)[7],由拓扑不变量表征的这类拓扑固体系统的非平庸特性必然体现在其有限尺度系统的边界上.基于以上两点,我们可以反过来考虑,即利用系统的有限尺度能谱和边界模来表征这类固体系统的不同的拓扑相以及进一步地,由他们的变化来揭示系统的拓扑相变.
拓扑固体系统的一个较为简单的模型是一维Su-Schrieffer-Heeger (SSH) 模型[8],其具有不为零的Zak相[9]——特指参数空间为布里渊区的Berry相.一维SSH模型的提出最初是用来解释聚乙炔材料中的孤子激发,并未涉及其具有的拓扑物性.当拓扑绝缘体的研究成为热点后,这一模型随即成为了拓扑绝缘体研究的典型对象[10].目前的一些研究已经推广了这一模型并得到了其较为复杂的拓扑相图[11-15].业已证明[16],一维SSH模型中若其哈密顿量中含有超越紧束缚项的长程电子跳跃项,系统将存在具有更大拓扑不变量的拓扑非平庸相.本文研究的第一个目的是欲在空间维度及长程电子跳跃方面推广原有的一维SSH模型,即考虑两条耦合的具有长程电子跳跃的SSH链.目前这一推广模型还没有人对其做详细讨论,我们的研究将较全面地揭示其具有的较大拓扑不变量的拓扑非平庸相和其较为复杂的相图,为更高空间维度上的推广的SSH模型在其拓扑相、拓扑相变乃至可能存在的高阶拓扑绝缘体相等方面的研究提供一定的基础.第二个目的是想从有限尺度能谱和边界模的视角来研究该系统的拓扑相及相变,并对其进行表征.因为对于一些高阶拓扑非平庸相,如拓扑壁角态 (topological corner state)[17], 其只存在于有限尺度系统中,我们的研究希望能使得这一研究视角可以为这类高阶拓扑非平庸相的讨论提供一些值得借鉴的参考.
1 推广的Su-Schrieffer-Heeger模型及其拓扑相图
1.1 具有长程电子跳跃项的SSH耦合链
最简单的一维SSH模型(下文中称之为基本的SSH模型)为一维晶格上只含最近邻电子跳跃(hopping)项且其强度强弱交替的紧束缚电子模型.由于这一电子跳跃强度的排列,该模型的晶格结构含两套子晶格,即一个晶格原胞中包含有两个晶格格点.当原胞间的跳跃强度大于原胞内跳跃强度时,模型为拓扑绝缘体,其拓扑不变量由不为零的Zak相给出.反之,模型为普通绝缘体,其Zak相为零.原胞间的电子跳跃强度和原胞内的电子跳跃强度相等即为一个拓扑相变点;此时的SSH模型为最简单的单原子链上的紧束缚电子模型,且其体能带的能隙闭合.我们推广这一模型使之包含两个保证系统手征对称性的第三近邻电子跳跃项,并且在空间维度上将其扩展,将两条这样的SSH链耦合起来.推广后的模型的哈密顿量为:
(1)


图1 推广的SSH耦合链的晶格结构
红色框表示一个原胞,晶格常数为a.A,B,C,D分别标记4个子晶格,电子跳跃强度及链耦合强度已标记于图中.
H=ψ†Hkψ.
(2)

在下塘电站岩体附近施测的5线综合物探剖面较明显地反映出F2、F3断层和已知银铅锌矿体的存在(图4、6),矿体产于高、低阻急剧变化的F3断裂带上,CSAMT剖面较清晰地显示出深部高阻隐伏岩体和低阻隐爆角砾岩的空间形态,隐伏岩体主体埋深均在-300m标高以下,隐爆角砾岩呈陡产状产于F2和F3断裂之间。
(3)
其中ρ(k)=(t+δt)+(t-δt)e-ika+t12eika+t21e-i2ka=|ρ(k)|eiφ(k).该哈密顿量(矩阵)可解析得到其本征值为E=s1|ρ(k)|+s2λ的本征矢量:u=(1/2)(1,s1e-iφ(k),s2,s1s2e-iφ(k))T,其中,s1,s2=±1.本文中,将用(s1,s2)来标记这4个本征态或能带.将要讨论的推广的SSH耦合链的拓扑性质将决定于能带的本征波函数在布里渊区上具有的非平庸的Berry相.需要强调的是,这里的本征矢量u的表达式是在SSH链之间的耦合强度λ不是很大的情况下得到的.对于大λ极限,能带的色散即带宽可忽略不计,相应能带的本征矢量将越来越与波矢无关,这将导致平庸的Berry相,从而使得系统的拓扑属性消失.因此,本文讨论的范围仅限于SSH链间的耦合不是特别大的情况.我们是在系统能带具有潜在的拓扑结构的前提下,研究长程电子跳跃对系统拓扑属性的影响.
1.2 拓扑相图
推广的SSH模型的拓扑属性来源于其被电子占据的能带所具有的不平庸Zak相,Zak相的定义为[9,18]:
(4)
其中,um为模型布洛赫哈密顿量(矩阵)的本征值为Em的本征矢量,即第m能带的本征矢量;式中的求和遍历被电子占据的能带.由式(3)的本征问题解,可直接计算得到Zak相,其结果为:
(5)
其中Nocc为被电子占据的能带数目.由Zak相γ的计算可得到模型在参数δt,λ,t12和t21的不同范围内具有的拓扑平庸或不平庸相,相边界由如下方程所决定:
2δt-t12+t21=0,
(6)
2t+t12+t21=0,
(7)
t21[(t+δt)-t21]=t12[(t-δt)-t12].
(8)
从该组方程来看,SSH链之间的耦合并不影响模型的拓扑属性(正如上一小节最后所述,这是在链间耦合强度λ不大的前提下来说的).虽然链耦合不影响相边界,不过其仍会影响系统的能量分布,下一节中将会讨论其在系统有限尺度能谱上的影响.
由相边界(6)式~(8)式及Zak相的计算,可得到推广的SSH耦合链的拓扑相图.在基本的SSH模型即t12=t21=0的情形下,如在上一小节中所述,δt=0为其拓扑相变点.当δt>0时,系统处于Zak相为零的拓扑平庸相;当δt<0时,系统处于Zak相不为零的拓扑非平庸相.在引入长程电子跳跃后,系统将具有丰富的拓扑相和更复杂的相图.模型在δt的三种情形下在t12-t21参数空间中的相图如图2所示.在此处及以后的计算中,我们将参数t设定为归一化因子,并令其为1,作为系统的能标.相图中Zak相γ的取值都是在电子占据为半满即Nocc=2的情形下得到的.
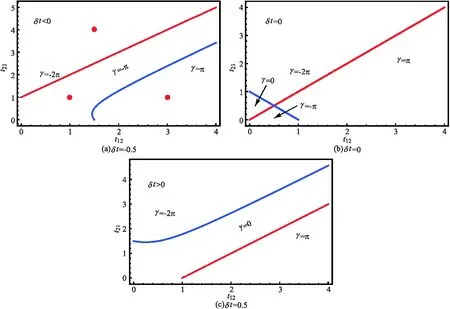
图2 推广的SSH耦合链的拓扑相图
相图只考虑了参数t12及t21都不为负的情形.因此,式(7)所给出的相边界并不在此处给出的相图中.
2 有限尺度能谱及边界模
上一节我们在周期边界条件下得到了模型的四个能带,并通过计算能带的Zak相得到了包含大拓扑不变量的拓扑非平庸相在内的拓扑相图.对于开边界条件或者考虑模型在有限尺度晶格上的情形,相图中不同的拓扑相将会对应着不同的有限尺度能谱结构.另外,由体——边对应原理,系统不同的体或块性质(由拓扑不变量体现)对应着不同的边界属性,我们应该可以得到不同的拓扑相具有的边界模.这样,实际上我们就可以用不同的有限尺度能谱和边界模表征不同的拓扑相.对于拓扑相变,上节中我们已经通过Zak相的变化得到了各拓扑相之间的相边界.在本节中,我们将从不同的拓扑相对应着的有限尺度能谱及边界模的变化至少在定性的水平上得到这些相边界.
2.1 有限尺度能谱及能谱能隙中的简并带
2.1.1λ=0情形
采用开边界条件,系统的哈密顿量将在有限尺度的实空间写出,推广的含长程电子跳跃项的耦合SSH链的哈密顿量为:
H=ψ†Hfiniteψ.
(9)
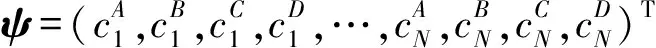
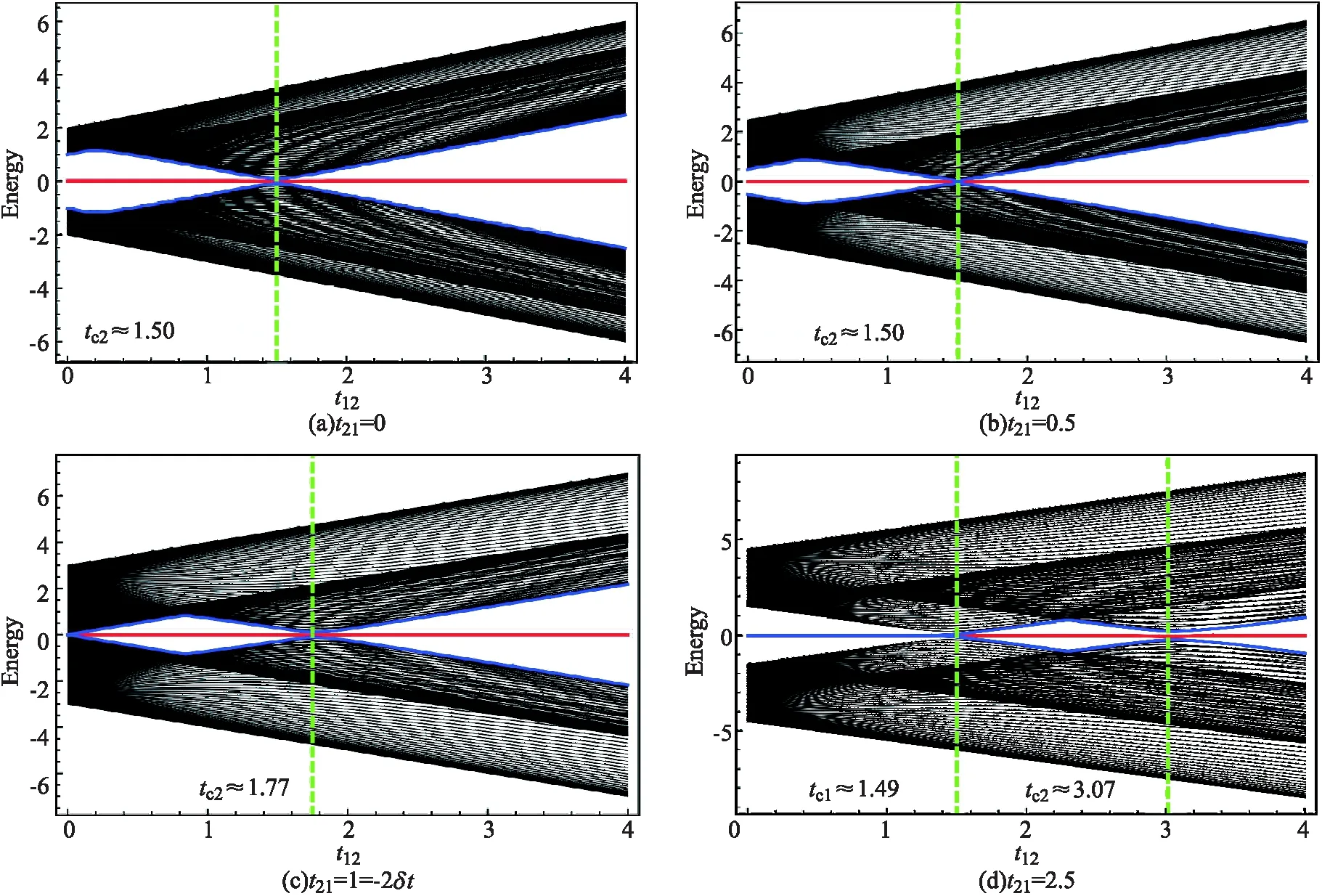
图3 δt<0 (δt=-0.5)情形下两条脱耦SSH链的有限尺度能谱,晶格的原胞数为N=100
基本的SSH模型,当δt<0时其为非平庸的拓扑绝缘体,此时的有限尺度能谱具有能隙,且存在一个表征其拓扑非平庸属性的零能带[10](有必要说一下的是,拓扑平庸系统能谱的能隙中,是不存在零能带的!).在我们的结果中也看到了这一点.图3(a) 的t12=0处的能谱结构正是对应着基本的SSH模型的这一特点.所不同的是地方在于,单链SSH模型中的零能带是二重简并的,而由于我们此时讨论的情况实际上是两条独立的SSH单链,因此我们得到的零能带是由能量为零的第2N-1、第2N、第2N+1和第2N+2带所构成的四重简并带.此时的能谱结构表征着Zak相γ=-π的拓扑非平庸相,其对应于相图2(a)中的点(t12,t21)=(0,0).
对于0≤t21<|2δt|情形(图3(a)、(b)),当t12>0时,系统能隙依然存在,并且能隙中的零能带保持四重简并,这一能谱结构表征的是Zak相γ=-π的拓扑非平庸相,即是位于相图2(a)的中间区域的拓扑相.随着t12的逐渐增大,能隙逐渐减小,最终在t12的临界值tc2处闭合后又重新打开.数值计算结果为:当t21=0时,tc2≈1.50;当t21=0.5时,tc2≈1.50.能隙的闭合与重新打开是发生拓扑相变的重要标志[21-23],因此tc2是一个拓扑相变的临界点.tc2的值与相边界(8)式吻合得很好,同时对比相图2(a),很容易得到此时的tc2其实是从γ=-π的拓扑非平庸相到γ=π的拓扑非平庸相的相变点.于是我们发现能谱在t12>tc2区域的结构表征了γ=π的拓扑非平庸相.该结构的特点是能谱存在能隙且能隙中存在四重简并的零能带.这样,我们发现,在tc2的两侧,相同的能谱结构表征着不同的拓扑相.显然,能谱结构能够部分表征拓扑相,但其实并不充分,我们下一小节将会看到,再加上能隙中的能带所对应的边界模,就可以充分地表征不同的拓扑相了.
当t21=|2δt|时,t12=0是一个特殊的临界值,该取值正好在相边界(6)上(见相图2(a)),此时能隙也是闭合的(见图3(c)).当t12>0时,能谱能隙打开且存在四重简并的零能带.这样的能谱结构与0≤t21<2δt情形一样,表征的是γ=-π的拓扑非平庸相.同样地,在t12=tc2处(此时的tc2约为1.77),能隙闭合后又重新打开,是一个拓扑相变点.而tc2的值与式(8)吻合得很好,因此其是从γ=-π的拓扑非平庸相到γ=π的拓扑非平庸相转变的相变点.于是,能谱在t12>tc2区域的结构同样表征的是γ=π的拓扑非平庸相.问题依然是若以tc2两侧的能谱结构分别来表征γ=-π的拓扑相和γ=π的拓扑相是不够充分的.
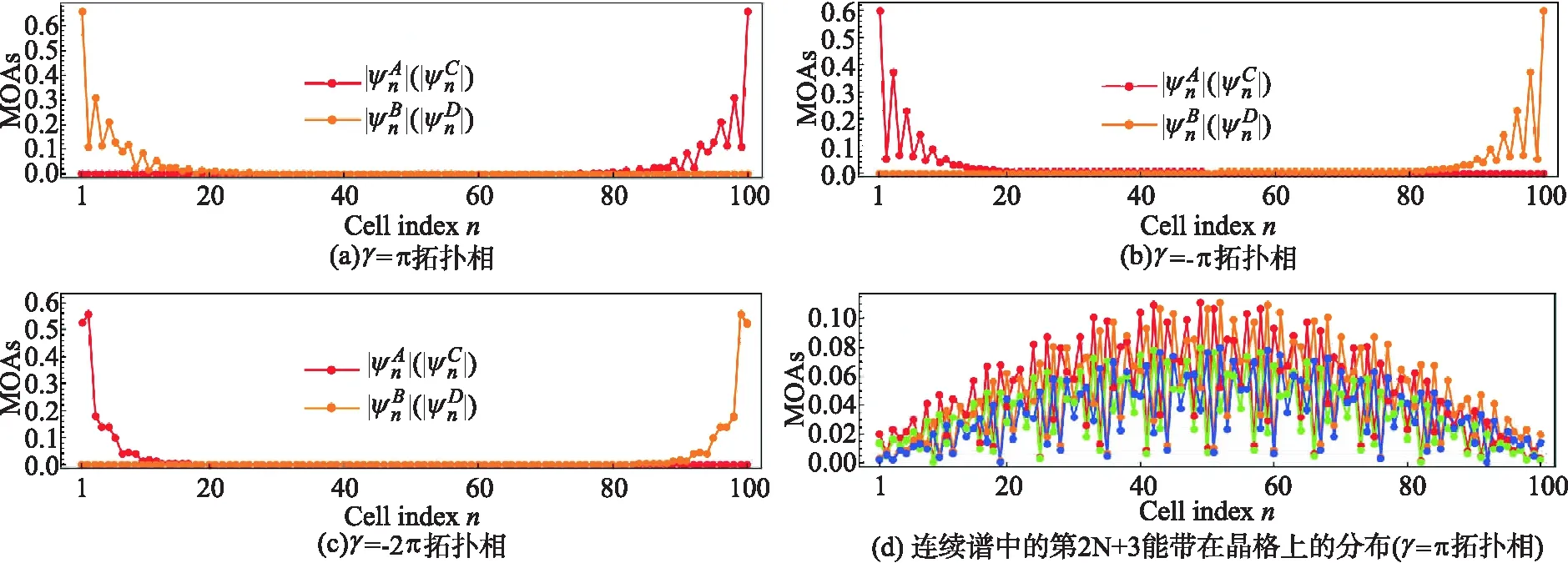
对于t21>|2δt|的情形(图3(d)),将出现两个t12的临界值使得能谱能隙闭合后又重新打开.当t12 2.1.2λ≠0情形 虽然脱耦的两条SSH链的有限尺度能谱已可作为耦合的SSH链的各拓扑相的特征能谱,并且也可从这些有限尺度能谱的能隙闭合又重新打开的情况得到这些拓扑相之间的拓扑相变点,但考虑链耦合情况下的能谱可以使我们从更多的角度表征拓扑相.图4是两条推广SSH链之间的耦合强度不为零时得到的有限尺度能谱. SSH链之间的耦合没有本质上改变有限尺度能谱.我们发现,能谱能隙闭合随后又重新打开的位置相比于SSH链脱耦的情形并没有发生变化,即t12的两个临界值tc1、tc2保持不变.这一结果是与链耦合λ并不影响系统的拓扑属性这一结论吻合的.因为若tc1、tc2的值随着链耦合强度λ的变化而变化,这将使得各拓扑相之间的相边界与链耦合相关,结果就与式(6)~式(8)矛盾了.链耦合的影响在于其对能隙中的能带的改变.从图4可见,对于每一个拓扑相所对应的能谱区域,原来的能隙中的零能带都发生了劈裂,并且劈裂后的能带都不再是零能带了.由此也可知,能隙中零能带的存在并不是SSH系统具有非平庸拓扑属性的必要条件,虽然大多数情况下确实如此,不过除了本文的例子,也有其他研究表明只需要能隙中存在着能带就能预示SSH系统的非平庸属性了[14-15].由于能隙中零能带的劈裂,这些能隙中的劈裂后的能带的简并度也相应的减半.比如,在之前的讨论中,Zak相γ=-2π的拓扑非平庸相可由八重简并的零能带来表征,而现在的链耦合情形下,则是由一个(或两个)四重简并的非零能带表征了. 图4 δt<0 (δt=-0.5)情形下耦合SSH链(λ=0.3)的有限尺度能谱,晶格的原胞数N=100 考虑到链耦合的情形,现在有两个等价的表征不同拓扑相的有限尺度能谱结构了,即:有限尺度能谱具有能隙且能隙中具有八重简并的零能带或具有四重简并的非零能带(由八重简并的零能带劈裂形成)可表征γ=-2π的拓扑非平庸相;能隙中具有四重简并的零能带或具有二重简并的非零能带(由四重简并的零能带劈裂形成)可表征γ=-π的拓扑非平庸相;而γ=π的拓扑非平庸相也可由能隙中具有四重简并零能带或具有由该四重简并的零能带劈裂形成的二重简并非零能带的有限尺度能谱来表征;拓扑平庸相(γ=0)虽然没有在我们讨论的δt<0的情形中出现,但其对应的是能隙中没有能带的能谱结构.从γ=-π和γ=π的拓扑非平庸相对应的能谱结构可见,仅从能谱结构是不能充分表征拓扑相的. 进一步的数值计算表明,随着链耦合强度的增大,能隙中能带的劈裂加剧.在还不是足够大的耦合强度下,劈裂后的能带将最终“融合”到连续谱中,能隙中的能带消失了.而能隙中不存在能带是拓扑平庸相的特征,这是否说明较小的链耦合将导致从拓扑非平庸相到平庸相的拓扑相变呢?我们前面已经提到,只有链耦合充分大的时候,才能导致拓扑非平庸相到平庸相的拓扑相变.如何理解这一矛盾,或者在链耦合变得较大以及达到充分大的过程中,有限尺度能谱将发生怎样的变化并且拓扑相将如何表征将是我们下一步工作要详细讨论的重点.初步的回答是,有限尺度能谱需要分解为两套子能谱来处理;彼时,用来表征拓扑相的能隙中的简并带将在两套子能谱中分别出现. 一个物理上值得探究也是在表征拓扑相时有用的问题是,当系统处于能谱中某个能带即系统的波函数由该能带的本征矢量给出时,电子在晶格格点上是如何分布的?能带的本征矢量在第i个晶格格点上的振幅(振幅的平方即为电子分布的概率密度)为: ψi(m)= (10) 图5 耦合SSH链处于不同拓扑相时能隙中的简并带对应的边界模. 对于γ=π的拓扑非平庸相,我们选择相图2(a)中的点(t12,t21)=(3,1)(相图中的红点)在链耦合的情形下做具体计算.结果表明,该拓扑相能谱能隙中的两个劈裂的能带都分别对应着一个由图5(a)所示的边界模.该边界模的模式为:电子集中分布于耦合SSH链最左边的子晶格B、D和最右边的子晶格A、C上.这其实是长程电子跳跃t12在各电子跳跃包括链耦合竞争中占主导优势的模式.长程电子跳跃t12在完全绝对优势的极端情形下电子在晶格上分布的键图像以及实际计算得到的电子分布情况分别如图6(a)、(b)所示.为了物理图像上更好地理解边界模,我们选择连续谱中的第2N+3带来计算其电子在晶格上分布,如图5(d)所示.显然,从电子在四个子晶格上的分布来看,其大概率地分布于耦合SSH链的中间区域,这样的电子分布就不构成一个边界模. 对于γ=-π的拓扑非平庸相,选择相图2(a)中的点(t12,t21)=(1,1)(相图中的红点)在链耦合的情形下做具体计算.该拓扑相能谱能隙中的两个劈裂的能带所对应着的边界模如图5(b)所示.此边界模的模式与γ=π的拓扑非平庸相的长程电子跳跃t12占主导优势的边界模模式正好相反.此模式为:电子集中分布于耦合SSH链最左边的子晶格A、C和最右边的子晶格B、D上.该模式是原胞间电子跳跃占主导优势时的边界模模式.原胞间电子跳跃具有完全绝对优势的极端情形下电子在晶格上分布的键图像以及实际计算得到的电子分布情况分别如图6(c)、(d)所示. 由得到的这两个拓扑非平庸相(γ=π的拓扑非平庸相和γ=-π的拓扑非平庸相)的能谱能隙中的能带所对应的边界模的结果,我们现在可以完成对这两个拓扑相的表征了.虽然从能谱结构的角度,这两个拓扑相是不能区分的,但他们能谱能隙中的能带所对应的边界模模式是不一样的.因此我们可以得到这样的结论了:至少对于SSH拓扑系统,各个拓扑相可由其有限尺度能谱结构及具有的边界模模式来表征. 对于大拓扑不变量的γ=-2π的拓扑非平庸相,虽然在我们研究的系统中,其已经可由其能谱结构完全表征,不过其具有的边界模亦有与众不同的特征,仍可作为对其的一个表征.选择相图2(a)中的红点(t12,t21)=(1.5,4)在链耦合的情形下做具体计算,该拓扑相能隙中的两个简并带都对应着一个边界模,如图5(c)所示.表面上看来,这个边界模的模式似乎与γ=-π的拓扑非平庸相的边界模模式相似,但其是本质完全不同的分布模式.这种模式实际上是长程电子跳跃t21占主导优势的边界模模式.当长程电子跳跃t21在竞争中具有完全绝对优势时,电子完全分布于耦合SSH链的最左边的两个原胞的子晶格A、C上和最右边的两个原胞的子晶格B、D上.该极端情形下边界模在晶格上分布的键图像以及实际计算得到的电子分布情况分别如图6(e)、(f)所示. 图6 极端情形下边界模的键图像及其电子分布的概率密度值 最后,正如我们前面一直在重复强调的,链间耦合并不影响系统的拓扑属性,而边界模(模式)此时是拓扑相的一个表征(在某些情况,如表征γ=-π的拓扑非平庸相和γ=π的拓扑非平庸相,其是必要的表征),那么链耦合的变化就不应该影响拓扑相的边界模模式.刚刚我们是在具有链间耦合的情况下得到了表征拓扑相的边界模(模式)(见图5),图7是我们得到的不考虑链间耦合时,各拓扑相具有的边界模.可以看到,能谱能隙中的能带(现在是简并度加倍的零能带!)仍然对应着一个边界模且边界模的模式相比于有链间耦合时的模式并没有变,只是电子在晶格上的分布有量的微小变化. 图7 脱耦SSH链的不同拓扑相的能隙中的简并零能带对应的边界模 通过计算含长程电子跳跃项的耦合SSH链的体能带的Zak相,可得到该模型拓扑相的相边界和完整相图.两个重要的结果是,长程的电子跳跃可诱导出具有大Zak相的拓扑非平庸相和理论上不是无穷大的SSH链间的耦合并不影响系统的拓扑属性. SSH拓扑系统的拓扑相可由系统在有限尺度晶格上的能谱结构以及能隙中的能带所对应的边界模完全表征.有限尺度能谱能隙中存在一个八重简并的零能带(链脱耦情形)或两个劈裂的四重简并的非零能带(链耦合情形)以及能隙中的能带对应的边界模模式为长程电子跳跃t21主导的模式表征的是γ=-2π的拓扑相.能隙中存在一个四重简并的零能带(链脱耦情形)或两个劈裂的二重简并的非零能带(链耦合情形)以及能隙中的能带对应的边界模模式为原胞间电子跳跃主导的模式表征的是γ=-π的拓扑相.能隙中存在一个四重简并的零能带(链脱耦情形)或两个劈裂的二重简并的非零能带(链耦合情形)以及能隙中的能带对应的边界模模式为长程电子跳跃t12主导的模式表征的是γ=π的拓扑相.能隙中不存在能带且所有能带都没有对应到边界模表征的是γ=0的拓扑(平庸)相. 在链间耦合强度λ较大的情形下,系统有限尺度能谱蕴含着子能谱结构,这种情况下的系统的拓扑相如何表征是一个值得进一步研究的课题.同时,大λ极限下系统的拓扑相变以及有限尺度能谱结构目前并不清楚,是否存在一个大λ极限下的等效模型是下一步需要明确的问题.当我们推广的SSH模型进一步推广到二维平面时,有限尺度晶格上将存在高阶的拓扑壁角态,目前学界的研究还没有考虑到长程电子跳跃项导致的这种高阶拓扑相的复杂拓扑相变,本文从有限尺度能谱结构及边界模来表征拓扑相的方法,将有助于对拓扑壁角态的表征及系统完整相图的获得.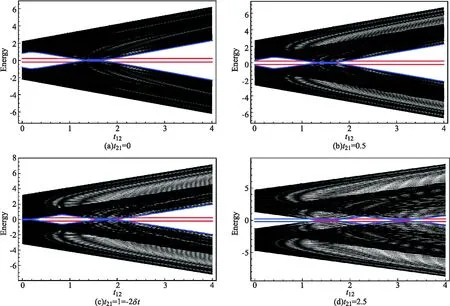
2.2 能隙中的能带对应的边界模
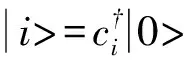


3 结语

