挡墙前有限斜坡土体被动土压力研究*

赵其华 蒋峻峰 郑 涛 彭 毅 王 谊

(①地质灾害防治与地质环境保护国家重点实验室(成都理工大学)， 成都 610059， 中国) (②华南防灾减灾研究院(深圳)有限公司， 深圳 518001， 中国)

0 引 言

有限斜坡岩土体广泛存在于河道斜坡上的桩板墙、基坑中半逆作法施工条件下的围护桩墙、半挖半填路堑边坡上桩板墙等挡墙工程中。这些条件下挡墙前的有限斜坡岩土体，由于受斜坡坡度、挡墙与斜坡边缘距离等因素的影响，导致此种条件下的土体破坏模式与侧土压力分布特征同半无限空间条件下有较大不同(Hu et al.，2020)。因此，挡墙前有限斜坡土体能否提供足够的被动土压力，对准确确定有限斜坡土体中挡墙的稳定性具有重要意义。

目前被动土压力的研究多以半无限空间条件为研究前提。在被动土压力的试验研究方面，国内外众多砂土的被动土压力的室内试验与原位测试结果表明(Clough et al.， 1991； Fang et al.，1994； 顾慰慈， 2001； 徐日庆等， 2002； Becker et al.，2006； 赵建军等， 2019)，当墙体平移时，在半无限空间中的被动土压力大致呈三角形分布，当在墙体绕墙脚转动和绕墙顶转动模式下，被动土压力随深度呈现出较强的非线性分布。试验测试结果与经典的Rankine理论与Coulomb理论中的土压力随深度呈线性分布的特征存在矛盾之处，因而一些学者根据试验监测结果，在静力极限法(Jiang et al.，2021)、图解法(顾慰慈， 2001)、应力状态法(朱建明等， 2015)、水平层分析法(王元战等， 2006)、有限元法(张建勋等， 2004； Liu et al.，2020； 史克宝等， 2020； 赵亮亮等， 2020)等方法的基础上提出了较多关于半无限空间的被动土压力的改进计算理论，主要有对数螺旋线滑面被动土压力计算(Terzzghi et al.， 1996； 顾慰慈， 2001)，考虑土拱效应的被动土压力计算(Hu et al.，2020)，侧向有限土体中的被动土压力计算(韩同春等2018； 徐日庆等， 2020； Chen et al.，2021)，弹性地基梁法(陈继彬， 2017)，应变楔形体计算模型(Ashour et al.，2004； Nimtyongskul et al.，2018； 杨明辉等， 2019)，考虑位移影响的非极限被动土压力(Ni et al.，2018)等。对有限斜坡岩土体中的被动土压力研究，应宏伟等(2011, 2016)采用室内模型试验和数值模型研究了土体有限侧限宽度对被动土压力的影响，但并未考虑斜坡坡度与临坡距影响。Nimtyongskul et al. (2018)、Yin et al. (2018)和喻豪俊等(2018)则是研究采用原位试验或数值模型研究了斜坡坡度对水平受荷单桩的侧向地基承载力与地基反力系数分布特征的影响，并对半无限空间的水平受荷单桩侧向极限承载力公式进行了改进。Muraro et al. (2014)和Pirone et al. (2018)采用强度折减法研究了斜坡条件下单桩加固坡体后的桩位移、被动土压力与结构内力分布特征。

由上述被动土压力的研究现状可见，考虑斜坡坡度、临坡距及土层内部剪力的被动土压力的理论计算仍不多见，而目前实际工程中，斜坡条件下挡墙前有限土体的被动土压力的计算仍多采用传统的半无限空间的土压力理论进行折减计算，由于忽略了斜坡坡度、临坡距等因素对侧土压力的影响，导致传统的被动土压力计算理论在斜坡有限土体中的计算误差较大，进而因水平抗力不足而出现挡墙倾覆或推倒破坏等工程问题，如四川茂县黑虎四村滑坡、三岔湖雷打石滑坡等。针对以上情况，本文采用水平层分析法、静力平衡法与数值模型，研究斜坡坡度、挡墙与斜坡边缘距离以及土条水平层间剪切力等因素对被动土压力的影响，推导了一种斜坡上有限土体中的被动土压力计算公式，用室内与数值模型结果验证了该建议方法的合理性。

1 计算模型

1.1 数值模型

由于影响土压力因素较为复杂，无论是常见的边坡挡墙或是基坑围护结构墙体，现有的众多土压力理论多是基于平动模式下经典的Rankine理论与Coulomb理论，故本文研究以简单的平动模式为基础(应宏伟等， 2011)，采用有限元Midas GTS对挡墙前斜坡土体破坏特征进行研究，将初始位移为0的墙体向左平移600mm，使挡墙(总长16m或20m，墙高H1为8m，嵌入深度L为8m或12m，墙厚0.8m，临坡距b=4m或20.4m)两侧土体达到极限状态，并用强度折减法确定土体最终破坏面位置(Pirone et al.，2018)。二维数值分析模型尺寸及边界条件如图 1。模型计算参数如表 1。网格采用3节点三角形与4节点四边形的混合单元平面网格，单元尺寸为0.5～2.0m。土体破坏服从莫尔-库仑准则。挡墙前斜坡坡度为25°。

已有大量研究表明，位移云图能准确显示土体破裂面的位置(Liu et al.，2020)。图 1中，挡墙前侧土体破裂面均经过墙脚与坡脚附近位置，图1a、图1b和图1c中的破裂角分别为22.6°、7.9°和11°，相比朗肯被动破裂角29°明显偏小，表明斜坡条件的破裂角β≤45°-φ/2； 随着墙体嵌入深度与临坡距的增加，由于受斜坡影响，挡墙前土体并未沿朗肯被动破裂角破坏，而是沿着坡脚附近或坡中最为薄弱的位置出现破坏； 即使临坡距足够大，且满足b/L=cot(45°-φ/2)时，破裂角可能依然沿坡脚破坏，这与半无限空间条件下的被动区土体破坏特征明显不同。

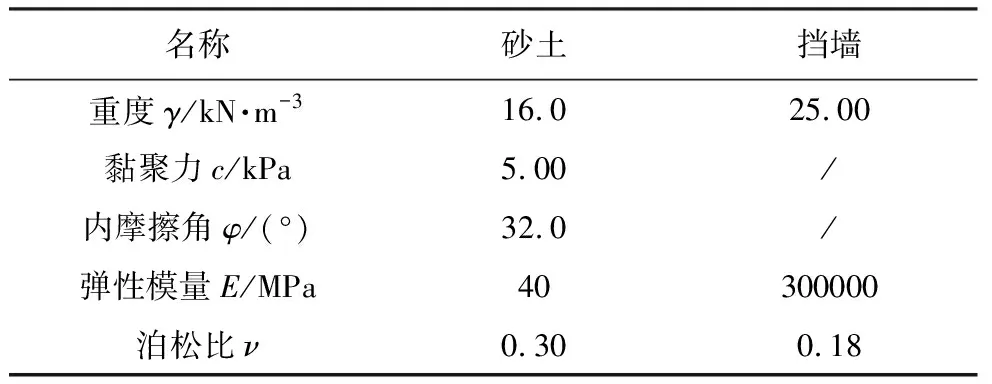
表 1 数值模型计算材料参数Table1 Material parameters in the finite element model

1.2 基本模型建立

图 2中ABCD为挡墙前土体被动区滑移楔形体。挡墙墙高为H1，斜坡坡高为H2，挡墙嵌入深度为L，挡墙前斜坡土体坡度为α，假定破裂面与水平面的夹角为β，A、C点的竖向高度为L1，C、B点的竖向高度为L2，临坡距为b，土条ef与e′f′厚度为dy，土条与AD面的竖向高度为y。

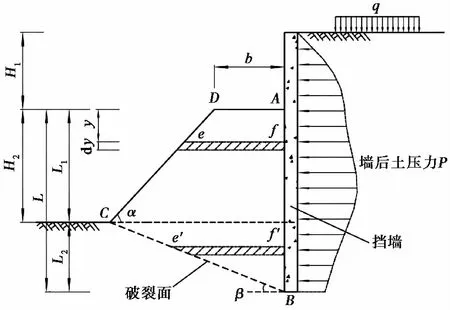
图 2 斜坡条件的土压力计算模型示意图Fig. 2 Sketch of lateral earth pressure calculation for the finite soil in sloping condition

1.3 基本假定

假设： ①模型处于平面应变状态； ②挡墙前有限斜坡土体为均质弹塑性体； ③土体破坏时处于极限平衡状态，并服从莫尔-库仑准则； ④土体破坏面始终经过墙底(Yin et al.，2018)； ⑤挡墙为刚体。

2 基本模型求解

由于ef和e′f′土条边界条件不同，需以C点为边界，分为上下两段0≤y≤L1和L1≤y≤L2，分别对ef和e′f′土条进行受力分析。由于已知L、b、α和β，则：

(1)

2.1 0≤y≤L1 段ef土条受力分析

由图 3，该段墙土接触面f点处的正应力σw均由土条上下界面处的剪应力承担，因此在平动模式下该段仍需要考虑一定的土体剪应力，才能满足静力平衡。令土条顶面上的剪应力与竖向应力之比为层间平均剪切系数K1(王元战等， 2006)，则：

τm=K1σv

(2)

式中：σv为土条上的竖向正应力。

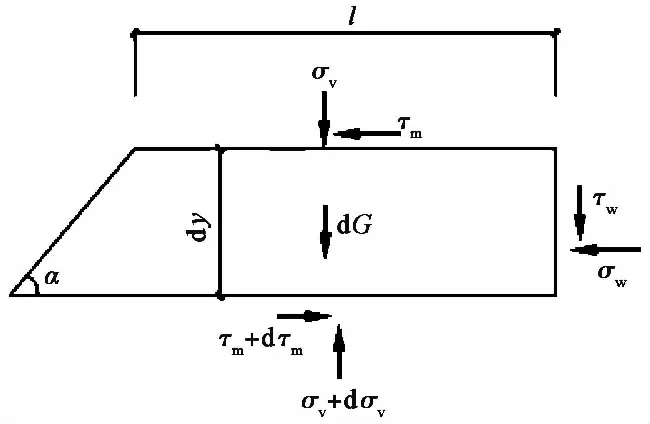
图 3 土条ef受力分析图Fig. 3 Force analysis of ef trapezoidal layer element

假定该段层间平均剪切系数K1与深度呈线性正相关(陈奕柏等， 2015； Hu et al.，2020)，则：

(3)

式中：KC为C点处分界面上层间剪切系数，且L1>0。

2.1.1 墙面粗糙时

根据土条ef在水平与竖向的静力平衡条件，略去高阶无穷小后，可得：

(4)

式中：σw为f点接触面处的正应力；τm为土条水平剪应力；l为土体ef的水平长度，l=b+ycotα； dG=γldy。

由莫尔-库仑破坏准则，墙土接触f点处的剪应力：

τw=σwtanδ+cw

(5)

式中：δ为墙土接触面摩擦角；cw为墙土接触面黏聚力。

联立式(2)、式(4)与式(5)，消除dσv/dy后，则：

(6)

令y=L1，代入上式，可得：

(7)

(8)

式中： 斜坡倾角α≠0°。

上式表明，斜坡条件下的0≤y≤L1段的被动土压力与斜坡坡度、斜坡顶面宽度及土体层间剪切系数密切相关。

由于上式中，k值仍为未知数，后续需通过C点上下界面处的边界条件相同来进行求解。

将式(6)代入式(4)，消去σw，则：

(9)

利用边界条件y=0时，σv=0，求解微分方程式(9)，则得到土条ef上部的正应力为：

(10)

式中： 墙土摩擦角应满足δ≠0°。

当y=L1时，代入式(10)，则C点水平界面处的竖向正应力为：

(11)

2.1.2 墙面光滑时

当δ=0°时，求解微分方程(9)，根据边界条件：y=0时，σv=0，则：

(12)

此时，当y=L1时，代入式(12)，则可得到C点水平界面处的竖向正应力为：

(13)

2.2 L1≤y≤L2 段e′f′土条受力分析

由图 4，平动模式下的墙土接触面f′点处的正应力σw主要由滑动面e′点处的正应力与切应力承担，为简化计算，因此该段将层间剪力忽略(朱建明等， 2015)。

图 4 土条e′f′受力分析图Fig. 4 Force analysis of e′f′ trapezoidal layer element

2.2.1 墙面粗糙时

根据土条e′f′在水平向与竖直方向的静力平衡条件，可得：

(14)

式中：τs和σs分别是破裂面BC上的剪应力与正应力；l为土条e′f′水平长度，l=(L-y)cotβ。

由于土体破裂面BC破坏遵循莫尔-库仑准则，则破裂面上的剪应力为：

τs=σstanφ+c

(15)

式中：c为土体黏聚力。

联立式(6)、式(15)代入式(14)，消去σs、τs与τw，则：

(16)

对土条e′f′上e点取矩，根据力矩平衡∑M=0，则：

(17)

联立式(6)、式(16)和式(17)，消除σw，可得一阶微分方程为：

(18)

式中：

根据边界条件，当y=L1时，C点处边界面上的竖向正应力值即为σC1，求解式(18)，则土条e′f′上竖向正应力为：

(19)

联立式(6)、式(16)和式(17)，消除dσv/dy，则：

(20)

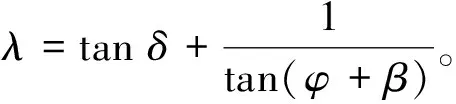
将式(19)代入式(20)，可得水平正应力为：

(21)

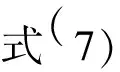
(22)

式中：

当ξ1=0时，则：

(23)

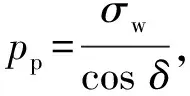
(24)

上式中墙土摩擦角应满足δ≠0°。

上式表明，斜坡条件下的斜坡坡度、临坡距、挡墙嵌入深度等因素仍对L1≤y≤L2段地面以下的被动土压力存在一定影响。

将式(11)和式(24)代入下式，则斜坡条件下作用在挡墙上的土压力合力Q为：

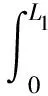
(25)

式中：ζ=ksinδ(γb+cw)+γcotαcosδ。

2.2.2 墙面直立光滑时

当δ=0°时，则τw=0kPa，即墙背直立光滑，同样根据水平与竖向平衡条件，则：

c·cotβ

(26)

再对土条e点取矩，根据力矩平衡，则：

(27)

根据边界条件，求解微分方程式(27)，可得：

σv=γ(y-L1)+σC2

(28)

根据pp=σw，将式(27)和式(28)代入式(18)，则墙面光滑的斜坡条件下的被动土压力为：

(29)

此时，同样联立式(10)和式(29)可得，C点界面处的水平层间剪切系数为：

(30)

2.2.3 挡墙临坡距足够大时

根据图 5，当破裂面BE经过顶面时，此时L1=0m，则有L2=L。将该条件代入式(1)，则需要临坡距满足：

b/L>cotβ

(31)

若E点与D点重合，将L1=0m，L2=L与b=Lcotβ参数代入式(19)中的C1常数公式中： 则：

(32)

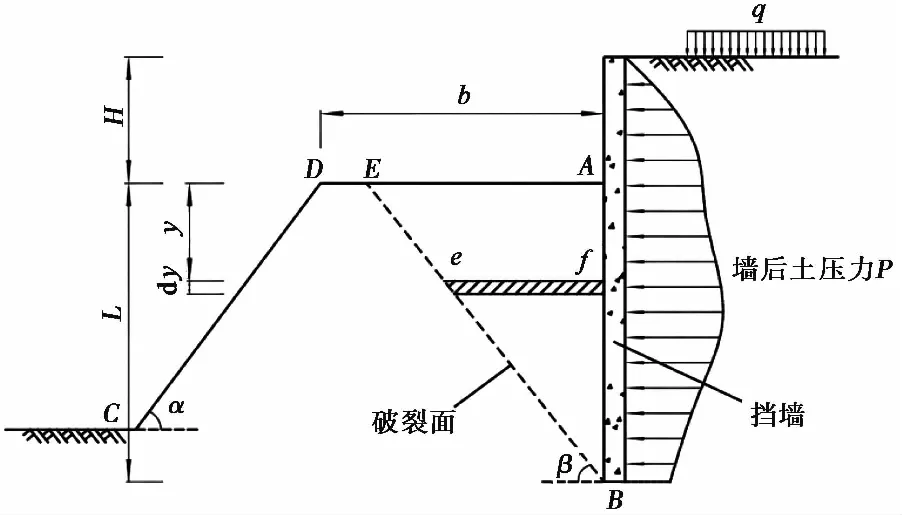
图 5 临坡距足够大时的墙土体破坏Fig. 5 The failure mode of the soil-wall mass when the distance of retaining wall from the crest of slope is enough large

将式(32)代回式(24)，则半无限空间墙背粗糙条件下的被动土压力计算公式。

(33)

若墙背光滑且土体破坏角为朗肯被动破裂角，并将上述条件代入式(29)，则：

(34)

上式即为朗肯被动土压力计算公式。上述计算公式表明，在δ=0°时，式(29)可简化为朗肯被动土压力计算公式。

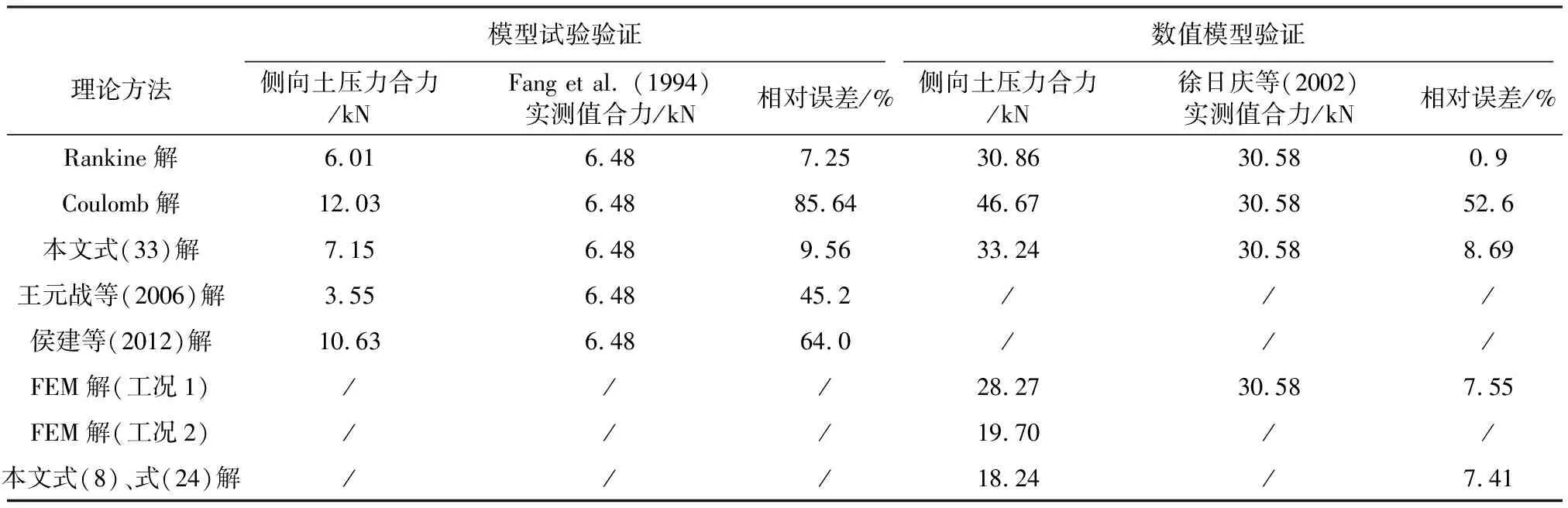
表 2 理论值与实测值对比

3 模型验证

3.1 模型试验验证

Fang et al. (1994)对半无限空间条件下的被动土压力进行了模型试验。墙体通过平移s/L=10%达到极限状态。模型挡墙嵌入深度L=500mm。渥太华砂的具体参数如下：γ=15.5kN·m-3，c=0kPa，φ=30.9°，δ=19.2°，本文解按朗肯被动破裂角。

图 6对本文解与其他理论方法及实测值进行比较，表明平移模式下的被动土压力分布特征随深度逐渐增大，本文解在深度0.6L以上大致呈线性特征， 0.6L以下则呈指数增加趋势，这与实测值存在一定差异，但结合表 2，本文解的被动土压力合力值相比实测合力值偏大，与实测值的相对误差为9.56%，相比其他理论解则更为可靠。

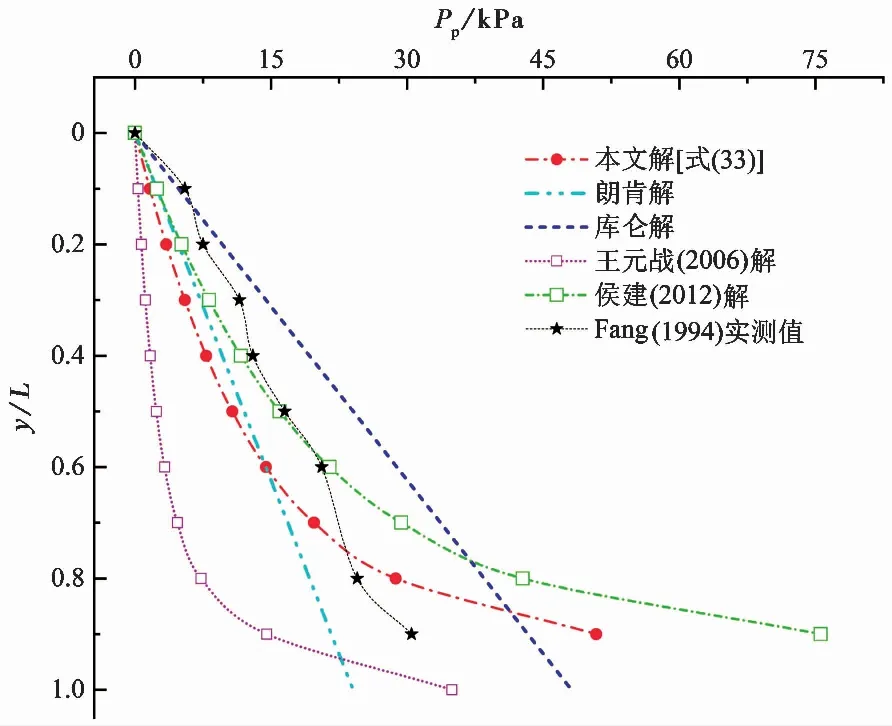
图 6 平移模式下不同理论方法计算与实测值比较Fig. 6 Comparison between predicted and experimental values obtained under translational mode

3.2 数值模型验证

徐日庆等(2002)对砂土中的被动土压力进行模型试验。模型中挡墙嵌入深度L=1.0m，墙厚5cm，墙体通过位移平移法s=50mm，使墙体达到被动状态。在上述室内模型基础上建立二维挡墙数值模型，同样采用3节点三角形与4节点四边形的混合网格，建模具体尺寸及边界条件如图 7，单元尺寸为0.1～0.2m。采用静力非线性分析计算了两种工况：工况1的坡顶为水平条件，本文解按朗肯被动破裂角； 工况2为挡墙后侧土体开挖形成30°斜坡，挡墙距离斜坡边缘b/L=0.2，距离斜坡较近，破裂角经过坡脚β=12°。计算参数如表 3。

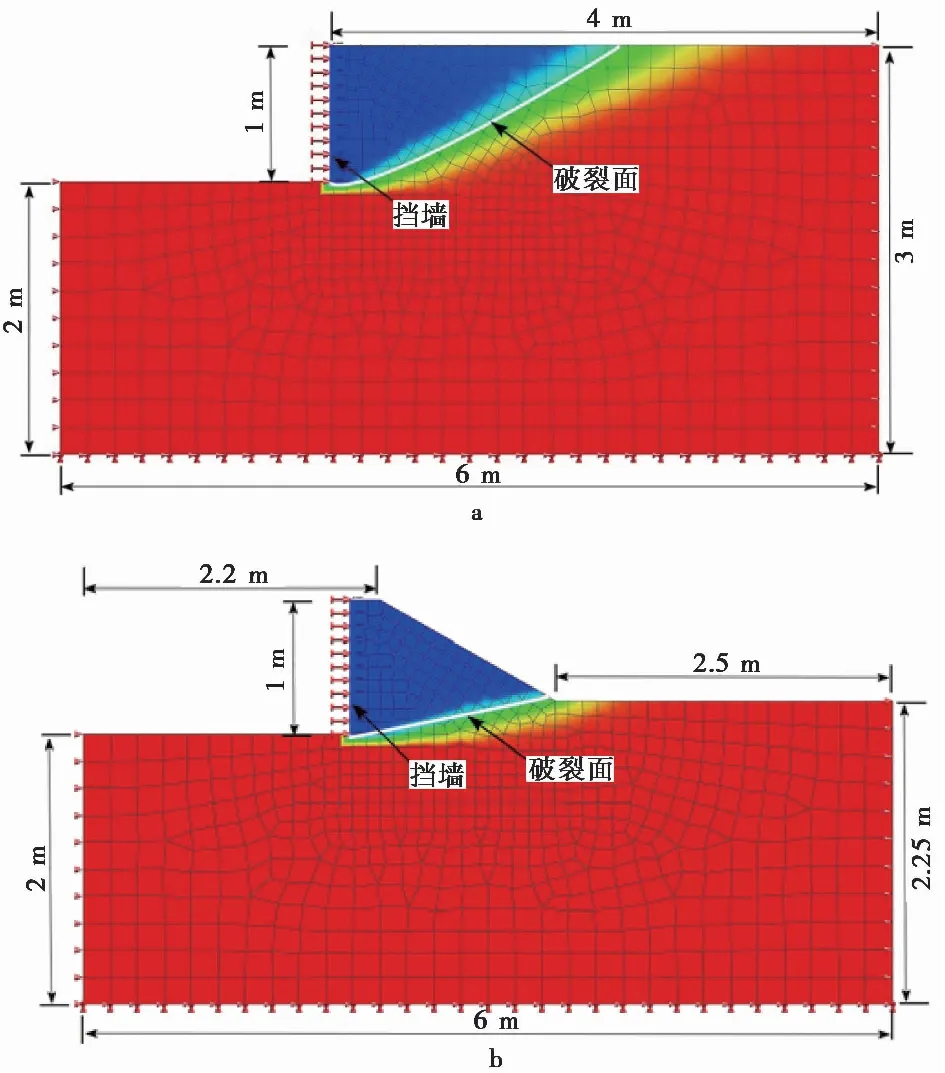
图 7 两种条件下的墙-土体水平位移云图Fig. 7 Horizontal displacement cloud map under two conditions a. 工况1：半无限空间条件; b. 工况2：30°斜坡条件

表 3 数值模型计算材料参数Table3 Material parameters in the finite element model

图 8 工况1条件下的理论值与实测值比较Fig. 8 Comparison between predicted and experimental values obtained under the first condition

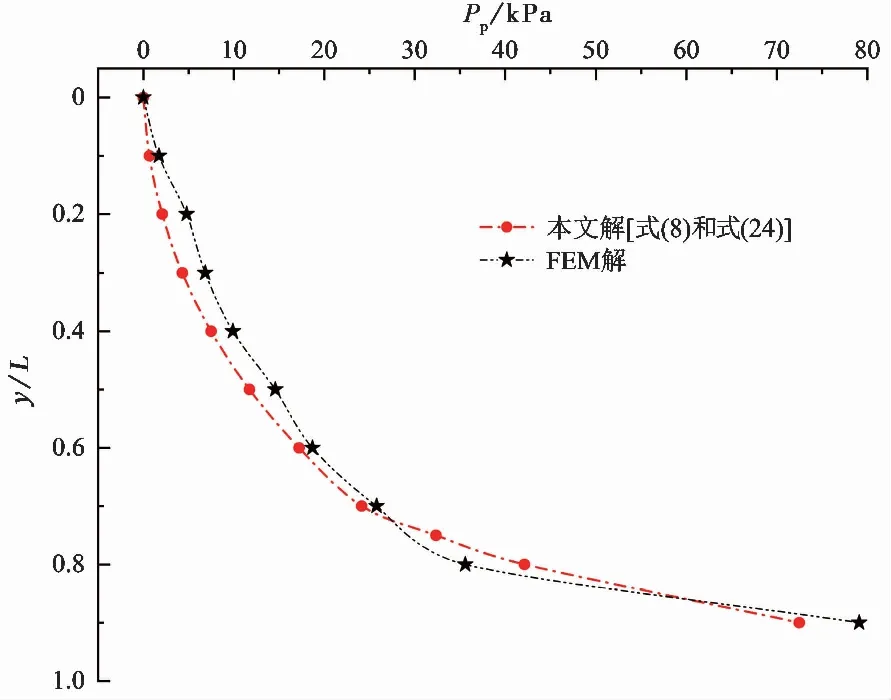
图 9 工况两条件下建议值与数值计算值比较Fig. 9 Comparison between predicted and calculated values of FEM under the second condition

图 7通过对两种不同条件下的位移云图进行对比，再次表明斜坡条件挡墙前侧土体破坏特征与半无限空间条件下的土体破坏特征明显不同。

图 8对工况1条件的理论解、数值解与实测值进行了对比，表明本文解大致介于朗肯解与库仑解之间，结合表 2，朗肯解、本文解及数值解的被动土压力合力值相比库仑解，更为接近实测值。其中数值解的相对误差为7.55%，验证了数值模型参数取值与边界条件的准确性，为工况2的计算提供了依据。

图 9对两工况条件下的本文解与数值解进行比较，表明本文解与数值解基本吻合，斜坡条件下的被动土压力随深度呈指数特征增长。结合表 2中的被动土压力合力值，本文解的相对误差为7.41%，证明了本文解对有限斜坡条件的被动土压力预测的适用性。

4 参数分析

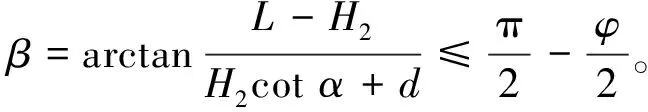
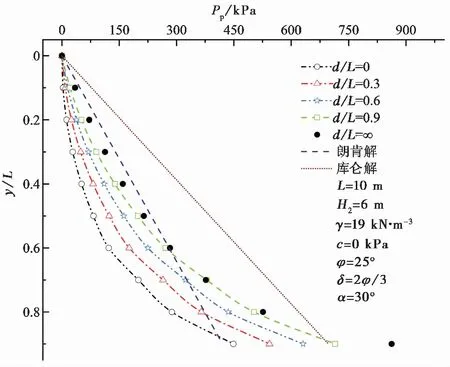
图 10 不同临坡距的被动土压力变化曲线Fig. 10 Distribution of passive earth pressure with the different distance of retaining wall from the crest of slope

图10是被动土压力随临坡距与深度变化的规律。随临坡距增大，斜坡条件下被动土压力也增大，并逐渐趋近于b/L=∞的被动土压力； 被动土压力在斜坡条件下随深度呈指数增加规律。通过计算，朗肯解、库仑解与b/L=0/0.3/0.6/0.9/∞的被动土压力合力值分别为2335.5kN、3871.9kN、1236.85kN、1638.49kN、2010.79kN、2366.71kN和2641.66kN。其中：b/L=0的被动土压力合力相比朗肯解小47%，表明临坡距越小，被动土压力降低幅度较大； 相比Rankine解与Coulomb解，b/L=∞的被动土压力合力与Rankine解更为接近。

图11是不同坡度条件下被动土压力随深度变化曲线。当其他条件不变，随斜坡坡度增加，被动土压力出现逐渐降低现象，α=35°时的被动土压力合力1175.1kN相比α=15°的1795.9kN降低34.56%，但随着坡度增加，被动土压力的降低幅度逐渐趋于平缓。

图12是不同坡度与临坡距对层间剪切系数k的影响关系对比。随着临坡距增加，层间剪切系数k逐渐增大，但增加幅度较小； 当α=10°时，层间剪切系数随临坡距基本呈线性变化； 随着坡度α增大，当挡墙接近斜坡边缘时，层间剪切系数出现较大幅度增大。尽管层间剪切系数会受坡度与临坡距影响，但其变化范围始终在0.05～0.1之间，表明在平动模式下上部临空斜坡土体中的层间剪切系数仍较小。

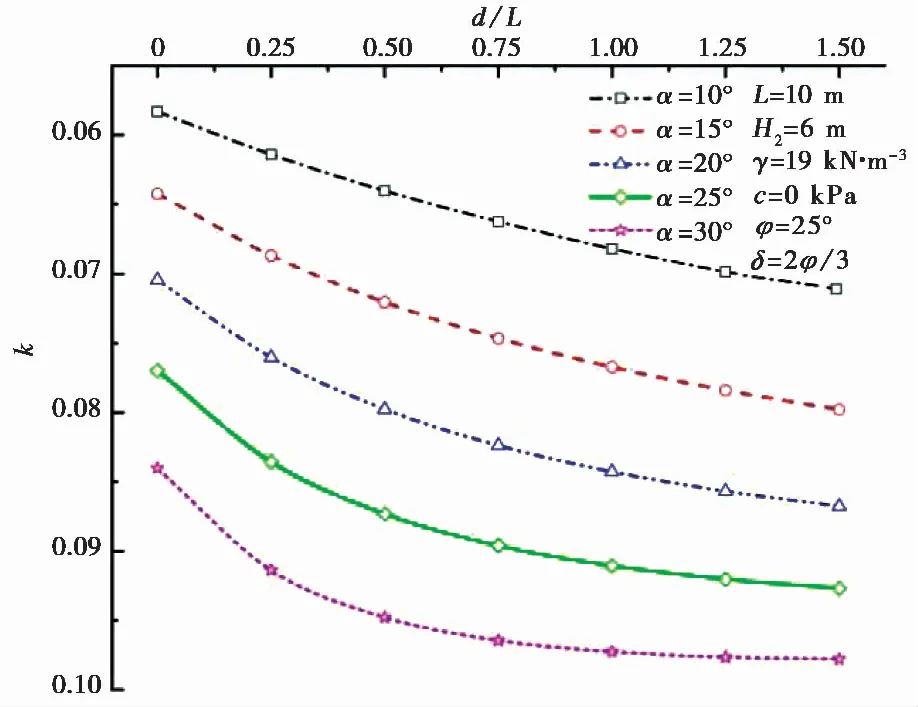
图 12 不同临坡距与坡度的层间剪切系数对比Fig. 12 Coefficient change of the layer shear stress with different distance of retaining wall from the crest of slope

5 结 论

本文采用水平层分析法、静力平衡法及有限元法，推导了一种挡墙前有限斜坡土体中的被动土压力公式，该方法考虑了斜坡坡度、临坡距、土层水平层间剪切系数、墙土摩擦角、黏聚力等因素对被动土压力的影响。通过模型试验、数值模型及其他理论方法验证了本文方法的合理性； 最后分析了斜坡坡度、临坡距对被动土压力与层间剪切系数的影响。主要结论有：

(1)由于受有限斜坡体的影响，平动模式下的挡墙前有限斜坡土体的破裂角一般沿着坡脚附近或坡中的薄弱位置破坏，且破裂角一般满足β≤45°-φ/2，这与半无限空间条件下的土体破坏特征明显不同。

(2)挡墙前临坡距、斜坡坡度对被动土压力的影响较大。斜坡条件下，被动土压力随深度呈指数增加的规律； 当临坡距减小时，被动土压力出现较大幅度减小，其中临坡距为0时，被动土压力相比半无限空间中的被动土压力降低幅度30%～50%。而斜坡坡度增加，被动土压力也出现较大幅度降低，但随着坡度增加，逐渐趋于平缓。

(3)平动模式下挡墙前的临空斜坡土体中的剪切系数较小，主要在0.05～0.1。

(4)当墙背直立光滑且临坡距足够大时，本文建议方法可简化为理想条件下的朗肯被动土压力公式。