基于BP神经网络算法的技能人才模型建立研究

□何玉辉 尹存涛

一、引言

据广元市人力资源和社会保障事业发展统计公报指出截止2018年底，全市专业技术人才达到58,300人，具有高级职称的人才占比10%左右。近年来广元市对人才越来越重视，开展了多批次的人才引进工作，引进了一些领域紧缺急需人才，为引进的人才提供了安家费与工作补助费。近年来，广元市举办了职业技能大赛，对技能人才非常重视。因此依据现有数据，建立系统模型，对技能人才需求进行预测与分析，具有重要的意义。

近年来许多研究人员对这一问题采用多种方法进行了研究。康杰建立了GM(1,2)模型，对四川革命老区达州市进行了人才总量需求预测[1]，同时在人才培养方面提出自己的观点。仇梦华对浙江省高技能人才需求进行了预测[2]，选取了BP神经网络预测模型，基于Python进行了神经网络训练，采用GM(1,1)模型对影响BP神经网络预测模型输出值的影响变量进行了预测，从而作为系统输入，对2018～2030年高技能人才需求进行了预测。

本文在文献调研的基础上，结合广元市统计局、四川省统计局等已知的数据，分析出影响专业技术人才数量的指标，同时根据已知数据，对神经网络进行训练，比较不同的隐含层对神经网络模型的影响，最终确定神经网络模型的输入层、隐含层节点数，并基于Matlab进行程序编写与调试，对2010～2018年技能人才预测值与实际值进行分析。

二、影响指标选择

(一)技能人才数量变化规律。通过对图1技能人才数量总体变化趋势进行分析，从2010年～2018年，广元市技能人才数量逐渐递增，但是不是简单的线性关系。

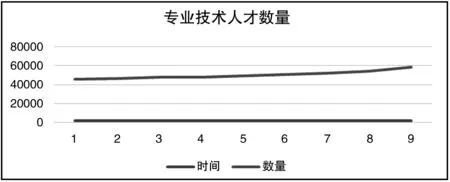
图1 技能人才数量总体变化趋势

(二)回归分析。仇梦华等人，采用回归分析，确定了影响技能人才需求的总体指标，包括GDP、固定资产投资，教育支出、科技支出等。利用SPSS软件，进行回归分析，分析影响技能人才需求的总体指标。

1.教育支出指标分析。利用2010～2018年的教育支出，导入SPSS软件中，利用分析-回归-线性，得到调整后的R^2为0.586[3]。

2.GDP指标分析。利用2010～2018年的GDP数据，导入SPSS软件中，利用分析-回归-线性，选取人才数量为因变量，GDP为自变量，得到调整后的R^2为0.919。

3.其他指标分析。对固定资产投资指标进行分析，选取人才数量为因变量，固定资产投资为自变量,得到调整后的R^2为0.833。

通过以上分析，确定影响人才需求的主要指标包括教育支出、GDP指标、固定资产投资。通过软件分析得到，三项指标作为自变量，人才需求作为因变量，得到调整后的R^2为0.95左右，依照统计学相关知识，说明教育支出、GDP指标、固定资产投资这三项指标对技能人才需求解释力达到0.95左右。

三、BP神经网络模型建立

(一)BP神经网络结构。BP神经网络主要包括输入层、隐含层、输出层，这里假设BP神经网络隐含层只有1层，节点个数待定。由于系统输入有三项指标，教育支出为X1，GDP指标为X2，固定资产投资为X3，隐含层节点假定为4个，由于需要预测技能人才数量只有一个变量，因此输出层，设计1个节点。三层BP神经网络结构如图2所示。

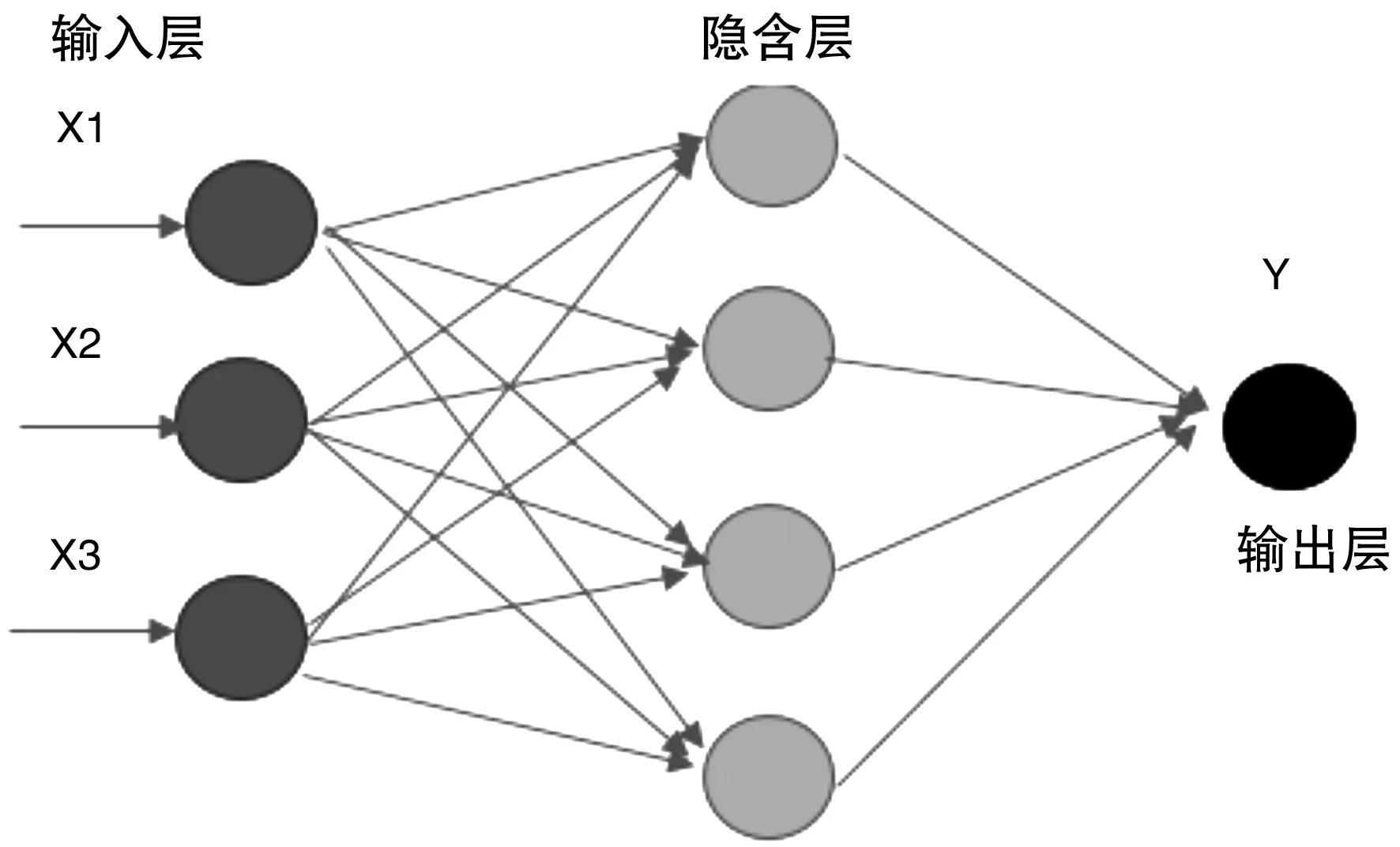
图2 三层BP神经网络结构

(二)数据归一化处理。王小川等人在Matlab神经网络43个案例分析一书中指出[4]，数据归一化是BP神经网络建立的一个重要步骤，常见的方法有最大最小法，平均数方差法。最大最小法公式中，FK为待求值，Xmin为输入序列X1中的最小值，Xmax输入序列X1中的最大值，Xi为输入变量的某一个值。

FK=(Xi-Xmin)/(Xmax-Xmin)

对2010年～2018年的数据进行归一化处理，得到归一化结果，如果后面的值继续增大，可以通过设置Xmax最大值的估计值。

(三)隐含层节点数确定。神经网络隐含层确定的方法主要通过实验来确定[5～7]，通过对比分析，得到结果，但是也有一些经验公式可以利用。

其中X为输入节点个数，Y为输出节点个数，N为隐含层节点个数，A的取值范围为(1，10)。

(四)BP神经网络算法实现方法。输入数据保存在X1、X2、X3中，输出数据保存在Y中，并对数据X1、X2、X3以及Y进行归一化处理，设置一些参数，利用newff函数建立神经网络，调用train训练[8～10]，利用sim函数观察输出值，输出权值与阈值，判断输出的结果是否满足了精度要求，如果达到要求，就停止训练，否则就继续训练。

四、分析与验证

(一)基于Matlab与迈实软件进行验证。以2010～2018年固定资产投资为例，基于迈实软件探索不同的隐含层节点个数与训练次数的关系。假设有一个输入变量时间T。设置网络层数为3，均方差1e-04，通过软件仿真分析得到，隐含层节点数为8时，训练次数为32,252次，可以达到预期要求。尝试不同的隐含层节点数，得到如表1所示，通过分析表1的数据不难得出，对于固定资产投资预测，可以选用隐含层节点数为7，此时训练次数为11,538次。

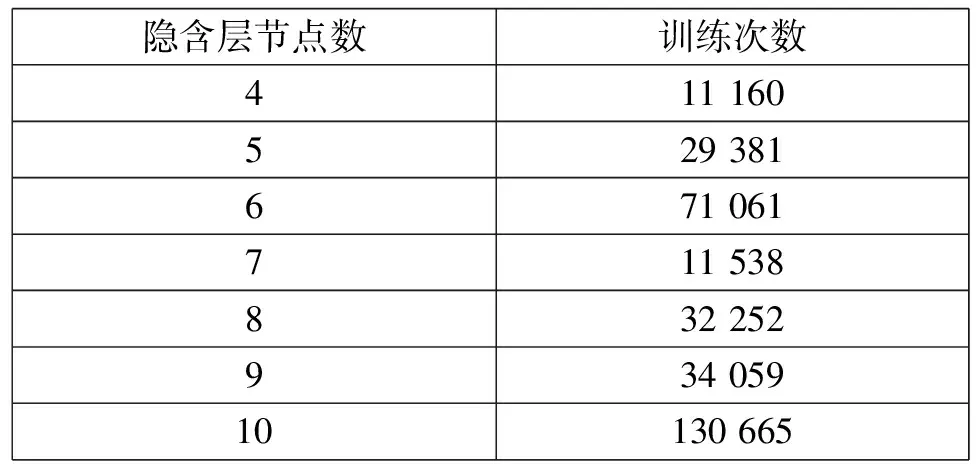
表1 隐含层节点数目对训练次数的影响

基于Matlab实现神经网络算法，将原始2010～2018年固定资产投资数据保存在EXCEL中，利用xlsread读取数据并进行保存，对数据采用mapminmax函数进行归一化处理[11～12]，建立模型，并进行训练与预测，计算目标值与实际值的偏差，如果查找到某次训练目标值与实际值接近要求的误差，则计算结束。基于Matlab编程实现神经网络算法预测值与实际值如表2所示。

(二)利用BP神经网络建立专业技术人才总量模型。按照前面所述，输入层为3个节点，输出层为1个节点，设置精

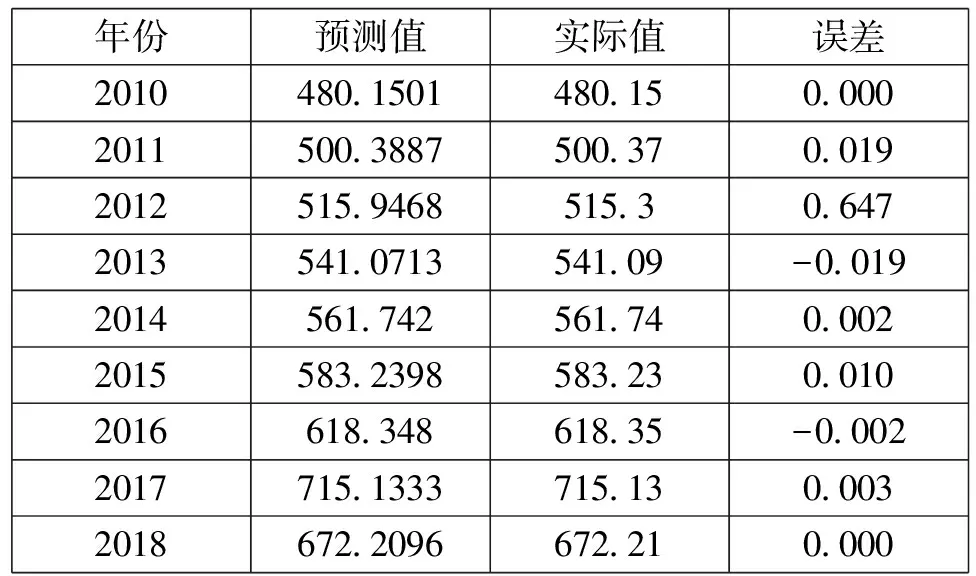
表2 基于Matlab编程实现神经网络算法预测值与实际值

度等指标，建立2010～2018年的神经网络模型。基于BP神经网络模型，结果可能与当年的实际值有一定差距，但是理论上神经网络算法在模型建立方面具有一定优越性。基于BP神经网络建立的专业技术人才模型分析如表3所示。

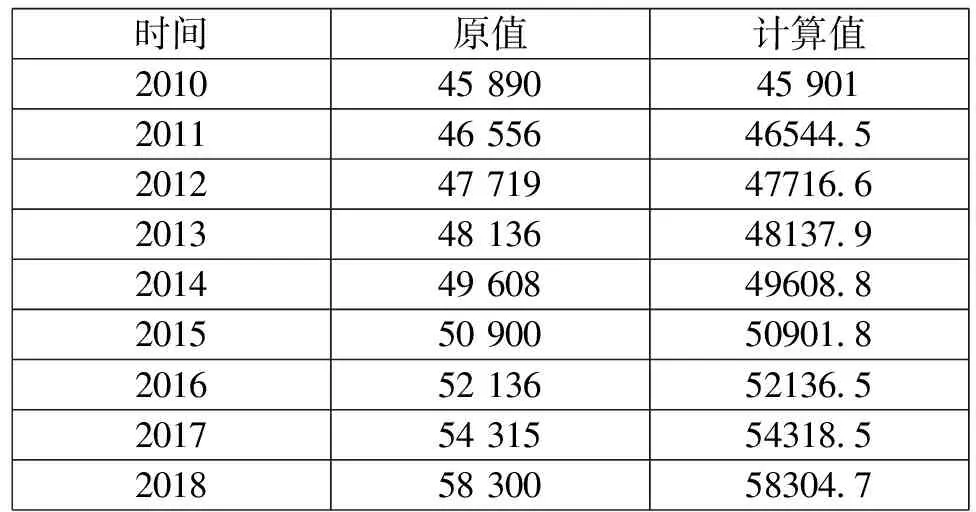
表3 基于BP神经网络建立的专业技术人才模型