在役钢筋混凝土渡槽多失效模式时变可靠度分析

常佳 祝彦知 纠永志 尚峰

摘 要：传统渡槽可靠度分析大多只考虑失效模式的单一性，为此，基于混凝土碳化模型与钢筋锈蚀模型提出了在役钢筋混凝土渡槽多失效模式的时变可靠度计算方法。利用Monte-Carlo法建立了单一失效模式的时变可靠度与失效概率计算方法，在单一失效模式的基础上采用PNET算法给出了多失效模式时变可靠度模型，运用Matlab软件编写了程序，对某在役钢筋混凝土渡槽结构在单一失效模式与多失效模式下的时变可靠度与失效概率进行了计算分析，结果表明：考虑多失效模式的渡槽可靠度小于单一失效模式的可靠度，计算结果更加合理；考虑渡槽多失效模式的时变性，能更好地掌握结构可靠度随时间的变化情况，给渡槽结构的耐久性做出合理的评价；采用多失效模式时变可靠度对渡槽的可靠度进行计算，与单一失效模式计算结果相比更符合渡槽实际。

关键词：在役钢筋混凝土渡槽；时变可靠度；多失效模式；PNET算法；Monte-Carlo法

中图分类号：TV331 文献标志码：A doi：10.3969/j.issn.1000-1379.2022.01.029

引用格式：常佳，祝彦知，纠永志，等.在役钢筋混凝土渡槽多失效模式时变可靠度分析[J].人民黄河，2022，44（1）：139-143，148.

Time VaryingReliabilityAnalysisofMulti FailureModesofReinforcedConcreteAqueductsinService

CHANGJia1，2，ZHUYanzhi1，2，JIUYongzhi1，2，SHANGFeng3（1.SchoolofCivilEngineeringandArchitecture，ZhongyuanUniversityofTechnology，Zhengzhou450007，China；2.ArchitecturalDesignandResearchInstitute，ZhongyuanUniversityofTechnology，Zhengzhou450007，China；3.DepartmentofCivilEngineering，ShanghaiUniversity，Shanghai200444，China）

Abstract：Traditionalreliabilityanalysisofaqueductsonlyconsidersthesingularityandtime invarianceoffailuremodes.Therefore，based onconcretecarbonationmodelandsteelcorrosionmodel，atime varyingreliabilitycalculationmethodformultiplefailuremodesofin service reinforcedconcreteaqueductswasproposed.Monte Carlomethodwasusedtocalculatethetime varyingreliabilityandfailureprobabilityofa singlefailuremode.Onthebasisofasinglefailuremode，atime varyingreliabilitymodelofmultiplefailuremodeswaspresentedbyusing PNETalgorithm.ThecorrespondingprogramwascompiledbyusingMatlabandthetime varyingreliabilityandfailureprobabilityofin servicereinforcedconcreteaqueductstructuresundersinglefailuremodeandmulti failuremodewerecalculatedandanalyzed.The calculationresultsshowthatthereliabilityvalueofaqueductconsideringmulti failuremodeislessthanthatofsinglefailuremodeandthe calculationresultsaremorereasonable.Consideringthetime varyingofmultiplefailuremodesofaqueduct，thevariationofaqueductstructur alreliabilitywithtimecanbebettergraspedandthedurabilityofaqueductstructurecanbereasonablyevaluated.Thereliabilityofaqueduct canbecalculatedbyusingtime varyingreliabilityofmultiplefailuremodes，whichismoreinlinewiththeactualsituationofaqueductcom paredwithsinglefailuremode.

Keywords：in servicereinforcedconcreteaqueduct；time varyingreliability；multiplefailuremodes；PNETalgorithm；Monte Carlomethod

渡槽結构在运行过程中受荷载水平与环境因素等多种不确定因素影响，多种不确定因素决定着渡槽具有多失效模式。复杂结构体系的多失效模式之间存在一定相关性[1]，因此渡槽多失效模式的分析相对复杂。现有针对渡槽的可靠性研究多采用单一失效模式[2-3]，对渡槽结构进行安全性评价并不能全面、合理地评估其可靠度水平。此外，掌握渡槽结构可靠度随时间的变化情况更有利于其耐久性评估与后期维护。因此综合考虑结构失效模式的多样性与可靠度的时变性对渡槽的安全评价具有重要意义。

目前，已有许多学者基于多失效模式对实际工程开展可靠度研究。李典庆等[4]考虑多失效模式的相关性对岩体边坡可靠度进行了分析；胡魏玲等[5]针对混凝土重力坝，考虑其多失效模式，分析了其时变可靠度；蒋水华等[6]基于子集模拟方法，给出了边坡系统多失效模式概率的计算方法；杨智勇等[7]提出了广义子集模拟样本加权法，考虑边坡失效的多种模式，对边坡工程进行了可靠度分析；唐铁羽等[8]考虑裂缝与保护层碳化两种失效模式对钢筋混凝土结构进行了耐久性分析，但其未考虑可靠度的时变性；LYUQing等[9]利用响应面法，考虑岩石隧道多种失效模式，对其进行了可靠度计算分析；SungEunCho[10]采用FORM法（多点一阶估计法）进行了多种失效模式的边坡可靠度计算；钟佩[11]基于多失效模式，利用响应面法与Monte-Carlo法建立了钢筋混凝土桥梁的时变可靠度计算模型，并结合有限元分析软件ANSYS进行了桥梁时变可靠度分析。

上述研究的多失效模式对渡槽结构的针对性不强，其失效模式不符合渡槽的实际情况[4，11]。现有针对渡槽的耐久性分析多采用单一失效模式[2-3]，没有综合考虑渡槽结构失效的多样性与时变性。因此，笔者考虑在役钢筋混凝土渡槽失效模式的多样性与可靠度的时变性，运用有限元软件MidasCivil建立三维渡槽模型，分析其受力情况，确定影响渡槽结构耐久性的基本因素，基于Monte-Carlo法建立各单一失效模式的时变可靠度计算模型，利用Matlab软件编写基于PNET法（概率网络估算法）的结构多失效模式的失效概率与可靠度计算程序，并结合工程实例进行计算与分析。

1 各失效模型的极限状态方程

1.1 钢筋混凝土碳化的极限状态方程

一般认为混凝土的碳化深度X与碳化系数α、时间t的关系为X=αt，混凝土的碳化除了与时间相关外，还与环境、材料以及力学物理性质等因素有关。混凝土的碳化会引起钢筋锈蚀，从而导致钢筋保护层产生裂缝。保护层完全碳化，致使钢筋表面钝化膜消失，这一现象被认为是结构功能丧失的表现[13]。目前，针对混凝土碳化的研究相对成熟，本文依据潘洪科[14]提出的混凝土碳化公式建立渡槽结构碳化的失效模型。潘洪科综合考虑时间、水灰比以及应力水平，通过相关试验和工程实例得出了混凝土碳化模型：

4 实例计算与分析

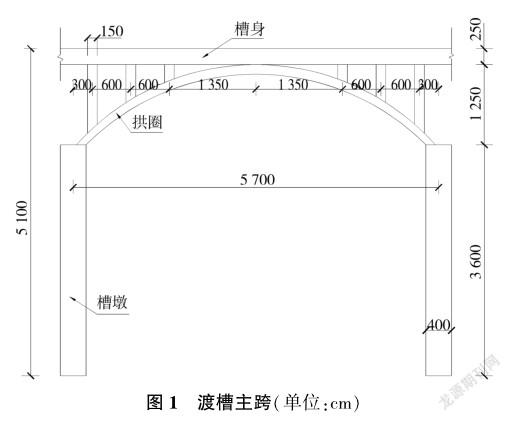
引沁灌区东方红渡槽位于河南省济源市，渡槽为上承式拱架钢筋混凝土结构，全长400m，高51m，设计流量为15m3/s，渡槽共有5个57m的主跨与1个25m的次跨，槽身为箱型结构，净高2.5m、净宽3.0m，渡槽主跨见图1。该渡槽1967年建成，至今已运行了50多a。2011年，即渡槽服役44a时对其进行了检测。经检测渡槽混凝土强度等级为C20，保护层厚度为35mm，钢筋直径为20mm。检测时发现渡槽存在一定数目的裂缝，裂缝宽为0.50～0.70mm，最大碳化深度为23.4mm，钢筋有一定程度的锈蚀。

4.1 有限元模型建立

为确定影响结构碳化与钢筋锈蚀的参数值，计算结构各部位的受力情况，将上部水流简化为均布荷载，利用有限元软件MidasCivil建立渡槽三维模型并进行渡槽结构受力计算。有限元模型输入参数重度、弹性模量、泊松比、内聚力、内摩擦角、强化参数分别为24.0kN/m3、25.5GPa、0.2、1000.0kPa、47.0°、411.0kPa，渡槽部分有限元模型见图2。经有限元分析，渡槽主墩多数区域轴向压应力为1.6MPa，拱圈轴向压应力为2.59～4.01MPa，多数区域轴向应力大于3MPa，槽身轴向应力为-0.63～0.63MPa，最大弯矩为2930kN·m，因此可以确定压应力σc的平均值为3.3MPa，变异系数取0.24。

4.2 失效模式参数确定

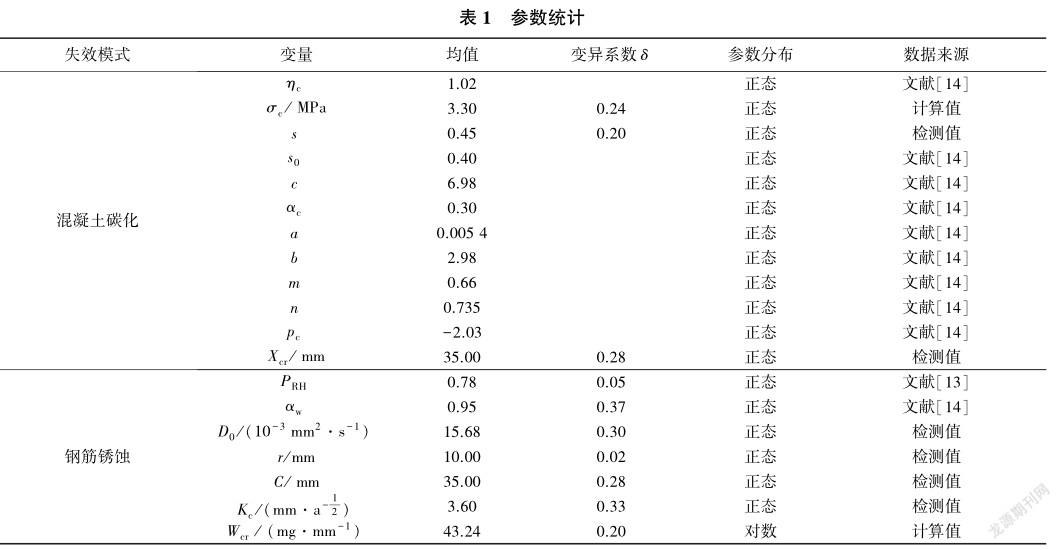
通过有限元模拟可以确定结构各部位的受力，此外影响渡槽结构耐久性的因素还有水灰比、混凝土强度、环境因素等，具体参数见表1。

4.3 渡槽时变可靠度计算与分析

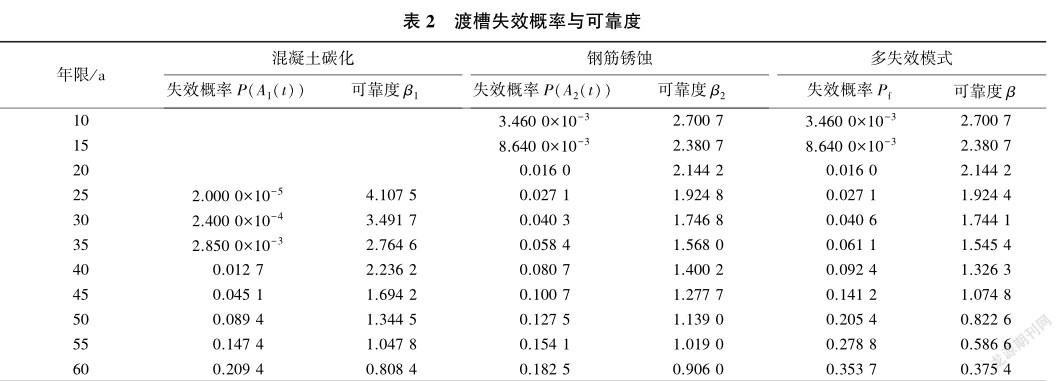
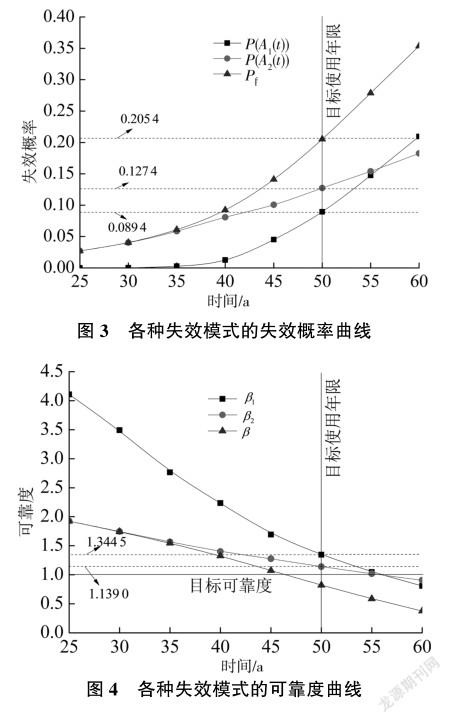
基于Monte-Carlo抽样法，利用Matlab软件编写了每种失效模式的时变可靠度与失效概率计算程序，根据PNET法编写了考虑多失效模式的结构时变可靠度与失效概率计算程序。根据表1数据利用Monte-Carlo法进行了10万次满足各变量概率分布的随机抽样，对上述两种失效模式进行计算，利用式（10）～式（14）分别计算钢筋混凝土渡槽因碳化而失效的时变可靠度β1与失效概率P（A1（t）），渡槽因钢筋锈蚀而失效的时变可靠度β2与失效概率P（A2（t）），考虑渡槽多失效模式的时变可靠度β与失效概率Pf，计算结果见表2、图3、图4。

从图3、图4可以看出，随着时间的增加，在任一种失效模式下结构的失效概率均不断增大，可靠度均不断下降；单一失效模式的结构失效概率比多失效模式的结构失效概率小；在多失效模式下结构的可靠度小于单一失效模式下结构的可靠度。一般建筑物目标使用年限为50a，最低目标可靠度為1.0[17]。2011年即渡槽服役44a时对渡槽进行检测发现，其存在多处因结构损伤而漏水的现象，还存在多处横向裂缝，说明此时渡槽已丧失正常使用功能，查看规范[17]可知其可靠度为1.0左右，由表2可知此时多失效模式时变可靠度计算结果为1.08左右，证明了本文可靠度计算模型的正确性。此外，对图4中3种不同失效模式进行对比可以看出，在到达目标使用年限时仅有多失效模式的渡槽可靠度值小于1.0，即考虑结构多失效模式的时变性可以很好地掌握渡槽结构可靠度的动态变化，便于渡槽的维修，更加合理。

5 结 论

为了更加合理地评估在役钢筋混凝土渡槽结构的时变可靠度，采用Monte-Carlo法建立了考虑多失效模式的渡槽时变可靠度计算模型，利用Matlab软件编写了基于PNET法的渡槽时变可靠度与失效概率计算程序，结合实际工程进行了计算与分析。通过计算分析可以得出以下结论：考虑渡槽多失效模式的失效概率要比考虑单一失效模式的失效概率大，其可靠度比单一失效模式的可靠度小，考虑多失效模式较单一失效模式的可靠度计算值更加合理；考虑渡槽多失效模式的时变性，能更好地掌握结构可靠度随时间的变化情况，给渡槽结构的耐久性做出合理评价；采用多失效模式时变可靠度对某渡槽的可靠度进行计算，结果表明该渡槽在运行45a时结构可靠度为1.0748，与单一失效模式计算结果相比更符合渡槽实际，若采用单一失效模式的可靠度或采用目标使用年限对渡槽结构进行检修将会偏于不安全。

参考文献：

[1] 鲁乃唯，刘扬.桥梁可靠度分析方法与应用[M].南京：东南大学出版社，2017：9-10.

[2] 祝彦知，尚峰，纠永志.在役钢筋混凝土渡槽时变模糊可靠度分析[J].水利水电技术，2019，50（2）：128-132.

[3] 席晓辉.基于响应面法的预应力渡槽结构可靠度研究[D].郑州：华北水利水电大学，2018：25-27.

[4] 李典庆，周创兵.考虑多失效模式相关的岩质边坡体系可靠度分析[J].岩石力学与工程学报，2009，28（3）：541-551.

[5] 胡魏玲，邓念武，刘任莉.基于多模式相关的混凝土重力坝服役寿命研究[J].中国农村水利水电，2016（6）：150-154.

[6] 蒋水华，刘贤，姚池，等.低概率水平岩质边坡系统可靠度分析[J].岩土力学，2018，39（8）：2991-3000.

[7] 杨智勇，李典庆，曹子君，等.基于广义子集模拟样本加权法的边坡多失效模式可靠度分析[J].岩石力学与工程学报，2018，37（3）：630-641.

[8] 唐铁羽，赵国藩.混凝土结构裂缝及保护层碳化极限状态可靠性[J].大连理工大学学报，1997，37（增刊1）：156-158.

[9] LYUQing，XIAOZhipeng，JIJian，etal.ReliabilityBased DesignOptimizationforaRockTunnelSupportSystemwith MultipleFailureModesUsingResponseSurfaceMethod[J]. TunnellingandUndergroundSpaceTechnologyIncorporating TrenchlessTechnologyResearch，2017，70：1-10.

[10] SUNGEunCho.First OrderReliabilityAnalysisofSlopeCon sideringMultipleFailureModes[J].EngineeringGeology，2013，154：98-105.

[11] 鐘佩.基于响应面法的预应力混凝土梁桥可靠度分析与寿命预测[D].武汉：武汉理工大学，2009：33-37.

[12] 赵国藩，曹居易，张宽权.工程结构可靠度[M].北京：科学出版社，2011：25-26.

[13] 牛荻涛.混凝土结构耐久性与寿命预测[M].北京：科学出版社，2003：34-36.

[14] 潘洪科.基于碳化作用的地下工程结构的耐久性与可靠度[D].上海：同济大学，2005：64-65.

[15] 牛荻涛，王庆霖，王林科.锈蚀开裂前混凝土中钢筋锈蚀量的预测模型[J].工业建筑，1996（4）：8-10，62.

[16] 康崇禄.蒙特卡罗方法理论和应用[M].北京：科学出版社，2014：127-131.

[17] 中华人民共和国住房和城乡建设部，国家市场监督管理总局.建筑结构可靠性设计统一标准：GB50068—2018[S].北京：中国建筑工业出版社，2018：12-13.

【责任编辑 吕艳梅】