基于雨型分析的小流域山洪灾害临界雨量计算

沈炜彬 郝鹏

摘 要：山洪灾害对人们的生命财产安全造成极大的危害。雨型是影响水文过程的重要因素，雨型的不确定性将影响临界雨量计算的准确性，给山洪灾害的预警预报带来很大的挑战。基于此，采用Copula函数，以雨型特征参数总雨量和峰值雨强为控制条件，提出了概率雨型设计方法，并通过HEC-HMS水文模型模拟降雨—径流过程，采用试算法计算多情景模式的临界雨量阈值空间。陕西罗敷堡小流域实例计算结果表明：概率雨型设计方法合理且简单实用；HEC-HMS模型对小流域山洪灾害具有较好的模拟效果；前期影响雨量和雨型对临界雨量均有影响，不同条件下二者影响程度不同。

关键词：山洪灾害；小流域；概率雨型；临界雨量；Copula函数

中图分类号：TV122 文献标志码：A doi：10.3969/j.issn.1000-1379.2022.01.011

引用格式：沈炜彬，郝鹏.基于雨型分析的小流域山洪灾害临界雨量计算[J].人民黄河，2022，44（1）：52-57.

CalculationofCriticalRainfallofFlashFloodinSmallWatershedBasedonRainfallPatternAnalysis

SHENWeibin1，HAOPeng2

（1.HangzhouCityPlanningConsultationCo.，Ltd.，Hangzhou310012，China；2.PressandPublicationCenter，YRCC，Zhengzhou450003，China）

Abstract：Flashfloodcausesgreatharmtopeople slifeandpropertysafety.Rainfallpatternisanimportantfactoraffectingthehydrological process.Theuncertaintyofrainfallpatternwillaffecttheaccuracyofcriticalrainfallcalculation，whichbringsgreatchallengestotheflash floodearlywarningandforecasting.Basedonthis，aprobabilisticrainfallpatterndesignmethodwasproposedbyusingtheCopulafunction andtakingthetotalrainfallandpeakrainfallintensityasthecontrolconditions，andtherainfall runoffprocesswassimulatedbytheHEC HMShydrologicalmodel.Atrialalgorithmwasusedtocalculatethecriticalrainfallthresholdspaceundermultiplescenarios.Takingasmall watershedinLuofubao，ShanxiProvinceasanexample，thecalculationresultsshowthattheprobabilityrainfallpatterndesignmethodisrea sonable，simpleandpractical.HEC HMSmodelhasagoodsimulationeffectforflashfloodinsmallwatershed.Boththeantecedentinfluence rainfallandtherainfallpatternhaveinfluenceonthecriticalrainfall，andtheinfluencedegreeisdifferentunderdifferentconditions.

Keywords：flashflood；smallwatershed；probabilisticrainfallpattern；criticalrainfall；Copulafunction

山洪灾害通常指因降雨而在山丘区引发的洪水灾害，对人类的生命和财产安全造成威胁，对自然环境、基础设施、公共环境等造成严重破坏[1-2]。根据多年统计，山洪灾害伤亡人数占洪涝灾害伤亡人数的70%左右[3]，山洪灾害已经成为中国洪涝灾害致人死亡的主要灾种。因此，做好山洪灾害预警预报工作对防灾减灾具有重要意义。

临界雨量是目前最常用的山洪灾害预警指标，其计算方法可分为数据驱动法和水文水力学法。由于水文水力學法中的水文模型能够考虑山洪灾害成灾物理机制，并能兼顾下垫面、气象环境等因素，因此得到广泛应用[4-5]。雨型作为水文模型的输入条件，是影响水文过程的重要因素[6-7]，目前的雨型研究多将研究重点放在雨量时程分配方面。岑国平等[8]模拟了4种雨型的暴雨径流过程，研究结果表明雨型对洪水过程有较大影响。侯精明等[9]通过模拟不同重现期和峰值比的暴雨致灾过程，揭示了降雨形态与洪灾程度的定量关系。Yuan等[10]基于设计降雨模式中不同雨峰位置提出了4种降雨模式来计算临界雨量。Park等[11]提出了3d降雨模式来更好地重现降雨事件的时程特征。以上研究虽然丰富了雨型的研究，但大多采用固定的降雨模式，忽略了降雨不确定性对临界雨量的影响。随着全球气候变化的加剧，突发性降雨事件的频率增大，雨型的不确定性增强，因此在临界雨量计算中必须考虑雨型的不确定性。

Hong等[12]认为准确的降雨量预测对于减少山洪暴发造成的损失至关重要；杨星等[13]研究表明可以用总降雨量和时段降雨量表征降雨事件；Palynchuk等[14]认为峰值雨强对降雨有较大影响。本文基于雨型的不确定性，选取总雨量和峰值雨强作为表征雨型不确定性的特征值，运用Coupla函数原理提出概率雨型的定义及设计方法，并通过HEC-HMS水文模型模拟计算研究区概率雨型多情景下临界雨量的阈值空间，揭示雨型不确定性与临界雨量的响应关系。

1 研究方法

1.1 概率雨型设计方法

1.1.1 概率雨型定义

1.1.2 分布函数优选

总雨量和峰值雨强的联合分布是计算风险组合概率的关键因素，若实际情况的分布与假设的分布不一致，则易导致风险概率出现较大偏差。确定单变量边缘分布的方法分为参数法和非参数法。对于总雨量和峰值雨强的联合分布，采用Copula函数进行确定。由于Copula函数要求随机变量之间具有相关关系，因此采用3种相关系数对总雨量和峰值雨强的相关性进行分析。在此基础上，选用3种二维Copula函数构造总雨量和峰值雨强联合分布，通过RMSE（RootMean SquareError）准则法、AIC（AkaikeInformation Criterions）信息准则法以及BIC（BayesianInformation Criterions）信息准则法对拟合优度进行评价，确定拟合度较优的Copula函数来构造联合分布函数。构造的总雨量和峰值雨强联合分布函数可用式（3）表示。

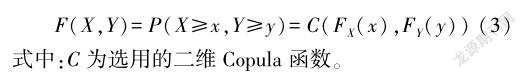
1.1.3 雨量时程分配

推求风险组合概率雨型的核心部分为该雨型综合雨峰时段峰值雨强和其他时段雨量的确定。在降雨总时段数为n、雨峰与实际降雨资料中雨峰出现频次最高时段tm一致的场次降雨集合ω中，计算除雨峰时段外的各时段降雨量百分比均值d-i及其占百分比均值之和的比例xi（m为雨峰出现频次最高时段编号，i为除雨峰时段外的各时段编号）：

1.2 临界雨量计算

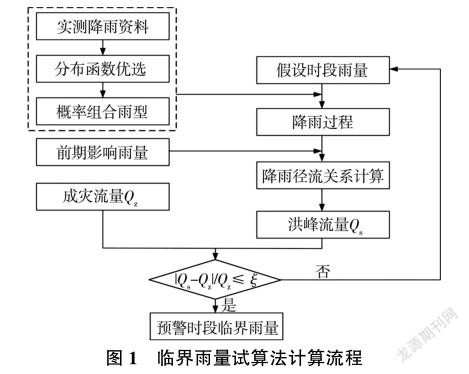
试算法因其结果准确、精度较高而被应用于山洪灾害临界雨量计算中。通过假定初始时段雨量，采用上述概率雨型进行降雨时程分配。将得到的降雨过程输入水文模型进行降雨—径流关系计算，得到洪峰流量，将其与成灾流量对比，若二者相对误差满足精度要求，则假设的雨量即相应预警时段的临界雨量；若不满足精度要求，则重新假设初始时段雨量，反复试算，直至满足精度为止。基于概率雨型的山洪灾害临界雨量试算法具体过程如图1所示（图中ξ表示允许误差）。

1.3 降雨—径流关系计算

考虑降雨—径流关系的灵活性和适用性，采用HEC-HMS模型模拟小流域的降雨—径流过程[15]。该模型包括流域模块、气象模块、控制模块和时间序列模块，其中流域模块由降雨损失、直接径流、基流和河道汇流四部分组成。每次降雨—径流过程模拟都会调用上述4个模块。模型结构和模块调用的详细信息可参考HEC-HMS技术参考手册[16]。HEC-HMS模型可根据实测资料和流域条件选择合适的方法组合来计算降雨径流关系，然后利用研究区实测数据对HEC-HMS模型的参数进行校正，通过对洪水实测值与模拟值的比较，确定最佳的模拟参数。合适的方法组合选择过程和参数校准过程可参考文献[17-18]。

2 实例分析

2.1 研究区概况

选取陕西省华阴市罗敷堡小流域为研究区域，选取该小流域中源头村二组为典型防灾对象。罗敷堡小流域位于华阴市西部，流域面积为132km2，流域内最长汇流路径为23.89km，河道平均比降为0.0498，属于典型的山丘区小流域。该小流域地势落差较大，土地植被覆盖率高，易较快产生地表径流而暴发山洪灾害，故选择该小流域作为典型小流域进行研究。研究区域如图2所示。

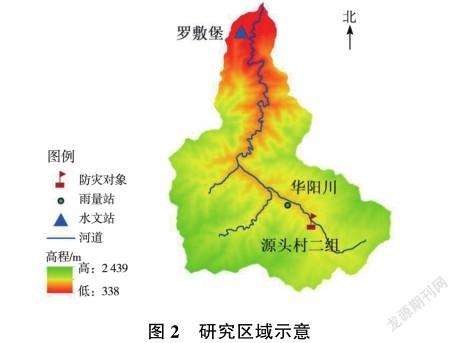
2.2 数据来源

本文使用的数据包括GIS数据、降雨数据和洪水数据，其中GIS数据来自中国国家地理信息中心，包括数字高程数据（DEM）、土壤类型数据和土地利用类型数据等。实测降雨资料采用华阳川雨量站1980—2018年资料，实测洪水资料采用罗敷堡水文站1982—2018年资料，时间分辨率取1h。经过统计分析，总历时为12h的降雨场次占比最高，共计44场次，因此本文提出的概率雨型确定方法采用总历时为12h的降雨資料。

2.3 Copula函数优选

P-Ⅲ分布是水文频率分析计算常用的方法之一，本文采用P-Ⅲ分布对总雨量进行拟合。非参数法不依赖总体分布，应用范围广，故峰值雨强的分布通过非参数核密度估计法确定。通过K-S检验验证所选边际分布函数的合理性，并通过Pearson线性相关系数r、Kendall秩相关系数τ和Spearman秩相关系数ρ分析总雨量与峰值雨强的相关性，结果见表1、表2。总雨量和峰值雨强的边缘分布均小于临界值，这表明假设的边缘分布合理。总雨量和峰值雨强边缘分布的三种相关系数均大于0.8，说明二者有较好的相关性，符合构建Copula函数的条件。

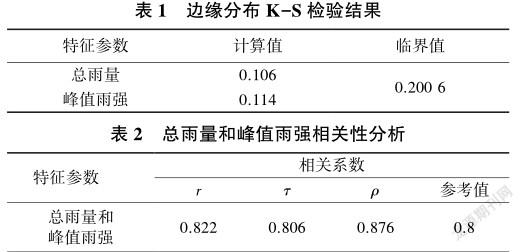
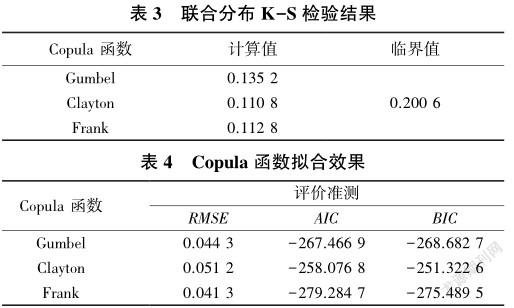
采用Gumbel、Clayton和Frank三种Copula函数来优选最优的联合分布函数，其中K-S检验结果和拟合效果见表3和表4。由表3可知，所有K-S检验结果（经验累积概率与目标理论累积概率之差的最大值）均小于临界值，说明Gumbel、Clayton和Frank均可用来建立总雨量和峰值雨强的联合分布。从表4可以看出，在3种拟合优度评价标准中，Frank函数的所有评价值均最小，说明Frank函数的拟合优度最好，因此选择Frank函数作为联合分布函数。

2.4 水文模型應用评估

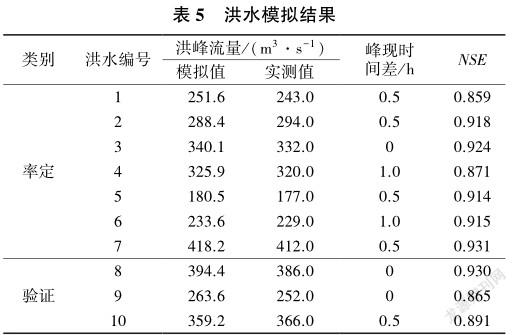
根据上述降雨—径流关系模拟方法，选用罗敷堡水文站10场洪水资料进行模拟，其中7场洪水用于HEC-HMS模型参数率定，3场洪水用于验证。模拟结果见表5，洪峰流量的模拟值与实测值的相对偏差均小于10%，且峰现时间差最大不超过1h。此外，经常被用来评估水文模型有效性的Nash-Sutcliffe效率系数（NSE）均大于0.8。以上结果表明计算模型合理可靠，HEC-HMS模型可以有效地应用于该流域。

2.5 概率雨型合理性分析

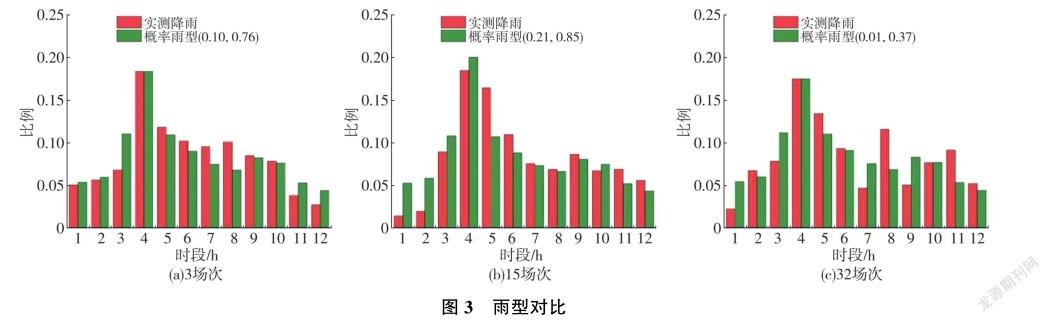
从实测降雨资料中选择3场降雨资料进行概率雨型合理性分析，通过确定3场实测降雨的总雨量和峰值雨强进而确定相应的概率，然后根据式（4）～式（7）计算相应的概率雨型，计算结果见图3。可以看出3种概率雨型的峰值位置与实测降雨相同，且峰值强度相差不大。此外，每场概率雨型均有一个单一的峰值，且雨峰位置靠前，与实测降雨雨峰位置相同。概率雨型具有与实测降雨保持趋势一致的特性。

在上述雨型对比分析的基础上，按照式（8）计算概率雨型与实测雨型的贴合度，并按照式（9）计算基于概率雨型的临界雨量与时段特征雨量偏离度，计算结果见表6和表7。

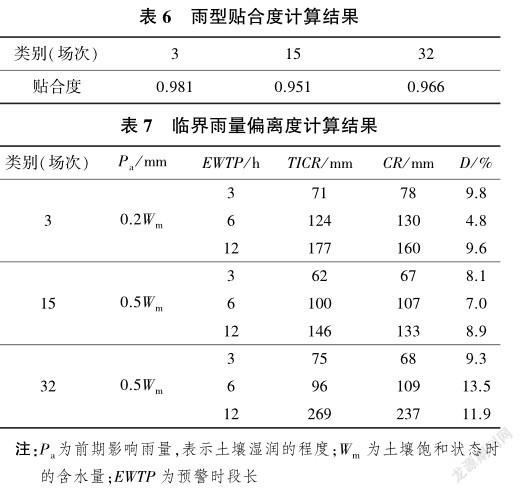
可以看出，3种概率雨型与实测降雨的贴合度均大于0.95，表明概率雨型与实测降雨过程较为吻合。3场实测降雨的各个预警时段的临界雨量和时段特征雨量偏离度均小于15%，满足精度要求，即基于概率雨型的临界雨量具有较高的可靠性。雨型贴合度和临界雨量偏离度计算结果表明本文提出的概率雨型是合理的，可以用于山洪灾害临界雨量计算。

2.6 概率雨型对临界雨量的影响

综合考虑源头村二组防灾能力，研究区前期影响雨量以及雨型不确定性，设置（0.02，B）、（0.05，B）、（0.10，B）三种雨型集合来探究概率雨型对临界雨量的影响，概率雨型和临界雨量计算结果分别见图4和图5。

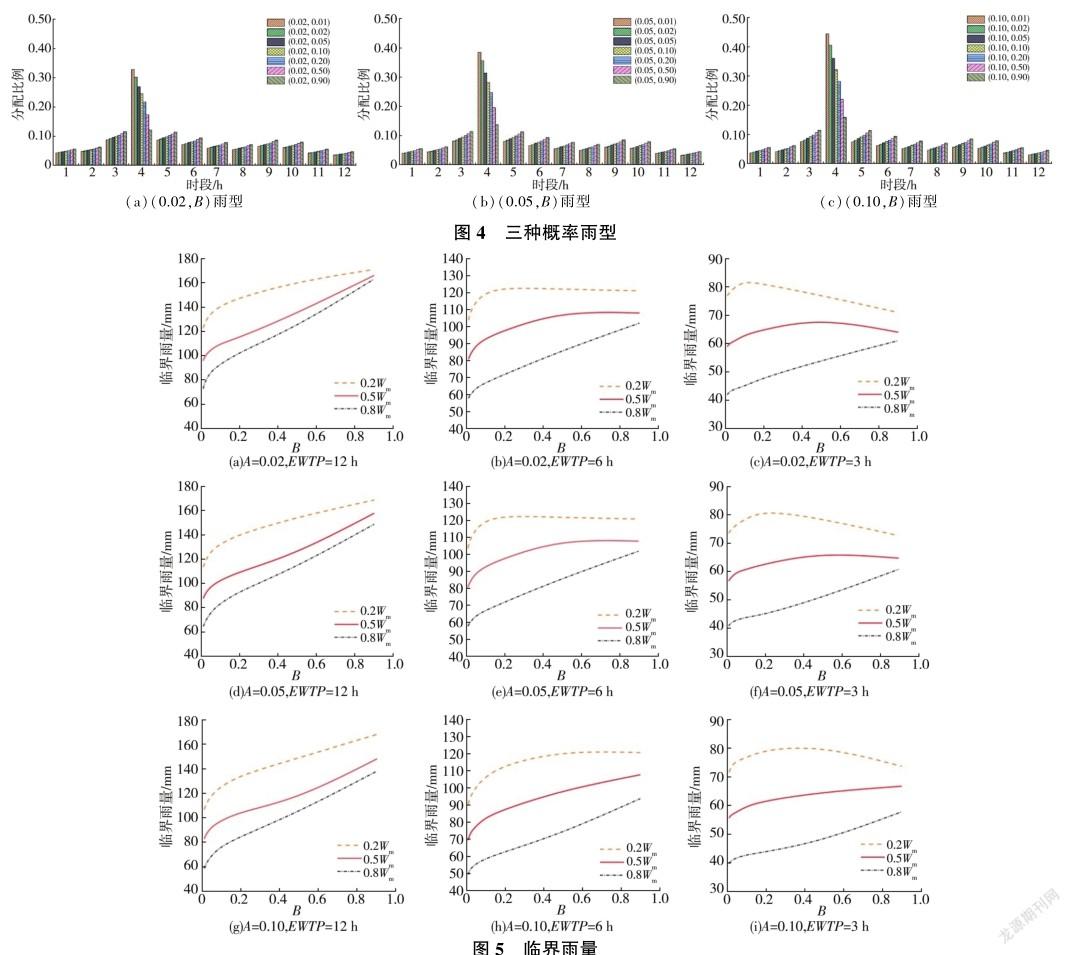
由图5可知，前期雨量越小，临界雨量越大。12、6、3h的临界雨量阈值分别为37～163、53～101、41～61mm，对应的临界雨量变化范围分别为90、48、20mm，这些变化表明雨型对降雨强度的影响很大。当总雨量概率一定时，源头村二组不同前期影响雨量的临界雨量曲线随着峰值雨强概率的增大而逐渐靠近，其原因是峰值雨强的概率越大，峰值雨强数值越小，雨峰在雨量时间分布中的作用减弱，雨型均匀性增强，如图4所示。均匀降雨可以充分发挥流域的调蓄功能，减少前期影响雨量对临界雨量的影响。3种预警时段中，12h的临界雨量曲线最集中，3h的临界雨量曲线最分散，该结果表明调蓄时间越长，前期影响雨量对临界雨量的影响越小。

3 结 论

本文基于研究区域实际降雨资料及灾害信息，针对雨型不确定性问题，利用Copula函数理论建立基于总雨量和峰值雨强的概率雨型，对多情景风险组合概率雨型临界雨量的阈值空间进行研究，结论如下。

（1）基于Copula函数的概率雨型设计方法简单实用，概率雨型能够较好地反映真实的降雨过程。

（2）HEC-HMS模型模拟的流域洪峰与实测洪峰非常接近，证明降雨—径流过程的模拟结果是合理和可靠的，HEC-HMS模型对山丘区小流域山洪暴发具有较好的模拟效果。

（3）前期影响雨量和雨型都对临界雨量有影响，但在总雨量一定的情况下，峰值雨强的减小会减弱前期影响雨量对临界雨量的影响。此外，降雨持续时间的延长也会减弱前期影响雨量对临界雨量的影响。

本文提出的概率雨型设计方法仅适用于单峰型降雨计算，不能覆盖研究区所有可能的雨型。在后续的研究中应注意多峰型雨型的不确定性，从而确定准确的临界雨量，进一步提高山洪预警的准确性。

参考文献：

[1] HAPUARACHCHIHAP，WANGQJ，PAGANOTC.AReview ofAdvancesinFlashFloodForecasting[J].Hydrological Processes，2011，25：2771-2784.

[2] 高倩雨.基于Copula函数的小流域山洪灾害风险组合概率临界雨量研究[D].郑州：郑州大学，2019：12-35.

[3] 何秉顺，黄先龙，郭良.我国山洪灾害防治路线与核心建设内容[J].中国防汛抗旱，2012，22（5）：19-22.

[4] 原文林，宋汉振，刘美琪.基于随机雨型的山洪灾害预警模式[J].水科学进展，2019，30（4）：515-527.

[5] ADAMOVICM，BRANGERF，BRAUDI，etal.Development ofaData DrivenSemi DistributedHydrologicalModelfor RegionalScaleCatchmentsPronetoMediterraneanFlash Floods[J].JournalofHydrology，2016，541：173-189.

[6] DIEDEREND，LIUY.DynamicSpatio TemporalGenerationof Large ScaleSyntheticGriddedPrecipitation：withImproved SpatialCoherenceofExtremes[J].StochasticEnvironmental ResearchandRiskAssessment，2020，34（9）：1369-1383.

[7] YUANWL，LIUMQ，WANF.StudyontheImpactofRainfall PatterninSmallWatershedsonRainfallWarningIndexofFlash FloodEvent[J].NaturalHazards，2019，97（2）：665-682.

[8] 岑国平，沈晋，范荣生.城市设计暴雨雨型研究[J].水科学进展，1998，9（1）：42-47.

[9] 侯精明，郭凯华，王志力，等.设计暴雨雨型对城市内涝影响数值模拟[J].水科学进展，2017，28（6）：820-828.

[10] YUANWL，LIUMQ，WANF.CalculationofCriticalRainfall forSmall WatershedFlashFloodsBasedontheHEC HMS HydrologicalModel[J].WaterResourcesManagement，2019，33（7）：2555-2575.

[11] PARKH，CHUNGG.ANonparametricStochasticApproachfor DisaggregationofDailytoHourlyRainfallUsing3 Day RainfallPatterns[J].Water，2020，12（8）：2306.

[12] HONGWC，PAIPF.PotentialAssessmentoftheSupport VectorRegressionTechniqueinRainfallForecasting[J]. WaterResourcesManagement，2007，21（2）：495-513.

[13] 杨星，朱大栋，李朝方，等.按风险率模型分析的设计雨型[J].水利学报，2013，44（5）：542-548.

[14] PALYNCHUKBA，GUOYP.AProbabilisticDescription ofRainStormsIncorporatingPeakIntensities[J].Journalof Hydrology，2011，409（1-2）：71-80.

[15] 原文林，付磊，高倩雨.基于HEC-HMS模型的山洪灾害临界雨量研究[J].人民黄河，2019，41（8）：22-27，31.

[16] USACE HEC.HydrologicModelingSystemHEC HMSTechnical ReferenceManual[R].Davis：USArmyCorpsofEngineers，HydrologicEngineeringCentre（HEC），2000：16-28.

[17] DUJK，QIANL，RUIHY，etal.AssessingtheEffectsofUr banizationonAnnualRunoffandFloodEventsUsinganIn tegratedHydrologicalModelingSystemforQinhuaiRiverBa sin，China[J].JournalofHydrology，2012，464：127-139.

[18] ZELELEWDG，LANGONS.SelectionofAppropriateLoss MethodsinHEC HMSModelandDeterminationoftheDe rivedValuesoftheSensitiveParametersforUn Gauged CatchmentsinNorthernEthiopia[J].InternationalJournal ofRiverBasinManagement，2020，18（1）：127-135.

【責任编辑 许立新】