威宁边界层风廓线雷达与探空系统的风向风速一致性初探

杨 哲，李 源，张玉逵，陈银东

(1.贵州省大气探测技术与保障中心，贵州 贵阳 550081；2.贵州省人工影响天气办公室，贵州 贵阳 550081；3.贵州省气象服务中心，贵州 贵阳 550002；4.贵州省威宁彝族回族苗族自治县气象局，贵州 威宁 553100)

0 引言

风廓线雷达自20世纪70年代末诞生以来，在很多国家的气象服务行业得到广泛应用，美国、日本、英国、德国等发达国家已经建成风廓线雷达网。我国于1989年研制出自己的风廓线探测系统，经过多年发展，已成功研制了平流层、对流层和边界层等多种探测高度的风廓线雷达。2019年贵州省气象部门在毕节威宁和安顺普定分别布设了2部边界层风廓线雷达。该雷达对晴空湍流、辐合辐散、急流区、切变线等天气系统有较快较好的辨别力，可为降水过程尤其是强对流天气的探测识别、预测预警提供重要参考。为确保该雷达数据可有效应用于贵州的气象预报预警和天气系统分析，本文对其在贵州复杂山地气候环境中探测数据的可靠性预先进行验证分析。目前国内外专家在风廓线探测数据的分析质控和应用等方面取得了一定成果，周志敏等[1]利用加密探空资料对咸宁市黑山观测站的风廓线数据进行了初步验证，发现其可靠性较好。王欣等[2]对风廓线资料与同步探空资料进行对比，分析了风廓线资料的可信度。万蓉等[3]设定风廓线雷达和加密探空资料风速差<3 m·s-1或风向差<20°为有效样本，并从降水情况、速度、高度条件的影响下进行分析研究。张寅等[4]利用探空数据、ERA再分析资料和同期风廓线雷达数据进行对比分析，表明该雷达在平均态过程中与探空和再分析资料基本一致。黄金权等[5]利用风廓线雷达产品对强对流天气过程进行应用分析。WEBER等[6]国外学者对比分析了风廓线雷达与常规探空的风场资料，结果显示：二者水平风速的u、v分量标准差为2.5 m·s-1。贵州省威宁县气象局观测站内同时布设有风廓线雷达和探空系统，并已具有较长时间的观测资料，为2种设备的数据对比分析[7]提供了一定基础。

1 资料选取及处理

CFL-03型边界层风廓线雷达和L波段探空雷达均位于贵州威宁县气象局内，两者海拔高度相差2 m左右，水平距离50 m左右。由于受边界层风廓线雷达性能和本地天气特征影响[8]，其可靠探测范围是以雷达为中心，平面半径约3 km、垂直高度3.5 km以下的空间。探空气球随风场扰动运动，探空气球从地面释放至3.5 km高度处，距离本站的水平距离存在3～20 km的偏差，剔除偏差>15 km的数据，可近似认为2部设备探测空间一致性满足要求。

探空气球释放具体时间为07时15分左右和19时15分左右，上升至3.5 km处需约9 min，故在0～3.5 km对比空间内探空气球探测时间为07时15—24分和19时15—24分。风廓线雷达每6 min出1组数据，选取07时24分和19时24分出的数据可使两者时间偏差最小，可视为满足时间一致性要求。

本研究使用的风廓线雷达产品为实时风场数据，该数据已指定各高度层风场信息。探空雷达则使用基础探空数据，该数据每秒钟回传1组风速、风向、气压等气象要素信息，其高度区间是连续性的，故需要提取探空指定高度风速风向使其与风廓线雷达高度层一致。

2 数据分析对比

2.1 相关性分析

2.1.1 总体相关性分析 选取2019年6—12月威宁探空雷达的风向、风速数据和相应时间的风廓线雷达数据，分别计算6个月的风廓线雷达各高度的风速、风向平均值和探空对应高度的风速、风向平均值，并绘图2部设备的风速、风向平均值随高度变化曲线及其风速、风向差值曲线(图1)。

图1 2019年6—12月风廓线雷达和探空风向、风速平均值及其差值随高度变化曲线

对风廓线雷达和探空风向、风速平均值进行相关性分析，并利用统计学方法计算两者平均值差值的统计特性值，具体结果如表1。

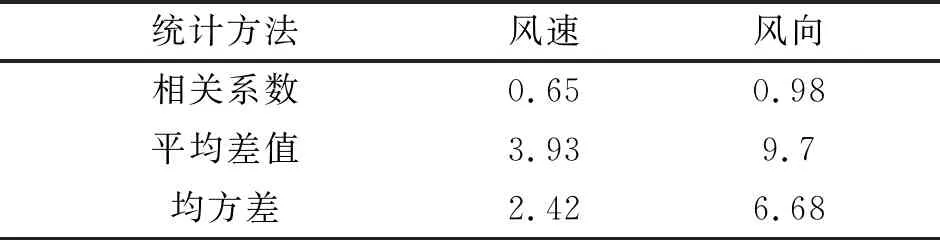
表1 风廓线雷达和探空风向、风速平均值的统计特征

根据图1和表1，风廓线雷达与探空的风向、风速平均值均具有一定正相关性，其中二者风向均值为高度相关，风速均值为中度相关。风速平均值的差值在高度为1000 m左右以下和3000 m左右高度以上均较大(>4 m·s-1)，1000～3000 m高度差值较小(<2 m·s-1)。风向平均值的差值在1000 m左右高度以下变化较大，最大约26°，1000 m以上差值趋于稳定总体在10°左右。

2.1.2 各次相关性统计 共收集整理风廓线和探空风速、风向数据序列(经规划化处理的单次探测数据文件)共4组总数为1596个，其中每个数据序列分别有399个，每个序列对应1次风速或风向随高度变化的实际探测数据。由于受探测环境和气象条件等因素影响，风廓线雷达和探空系统探测风场时在某些高度层不可避免会出现空值，经筛选统计，所选数据序列约10～40个左右数据值。将探空和风廓线雷达的风向、风速序列数据分别进行相关性分析，结果如图2所示。

图2 风廓线雷达和探空系统风向、风速相关系数统计

统计结果显示，满足显著性水平低于0.05的风速、风向个数分别为333、323，其中满足高度相关(相关系数≥0.8)的风速风向数据量分别为165、135，占比分别为49.6%、41.8%。满足中度相关(相关系数≥0.5)的风速风向数据量分别为278、275，占比分别为83.5%、85.1%。表明风廓线雷达和探空的风速风向数据具有较好的正相关性。

2.2 数据有效性分析

根据夏文梅等[9]研究结果，可以设定风廓线雷达与探空风速绝对差值在3 m·s-1以内，风向绝对差值在20°以内为有效样本。对风速、风向有效样本比率随高度变化进行统计并绘图，见图3。

统计得出风速有效样本占总样本比例为79.17%，风向有效样本占总样本比例为64.64%。当风向和风速的有效样本比>60%时，风廓线和探空资料就能达到相对较好的一致性，比率越大，一致性越好。根据图3可以看出，风速、风向有效样本比率在700 m以上高度主要维持在80%左右，表明除近地面外，风廓线雷达和探空风场数据总体一致性较好；在高度700 m左右以下由于地物干扰的存在，风速、风向有效样本比率较低；高度在1500～5000 m范围内有效样本比率变化幅度较小，表明该高度区间内风速、风向总体较其他高度更可靠；风速有效样本比率变化较风向的比率更均匀稳定。

图3 风向、风速有效样本比率随高度变化曲线(红虚线为0.6)

2.2.1 不同时次对比 采用08时、20时风廓线雷达和探空风场数据，统计出08时风向平均有效样本比率64.36%，风速平均有效样本比率78.01%；20时风向平均有效样本比率65.73%，风速平均有效样本比率73.56%。

如图4所示，在设定标准下根据统计结果，风速随高度变化的有效样本比率明显高于风向有效样本比率。08时和20时的风向平均有效样本比率均略低于风速样本比率，且风速风向有效样本比率随高度变化趋势相似。在2个时刻下500 m左右高度以下风速风向有效样本比率均大幅低于其他高度比率。表明风廓线雷达与探空系统的风速风向有效比率几乎不受08时和20时2个不同时刻的影响。

图4 北京时间08时、20时风速、风向有效样本比率随高度变化

2.2.2 不同降水情况对比 通过筛选分类出有降水和无降水的风廓线雷达和探空风场数据，然后分别计算出2种天气情况下风速风向有效样本在不同高度上的比率(图5)。有降水风速、风向平均有效样本比率分别为60.36%、55.49%，无降水风速、风向平均有效样本比率分别为80.12%、67.53%。

如图5所示，在有降水时，风廓线雷达与探空系统的风速、风向有效样本比率随高度变化的值均比无降水时较小一些，而且有降水时有效样本比率的变化幅度也相对较大；风向有效样本比率在有降水和无降水2种情况下均比风速有效样本比率较低。无论有无降水，风速风向有效样本比率在500 m左右高度以下均较低；有降水时的风速风向有效样本比率在4000 m以上高度也会变小。

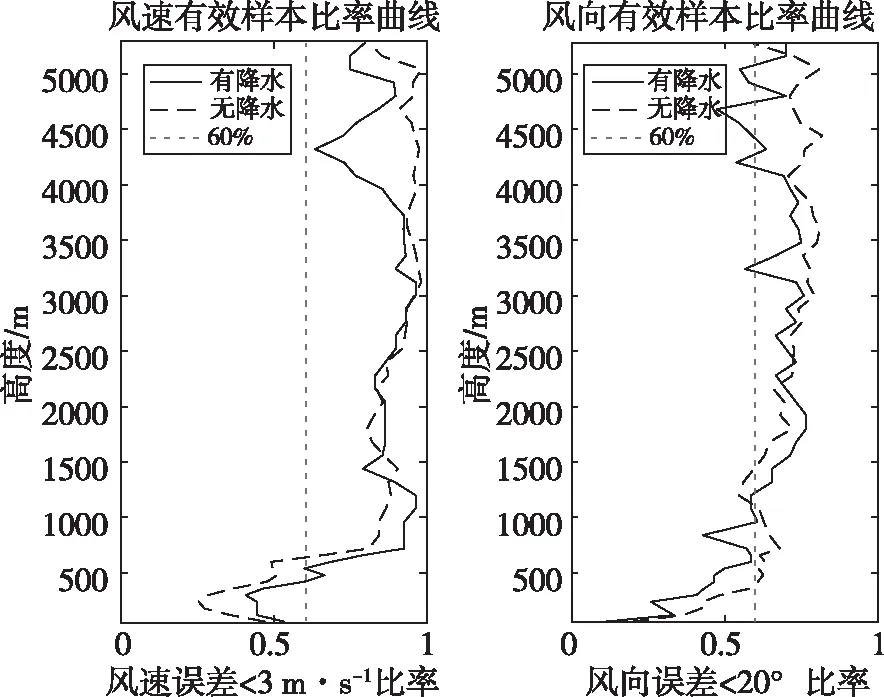
图5 有降水和无降水风速、风向有效样本比率随高度变化

2.2.3 不同风向对比 将风向分成18个方位范围，平均每个方位宽度为20°，再针对各个风向范围分别统计出风廓线和探空风向误差小于20°的有效样本比率，结果如图6所示。

由图6可以看出，西南方向的风向有效样本比率接近80%，东北方向有效比率接近70%，二者有效比率明显大于其他方向；即当风向为东北或西南时，风廓线雷达和探空的风向一致性好于其他方向。一致性最差的为东南风向，其风向有效样本比率不足40%，其次为正北和正东方向约40%左右。综合各个方向，满足一致性(有效样本比率≥60%)的方位合计为80°，不满足一致性的方位合计为280°，表明预设标准下方位有效性较差。

图6 风向有效样本比率随不同风向的变化

2.2.4 不同风速对比 将风速以3 m·s-1为一档共分为9档(如图7横轴所示)，再对风廓线雷达和探空分别在9个不同速度区间内的风速值进行统计。

图7 风速有效样本比率随风速大小的变化

如图7，风速有效样本比率随着风速增大而减小，风速<3 m·s-1时有效样本比率可达90%以上，风速>24 m·s-1时有效样本比率为不足40%的最小值，风速值处于3 m·s-1和24 m·s-1之间时风速有效样本比率均能达到60%以上，因此预设标准下，大部分风速区间均能满足一致性要求。

3 结果综述

本文从多个角度对威宁县风廓线雷达和探空系统的风速、风向数据相关性和有效性进行全面分析，预设2种气象设备探测到的风速差≤3 m·s-1、风向差≤20°为有效的数据样本，具体分析结果如下：

①从数据相关性角度来看，风廓线雷达与探空的风向总体上具有一定的正向高度相关性，风速具有一定的正向中度相关性；而在单次对比结果上，风速风向数据正向相关性较好，其中风速、风向满足中度相关的数据个数分别占总数据量的83.5%、85.1%。综合以上结果，风廓线雷达和探空系统的风速、风向数据具有较好的正向相关性。

②从数据有效性角度来看，根据预设标准，风速随高度变化的有效样本比率总高于风向有效样本比率，且无论有无降水或任意时次。在不同高度下，风速、风向数据样本有效比率总表现为低层(500 m左右高度以下)最小，最高层次之，中高层较大(最大可达90%)；在不同时次下，风向平均有效样本比率与风速样本比率随高度变化的值近似相等且其变化趋势相似；在不同降水情况下，风速、风向有效样本比率随高度变化的值在有降水时比无降水时总体偏小且变化幅度较大；在不同风向下，由于误差标准限定，除了东北和西南方位总计80°的方位区间外，2部设备的风向一致性在大部分方向上均较差；在不同风速下，除了24 m·s-1以上的风速外基本上都具有较好的一致性。

4 讨论分析

①由于风廓线雷达仅探测本站上空风场，而探空气球是随着风场扰动在运动，遇到风场条件较为复杂时，探空气球会出现忽近忽远或者远离测站上空的情况，难免会导致探测范围不一致。如果本站上空是受较为稳定的系统性流场控制，即使探空气球随气流飘到较远的地方，其所测到的风场与本站的风场也会相差较小。反之，若本站受局地性强对流控制，尤其是对流中存在风场切变、涡旋、辐合辐散等系统，风场小范围的变化会引起较大的风速风向差，影响风场数据的一致性。后续研究可以先对探测数据样本进行稳定性气流和局地性强对流等系统分类，然后再进行统计分析。

②根据研究结论可知，500 m左右高度是影响数据一致性的“拐点”，具体表现为在不同时次、不同降水条件下，500 m高度以下风速风向有效样本比率极低，而500 m以上风向风速有效样本比率相对会高很多。这是由于测站附近存在较多房屋、树木等地物，对风廓线雷达低层风场的探测产生了一定的干扰，使得雷达基数据受到污染，最终导致雷达探测获取到的风场数据可靠性降低。

③预设风速风向误差标准可以直接影响2个设备之间风速风向的有效样本比率，故选择合适又受认可的误差标准尤为重要。后续可以根据本地探测数据特征，利用大量的本地数据样本进行分析验证得到1个符合本地风场数据样本分析的误差标准。