“充填体-煤柱”复合结构势能突变破坏机理
王烁康,闫晶晶,阳元中
(1.河北石油职业技术大学数理部,河北承德 067000;2.中国矿业大学矿业工程学院,江苏徐州 221116)
煤炭是我国的主体能源,预计到2050 年煤炭占一次能源消费的比重仍在50%以上[1-2]。传统的粗放式开采易造成岩层运移、地下水资源流失、地表植被枯萎等生态问题[3]。充填开采能够有效控制岩层移动,是解决煤炭资源开采与生态环境保护之间矛盾的重要途径[4-5]。开采过程中,充填体逐步置换煤柱,覆岩的支撑结构由煤体变为“充填体-煤柱”复合结构(以下简称复合结构)。该结构的稳定承载既是煤炭安全开采的重要保障,又是实现煤炭绿色开采的前提。国内外学者对煤柱与充填体的稳定性问题进行了诸多理论研究与实践探索[6-10],学者们通常将煤柱或充填体视为柱体,顶、底板对柱体施加夹持作用开展相关研究。对于区段式,学者们得出了较为成熟的塑性区计算方法,例如A H 威尔逊两区约束理论、Kastner 公式等[11-12];对于条带式或块段式,学者们将直接顶(或基本顶)简化为板状结构,在载荷的作用下对煤柱或充填体做功,从系统能量突变的角度分析煤柱或充填体的稳定性[13-16];对于不规则柱体,如边角煤柱等,通过Voronoi 图的方法确定出有效承载面积,从而给出不规则煤柱稳定性评价标准[17-19]。前人成果多集中于单一承载结构稳定性的研究,且煤柱稳定性的判别多以强度理论与经验公式为主,与工程现场存在一定偏差。为此,以复合结构作为研究对象,将覆岩、煤柱与充填体系统相互作用力学模型与突变失稳数学模型相结合,揭示复合结构突变失稳的能量转化机制,为煤炭资源安全开采提供理论依据。
1 “充填体-煤柱”复合结构承载特征
1.1 力学模型
复合结构承受了自身上方全部覆岩质量,以及开采与充填空间上方部分覆岩质量。为建立复合结构力学模型,做出如下假设:
1)充填开采能够有效控制顶板,顶板下沉量相对采高是极小量,可忽略因充填先后顺序造成顶板下沉量的差异。
2)充填材料能够充满整个采空区,凝固后形成的充填体与覆岩、煤柱始终保持相互作用关系。
3)整个采空区范围内充填材料力学特性相同,且煤柱与充填体均具备连续性、均匀性以及各项同性等性质。
4)充填体与煤柱之间通过相互作用可形成复合承载结构,二者之间的区别仅限于物理力学参数的的不同。
5)覆岩载荷均匀分布于煤柱与充填体上方,复合结构变形特征可简化为平面应变问题。
基于巷式充填开采特征,建立的复合结构矿压和力学模型如图1 和图2。图中,M 为采高,m;L 为采场巷道宽度,m;a 为充填体宽度,m;b 为煤柱宽度,m;H 为煤层埋深,m;H1为采场巷道直接顶承载的覆岩高度,m;n 为复合结构与采场巷道的宽度之比;Y1、Y2分别为充填体与煤柱的塑性区宽度,m。
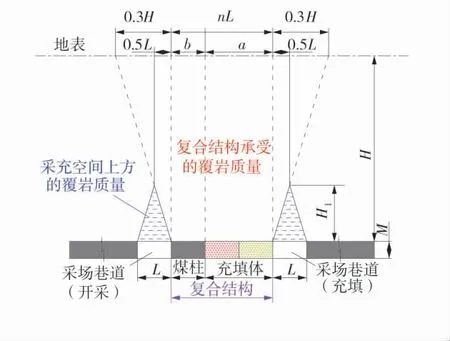
图1 复合结构矿压模型Fig.1 The rock pressure model of composite structure
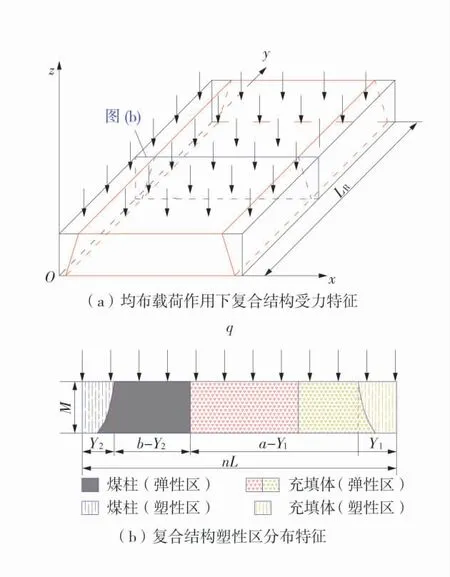
图2 复合结构力学模型Fig.2 The mechanical model of composite structure
复合结构承受的支承压力p 为:
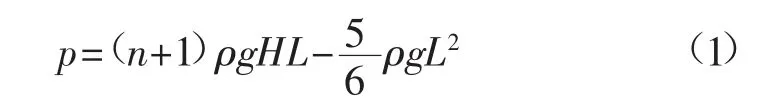
式中:ρ 为覆岩平均密度,取值2.5 t/m3。
1.2 复合结构总势能
复合结构承载过程中,会产生塑性区而降低有效支撑面积,当有效支撑面积减小到承载极限时将发生破坏失稳。复合结构弹性核区与塑性区的本构关系不同,前者呈线性关系,而后者具有软化性质的非线性关系,且煤柱与充填体具有不同的物理力学参数。充填体应力σ1与应变ε1及损伤变量D1之间存在关系:

式中:D1=1-e-ε1/ε01;ε1为充填体的变形量;ε01为峰值载荷作用下充填体的变形量;E1为充填体的弹性模量。
复合结构塑性区载荷ps与势能Vs分别为:
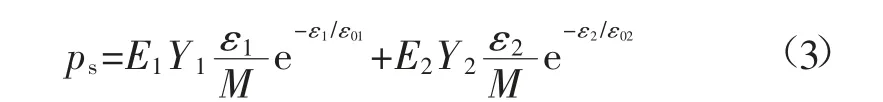
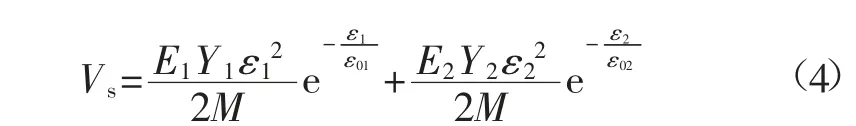
式中:ε2为煤柱变形量;ε02为峰值载荷作用下煤柱的变形量;E2为煤柱弹性模量。
复合结构弹性核区载荷pe与势能Ve分别为:
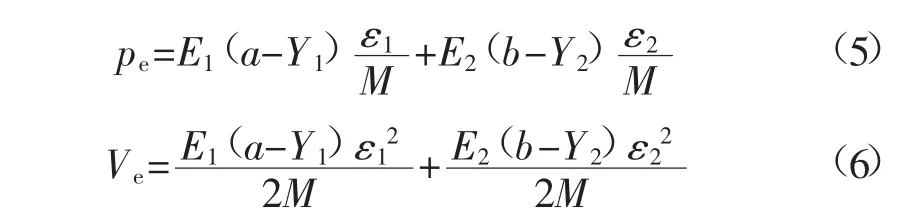
覆岩下沉产生的重力势能Vp为:
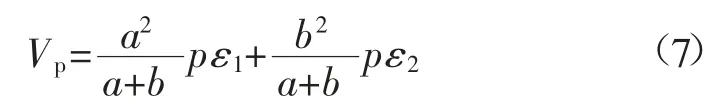
复合结构总势能为:

2 “充填体-煤柱”复合结构突变机理
2.1 数学模型
突变理论是1 门研究控制变量发生改变导致状态变量发生突变的非线性科学,可用来分析自变量的连续改变导致系统发生突变失稳的过程[20]。针对巷式充填开采复合结构突变失稳机理的分析,状态变量为一维变量,即复合结构破坏失稳。由于煤(岩)破坏的不可逆性,应选择状态不可逆转的折叠型突变模型或燕尾型突变模型。考虑到复合结构稳定性受采矿地质条件、采场巷道采掘的相互扰动,以及复合结构的组成等因素影响,选择控制变量维数更高的燕尾型突变模型,用来研究复合结构突变失稳机理。
燕尾型突变模型的势函数f(x)为:
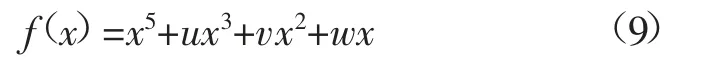
式中:u、v、w 为控制变量;x 为状态变量。
平衡曲面方程为:

突变点集为:
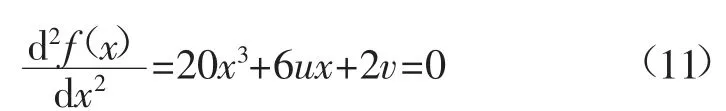
分歧点集U 为:
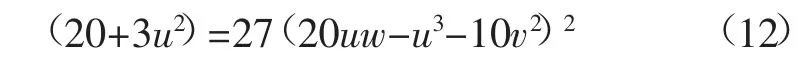
燕尾型突变分歧点集U 将三维控制空间划分成5 个区域,分别是燕翅上方、燕尾内部、燕尾下部、左燕翅下方及右燕翅下方。发生突变的必要条件为,控制变量所确定的点(相点)随时间的变化穿过了分歧点集U 的不同区域,并且它们所在区域平衡点的性质发生了变化。可采用一元四次方程实根判别方法,研究各区域相点的性质是否相同。
2.2 突变失稳临界条件
由于充填体物理力学性质、煤层厚度及强度等参数对复合结构静载稳定性产生影响。根据前期的研究工作,已得出保证复合结构静载稳定的充填体物理力学参数[7]。在此基础上,基于燕尾型突变理论,分别进行求解充填体承载部分与煤柱承载部分势能突变临界条件。
充填体承载部分复合结构势能函数V1为:

式中:o 为数学符号,表示高阶无穷小。
取无量纲量x=ε-2ε01作为状态变量,且式(14)中的余项近似取0。构建燕尾型突变平衡曲面方程,并整理为标准形式,得:

采充过程中,将导致式(17)中v 和w 发生变化。充填体承载部分,发生突变失稳的必要条件是判别式Δ1<0。已知a+b=nL,假设a=αL(α=0,1,2,…,n),式(17)可整理成关于Y1的一元二次方程,即:
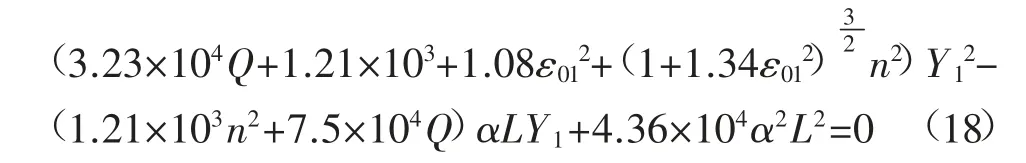
其中:Q=(6nH+6H-5L)2ε012α4L4
式(18)的判别式满足Δ01>0。判别式中对比含有Q 的各项系数,当系数之间相差至少2 个数量级时,只保留较高次幂系数的项。Δ01>0 时,表达式化简可得:
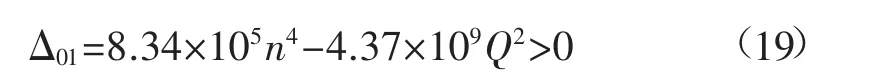
同理可得,煤柱承载部分,系统发生突变的必要条件是:
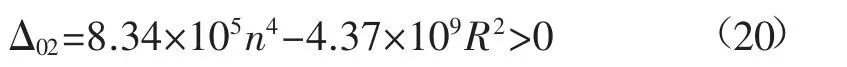
其中:R=(6nH+6H-5L)2ε022(n-α)4L4
求解式(18)和式(20)并取有意义的解集,可得复合结构保持稳定的必要条件是充填体与煤柱塑性区宽度应同时满足:
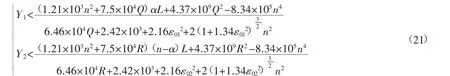
3 “充填体-煤柱”复合结构影响因素
根据式(21),复合结构发生突变失稳的影响因素主要包括采场巷道宽度L、煤层埋深H 以及开采阶段数N 等。开采阶段可解释为:巷式充填开采或连采连充过程中,通常采用多轮次循环开采的方式回收煤柱,每个循环轮次成为1 个开采阶段。以塑性区宽度作为评判标准,分别求解充填体承载部分和煤柱承载部分发生突变失稳的临界条件[22]。一般采场巷道宽度L 取4~7 m,煤层埋深L 取200~800 m,以及开采阶段数N 取2~5。根据前人的研究成果,复合结构维持稳定的临界核区率取65%[23],得到的充填体与煤柱承载部分的稳定性临界曲面如图3和图4。
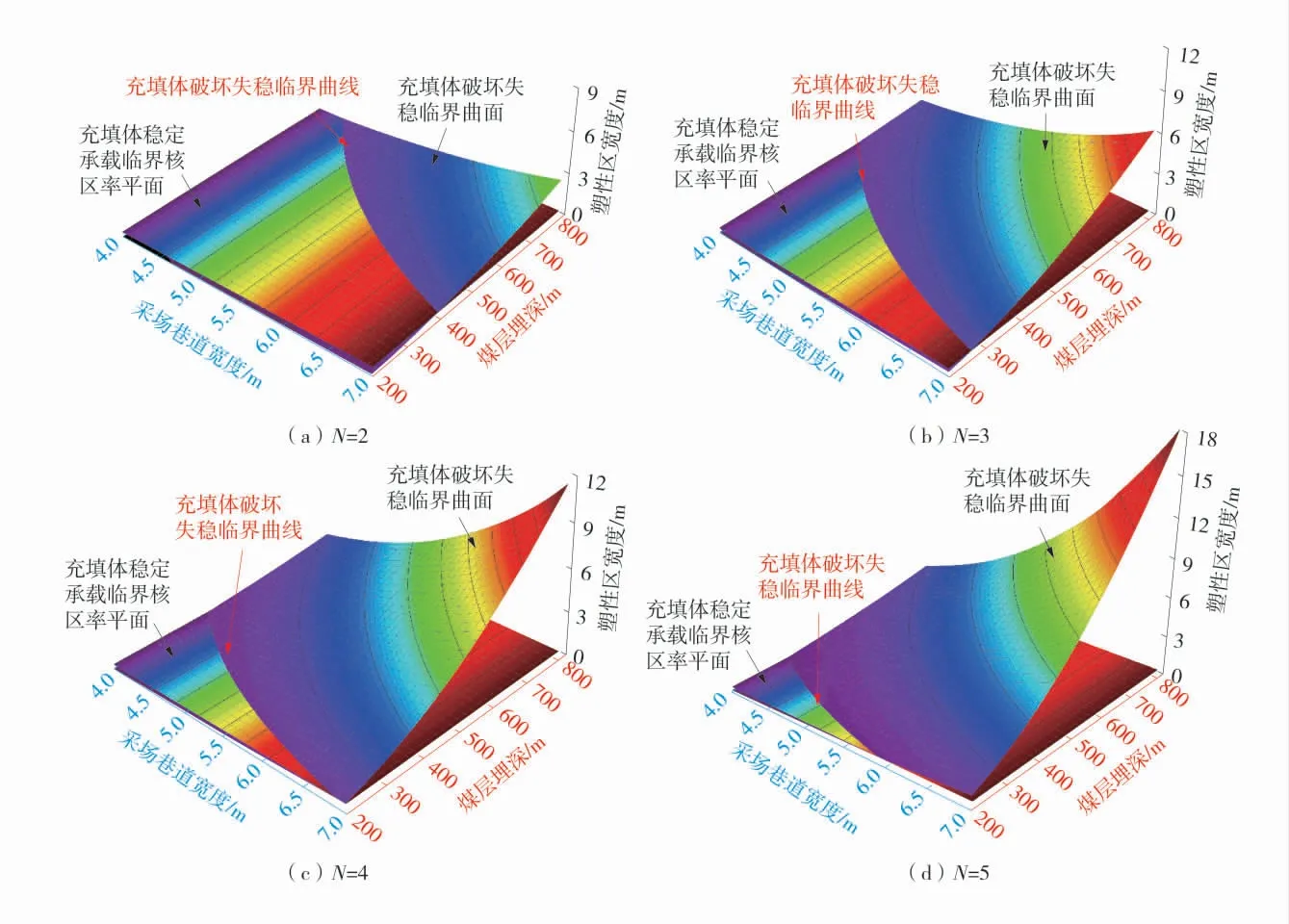
图3 充填体承载部分突变失稳临界曲面Fig.3 The catastrophe instability critical surfaces of the filling body part
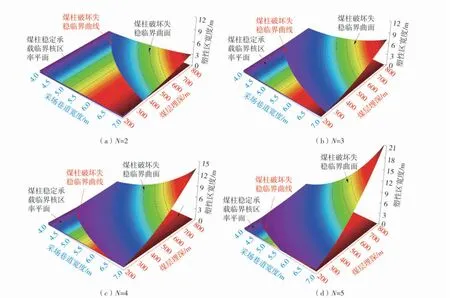
图4 煤柱承载部分突变失稳临界曲面Fig.4 The catastrophe instability critical surfaces of the coal pillar
若以采场巷道宽度作为不变量,复合结构保持稳定的最大允许煤层埋深随开采阶段数的增加而降低。这一结果表明,充填体突变失稳是临近采场巷道采掘对充填体产生反复扰动,致使其内部累计损伤的结果。开采阶段数对充填体内部损伤的影响表现为扰动次数,采场巷道宽度表现为扰动距离。若以煤层埋深作为不变量,开采阶段数越大,复合结构保持稳定的最大允许采场巷道宽度越小。这一结果表明,减小空顶面积可减低充填体内部损伤值的累积程度。若以开采阶段数作为常量,复合结构保持稳定的最大允许煤层埋深与最大允许采场巷道宽度近似呈负指数函数关系,可表示为H=λeζL,采场结构突变失稳临界拟合曲线的待定参数见表1 和表2。其中,R2表示拟合曲线与计算结果的相关程度。
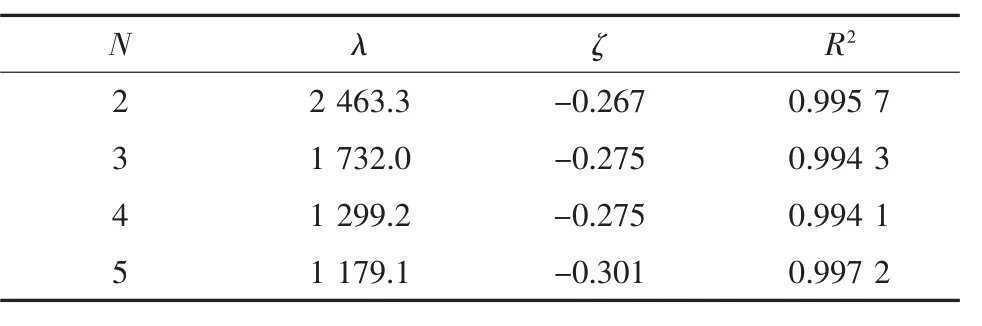
表1 充填体承载部分拟合参数Table 1 The fitting parameters in the filling body part
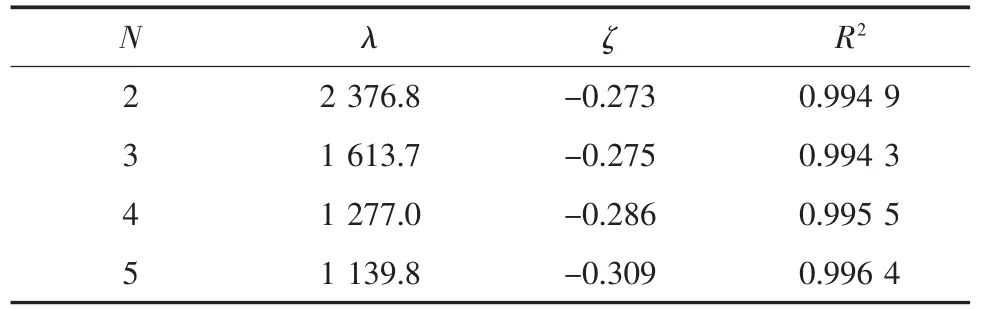
表2 煤柱承载部分拟合参数Table 2 The fitting parameters in the coal pillar part
对比上述结果发现,相同地质与开采条件下,煤柱承载部分复合结构发生突变失稳的临界曲线始终位于充填体承载部分的下方,表明煤柱较充填体更易发生破坏失稳。这一结果可解释为充填体刚充入采空区时处于散体状态,只有当充填材料凝固以及覆岩运移对充填体产生挤压,充填体才逐渐承载。而原岩应力下,煤柱处于三向受力状态,当采场巷道采掘后,煤柱的侧向压力解除,采动卸荷作用对煤柱造成了第1 次损伤。顶板下沉的初始阶段,主要由煤柱承担覆岩载荷,直到充填体与煤柱能够复合承载,覆岩运移对煤柱造成了第2 次损伤。从复合结构的承载过程来看,充填体是以覆岩运移为前提的被动承载过程,而煤柱承载是受采动卸荷与覆岩运移的逐渐损伤过程。
4 工程案例验证
王台铺煤矿开采煤层为XV 煤,煤层平均厚度2.4 m,倾角1°~2°。研究区域工作面走向长度330 m,倾向长度160 m,埋深220 m。工作面内双翼布置采场巷道,采场巷道与运输主巷夹角为50°,采场巷道宽度为6 m,划分为4 个开采阶段,复合结构宽度为18 m,即开采参数为N=4,L=6 m,H=220 m。
将实际开采的工作面进行简化处理:①巷式充填开采具有周期性,模拟全部采场巷道的采掘与充填得到的是周期性的数据;②建立的力学模型将复合结构承载特征简化为平面应变问题,采场巷道长度选取适当即可;③采场巷道尺寸远小于工作面尺寸。
建立尺寸为400 m(长)×400 m(宽)×230 m(高)的数值计算模型,工作面尺寸为120 m(走向)×100 m(倾向),走向和倾向边界煤柱分布为140 m 和150 m。覆岩采用Mohr-Coulomb 模型,充填体与煤层采用strain-softening 模型。
4.1 应力分布特征
各开采阶段连采连充期间,沿工作面推进方向煤柱与充填体上方垂直应力分布如图5。
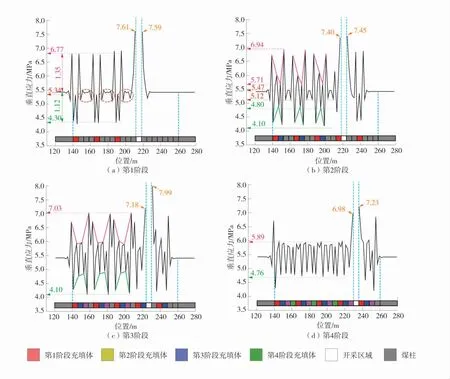
图5 复合结构垂直应力分布特征Fig.5 Vertical stress distribution characteristics of composite structure
由图5 可以看出:垂直方向的原岩应力为5.42 MPa。巷式充填过程中,垂直应力沿工作面推进方向呈周期性分布,周期长度为开采阶段数与采场巷道宽度的乘积。由于应变软化作用,充填体边界为应力降低区,并向内部延伸过程中逐渐恢复;煤柱边界出现应力集中现象,向内部延伸过程中先降低再逐渐恢复。
4.2 塑性区分布特征
各开采阶段结束,煤柱与充填体上方塑性区分布如图6。
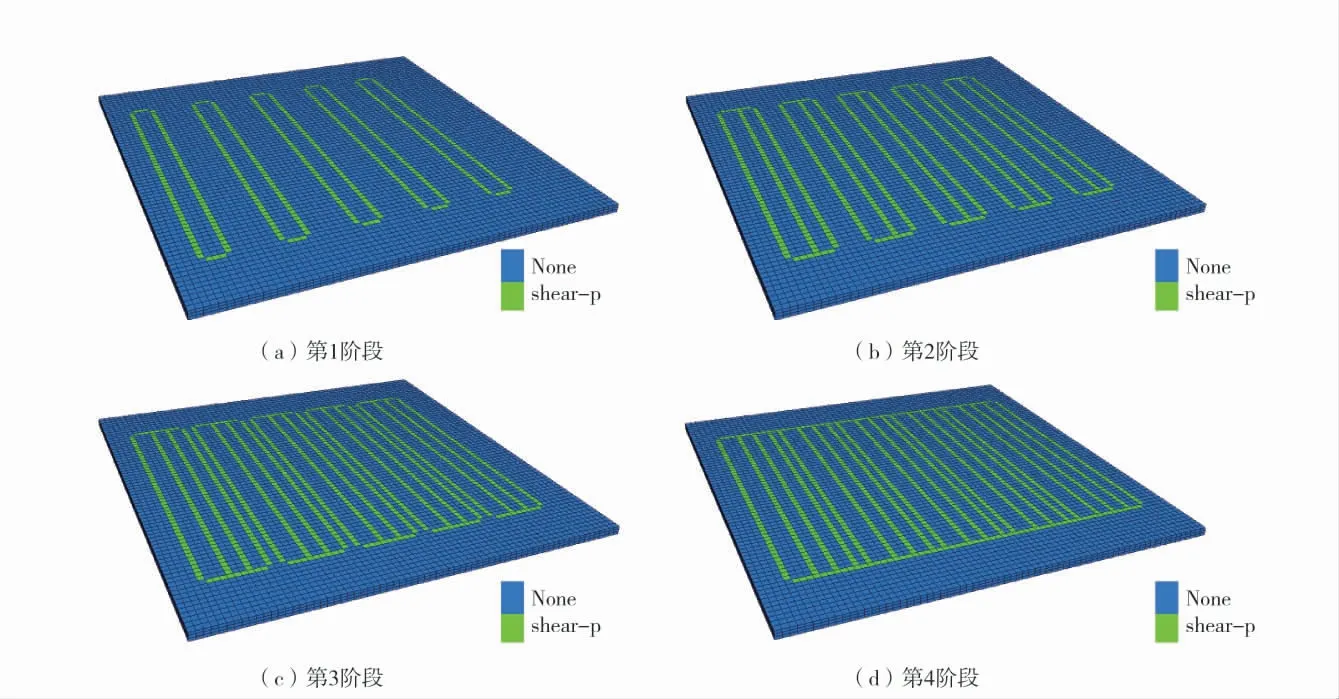
图6 复合结构内塑性区分布特征Fig.6 Distribution characteristics of plastic zone of composite structure
由图6 可以看出:煤柱与充填体的破坏形式为剪切破坏;第1 阶段结束,剪切破坏发生在煤柱边缘,而充填体内未发现破坏;第2、第3 阶段结束,在新充入的充填体约束边界处,产生新的剪切破坏,靠近充填体一侧,剪切破坏发生在第2 阶段充填体上,靠近煤柱一侧,剪切破坏发生在煤柱上;第4 阶段结束,剪切破坏位置发生在新充入的充填体两侧,位置与第3 阶段剪切破坏的位置一致;塑性区位置对应于煤柱边界的垂直应力集中位置和充填体垂直应力的谷值位置。
4.3 垂直应力对复合结构稳定性的影响
分别提取上述4 个开采阶段结束后采场最大垂直应力、复合结构上方最大垂直应力差值及复合结构塑性区宽度的数值计算结果,复合结构垂直应力变化与塑性区宽度相关性如图7。
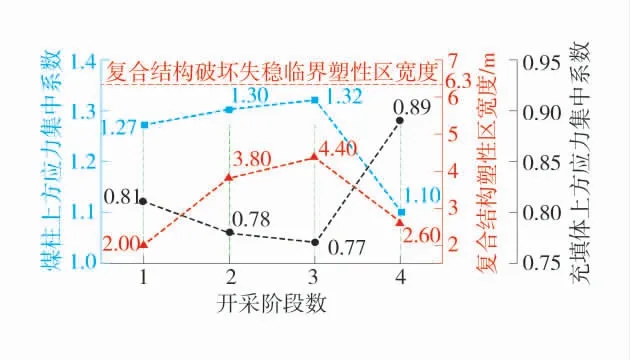
图7 复合结构垂直应力变化与塑性区宽度相关性Fig.7 Correlations between vertical stress variation and plastic zone width of composite structure
由图7 可以看出:复合结构塑性区宽度与最大垂直应力差值之间存在相关性,二者的相关系数约为0.91。垂直应力差值越大,复合结构塑性区宽度越接近采场失稳的临界值,表明采场内垂直应力的不均匀分布是导致采场发生突变失稳的主要原因;整个采充过程中,复合结构最大垂直应力相对稳定,在1.33~1.47 倍原岩应力之间,而采场内的变量似乎只有复合结构的成分(煤柱由充填体逐步置换)。由于充填体属于被动支撑结构,采场巷道开采后覆岩应力首先作用在煤柱上方,然后随着充填体、煤柱及覆岩的相互作用发生转移。
因此,煤柱尺寸越小,复合结构上方垂直应力差值越大,采场结构越容易发生突变失稳,且突变失稳更易发生在煤柱承载部分,这与图3 和图4 的计算结果相吻合。
5 结 语
1)分析了“充填体-煤柱”复合结构承载特征,建立了复合结构总势能平衡曲面方程,基于燕尾型突变状态变量属性与平衡曲面方程实根数之间的关联性,得出了以塑性区宽度为指标的复合结构破坏失稳的判别公式。
2)分析了采场巷道宽度、煤层埋深以及开采阶段数等开采参数对复合结构稳定性的影响,绘制了三者共同作用下复合结构破坏失稳临界曲面,结果表明,相同地质条件与开采条件下煤柱较充填体更易发生破坏失稳。
3)分析了复合结构承载过程中垂直应力及塑性区分布特征,发现复合结构塑性区宽度与最大垂直应力差值之间存在相关性,二者的相关系数约为0.91,垂直应力差值越大,塑性区宽度越接近复合结构破坏失稳的临界值。
4)结合工程案例,复合结构最大垂直应力在1.33~1.47 倍原岩应力之间,塑性区宽度约为2.0~4.4 m之间,巷式开采过程中,复合结构核区率始终不低于75.6%,破坏失稳判别公式的准确性得到了验证。

