基于改进DCGAN 的电力系统暂态稳定增强型自适应评估

李宝琴，吴俊勇，强子玥，覃柳芸，郝亮亮

（北京交通大学电气工程学院，北京市 100044）

0 引言

暂态稳定性是指当系统遭受到大扰动时，各同步发电机保持同步运行的能力［1］。随着高比例新能源并网，高比例大功率电力电子装置以及高比例新型负荷接入电网，复杂多变的动态特性给电力系统带来诸多挑战［2-3］。其中，暂态失稳是很多大电网停电的主要因素［4］，快速、准确、可靠的电力系统暂态稳定评估是系统安全稳定运行的重要保障。

传统的暂态稳定分析方法包括时域仿真法、直接法等，但面对复杂电网时无法同时满足计算精度和速度的要求。飞速发展的数据驱动和深度学习技术，依靠强大的特征提取和数据挖掘能力，为电力系统暂态稳定评估提供了新的思路。目前已有很多相关的研究成果，包括支持向量机（support vector machine，SVM）［5-6］、决策树 和随机森林（random forests，RF）［7］、深度置信网络（deep belief network，DBN）［8-10］、卷积神 经网络（convolutional neural networks，CNN）［11-12］以及长短期记忆网络［13］等。

但是，电力系统在绝大多数情况下处于正常运行的状态，继电保护装置日趋完善，暂态失稳情况极少，给通过数据挖掘方法来进行暂态稳定预测带来极大的挑战。其次，对失稳样本的漏判与对稳定样本的误判代价往往不同，在实际应用中，更为关注失稳样本。为解决这一矛盾，在算法层面，文献［14］提出一种代价敏感的暂态稳定评估方法，在损失函数中增加对失稳样本漏判的权重系数，改善了模型训练结果的倾向性情况，但是稳定样本的误判率也会随之提高。文献［15-16］在模型训练过程中采用焦点损失函数，对重叠区域的难分类样本进行处理，提高了暂态稳定评估全局准确率。文献［17］采用2 个DBN，将判别结果不一致的样本划分为不确定样本，减少了对失稳样本的漏判，但是随着评估结果的细致化，响应时间也随之增加。在数据层面，文献［18］采用自适应合成抽样（adaptive synthetic sampling，ADASYN）和降噪自编码器相结合的方式改善样本不均衡情况，但其样本数量有限，缺乏说服力。文献［19］基于改进条件生成对抗网络（conditional generative adversarial network，CGAN）对样本进行增强，提升了暂态稳定评估的正确率，但是网络拓扑结构变化后的继承性并未研究。针对拓扑结构改变前训练模型在拓扑变化后很可能不再适用，文献［20］提出一种最小均衡样本集的变步长生成方法对预训练模型进行迁移，但是当系统规模增加、线路条数增多时，均衡样本集的搜索将耗费大量时间。文献［21］针对故障发生前的动态安全稳定评估问题，将在一种预想故障集下得到的模型迁移至多种预想故障集，有效提高了预测效率和预测精度。文献［22］采用增量学习和迁移学习方法解决了电力系统过渡阶段的样本匮乏问题。

为了弥补上述研究中存在的不足，同时考虑样本不均衡特性和模型的自适应性，本文提出了一种基于改进深度卷积生成对抗网络（deep convolutional generative adversarial network，DCGAN）的稳定评估方法。设计了由CNN 构成的生成器和判别器结构，使用Wasserstein 距离替换原模型中的损失函数并引入谱归一化，得到稳定的网络结构，生成符合真实失稳样本分布的增强样本，解决了样本不均衡问题。拓扑结构变化时，采用样本迁移、模型微调和改进DCGAN 增强技术，解决了迁移学习的样本选择和生成的问题，实现了电力系统暂态稳定增强型自适应评估。

1 DCGAN 基本原理

生成对 抗网络是由Goodfellow［23］在2014 年 提出的。它是一种无监督学习算法，其基本结构见附录A 图A1。

DCGAN 将CNN 和生成对抗网络进行结合。把反卷积网络和卷积网络分别引入到生成器G和判别器J中进行无监督的训练，利用CNN 强大的特征提取能力来提高生成网络的学习效果。DCGAN 的训练过程是一个二元零和博弈问题［24］。博弈过程中的损失函数如式（1）所示。

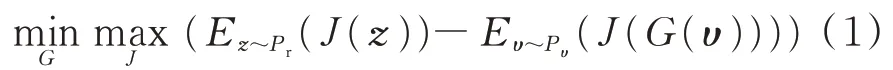
式中：z为真实的输入样本；υ为生成器输入的噪声数据；Pr为概率分布；Pυ为υ的概率分布；Ez～Pr(J(z))和Eυ～Pυ(J(G(υ)))分别为输入样本和噪声的期望值。

通过不断博弈抗衡，生成器可以有效地提高自身的失稳样本生成能力，学习到原始数据的分布，可视为一种能够用于数据合成的非线性插值方法，适合解决基于机器学习的电力系统暂态稳定预测样本不平衡问题。

2 改进DCGAN

2.1 损失函数的改进

传统DCGAN 采用的是JS（Jensen-Shannon）散度，在对抗训练的过程中，容易发生梯度消失、模式崩溃等问题［25］，而本文使用Wasserstein 距离替代JS散度作为优化目标，引入梯度惩罚项，大幅提升训练的稳定性。

Wasserstein 距离的定义如式（2）所示。

式中：W(Pr，Pg)为Wasserstein 距离；y为样本；Pg为概率分布；Π(Pr，Pg)为Pr和Pg的联合概率分布集合；δ为Π(Pz，Py)中的元素；E(z，y)～δ(||z-y||)为样本对距离的期望值，在所有可能的联合概率分布中能够对这个期望值取到下界inf 就是Wasserstein 距离。

根据Kantorovich-Rubinstein 定律［26］，Wasserstein距离的求解一般采用其对偶形式，如式（3）所示。

式中：f(z)为判别器的映射函数；||f(z)||L为f(z)的L范数；k为Lipschitz 常数，||f(z)||L≤k表示函数f(z)满足k-Lipschitz 连续条件。

2.2 谱归一化

2.1节中为了满足Lipschitz 连续性的条件约束，规定参数矩阵中的元素不得大于k值，这种方法简单有效，但是也导致参数矩阵的结构不稳定。而谱归一化能够在满足Lipschitz 连续性的条件下，维持参数矩阵的稳定。

对于多层神经网络而言，其输入和输出的关系如式（4）所示。

式中：xn、wn、bn分别为神经网络第n层的输出、权重以及偏置；an(·)为激活函数，可以采用ReLu 或者Leakey ReLu 函数。

为了便于推导，省去偏置bn，则式（4）可表示为：

式中：Hn为对角矩阵，用来表示激活函数的作用。多层网络的输出关系如式（6）所示。

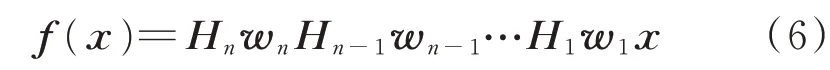
在满足Lipschitz 连续条件时对f(x)的梯度∇x(f(x))提出了新的要求，如式（7）所示。

式中：||·||2为谱范数。

σ(w)为矩阵w的最大奇异值。对于对角矩阵H，有σ(H)=max(h1，h2，…，hn)，其 中h1，h2，…，hn为H的奇异值。因此式（7）可以写成：

为了让f(x)满足Lipschitz 连续性的约束，需要对其梯度进行归一化处理，如式（9）所示。

由此可知，只要让参数矩阵中的每个元素除以其谱范数，即谱归一化，就可以满足Lipschitz 连续性的约束，此时Lipschitz 常数为1，从而解决了因直接限制参数带来的波动问题。在算法实现时，采用幂迭代法求解w的奇异值，可以减少计算资源的消耗。

3 基于改进DCGAN 的失稳样本增强方法

暂态功角稳定的实质是发电机能否保持同步运行。文献［27］的研究结果表明，发电机的功角轨迹几何特征具有集束性和趋同性，能够清晰地反映系统的稳定特性，并且输入维度不会随着系统规模的扩大而增加，有利于后续迁移方案的实施。因此，本文选取故障切除后发电机的功角轨迹簇特征作为模型的输入，其详细的定义见附录A 表A1。

3.1 迁移学习技术

基于机器学习的暂态稳定评估方法，在离线训练时往往是针对特定拓扑结构进行的。而当拓扑结构或运行方式发生较大变化时，针对拓扑变化前训练得到的分类模型很可能不再适用。实际电网规模十分庞大，重新生成用于模型训练的样本集并训练得到适用于当前拓扑的分类模型，往往非常耗时。因此，本文通过迁移学习微调（fine-tuning）原分类模型的参数，使其能够在新的运行方式下仍然具有较好的评估效果。参数微调是迁移学习的一种手段，将源域中训练好的原模型的网络结构和所有参数全部迁移至新的模型，即作为目标域下新模型的初始值，可减少分类模型的训练时间。在上述模型迁移的基础上，利用目标域下的新训练集微调网络，快速得到适用于目标域的分类模型。以DBN 为例，其模型迁移及微调过程见附录A 图A2。

迁移方案的实施离不开目标域下的新样本集，为了减少目标域下的样本生成时间，文献［20］提出了一种最小均衡样本集的生成方法。文献［28］采用关键故障持续时间原则和关键故障位置原则生成新样本，但是随着实际系统规模的增加和线路条数的增多，目标域样本集的数量也会大大增加，不利于迁移方案的实施。因此针对目标系统，本文首先随机快速生成少量的样本，然后考虑到源域系统运行时间较长，积累了大量的暂态稳定样本数据，再利用样本迁移将源系统中的数据处理后应用于目标域系统。从源系统中选择可迁移的样本是一个样本距离排序问题，其计算公式如式（10）所示。

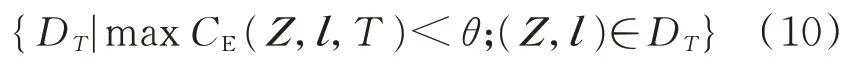
式中：DT为可迁移的样本集；CE(Z，l，T)为欧氏距离计算函数；Z为源域样本的输入特征；l为源域样本的标签；θ为预设值；T为目标域少量样本集。

当样本集符合所有元素和目标域样本集的最大欧氏距离小于阈值时，该样本集为可迁移样本集。将DT和在线生成的少量样本集合并，考虑到源域系统以及目标域系统的样本不均衡导致模型更新过程中的倾向性问题，通过改进DCGAN 对失稳样本进行增强，最终得到正负均衡的样本集对原模型进行微调，得到适用于目标域系统的暂态稳定预测模型，有效地解决了迁移学习的样本生成耗时和样本选择问题。样本迁移及增强的过程如图1 所示。

图1 样本迁移及增强过程示意图Fig.1 Schematic diagram of sample transfer and enhancement process

3.2 增强型自适应评估流程

为了解决暂态稳定评估中样本不均衡以及迁移学习样本的选择和生成问题，本文提出了一种基于改进DCGAN 的暂态稳定增强型自适应评估方法，包括离线数据增强训练、模型更新增强迁移、在线评估这3 个部分，如图2 所示。

图2 增强型自适应评估过程Fig.2 Enhanced adaptive assessment process

1）离线数据增强训练

步骤1：由于历史运行样本数量有限，主要借助时域仿真生成大量样本并贴上对应的标签。对故障切除后的发电机功角提取27 个轨迹簇特征，并对其进行最大、最小归一化处理。

步骤2：将预处理完后的样本按一定的比例划分训练集、验证集和测试集。根据预训练模型在验证集上的性能选择合适的网络结构和参数，测试集在整个训练过程中是未知的，仅用于模型最终性能的测试。

步骤3：从训练集中筛选出失稳样本，生成器和判别器采用交替对抗训练的方式，在每次训练中先训练5 次判别器，再训练1 次生成器。生成器的输入为满足高斯分布的噪声数据υ（维度等于100），每迭代1 次即可生成1 组增强失稳样本，将其和真实失稳样本一起作为判别器的输入，根据式（3）计算损失函数值，采用变步长自适应学习率的Adam 优化算法对改进DCGAN 模型的网络权重和偏置进行更新，初始学习率为0.000 2。采用增强训练后的分类模型对验证集性能进行评价，选取综合指标值最高的生成样本集增强到原始训练集中，从而得到正、负样本均衡的训练集对暂稳评估模型进行训练。

2）模型更新增强迁移

步骤1：当系统发生一些预料之外的变化时，针对目标域系统快速生成少量样本，并对这些样本进行预处理。根据式（10）计算源系统中的训练集和目标域样本集的距离并排序，根据需要选择合适的阈值θ，从而确定可迁移的样本，其和目标域的样本集一起构成迁移样本集。

步骤2：采用改进DCGAN 方法对迁移样本集中的失稳样本进行数据增强，同样选取综合指标值最高的生成样本增强到迁移样本集上，得到均衡的增强迁移样本集。利用模型迁移将源系统训练好的分类模型迁移至目标域并对其参数进行微调，得到适用于当前运行方式并更新好的模型。

3）在线评估

在线应用时，读取实时同步相量测量单元（synchrophasor measurement unit，PMU）数据，采用基于可信度的分层实时预测［9］和样本增强相结合的方法，进行暂态稳定动态实时评估。

3.3 性能评价指标

暂态稳定是一个典型的非平衡分类［29］问题，稳定样本的标签为（1，0），失稳样本的标签为（0，1）。仿真时间内，任意2 台发电机的转角差大于360°的样本为失稳样本，反之则为稳定样本。采用2×2 混淆矩阵评价算法得到的分类效果，如表1 所示。其中μs和γus分别为稳定样本被正确或错误预测的数目，μus和γs分别为不稳定样本被正确或错误预测的数目。特别是在电力系统暂态稳定预测问题中，更关注失稳样本。

表1 统计结果Table 1 Statistical results

评价指标包括分类准确率Acc（正确预测的样本占所有样本的比例）、稳定样本识别准确率ηSR（正确判断为稳定的样本占所有稳定样本的比例）、失稳样本识别准确率ηUR（正确判断为失稳的样本占所有失稳样本的比例），以及综合指标Omean（ηSR和ηUR的几何平均数），具体计算公式分别如式（11）至式（14）所示。

4 算例分析

为了验证本文所提增强型自适应评估方法的有效性，在Tensorflow1.13 环境下搭建改进DCGAN模型，基本结构和参数设置见附录B 图B1 及表B1。PC 配置为：Intel Core i7-8565u CPU、8GB RAM，编程语言为Python。使用MATLAB 工具箱中Power System Too（lPST）3.0 进行暂态稳定样本批仿真。算例系统采用IEEE 39 节点系统以及IEEE 140 节点系统。

4.1 样本集的生成

IEEE 39 节点系统包含10 台发电机、39 条母线和46 条线路。考虑在75%～120%负荷水平范围内以5%为变化步长生成10 种负荷水平；在不含有变压器的线路上设置故障，以10%为变化步长在每条线路的0%～90%区间设置故障点，故障类型设为最为严重的三相短路故障；故障清除时间考虑故障后0.016～0.183 s，以0.016 s 为变化步长的11 种故障切除时间，仿真时间为5 s，总共生成37 400 个样本。

IEEE 140 节点系统包含48 台发电机、140 条母线和233 条线路，系统频率为60 Hz。负荷水平依然是在75%～120%负荷水平范围内，以5%为变化步长；故障清除时间考虑故障后0.083 s 清除近端故障，0.100 s 清除远端故障或者0.150 s 清除近端故障，0.167 s 清除远端故障，共生成25 045 个有效样本。

上述样本集覆盖了电力系统可能的典型运行工况，对分析暂态稳定评估问题而言是充足有效的。为模拟实际系统中失稳样本稀少的情况，随机剔除部分失稳样本，保证总样本数目和失稳样本数目的比例约为20∶1［30］。按3∶1∶1 划分训练集、验证集和测试集，各集合中稳定、失稳样本的组成如表2所示。

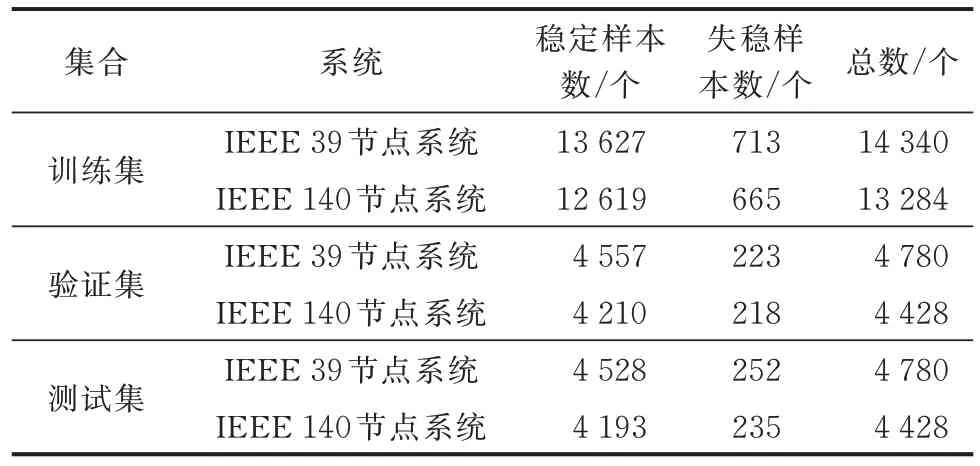
表2 不同算例系统样本集合的构成Table 2 Composition of sample sets for different case systems

4.2 DCGAN 改进效果分析

为了分析DCGAN 的改进效果，以IEEE 39 节点系统为例，判别器和生成器的损失函数随迭代次数的变化如图3 所示。

图3 改进前后损失值的变化Fig.3 Change of loss value before and after improvement

从图3 可以看出，改进前采用JS 距离作为损失函数，DCGAN 模型存在梯度消失和模式坍塌问题，生成器和判别器训练过程中参数值难以稳定，波动较大，没有收敛的趋势，此种现象难以训练出高质量的增强失稳样本。而采用Wasserstein 距离对损失函数进行改进后，在迭代35 次以后，训练过程整体呈稳定趋势，波动幅度较小。说明损失函数采用Wasserstein 距离比JS 距离在训练过程中更加稳定，效果更好。进一步对卷积层的参数进行谱归一化，在第10 次迭代时就可以保持稳定，无大幅振荡现象，并且其生成器的损失值最小，在0 附近波动，说明改进DCGAN 不断逼近真实失稳样本的分布，从而验证了改进DCGAN 的有效性。

为了进一步说明生成失稳样本和真实失稳样本之间的关系，使用弗雷歇距离（Frechet inception distance，FID）来评价生成失稳样本和真实失稳样本分布间的相似度。FID 因考虑了路径空间距离，所以对有一定空间时序性的曲线进行相似度评价更具有原则性和综合性。发电机功角动态轨迹曲线具有时序性，因此采用FID 来评价生成样本和真实样本分布的相似度是合理的。IEEE 39 节点系统和IEEE 140 节点系统在采用DCGAN 改进前后的FID 如表3 所示。FID 越小，表明样本分布间的相似度越高，采用改进DCGAN 后的FID 相较于改进前有明显的降低，分别降低了大约23.1%和41.3%，进一步验证了改进后的DCGAN 在提升生成失稳样本质量上的有效性。

表3 改进前后FID 对比Table 3 Comparison of FID before and after improvement

4.3 离线增强训练效果

为了分析基于改进DCGAN 的数据增强方法应用于电力系统暂态稳定预测样本不均衡问题的效果，采用随机过采样（random oversampling，ROS）、合成少数类过采样（synthetic minority oversampling，SMOTE）和自适 应合成抽样（adaptive synthetic sampling，ADASYN）这3 种常用的数据增强算法与其进行对照，所有算法都设定为增强训练集中稳定样本数目等于失稳样本数目，因此采用改进DCGAN 生成失稳样本的数目等于原始训练集中稳定样本数目减去失稳样本数目。分类模型采用RF 和DBN，RF 采用90 棵树进行集成，DBN各层神经元的结构为［27，200，100，50，30，2］。本文样本的采样时间间隔为0.016 s，以故障切除后第0.166 s 的数据集为例进行分析和验证，表4 和表5给出了算法在不同模型及不同算例系统上的测试效果。

从表4 和表5 可以看出，由于原始训练集中失稳样本极少，导致模型对失稳样本的识别率ηUR很低。采用不同的数据增强算法均能在一定程度上改善模型的ηUR指标，而基于改进DCGAN 的数据增强算法相比于传统方法拥有更高的可靠性、更大的Omean和预测准确率，同时保证了对稳定样本的识别率不至于太低。以DBN 为例，2 个算例系统在增强后的训练集比原始数据的ηUR分别提高了6.74%和8.58%，Omean分别提高了3.04% 和2.98%。这表明改进DCGAN 合成的失稳样本和真实失稳样本的分布更相近，提高了对失稳样本的识别准确率，实现了小样本在分类器中的稳定训练。

表4 IEEE 39 节点系统各种数据增强算法性能对比Table 4 Performance comparison of various data enhancement algorithms in IEEE 39-bus system

表5 IEEE 140 节点系统各种数据增强算法性能对比Table 5 Performance comparison of various data enhancement algorithms in IEEE 140-bus system

为了进一步分析不同数据增强算法的效果，将各类算法的合成样本采用t 分布随机近邻嵌入（tdistributed stochastic neighbor embedding，t-SNE）［31］工具降维到二维平面上进行可视化。从图4 可以看出，ROS 仅仅是将少数类的失稳样本进行简单的复制以增加失稳样本的数目，样本间大量的重叠，容易造成过拟合问题。SMOTE 是基于线性插值的方法，在2 个失稳样本连线上随机选取1 个点作为新的少数类样本。ADASYN 在最近邻分类器被错分类的原始样本附近生成新的少数类样本，自适应合成靠近稳定边界的样本，所以增强效果略优于SMOTE。改进DCGAN 并不是对原始样本简单的复制与拼接，是一种基于分布的学习算法，学习到了真实的样本分布规律，在状态空间中生成了全新有效的新样本作为原始样本的补充。从增强后的评估性能来看，在4 种数据增强算法中，改进DCGAN 的可靠性、Omean及Acc均最高，有效减少了对失稳样本的漏判。因此从数据合成方式和合成性能上比较，改进DCGAN 更加适用于电力系统的失稳样本均衡问题。

图4 不同数据增强算法样本分布对比Fig.4 Comparison of sample distribution with different data enhancement algorithms

4.4 在线增强迁移效果

在4.3 节中，源系统已经训练出性能较好的暂态稳定预测模型。当系统拓扑结构或运行方式发生较大变化时，采用样本迁移和改进DCGAN 增强技术，解决迁移学习样本选择和生成问题。考虑分类模型的性能以及模型迁移的便捷性，本节分类模型采用DBN。

4.4.1 拓扑变化下的迁移

针对IEEE 39 节点系统，为了模拟系统实际运行中不在调度人员预知范围内的变化，对其拓扑结构和运行方式进行修改，新增3 个目标系统，其拓扑变化及仿真设置如表6 所示。

表6 源系统和目标系统的仿真设置Table 6 Simulation settings of source system and target systems

针对不同的目标系统，随机快速生成100 个样本作为目标域少量训练样本集，其余3 200 个样本作为测试集。设置合适的θ保证从源系统中迁移的样本数为1 000，实际应用中可以根据具体需求选择θ。将迁移前、迁移样本集微调模型以及本文所提的增强迁移样本集微调模型效果进行对比，测试结果如表7 所示。从表7 可以看出，由于拓扑变化后的样本集和原模型的训练集不再是同分布的，因此直接使用拓扑变化前的模型进行评估，性能有所下降。采用样本迁移微调原模型使得Acc得到了有效的提高，但是由于迁移样本集中失稳样本极少，导致在微调过程中对失稳样本的学习不足，ηUR低于88%，无法进行在线应用。而采用改进DCGAN 对迁移样本集中的失稳样本进行增强，ηUR指标相比于迁移前最高提升了6.23%，同时Omean和Acc均保持在95%以上，实现了拓扑结构变化情况下的暂态稳定增强型自适应评估。

表7 不同迁移方案性能对比Table 7 Performance comparison of different transfer schemes

将采用改进DCGAN 合成失稳样本的时间和采用传统方法［21］通过时域仿真延长故障切除时间生成失稳样本的时间进行对比，结果如表8 所示。

表8 样本生成时间对比Table 8 Comparison of sample generation time

从表8 可以看出，采用改进DCGAN 生成增强失稳样本的时间为2 min 左右，而时域仿真法生成同样数量的样本需1 h 左右，样本生成效率提高了30 倍，显著减少了迁移学习过程中在线样本生成的时间，这对暂态稳定自适应评估的在线应用至关重要；其次，改进DCGAN 直接根据失稳样本的“轨迹簇”特征生成了全新有效的新样本特征集用于模型更新，省去了样本处理和特征提取的阶段，在线应用上具有更大的时间优势。

4.4.2 不同系统间的迁移

为了验证本文所提方法在不同系统间进行迁移的有效性，定义如下2 种场景。

场景A：将IEEE 39 节点系统作为源系统，IEEE 140 节点系统作为目标系统。目标系统少量样本集的样本数为100，测试集的样本数为4 428，迁移样本数为1 000。

场景B：将IEEE 140 节点系统作为源系统，IEEE 39 节点系统作为目标系统。目标系统少量样本集的样本数为100，测试集的样本数为4 780，迁移样本数为1 000。

采用不同方法的迁移测试结果如图5 所示。对于场景A，相比于迁移前，本文所提方法的预测准确率Acc提高了20.76%，Omean提高了11.79%。对于场景B，由于样本不均衡特性导致模型对失稳样本的识别率较低，Omean低于60%，而通过样本迁移和改进DCGAN 增强后，Omean可由57.02% 恢复至83.45%，提高了26.43%，模型可靠性得到了大幅的改善。

图5 不同迁移方案性能对比Fig.5 Performance comparison of different transfer schemes

各阶段的耗时如表9 所示，场景A 下由于源系统样本数多于场景B，因此其样本迁移过程中的距离计算耗时略长于场景B，而场景A 下所需的增强失稳样本数目少于场景B，因此其失稳样本增强时间较少。计算3 种场景下的总耗时，相比于传统方法针对新系统仿真生成大量的样本集进行模型重新训练，本文所提方法的总耗时在9 min 内，而暂态稳定预测的时间仅为0.014 ms，能够满足时效性的需求。采用改进DCGAN 模型，有效解决了在线样本生成耗时的问题，使得预训练模型在短时间内可以在规模不同的系统间进行迁移，大大提高了迁移速度，实现了不同系统间的暂态稳定增强型自适应评估。

表9 模型各阶段耗时Table 9 Time consumption at each stage

5 结语

针对暂态稳定预测中稳定样本和失稳样本比例失衡的问题，同时考虑到模型的适用性，本文提出一种基于改进DCGAN 的暂态稳定增强型自适应评估方法，在IEEE 39 节点系统和140 节点系统进行实验测试，得到如下结论：

1）采用Wasserstein 距离作为DCGAN 的损失函数并对其参数进行谱归一化，可以有效解决对抗训练过程中的梯度消失和模式崩溃问题，使得生成的增强失稳样本能够有效逼近真实失稳样本的分布；

2）改进DCGAN 的样本增强效果要优于ROS、SMOTE 和ADASYN，在状态空间内生成了全新有效的新失稳样本作为原始样本集的补充，有效减少了对失稳样本的漏判，提高了模型的可靠性；

3）采用样本迁移和微调技术，有效解决了在系统拓扑变化下的暂态稳定评估模型适用性问题，进一步采用改进DCGAN 进行失稳样本增强，显著减少了迁移学习过程中在线样本生成时间，提高了迁移速度。

由于实际系统规模庞大，暂态稳定特性更加复杂，为了更好地兼顾暂态稳定预测的快速性和准确性，进一步将分层实时预测的方法和改进DCGAN的样本增强方法相结合，完善电力系统暂态稳定增强自适应评估模型；在实际交直流大电网上对所提方法进行验证，将是下一步研究工作的重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。