浮体上浮姿态的稳定性分析与试验验证
赵桥生,方 田,肖冬林,潘广善,徐萌萌
(1.天津大学,天津 300072;2.中国船舶科学研究中心,江苏 无锡 214082)
0 引 言
由于有效容积及浮力需求,工程上浮体往往为钝体。为降低技术复杂程度及成本,也无姿态控制系统。仅通过自身浮力实现上浮,显然其水动力特性以及主体自身的静力特性(重心、浮心、重量等参数)成为影响其运动稳定性的主要因素。一旦两者匹配不当将会使航行体在上浮运动中存在“枯叶”现象,即剧烈摇晃甚至翻转,将大大影响浮体应急上浮以保障乘员生命力或仪器设备安全性的功能。所以工程上迫切需要为保证浮体上浮姿态稳定提供设计指导原则。尽管大攻角上浮钝体会产生严重分离,非线性影响较为复杂,其稳定性可能因浮体而异,可能没有一般性原则。但小攻角是大攻角必经之路,故小攻角下的稳定性准则仍然具有非常重要的工程意义,至少应该是大攻角浮体遵循的必要条件。
评价稳定性离不开浮体的水动力特性。在流线型的水下航行体数值计算研究方面的研究较多,如周广礼[1]基于粘性流场直接数值模拟方法开展了潜艇上浮运动数值模拟研究。Atkins[2]利用数值模拟手段研究了俯仰角在-16°~16°之间三个不同状态下的垂直面操纵性水动力。Roddy[3]开展了水动力CFD 技术处理其设计问题研究,其目标是为CFD 代码的验证提供一个试验数据库。Wu(2005)[4]考虑了海底对航行体的影响,研究了水下航行体在接近海底过程中的水动力数值模拟方法。林兆伟等(2016)[5]对潜器斜航拖曳、纯升沉等典型操纵运动进行了数值模拟。黄苗苗(2019)[6]基于DFBI 方法结合重叠网格技术,研究了内孤立波作用下水下航行体自由运动特性的数值模拟方法。
当然也可以对特定的浮体,将流场及运动用数值方法耦合求解来揭示它的稳定特性,但这耗时、费力,且无一般性。本文在小攻角假设下,建立了浮体上浮的姿态运动方程,给出解析解,分析姿态收敛的条件,形成了稳定性判据。通过数值计算给出了特定浮体的流体动力,并进行了上浮稳定性水池试验。试验结果反映了数值计算流体动力及稳定性判据的工程价值。
1 轴对称浮体上浮运动特性及稳定性分析
1.1 轴对称浮体上浮稳定性判据
实际使用浮体几乎均为轴对称体,研究其上浮运动及稳定性具有重要工程意义。在工程应用中,研究人员关心浮体姿态甚于浮体上浮的轨迹。事实上,当姿态非常稳定时,轨迹必然比较铅垂。在此给出了浮体上浮姿态的稳定性判据,如下所示。
浮体上浮运动坐标如图1 所示,为随体坐标系xyz-G(右手系),oo′为铅垂线,原点设在浮体的质心G上,记B为浮心,G为质心,研究xGz垂直平面中浮体上浮稳定性。浮心位于重心之上,有xB>0,浮力FB=mB·g,mB为浮体排开水的质量。设浮体受扰动,x轴与垂线oo′之间产生夹角记为倾角θ,规定绕y轴顺时针旋转θ为正(图1中方向),对应旋转角速度、对应旋转角加速度、特征长度L,攻角α遵从右手法则,图1中自上浮速度u到Gx顺时针转为正。
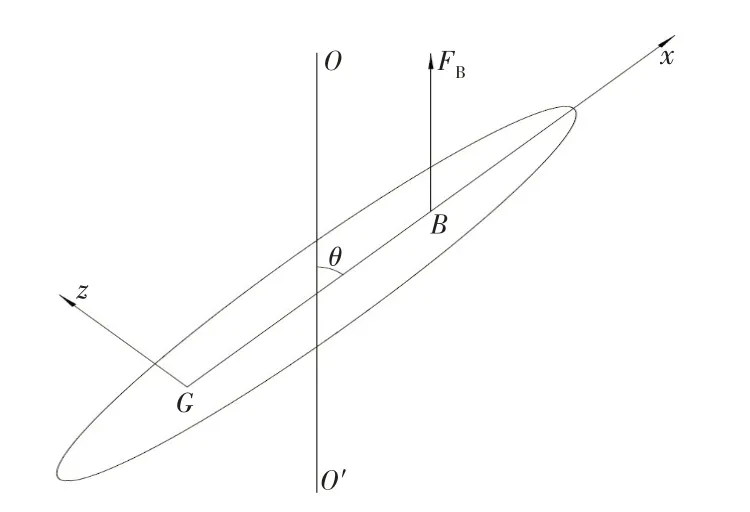
图1 浮体上浮运动坐标示意图Fig.1 Schematic diagram of buoyant body’s coordinate
则在xyz-G系中,攻角α=θ。记浮体质量为m,绕y轴惯量为Jy,附加质量为A55,上浮速度为u。M'w、M'q分别为对浮体质心的位置导数和旋转导数。对于浮体运动,动力学方程为

浮体上浮过程中,小扰动情况下有:sinα≈α,sinθ≈θ,则由方程(1)可得


其中,方程(3)中的A和B分别为

当A>0,B>0时,K>A指数发散;当A>0,B<0时,K<A指数收敛;当A<0,指数发散。
综上,按状态1和状态2可得稳定分布域,如图2所示。
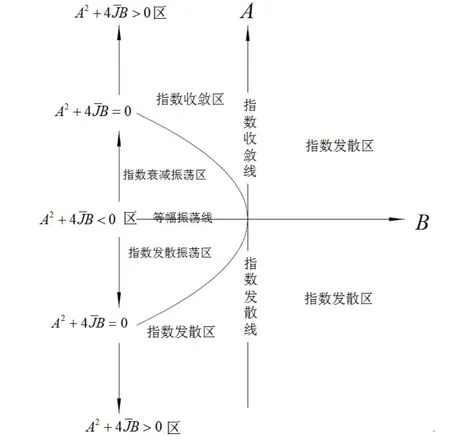
图2 稳定分布域Fig.2 Stable distribution domain
结论:A>0,B<0为运动稳定条件,即

1.2 浮体上浮运动特性
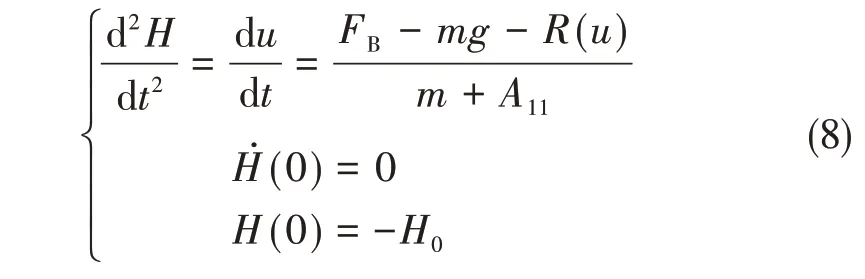
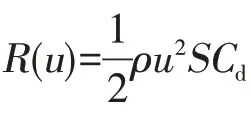

图3 浮体上浮运动坐标示意图Fig.3 Schematic diagram of buoyant body’s coordinate
亦即


微分方程(9)的解为

微分方程(8)的解为

限于纯浮力,往往浮体上浮速度达到平衡状态也不会很大,在这一区间,阻力系数Cd往往不是常数,所以公式(10)和(11)是近似解,若将实际阻力系数Cd=Cd(u)代入式(8),则可以得到精确解。
2 浮体流体动力数值计算
2.1 浮体实例的流体外形
本文研究的浮体外形为钝体,该浮体的外形及坐标系如图4所示,具体参数如表1所示。

图4 浮体示意图Fig.4 Schematic diagram of the buoyant body

表1 浮体参数Tab.1 Parameters of buoyant body
2.2 控制方程
不可压缩粘性流体连续性方程和时均化的N-S方程,如式(12)~(13)所示:
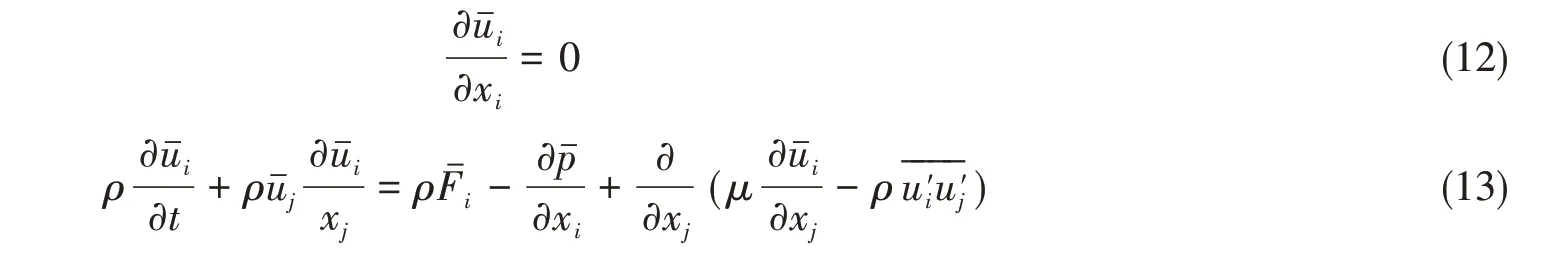
根据Boussinesq假设,雷诺应力可表示为
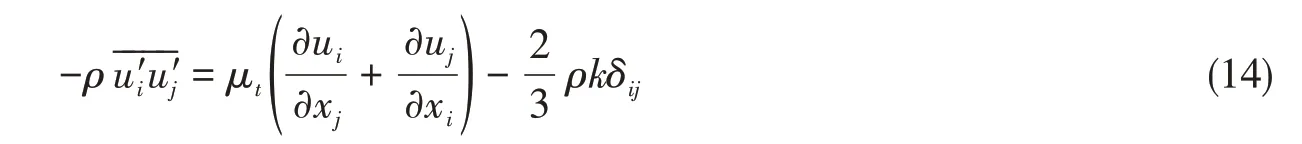
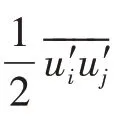
2.3 湍流模型
按作者及其他研究者经验,本文对于浮体上浮阻力CFD 计算采用RNGk-ε模型。针对位置水动力计算采用标准k-ε模型,旋转水动力计算采用SSTk-ε模型。
(1)RNGk-ε模型
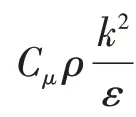


而Rε则可表示为

式中,η=Sk/ε,η0=4.38,β=0.012,常数ck=cε=1.393,C1=1.42,C2=1.68。
(2)SSTk-ω模型
在k-ω模型中将湍流涡粘度μt表示成湍流动能k和特殊湍流动能耗散率ω的函数:

a*为低湍流雷诺数修正系数,


Gk、Gω为湍流产生项,Yk、Yω为湍流耗散项,均考虑了低湍流雷诺数的修正。
k和ω分别满足方程(20)和方程(21):
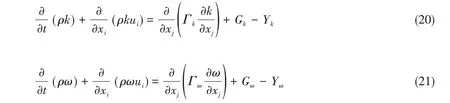
扩散系数Γk,Γω以下式定义:

式中,σk,σw分别为湍流动能k和湍流动能耗散率ω的普朗特数。速度及湍流耗散率ω以经验的形式给出:

式中,u+=u/uτ,y+=ρuτy/μ,uτ为剪切速度,κ=0.418 7,E=9.793。
(3)标准k-ω模型
湍流动能k方程为
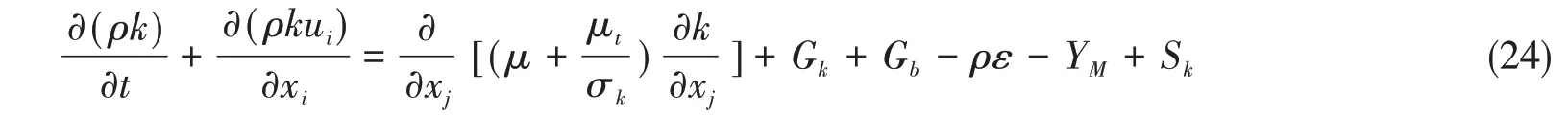
湍流耗散率ε方程为

式中,G1ε=1.44,C2ε=1.92,Gμ=0.09,σk=1.0,σε=1.3,Gk和Gb为湍流动能生成项,σk和σε为湍流普朗特数,Sk和Sε为源项。
2.4 离散格式及求解
对流项采用二阶迎风格式,扩散项采用中心差分格式,离散的流体运动方程求解采用单独求解器的求解方法,压力速度耦合问题以SIMPLE 法解决,离散方程以Gauss-Seidel 迭代方法求解,以代数多重网格技术加速迭代的收敛速度。
2.5 边界条件
(1)无穷远边界条件:在数值计算中以入口条件和出口条件描述。
入口条件:定义入口处的速度为无穷远处的速度,u=u∞;
出口条件:定义压力出口处的压力大小为无穷远处的压力值,p=p∞;
(2)物面条件:物面的速度为零,u→=0;
(3)对称面条件:在对称面处的法向速度为零,un=0,所有物理量在对称面法向上的梯度为零。
2.6 浮体上浮阻力预报
本文采用实尺度计算,以避免尺度效应。计算对象外形表面网格划分如图5所示,采用H-O型结构化网格。近壁面第一层网格内y+≈40,雷诺应力及湍流耗散标量的分布是以经验公式近似处理的。

图5 计算模型网格划分示意图Fig.5 Schematic diagram of computational model meshing
图6 给出了浮体表面压力系数分布图,图7 给出了阻力随速度的变化曲线。

图6 浮体表面压力系数分布Fig.6 Distribution of surface pressure coefficients of thebuoyant body
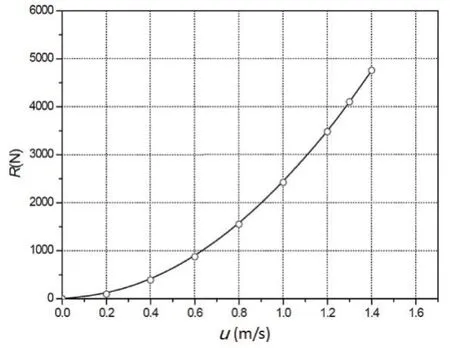
图7 浮体阻力计算结果Fig.7 Calculation results of resistance of the buoyant body
2.7 浮体位置导数及旋转导数预报
基于本文的数值计算方法,在图1 的xyz-G坐标系中xGz平面内,分别在攻角α=0°~9°,无量纲角速度q'=-0.15~0.15 范围内,计算浮体上浮受到的力矩M,对应的无量纲力矩系数M'= 2M/ρu2L3,其中ρ为流体介质质量密度,u为前方来流速度,L为浮体长度。它相对于α及q'的导数即力矩的位置导数和旋转导数M'w和M'q,其具体数值列于表2。图8 为α=1°条件下的浮体绕流流线图,图9为q'=0.1时浮体的瞬时流线图。

表2 水动力导数计算结果Tab.2 Calculation results of hydrodynamic derivatives

图8 浮体流线图(攻角1°)Fig.8 Streamline of the buoyant body at attack angle of 1°

图9 浮体旋转运动瞬时流线图Fig.9 Streamline of the buoyant body with rotating rate at certain instant
3 浮体上浮运动及稳定性判定
3.1 上浮极限速度计算
按1.2 节的上浮速度计算方法和图7 给出的阻力R(u),得到该浮体上浮极限速度为1.38 m/s,图10 给出了浮体的上浮速度与时间的关系曲线。
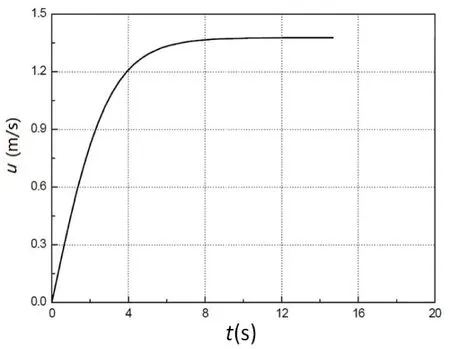
图10 上浮速度随时间变化曲线Fig.10 Buoying velocity versus time
3.2 浮体上浮姿态稳定性预估
前文1.1 节中判据式(7b)的物理本质是,若M'w>0,即浮体在有攻角时会产生发散力矩,则随着速度增加此力矩越来越大,而浮力产生的力矩为恢复力矩,大小与上浮速度无关,所以恢复力矩应在浮体任何速度下都大于发散力矩。因此上浮姿态稳定性判定仅需判断当浮体达到最大速度亦即极限速度时能否满足式(7b)判据。


4 浮体上浮水池试验验证
4.1 浮体上浮试验概况
为了对该全尺度浮体上浮运动的姿态稳定性结果进行试验验证,在中国船舶科学研究中心的水池内进行该浮体上浮试验。水池内装满淡水,浮体布置在位于水下一定深度的安装座上,安装座可调整初始姿态角。
浮体上浮试验时,正浮状态(零度倾角)试验的模型安装照片如图11所示,带倾角状态上浮试验的模型照片如图12 所示。试验过程中,通过水下相机拍摄浮体的上浮运动过程及姿态角变化,同时采用压力传感器记录浮体特定位置的压力变化,通过换算可获得浮体上浮过程的速度和位移随时间变化的曲线。

图11 试验模型(正浮)Fig.11 Test buoyant body model at vertical postion

图12 模型试验初始状态(倾斜上浮)Fig.12 Test buoyant body model at inclination postion
4.2 上浮极限速度验证
浮体匀速段上浮速度数值预报结果与试验结果进行了对比,如表3所示。由于水池内为淡水,对该淡水中的上浮试验结果进行了修正,修正为对应海水的上浮结果。从表3 中可以得到上浮匀速段的速度为1.33 m/s,计算值与试验值相比较为一致,相对偏差为3.8%。

表3 上浮极限速度计算与试验结果比较Tab.3 Comparison of floating velocity between numerical calculation and test results
4.3 上浮姿态稳定性验证
在水池中对该浮体进行了0°倾角和30°倾角全尺度上浮试验,通过在深度方向的水下高速摄像机拍摄浮体的运动姿态。上浮试验过程中的模型照片如图13所示,浮体上浮出水时的照片如图14所示。

图13 上浮模型试验Fig.13 Buoying of the body in the tank

图14 模型试验上浮出水Fig.14 Body floating to the surface
图15给出了浮体在30°初始倾角工况下,自23 m水深释放,浮体姿态角随不同深度变化的试验数据。从水池试验上浮运动的姿态角试验数据和上浮运动录像可以看出,该浮体在整个上浮运动过程姿态是稳定的。
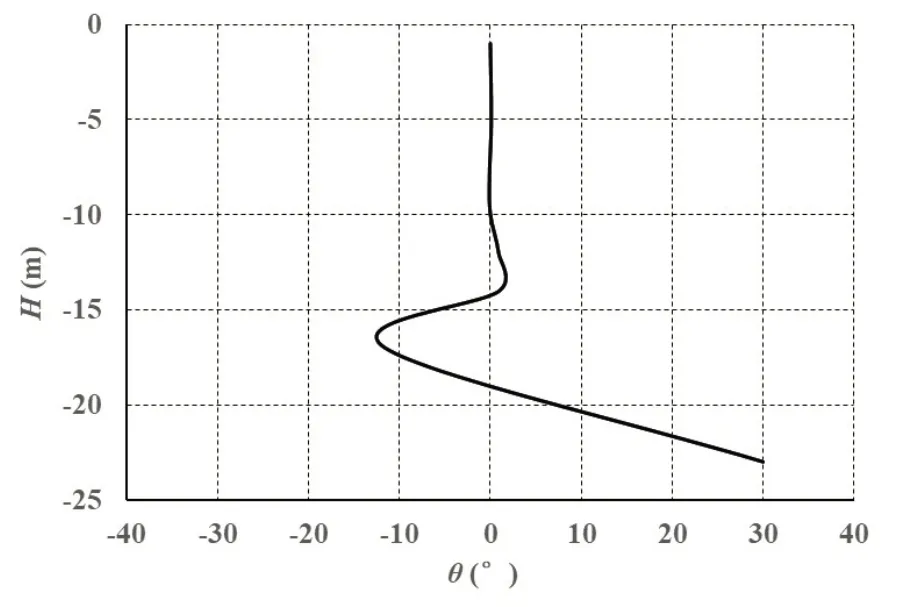
图15 上浮过程中不同深度下姿态角的试验结果Fig.15 Test results of attitude angle at different depths during buoying
5 结 论
对于实际应用浮体,工程上特别注重其上浮姿态的稳定性。本文的研究可得到以下结论:
(1)本文在小攻角状态下,对任意外形浮体进行了运动稳定性分析,并给出了姿态的稳定性判据。对大攻角情况,该判据至少应是稳定的必要条件。
(2)针对文中特定浮体,数值计算给出了阻力及力矩的位置导数与旋转导数,从而预报了该浮体的极限上浮速度,给出了姿态稳定的判断。
(3)理论预报结果得到了水池试验验证,表明本文提出的稳定性判据具有工程应用价值。

