微型抗滑桩-连梁组合结构抗滑机理试验研究
张院生 雷国平 杨伟鸿 马华 苏栋,3 吴泽雄 洪成雨,3
1.铁科院(深圳)研究设计院有限公司,广东 深圳 518063;2.深圳大学 土木与交通工程学院,广东 深圳 518061;3.深圳大学 未来地下城市研究院,广东 深圳 518061
微型抗滑桩造价低、施工快捷且对场地适应性较强,已成为边坡加固常用手段之一。与大直径抗滑桩在桩后形成土拱效应的抗滑机理不同,微型抗滑桩只能调动滑动面附近局部土体反力,产生相对较小的抗滑力,但往往进行多排布置并通过在桩顶设置连梁或顶板形成组合结构,整体上也具有较好的抗滑性能,可代替大直径抗滑桩用于边坡加固[1-3]。关于该组合结构的受力特性已进行了大量的模型试验和数值研究,主要集中在桩顶约束、临界嵌固长度、微型抗滑桩间距等方面[4-6]。微型抗滑桩-连梁组合结构的内力计算主要采用弹性地基梁K法或m法[7-11],没有考虑微型抗滑桩的受力变形协调。王金梅等[12]考虑了微型抗滑桩上各部分受力特点,将微型抗滑桩分成上部摩擦受拉段、中部滑坡推力作用段和下部锚固段进行分析,一定程度上反映了单桩的受力特性,但是没有考虑多排桩及桩顶约束的影响。以上方法仅限于弹性阶段的分析,没有考虑桩土的塑性破坏。对于微型抗滑桩极限承载力,主要通过假设桩土形成复合体,并在一定程度上考虑各桩受力的不均匀性,通过计算桩内加筋部分抗剪强度来分析结构的极限承载力[13]。此类方法比较符合以桩剪切破坏为主的岩质滑坡,而不适用于以弯曲破坏为主的土质边坡。
针对上述不足,本文展开模型试验,研究桩的塑性屈服过程以及该过程中组合结构的受力变化,进而揭示该结构的抗滑机理。
1 模型试验设计
1.1 模型箱与加载装置
设计可滑动的模型盒模拟边坡土体滑动过程中对微型抗滑桩的剪切作用。模型试验装置见图1。模型箱主体由上部可滑动箱和下部固定箱两部分构成,竖向高度分别为0.6、0.7 m,水平净长均为0.7 m,横向净宽均为0.4 m。模型箱正面采用20 mm 厚有机玻璃板,便于观察土样,其余部分均采用10 mm 厚铝合金板。采用水平油压千斤顶对上部箱体进行加载,使上部土体发生整体滑动。千斤顶最大行程150 mm,最大推力10 t,试验加载速率约为0.11 mm/s。千斤顶和模型箱之间安装一个量程为5 kN 的压力传感器,用于记录试验过程中的总推力。模型箱滑动的垂直方向架设有高清照相机(分辨率5 472 × 3 648),每10 s对模型侧边拍照一次,用于监测模型箱和桩顶的位移。
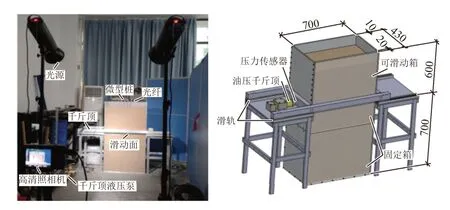
图1 模型试验装置(单位:mm)
1.2 模型桩
模型桩选用直径10 mm、壁厚1 mm 的铝合金管,主要物理参数见表1。微型抗滑桩外部沿桩长布设2 条OFDR 分布式光纤传感器,位于桩截面两侧,且放入模型箱时2 条光纤所在平面与土体滑动方向平行,用于监测微型抗滑桩沿滑动方向两侧的应变,进而分析桩内力变化。光纤通过丙烯酸酯胶固定在桩表面,且通过强力胶带进行保护,光纤粘贴完成后通过悬臂梁弯曲测试进行标定,并在弯曲测试中加载直至模型桩发生塑性变形,据此获取其屈服弯矩。光纤的测量精度为±1.0 × 10-6,采用静态测量时测点间距为10 mm,采用动态测量时测点间距为1.812 mm。桩顶连梁采用2个矩形铝合金条通过螺丝夹紧桩顶外露自由段的形式进行模拟,连梁尺寸为210 mm × 30 mm × 10 mm。

表1 模型桩主要物理参数
1.3 土体材料与建模
试验选用平潭砂,其平均粒径为0.41 mm,相对密度为2.662,最大、最小孔隙比分别为0.915、0.573,砂土相对密实度为45%。土样采用分层压实法制备,以保证其均匀性和可重复性。在土样制备前先将微型抗滑桩通过一道横梁固定在布设位置,然后每次称取相应的土样(约25.38 kg),通过漏斗和软管导入模型箱中,并平整压实至相应厚度(每层厚6 mm)。
1.4 模型试验参数
考虑微型抗滑桩结构的抗滑效果受到桩顶连梁和嵌固长度的影响,共进行4 次试验,包括1 次无桩试验和3次变参数试验,见表2。
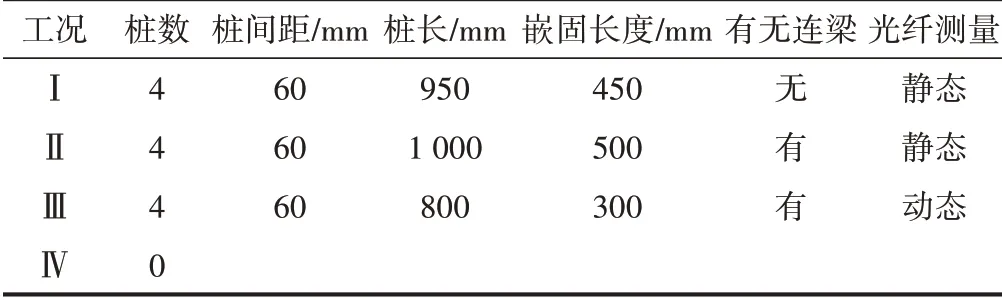
表2 试验参数
在垂直滑坡方向微型抗滑桩的响应区别不大,且当该方向微型抗滑桩的间距(横向间距)大于4~5 倍桩径时,排桩在土体水平运动作用下的响应接近于单桩[14],同时微型抗滑桩横向连梁的作用较小。故主要研究一列纵向微型抗滑桩在土体水平运动下的响应。微型抗滑桩的平面布设见图2,其纵向间距为6 倍桩径。根据土体滑动方向,桩A 相当于边坡加固中的后缘桩,桩D则为前缘桩。
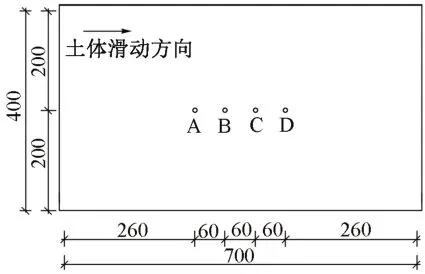
图2 微型抗滑桩平面布置(单位:mm)
2 试验结果及分析
2.1 桩顶位移
不同工况时桩顶位移见图3、图4。可知,试验过程中桩顶发生了明显的偏转和下沉;不同工况相同位置桩的桩顶位移相差不大,略大于土体水平位移。部分桩在初始阶段会出现微小上浮,但整体以轴向下沉为主,其中桩D 下沉量更大;在连梁的影响下,桩的轴向位移差异更大,连梁抑制了后缘桩的轴向位移而加大了前缘桩的轴向位移;在嵌固长度较小的情况下(工况Ⅲ),微型抗滑桩的轴向位移明显变小,且在加载初期出现更为明显的上浮位移,表明在该嵌固长度下桩的嵌固段有被拔出的趋势。

图3 工况Ⅱ时桩顶位移
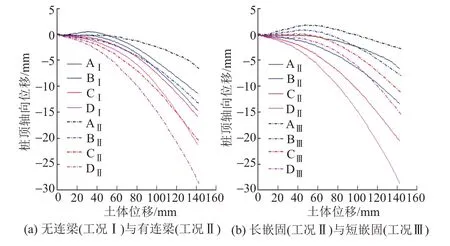
图4 不同工况时桩顶轴向位移
2.2 试验推力
千斤顶在试验过程中总推力见图5。可知:相较于工况Ⅳ,微型抗滑桩明显增加了滑动阻力;连梁提高了结构抗滑力(工况Ⅱ高于工况Ⅰ),而降低桩嵌固长度(工况Ⅲ)后,桩的抗滑力又相对降低了。
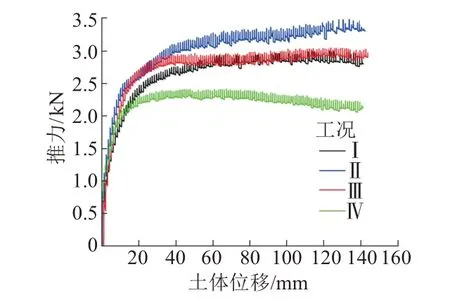
图5 千斤顶推力
2.3 微型抗滑桩内力
工况Ⅰ时桩CⅠ在不同土体位移下内力分布见图6。可知:随着土体位移的增大,桩的内力及土体横向反力均有所提高,桩土相互作用主要集中在滑动面附近一定范围内。桩在滑动面处的弯矩较小,即微型抗滑桩的抗滑以在滑动面处提供剪力为主。滑动面以上出现了与滑动面以下相反的弯矩,且二者在数值上处在相同的量级,有可能出现上下均发生桩体塑性应变的情况,这是微型抗滑桩与普通抗滑桩的主要区别之一。微型抗滑桩在滑动面处轴向受拉,在发生较大的偏转后也能贡献一部分抗滑作用。
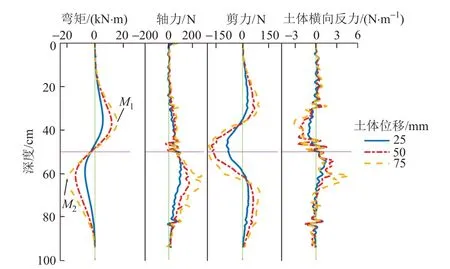
图6 工况Ⅰ时桩CⅠ内力和桩土相互作用力沿桩身的分布
根据滑动面上下弯矩峰值M1、M2和滑动面处剪力F的发展趋势,可将微型抗滑桩的内力发展分为弹性受力阶段(土体位移约40 mm 之前)和塑性屈服阶段。在弹性受力阶段,桩的内力随土体位移线性增加;而在塑性屈服阶段,桩的最大弯矩逐渐接近并超过屈服弯矩,同时滑动面处F(即抗滑力)达到相对稳定值,随土体位移变化不大。各试验中微型抗滑桩均发生了塑性屈服,见图7。
工况Ⅰ时桩内力随土体位移的变化见图8。
由图8(a)可知:最大绝对弯矩出现在滑动面以下,表明此试验中嵌固长度较长。前缘桩DⅠ在嵌固段的弯矩最大,并率先达到屈服弯矩,同时也导致该桩在滑体中的弯矩不再增加,所能提供的抗滑力(即在滑动面处的剪力)也开始降低。继桩DⅠ之后,CⅠ和BⅠ先后在嵌固段进入塑性阶段,但仍能继续调动滑体内的桩土相互作用,使滑动面以上桩的弯矩继续增加,桩的抗滑力持续缓慢增加。对于后缘桩AⅠ,其弯矩变化与桩DⅠ相反,即其在滑动段有达到屈服的趋势,而在嵌固段则没有。图8(a)中显示的弯矩超过屈服弯矩的情况与试验后对桩的观察一致(参见图7),桩BⅠ—DⅠ的嵌固段发生了明显的塑性变形,虽然M1也有达到屈服弯矩的情况,但还没有形成较大的塑性应变。

图7 微型抗滑桩塑性变形
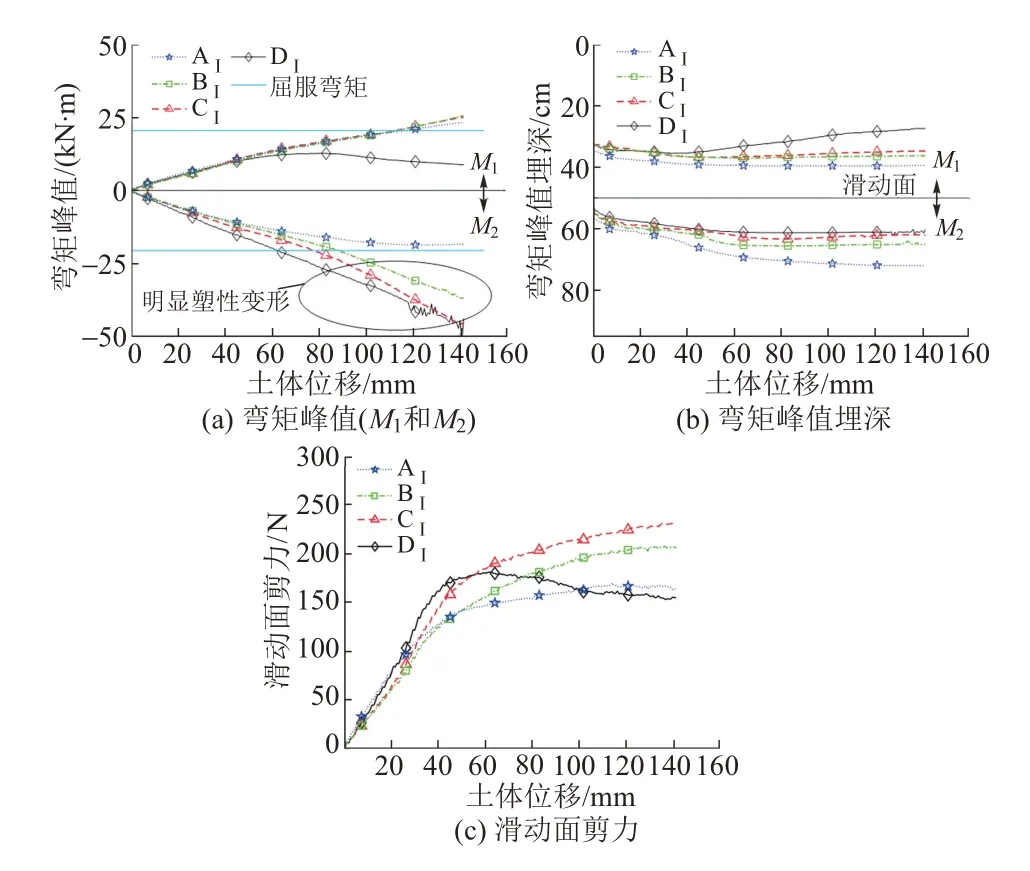
图8 工况Ⅰ时桩内力随土体位移变化
由图8(b)可知:越靠近前缘的桩(如DⅠ),其弯矩峰值的埋深越小,这在一定程度上反映了群桩效应对桩土相互作用的影响。一般地,桩的刚度相对土体越高,其最大弯矩位置与最大剪力位置之间的距离越大,据此可判断在滑动段中前缘桩DⅠ受到的土体反力水平更低,而嵌固段中则相反是AⅠ,群桩效应对边缘桩的影响更显著。同时,各桩弯矩峰值的埋深差异主要体现在塑性变形阶段。
由图8(c)可知:在弹性阶段边缘桩(AⅠ和DⅠ)提供的抗滑力高于中间桩(BⅠ和CⅠ),但整体上差别较小;在塑性阶段边缘桩的抗滑力明显低于中间桩,且前缘桩DⅠ抗滑力出现明显软化现象。
综上,多排微型抗滑桩的受力及破坏过程并不统一,有明显的渐进性破坏特征,且多排桩产生群桩效应使边缘桩更容易达到塑性变形,从极限分析的角度难以准确计算该结构整体的抗滑力。
2.4 连梁对桩内力的影响
工况Ⅱ时桩内力随土体位移的变化见图9。对比图8、图9 可知:工况Ⅱ、工况Ⅰ中桩的塑性屈服类似,但在连梁作用下,工况Ⅱ中DⅡ桩更早进入了塑性屈服,同时也带动AⅡ桩发生塑性变形,提高了抗滑力。相比于工况Ⅰ,工况Ⅱ中滑动段桩身也出现明显的塑性变形(桩AⅡ最为显著),边缘桩AⅡ和DⅡ分别在滑动段和嵌固段中弯矩最大,率先达到屈服破坏,而中间桩内力发展介于二者之间。
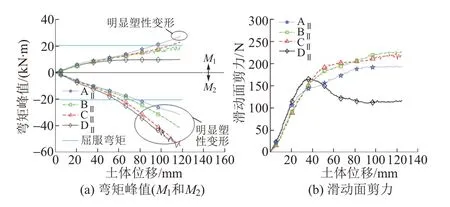
图9 工况Ⅱ时桩内力随土体位移变化
图8、图9土体位移30、100 mm时内力情况分别代表桩弹性和塑性阶段。经对比可知,弯矩峰值的位置受连梁影响不大。在弹性阶段,工况Ⅰ和工况Ⅱ弯矩较相近,但抗滑力已体现出较大差别,其中工况Ⅱ较高。在塑性阶段,工况Ⅱ弯矩M2明显高于工况Ⅰ,工况Ⅱ中后缘桩抗滑力仍较大,而前缘桩则相反,其原因与连梁对微型抗滑桩轴力的改变有关。
不同工况时土体位移40 mm、埋深10 cm 处桩轴力情况见图10。可知:对于没有连梁的工况Ⅰ,该处的轴力以受拉为主;而工况Ⅱ,连梁明显加大了后缘桩的受拉并使前缘桩在桩顶附近受压,这与图4(a)中连梁对桩轴向位移的影响相符。连梁对轴力的改变会产生二次弯矩,进而影响微型抗滑桩的横向受力。

图10 土体位移40 mm时埋深10 cm处桩轴力(正值代表受拉)
连梁加大了后缘桩的受拉并使前缘桩受压,改善了微型抗滑桩群的受力,提高了其抗滑力,并且该提升作用在桩的弹性受力阶段即已发生。
2.5 嵌固长度对桩内力的影响
工况Ⅲ时桩内力随土体位移的变化见图11。对比图9、图11可知,工况Ⅲ中桩的塑性屈服与工况Ⅱ相反,由于桩的嵌固长度明显变短,此时桩的塑性破坏主要发生在滑动段中(即M1位置)。参见图7 可知,最严重的塑性变形出现在B、C桩位上,桩AⅢ塑性变形较小而桩DⅢ没有发生塑性变形。
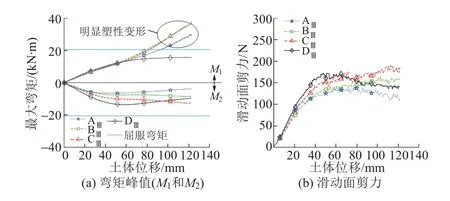
图11 工况Ⅲ中桩内力随土体位移变化
试验中嵌固长度的减小程度对弯矩峰值位置的影响不明显。在弹性阶段,嵌固长度的减小对弯矩影响不大,但已全面降低各桩的抗滑力。在塑性阶段,工况Ⅲ中M1要明显高于工况Ⅱ,而M2则明显低于工况Ⅱ,最终桩的抗滑力相对工况Ⅱ进一步降低了。
综上,相比于连梁对桩间受力的影响,过小的嵌固长度改变了桩的受力破坏模式,严重时更能使微型抗滑桩因被拔出而失效,参见图4(b)。然而,通过嵌固长度的优化设计可使M1和M2同时达到抗弯强度,充分发挥微型抗滑桩的抗弯性能。
3 结论与建议
1)微型抗滑桩桩顶水平位移与土体位移相近,且受连梁和嵌固长度影响不大。微型抗滑桩在桩顶以轴向下沉位移为主,连梁会加大右侧桩的下沉位移而抑制左侧桩,减小嵌固长度会减小桩顶的下沉。
2)桩顶连梁和足够的嵌固长度均能加大抗滑结构的承载力。微型抗滑桩在滑动面处弯矩较小,以提供抗剪力为主进行抗滑。滑动面上下分别有一个弯矩峰值,二者方向相反但数值上处在相同量级,即有两个可能出现桩体塑性弯曲破坏的位置。
3)受群桩效应影响,后缘桩和前缘桩分别在滑动段和嵌固段中弯矩最大,率先达到塑性屈服,而中间桩内力发展介于二者之间。在弹性阶段边缘桩的抗滑力要略高于中间桩,在塑性阶段则相反。多排微型抗滑桩的受力及破坏过程并不统一,有明显的渐进性破坏特征。连梁加大了后缘桩的受拉并使前缘桩桩顶附近受压,提高了其抗滑力。
4)后续可进一步通过数值研究,建立该结构破坏模式与各参数的定量关系,用于简化承载力的计算。由于结构破坏往往始于边缘桩,可考虑改进设计参数,通过改变排间距或加强该部位桩的屈服强度来提高整体结构的抗滑承载力。

