WinoNet: Reconfigurable look-up table-based Winograd accelerator for arbitrary precision convolutional neural network inference
Wang Chengcheng Li He Cao Yanpeng Song Changjun Yu Feng Tang Yongming
(School of Electronic Science and Engineering, Southeast University, Nanjing 210096, China)
Abstract:To solve the hardware deployment problem caused by the vast demanding computational complexity of convolutional layers and limited hardware resources for the hardware network inference, a look-up table (LUT)-based convolution architecture built on a field-programmable gate array using integer multipliers and addition trees is used. With the help of the Winograd algorithm, the optimization of convolution and multiplication is realized to reduce the computational complexity. The LUT-based operator is further optimized to construct a processing unit (PE). Simultaneously optimized storage streams improve memory access efficiency and solve bandwidth constraints. The data toggle rate is reduced to optimize power consumption. The experimental results show that the use of the Winograd algorithm to build basic processing units can significantly reduce the number of multipliers and achieve hardware deployment acceleration, while the time-division multiplexing of processing units improves resource utilization. Under this experimental condition, compared with the traditional convolution method, the architecture optimizes computing resources by 2.25 times and improves the peak throughput by 19.3 times. The LUT-based Winograd accelerator can effectively solve the deployment problem caused by limited hardware resources.
Key words:quantized neural networks; look-up table (LUT)-based multiplier; Winograd algorithm; arbitrary precision
Field-programmable gate arrays (FPGAs) have emerged as one of the promising hardware platforms for accelerating convolutional neural network (CNN) inferences due to the prominent advantages in terms of power consumption and acceleration performance versus current GPU- and CPU-based counterparts. Small-size filters, such as 3×3 kernels, provide an efficient way to store model weights in memory, thereby leading to data transfer speedups[1]. Data compression is used to lighten the throughput of CNN models. However, the accuracy of network inferences using low-precision quantization processing can be severely diminished and exceeds the acceptable threshold. As a standard user case, 8-bit quantization can already approximate the accuracy of the original network, and the quantization error can be ignored[2].
Efficiency-oriented architectures with small filters are adopted to reduce computation complexity. Most of the computation time is spent on a convolutional layer with 3×3 and 1×1 kernels. The consistency of the kernel types in different layers makes it possible to reuse operational units.
A popular way for hardware structure optimization is to parallel the multiply-accumulate (MAC) operations. Digital signal processing (DSP) blocks on FPGAs enable full-precision floating arithmetic operations to design parallel MAC operations. The parallelism degree depends on the amount of DSP resources. As DSP resources are critical to FPGAs, they are underemployed in the implementation of quantized neural networks (QNNs) working for customized low-precision inferences. Using other logical resources to build processing elements (PEs) to replace DSP blocks in a low-word-size design is necessary.
Different from LUTNet[3]and Hardieck et al.’s work[4], which aim to gain a high resource utilization and reconfigurability of look-up table (LUT) resources, the Winograd algorithm is introduced to reduce multiplication, provide a hardware algorithm co-optimization solution to reduce the usage of LUT resources, and propose an efficient LUT-based QNN accelerator for arbitrary precision network inference, named WinoNet.
The LUT-based architecture, including the inner element-wise matrix multiplication (EWMM) kernel and outer Winograd convolution (WC) architecture, optimizes the intra- and inter-parallelism of the convolution. Area-efficient convolutional structures explore the area and latency tradeoffs through the optimal setting of Winograd. A reconfigurable cluster of PEs uses a multiplexer (MUX) to control the data flow and wire connection. Accordingly, this article proposes a reconfigurable LUT-based Winograd accelerator to solve the bottleneck problem of neural network deployment.
1 Method
The LUT-based architecture is proposed for the quantized CNN inference, namely, WinoNet. Compared with the previous work[5], the Wino PE cluster was proposed for time-division multiplexing of Wino PE and improvement of resource utilization, and the full network deployment was realized to prove the versatility of WinoNet. The key computation unit is an LUT-based EWMM.
From the perspective of arithmetic density in CNNs, matrix multiplication consumes the majority of computation resources.The Winograd algorithm is used to perform matrix multiplication. The Winograd-based EWMM consumes fewer numbers of multipliers than traditional EWMM. By exploring the tradeoff between the LUT utilization and throughput, the optimal parameters are deduced for the quantized WinoNet.
The area and memory tradeoffs are analyzed by exploring parallel inter-kernel EWMM architectures. The LUT-based WinoNet is used to complete the hardware deployment design of VGG16 to prove the versatility of WinoNet.
1.1 Overall design
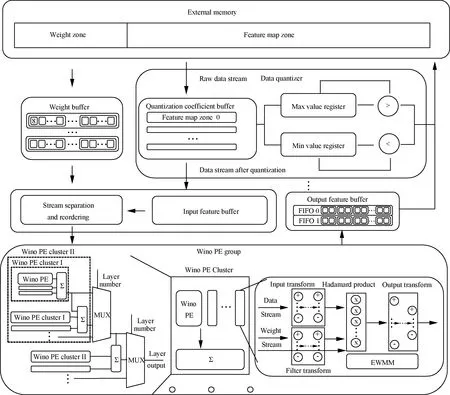
The network design consists of the memory interface, internal buffer, data quantizer, stream processing module, and Winograd PE (Wino PE) group, as shown in Fig.1. The external memory is used to store the weight parameters and intermediate feature map. The data from the weight buffer and input feature buffer are reordered by the stream processing module and sent to the Wino PE group to complete the operation. For the input feature map, a single row of pixels is stored in the BRAM, and four BRAMs are used to form the Winograd window to solve the bandwidth limitation. As the adjacent data calculation windows have two rows of data overlapping, only the bottom two rows of the feature map need to be updated from the DDR for the vertical window slide. The data read from the DDR is divided into two parts, which correspond to the two adjacent rows of the feature map. Accordingly, the calculation window required by the Winograd algorithm can be formed when the second row of data starts transferring. When the data load from the external memory to the on-chip memory is completed, the data read from the four BRAMs is reordered by the stream processing unit and converted into a single feature map and multi-channel form and sent to the Wino PE group, as shown in Fig.1(b).
The weight buffer caches the parameters corresponding to the input feature map calculation from the external memory. The data read from the weight buffer is divided into multi-channel filters by the stream processing unit and sent to the Wino PE group, as shown in Fig.1(c).
(a)
The Wino PE group is composed of multiple Wino PE clusters and the corresponding adder tree. The Wino PE cluster is used to complete the single-channel output feature map calculation.As the transform matrixes are constants, the transformation process is directly expanded in-to multi-level addition and subtraction to reduce resource consumption and timing pressure. The fixedness of the weight during the inference process allows for directly preprocessing the data and storing them in the external memory for use.
After the Wino PE group completes the calculation, the output data are stored in the output feature buffer and transferred to the external memory. The maximum and minimum values of the output data stream are obtained and stored for the calculation of quantization factors.
The innermost operation of the convolutional layer is the EWMM. The generic method to exploit DSPs makes the subsequent multiplication operation wait for the previous one, increasing the latency. In fact, each multiplication of the EWMM is independent of the other. The sum of product (SOP) method is adopted to flatten independent multipliers for each element-wise multiplication, and an adder tree is used to accumulate the multiplication results. Although more resources are consumed to implement calculations, the inner parallelism in EWMM can be effectively exposed, reducing the total delay. As the multiplier uses LUTs instead of relatively precious DSP resources, the additional resource consumption caused by the SOP is acceptable.
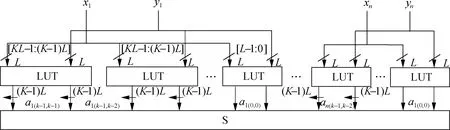
The LUT-based hardware structure is presented for the basic integer multiplication unit using the KCM approach, as shown in Fig.2. The multiplierxand multiplicandyare decomposed into several small parts with m-bits, wheremfits in the input of the LUT resource. Furthermore, these parts can be easily multiplied together through partial multiplication computation using LUTs. The multiplication order of each part is matched according to the multiplication distribution law[6].
(a)
1.2 EWMM kernel design
To reduce the circuitry consumption, the generalized parallel counter technique is used to design an efficient LUT-based adder tree. The LUT resources are fully used, and the carry chain structure is optimized in modern FPGAs.
1.3 WC optimization
The Winograd minimal filtering algorithm is introduced to optimize the convolutional layer, which reduces the number of multipliers used in the EWMM kernel. Although the Winograd algorithms have been used to accelerate CNNs, the implementations are dependent on DSP resources with full-precision matrix multiplication. WinoNet is the first custom-precision CNN inference that employs FPGA soft logic (i.e., LUTs) to implement efficient Winograd-based matrix multipliers. WinoNet can reduce the computation cost and overall latency. The internal calculation delay is only related to the multiplication operation.
1.4 Wino PE cluster design
The Wino PE cluster is made up of Wino PEs and the corresponding accumulator, as shown in Fig.1. The number of input channels is not the same for all the layers, leading to a difference in the number of Wino PE. The independent Wino PE instantiation and controller deployment for each layer cause additional resource consumption. A MUX is used to realize the dynamic adder tree combination and improve the utilization rate of Wino PE. For the Wino PE Cluster Ⅰ, which is the smallest cluster, the number of accumulator fans is determined by the minimum input channel number of the single-layer network. The pipeline design solves the time convergence problem caused by the excessive fan. After the single-cluster calculation, the MUX is used to control the data flowing into the subsequent accumulator structure or directly as the single-layer output.
1.5 Data quantizer design
Quantization refers to the process of reducing the number of bits. The common process is to obtain the maximum valueDmaxand minimum valueDminof the source data and calculate the quantization factor. The quantization factor is used to ensure that the variables are mapped to the quantization interval without omission. The calculation formula of the quantization stepΔand biaszis as follows:
(1)
(2)
(3)
xQ=clip(0,Qmax-1,xint)+z
(4)

(5)
whereQmaxis the interval length.
In the quantification process, the original data are scaled by the step size, and bias is added to shift the whole interval to the quantization interval (0,Qmax-1) for truncation processing. During the inverse quantization process, the data are corrected by the bias and multiplied by the step size to obtain the original data. As the basic PE is constructed by the LUT, the system has low complexity and high reconfigurable ability, which satisfy the need for arbitrary precision.
2 Design Space Exploration
The Winograd algorithmF(m×m,r×r) has different acceleration effects for different output sizesmand filter sizesr. Specifically, the reduction of multiplications brought by WC is given by
(6)
whereMtandWtare the multiplication numbers of the traditional convolution and Winograd-based convolution, respectively. For example, for a 3×3 filter, whenm=2, the multiplication is reduced by 2.25 times, and whenm=6, the reduction is 5.06 times.
In principle, the largermis, the more multipliers can be avoided. However, asmgrows, more adders are used instead. With some choices ofm, the overhead introduced from such adders can be higher than the area and latency benefit. How to choosemis the key to an efficient implementation. An evaluation coefficientELUTis introduced to evaluate the performance improvement under different values ofm.ELUTnormalizes the throughput of a single LUT to evaluate the average performance. A higher value ofELUTrepresents a more efficient convolutional architecture. The number of LUTs is defined asU, which is characterized below:
U=U0+Utrans
(7)
whereU0denotes the number of LUTs used for multipliers in EWMM andUtransdenotes the number of LUTs used for other operations, including the LUT-based adder and constant multipliers in the transformation operation.
The input feature map with the size ofH×Wis divided inton×ntiles, wheren=m+r-1. When using a sliding-window operation, the stride s should ben-r+1, sos=min our WCs. Therefore, the total number of convolution operations in the whole feature map is as follows:
(8)
whereαdenotes the number of WCs. The data throughput generated by the convolution operation sliding in the entire feature map can be represented as
(9)
wherefmaxis the operation frequency on FPGAs andLis the delay of the Winograd operation expressed as cycle clocks per operation.Sin=(m+r-1)2andSfi=r2are the input tile size and filter size, respectively, andNbitis the data bit width used for quantization.
The left part of Eq.(9) indicates the maximum operations of WCs per second. Finally, the evaluation coefficientELUTis given by
(10)
3 Memory Requirement
3.1 Memory analysis
The Winograd algorithm also introduces an extra memory overhead when computing transformations. Compared to traditional convolutions, it requires more static memory on the chip to store the input and output transform matrices. For these filters, the static memory increases by (n/r)2. WC is more efficient in terms of the utilization of feature data. Although direct convolution (DC) and WC use the sliding-window method to traverse the entire feature map, Winograd takes a larger input tile of the feature map than that of the filter. WC has less memory duplication of feature maps than DC.
For DCs, the tile size isr×r, and the stride equals 1. Therefore, the overlap factor is characterized as
(11)
For WCs withF(m×m,r×r), the tile size isn×n, and the stride size isn-m=r-1. Therefore, the overlap factor is
(12)
Assuming that the filter’s stride is 1, the reduction ratio of the memory wasted is as follows:
(13)
3.2 Memory and dataflow co-optimization
To further increase the parallelism of the inter kernel, the dataflow is optimized during convolution because the memory overlap is a severe bottleneck on the feature map. Referring to the GPU-based convolutional optimization strategy, the image-to-column (im2col) operation is used to flatten the convolutional layer and convert the convolution operations into matrix multiplications. The im2col operation is employed to transform theN×Ninput feature map divided byn×nblocks into a dataflow matrix made up of column vectors. Afterwards, matrix multiplication is conducted on this reshaped feature map with the wino-EWMM kernel. Then, the multiplied matrix is inverted back with the col2im operation to obtain the final results.
3.3 Memory bandwidth optimization
The parameter loading process is divided into weight loading and feature map loading. The weight loading will be completed at the beginning, as shown by the W-1 stage in Fig.3. Each block represents the transformation process of two rows of data. The slashed area is the sequential buffer. After the weight loading is completed, the first two lines of the feature map are cached from the DDR to BRAM (MRB-1). The data calculation could be started when the transferred data have constructed the calculation window. The interval between the start of the BRAM1xregion transmission (MRB-2) and the start of the Winograd calculation (DB-1) is recorded ast1. A time differencet2exists between the data cycle and memory read cycle.t2can be adjusted by various methods, such as changing the clock frequency. The data transformation from FIFO0 to DDR (MWB-1) can be performed when the Winograd calculation is started. As the memory bus may be occupied by the memory read logic at this time, there will be a memory wait (t3). The redundancy timet4at the end of MOB-1 is determined byt2. The idle time caused by the memory bus efficiency is recorded astD. The total timetmemoryfor the memory bus to complete a single-burst operation is
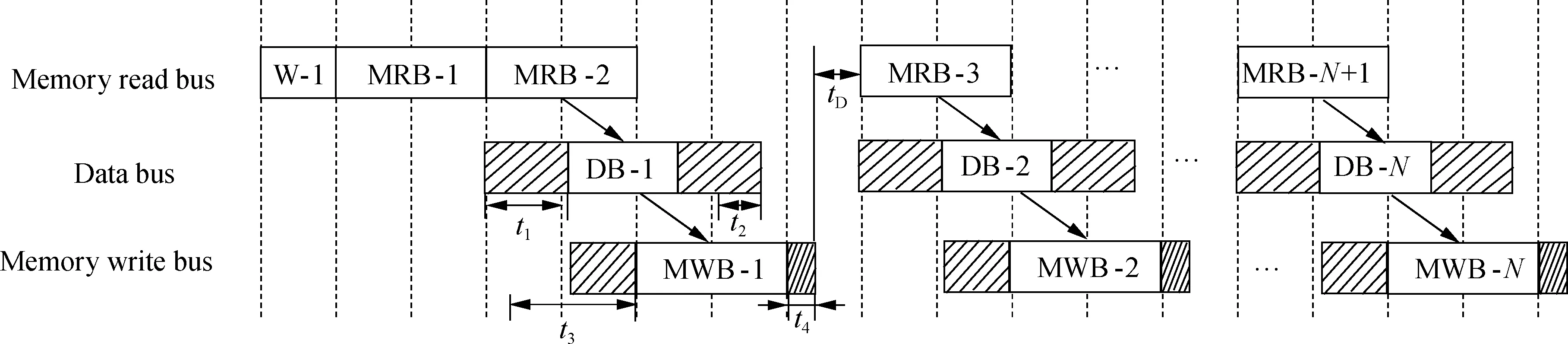
Fig.3 Timing diagram of the memory bus and data bus
tmemory=tMRB+tMWB+t4
(14)
wheretMRBandtMWBare the theoretical times to complete the data transformation. The data processing cycletdatashould be less than the memory burst cycletmemory.
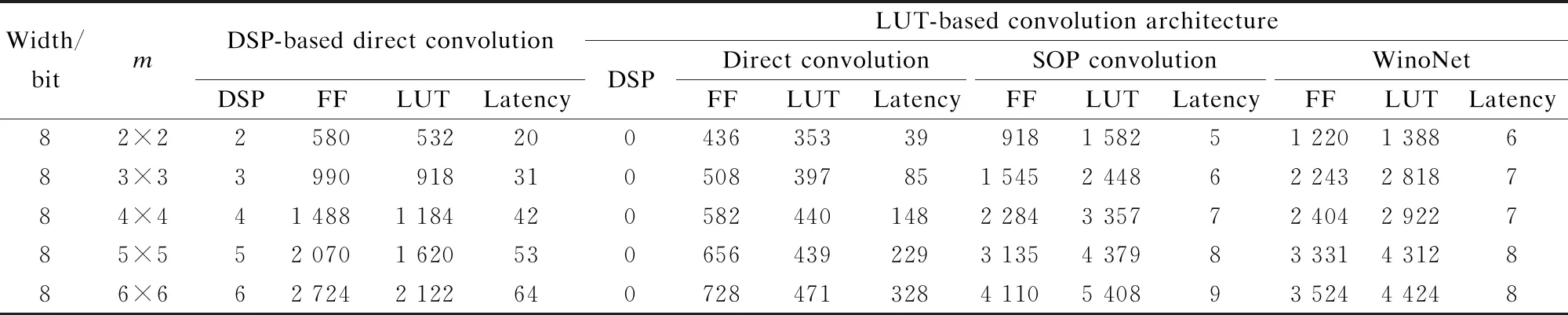
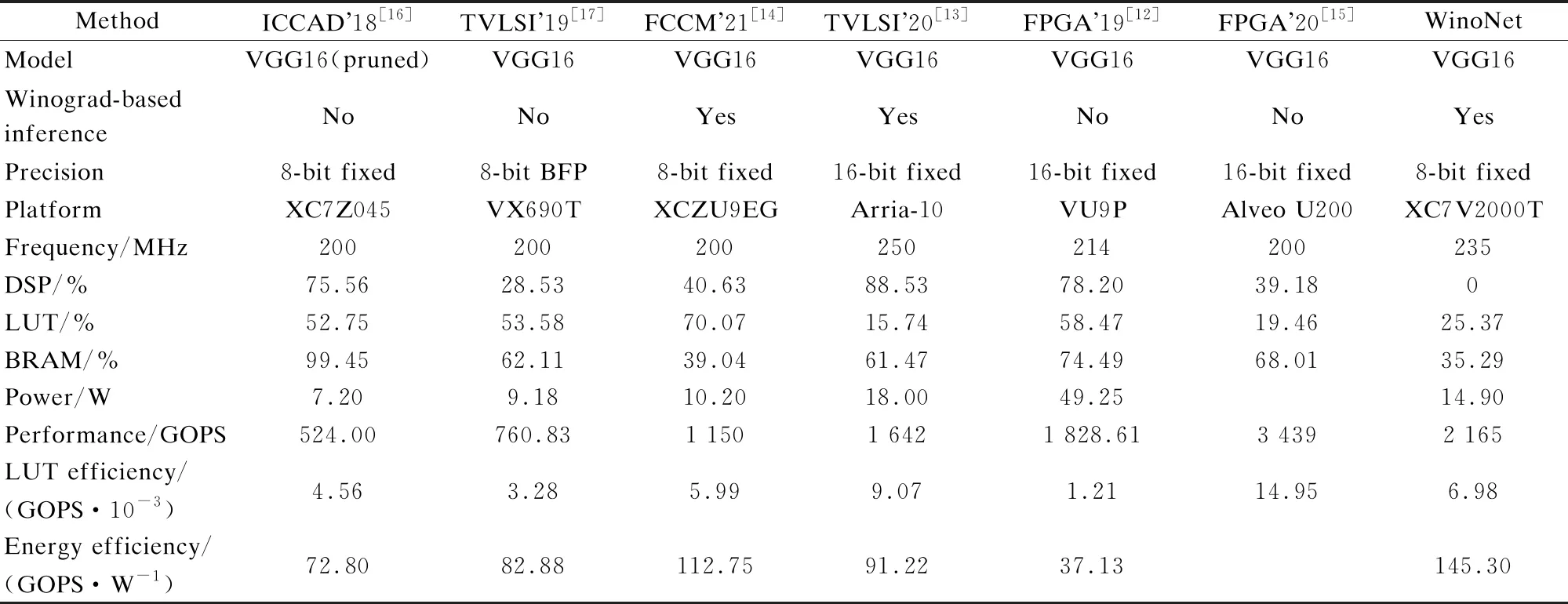
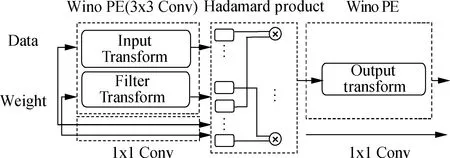
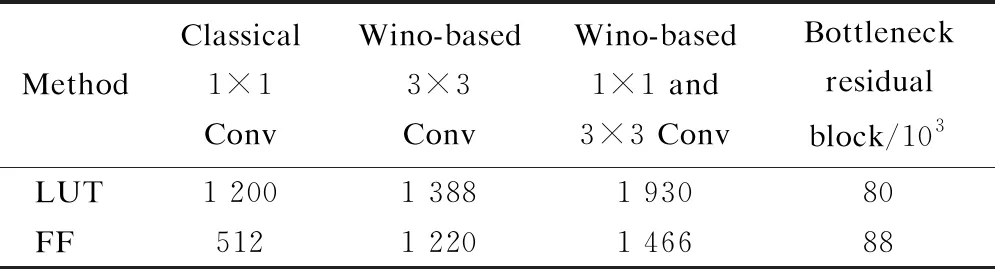
tdata=t1+tDB+t2 (15) The DDR bandwidth becomes the bottleneck rather than the calculated throughput when the parallelism degree is high. In this study, several experiments are conducted to investigate and validate the proposed architecture based on LUTs. Moreover, the implementation of the proposed method is evaluated on the Xilinx Virtex series FPGA platform. Xilinx Virtex XC7V2000T FPGA is used for prototyping CNN models. The LUT-based kernels are implemented on Xilinx Vivado 2019.2 in Verilog to facilitate efficient multiplication and compressor tree circuits. There are three comparison points:traditional convolution using DSPs[7-8], traditional convolution using LUT-based operators[4], and WinoNet. The proposed WinoNet is implemented with a 3×3 filter, i.e.,F(2×2, 3×3), which is the same size used in other implementations[8-11]. The intra- and inter-optimization architectures are implemented. The structures are tested with a variety of output sizes (m=2,3,4,5,6). The detailed experimental data are provided in Tab.1. Tab.1 Synthesis results of the resources and latency for the DSP- or LUT-based methods. The experiments are conducted in the same hardware configuration and corresponding logical resource usage. The direct implementation of the LUT-based convolution is conducted without any strategies. The other three implementations performed the row-unrolling operation for parallel acceleration. The SOP convolution additionally uses SOP for acceleration. The experimental results show that WinoNet has a great advantage in the inference speedup over traditional methods. Compared with the convolution structure based on DSPs, the proposed method can reduce the calculation latency by at least 3.3 times. The receptive field becomes wider, and the extra transformation consumes additional hardware resources. Compared with the SOP structure, WinoNet brings more resource consumption but does not reduce the latency when the output size is small. The advantages become obvious when the output size becomes larger. The area and speed tradeoff of the parameter selection ofmis critical. Regarding the different sizes of input tiles, the Winograd accelerators are evaluated usingELUTcoefficients, and the actual results are normalized to the (0,1) proportion. The experiments are conducted under feature map sizes (N), output sizes (m), and data bit widths (b) and are carried out on Xilinx Vivado HLS 2019.2. The value ofELUTchanging with the output size has a similar curve. Thus, only experimental data with a data width of 8 are shown in Tab.2. Tab.2 Synthesis results of the resources and latency for the Winograd-based methods with different F(m×m,3×3) When the output size becomes larger, the WC will greatly improve the speed performance by up to 19.3 times. The speedup factor represents the acceleration degree. Whenm=2,ELUTreaches the maximum value, but the speedup is only about one-third compared to the case ofm=6. The priority between performance and efficiency needs to be considered. In this study, settingm=2 is considered to be a balanced choice for the area and speed tradeoffs. The deployment in this study has instantiated 128 Wino PEs considering the external memory bandwidth limitation. The cluster scheduler is designed for the dynamic organization of the adder tree and wire connection. WinoNet is compared with several prior FPGA works, and power, resource estimation, and throughput are used as the metrics to evaluate the design. The throughput is defined as the operation amount (o) completed per unit of time and is measured in giga operations per second (GOPS). The calculation cycleTcalfor the output feature map is a quarter of the output feature map size. The formulas of the convolution operation amountoand throughputpare shown as follows: o=2Cink2HoutWoutCout (16) (17) wherefis the clock frequency;kis the kernel size;HoutandWoutare the output feature map size;CinandCoutare the input and output channel numbers. As power is related to multiple factors, such as resource consumption and clock frequency, energy efficiency and LUT efficiency are used as supplementary indices for comparison, as shown in Tab.3, and the measure is indicated in parentheses. Using only 25.4% LUTs and no DSPs, a frequency of 235 MHz, a peak throughput of 2 165 GOPS, and an average throughput of 1 928 GOPS are achieved. Tab.3 Implementation of FPGA and comparison with other works Compared with implementations using DSPs[12-16], energy efficiency has been demonstrated in WinoNet. WinoNet achieved up to 3.9 times more energy efficiency and 5.8 times more area reduction than Yepez et al.’s[12]. Compared with Winograd-based inferences[13-14], the WinoNet uses LUTs instead of DSPs for custom-precision computing and constructing more reusable architecture, achieving up to 1.6 times energy efficiency and 1.2 times area reduction. Compared with LUTNet, WinoNet provides a common architecture for arbitrary precision network inference. For CNN models, such as VGG16, with uniform-size convolutions, Wino PE can reduce resource occupation and power consumption. Many CNN models contain kernels of different sizes, such as MobileNet V2. Apart from the 3×3 convolutional layer, the bottleneck residual block is the main composition of MobileNet V2. 1×1 convolution mainly involves multiplication and accumulation. The internal structure of Wino PE is revised by adding a data bypass to directly transfer the data and weight to the Hadamard product module to support a general convolution of 1×1, as shown in Fig.4. Tab.4 shows the resource usage of the classical 16-channel 1×1 convolution, Wino-based convolution, and Wino-based bottleneck residual block in MobileNet V2. The bottleneck residual block transforms from 32 to 16 channels, with a stride of 1 and expansion factor of 1, and instantiates 32 Wino PEs. The modified Wino PE can process 16-channel 1×1 and regular 3×3 convolution kernels. Compared with separate 1×1 and 3×3 convolutions, the modified Wino PE achieved up to 1.34 times LUT reduction and 1.18 times FF reduction. The changes in kernel sizes and strides lead to the adjustment of the sampling window and transform matrix, and the adder tree mapped by the transform matrixes needs to be redesigned. The dilation rate also affects the sparsity of the algorithm, read/write flow of the memory system, and data ordering. The hardware architecture needs some adjustments to accommodate different algorithms. Further architecture needs to support dynamic window adjustment and data reordering to realize a general convolution. Fig.4 Internal structure of the modified Wino PE Tab.4 Resource usage comparison between different methods 1) The WinoNet enables a low-bit-width quantized neural network deployment optimization with its parallel EWMM kernel. The Winograd algorithm optimizes multiplier numbers to achieve convolution acceleration. 2) The LUT-based Wino PE optimizes the minimum PE, and the dynamic cluster reconfiguration improves resource utilization to optimize LUT efficiency. 3) The optimized storage format and memory access reduce data flipping, improve single data burst utilization, and further improve throughput. 4) Experimental results demonstrate that compared with the traditional convolution method,WinoNet achieves 2.25 times the calculation resource optimization and 19.3 times the peak throughput improvement.4 Experiment Results
4.1 Experimental setup
4.2 Hardware evaluation
4.3 Design space investigation

4.4 Performance comparison
4.5 Discussion
5 Conclusions
 Journal of Southeast University(English Edition)2022年4期
Journal of Southeast University(English Edition)2022年4期
- Journal of Southeast University(English Edition)的其它文章
- General Contents of Vol.38, 2022
- Roughness evaluation of three-dimensional asphalt pavement based on two-dimensional power spectral density
- Manufacturers’ channel selections under the influence of the platform with big data analytics
- Robust SLAM localization method based on improved variational Bayesian filtering
- Deciding whether manufacturing firms share product links on owned social media considering fan effects
- Damage identification of steel truss bridges based on deep belief network
