双锥-线栅型水平极化天线辐射特性研究

王皓琰, 李俊娜, 龚渝涵, 陈旭良, 崔光曦, 李兴文

(西安交通大学 电气工程学院, 西安 710049)

为研究电子系统及其组成单元的电磁脉冲(electromagnetic pulse，EMP)效应，评估电子系统和电力设备在电磁脉冲环境下的生存能力，并对其进行抗电磁脉冲的防护和加固，须对EMP模拟器进行研究和研制[1-4]。按电场方向，EMP模拟器可分为水平极化模拟器[5]和垂直极化模拟器[6]；根据生成电磁脉冲环境的原理不同，EMP模拟器又可分为有界波模拟器[7-8]和辐射波模拟器[9]。其中，水平极化辐射波模拟器以双锥笼型结构为主，包括双锥水平笼型和双锥椭圆笼型2种结构[10]，文献[11]中介绍了法国CEG中心的水平极化偶极子天线(horizontally polarized dipole, HPD)和美国的快上升沿电磁脉冲模拟器(horizontally fast rise electromagnetic pulser, HFREMP)，并进一步分析了双锥笼型关键参数对辐射场的影响。

然而，双锥笼形结构天线中锥形天线向笼形天线过渡段引起的电流负反射会使辐射电场产生快速下降，从而削减脉冲宽度[11]，半高宽很难满足ICE-61000-2-9标准中的要求[12]。Bailey等[11]提出了一种双锥线栅组合型水平极化天线，并通过计算验证了该型天线能够改善半高宽，使波形更接近标准波形。但文献对于该型天线的设计及关键参数对辐射场的影响并未做深入分析。

本文在Bailey提出的双锥-线栅型水平极化天线的基础上，对扩展天线的线栅结构进行了调整，具有架设机动、调节灵活和改善半高宽的优点。分析了双锥形天线和扩展天线的特性阻抗和辐射特性，并利用CST MWS电磁仿真软件对天线的辐射场进行计算，分析了几个关键参数对天线辐射特性的影响。

1 双锥-线栅型水平极化天线

1.1 双锥-线栅型水平极化天线结构

图1为双锥-线栅型水平极化天线三视图和总体视图。天线由对称双锥和对称线栅组成，双锥天线底面边缘均匀连接线栅，线栅末端连接分布式电阻接地。图1中：α为双锥的半锥角；r为双锥底面半径；H为双锥中心距离地面高度；d为地面上两侧接地线栅之间的距离；w为单侧线栅的宽度；R为每侧接地电阻的总阻值；ε为大地相对介电常数,ε=10；σ为地面电导率,σ=0.01 S·m-2。每侧线栅都包含9束扩展天线，每束中的天线根线为n，每束扩展天线都从双锥底面逐渐汇聚到地面附近，连接一个接地电阻接地，每侧有9个接地点。

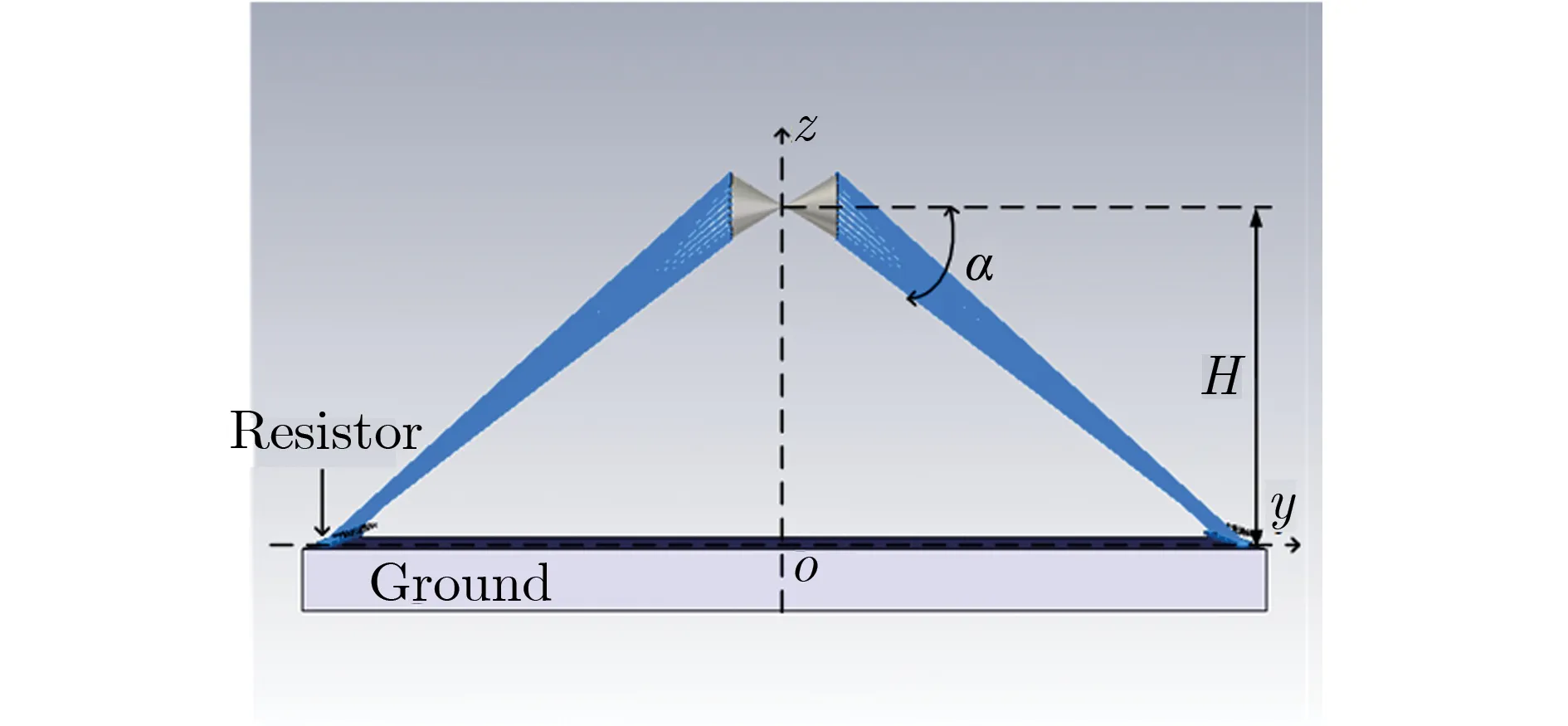
(a) Front view

(b) Top view

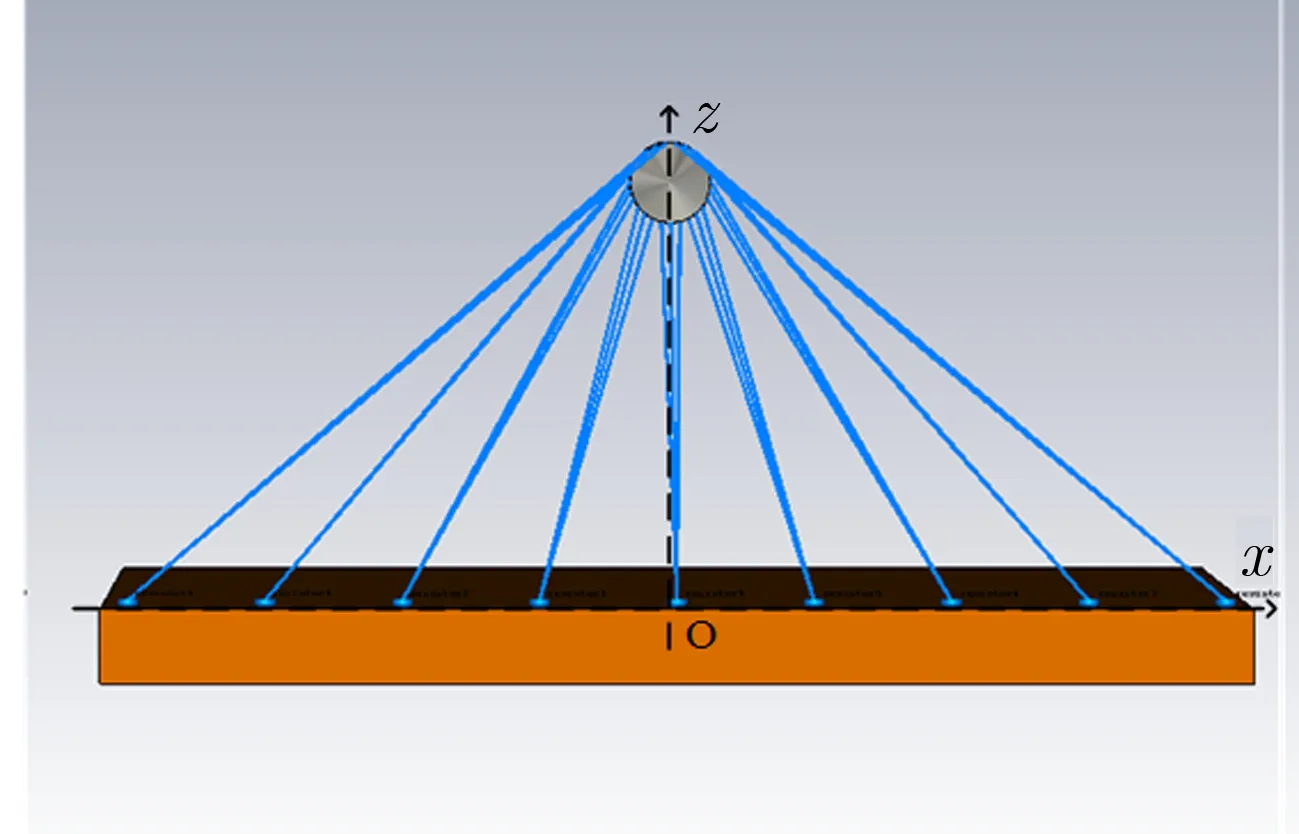
(c) Side view

(d) Overall view图1 水平极化天线结构图Fig.1 Configuration of the horizontally polarized antenna

天线由2种结构组成，需满足阻抗匹配条件，避免像双锥笼型天线一样在过渡段出现电流反射。填充扩展天线之间的空隙，就能达到圆锥曲线的效果，线栅可近似为锥型平板天线，其特性阻抗应和双锥天线的特性阻抗值相同，减小连接处电流反射。

理想双锥天线有严格的解析解[13]，锥型平板天线辐射场没有解析解，按照准静态近似，考虑边缘效应时，锥型平板天线的特征阻抗Zc可表示为[14]

(1)

其中：Z0为真空中的波阻抗；w′为锥板末端宽度；d′为两平板末端间距。

扩展天线虽然不是理想的锥型平板天线，但宽度w′和间距d′的设计可参考式(1)，保持天线的连续性，减少辐射场的畸变。同时，扩展天线的末端通过一定的阻抗连接到大地上，用于吸收扩展天线上的传播电流，减小由此造成的反射场。

1.2 天线仿真参数

本文采用电磁场仿真软件CST MWS进行仿真，该软件内置时域有限积分法等诸多算法，对不同的物理模型采用不同算法，求解准确，克服了传统 FDTD 算法在建模精度和场的描述方面的缺点[15-16]。

双锥半锥角取α= 32°，圆锥底面半径取r=1.5 m，双锥中心距离地面的高度取H=15 m，两个扩展天线极板之间的距离d=48 m,单侧极板宽度取w=64 m，单侧扩展天线根数为27根，单侧极板的总接地电阻值取双锥阻抗的1/2(R=75 Ω)。双锥中心的馈源采取电压峰值为2.5 MV，时间波形取前沿tr=2.0 ns，半高宽为28 ns的双指数波形。

仿真边界条件Zmin方向设置为“Electric(Et=0)”,其余均设置为完全吸收边界“Open(add space)”。考虑到天线结构和辐射场的对称关系，只需计算天线的1/4部分，将zox面设为电壁，yoz面设为磁壁，提高了仿真效率。根据最高频率fH=0.6/tr[17-18]来估算，仿真频率最高约为300 MHz，由于大地相对介电常数ε=10，所以大地中对应的最小波长λmin≈ 0. 316 m，这要求仿真空间剖分的网格Δ≤0. 031 6 m，将网格剖分设置为每波长15个网格。同时，锥天线和扩展天线的材料设置为“PEC”。

2 天线内辐射场分析

2.1 双锥半锥角对辐射场的影响

每侧取9束天线，每束天线取3根，仅改变半锥角的度数，则极板w宽度也随之改变。半锥角选取32°，36°，40° 3档，双锥输入阻抗分别为150，135 ，121 Ω，根据式(1)的计算，线栅极板w′/d′取值分别为1.33，1.59，1.89。在双锥形中心下方距地面3 m(0,0,3 m)，5m(0,0,5 m)处设置测点。不同半锥角下2个测点的水平电场波形如图2所示。

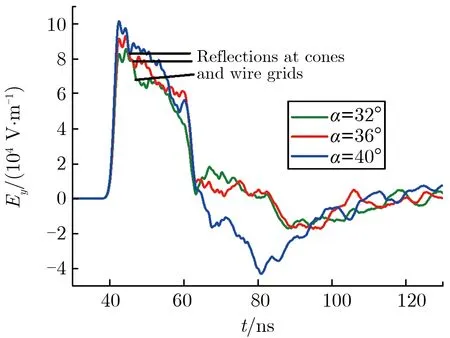
(a) Ey at point (0,0,3 m)

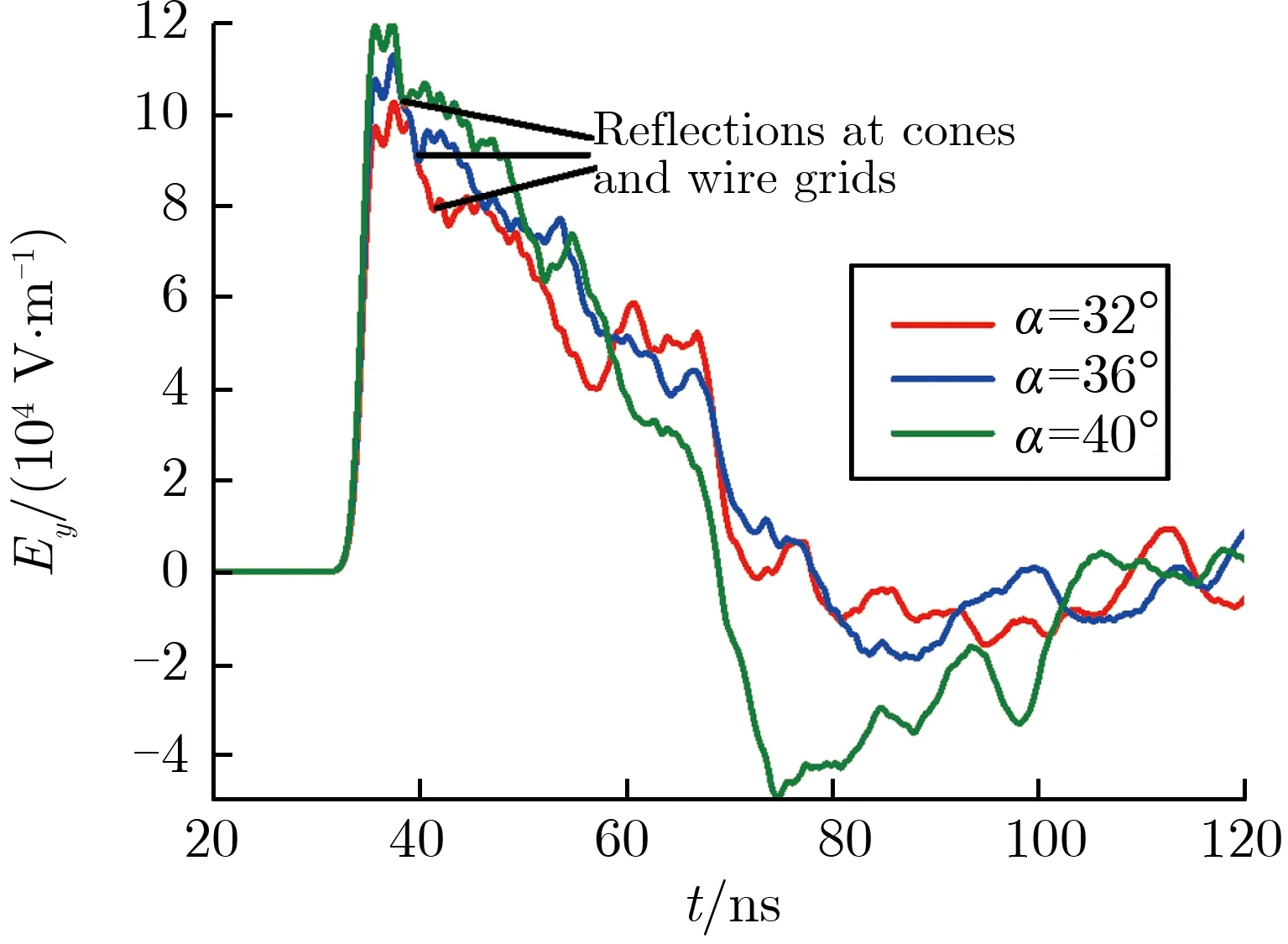
(b) Ey at point (0,0,5 m)图2 不同半锥角下2个测点的水平电场波形Fig.2 Horizontal electric field waveforms of two points under different α

由图2可见，同一位置的电场幅值随着半锥角的增加而增大。根据光程差的计算，锥和线栅连接处的反射均在波形到达峰值之后到来，该部分反射不会对幅值造成影响。

在底面半径不变的情况下，半锥角的增大会使场均匀性变差。半锥角不同时，地面上方5 m处的电场幅值分布如图3所示。由图3可见，在地面上方5 m，20 m×20 m范围内，半锥角为40°的辐射电场在靠近线栅的位置产生突变，原因在于半锥角的增加使两侧线栅的距离变短，离地高度相同时，辐射面积减小，考察的范围边缘更靠近线栅。线栅部分为非均匀金属板，线栅周围辐射场受单根导线的影响，使这些区域的电场产生了畸变。按平面上峰值的50%划定范围，当α=32°时，范围大于20 m×20 m；当α=36°时，y方向范围小于18 m；当α=40°时，y方向范围小于16 m。因此，为保证测试平面的均匀性，半锥角α应取32°。

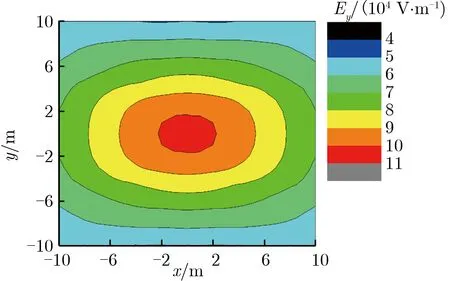
(a) α=32°

(b) α=36°

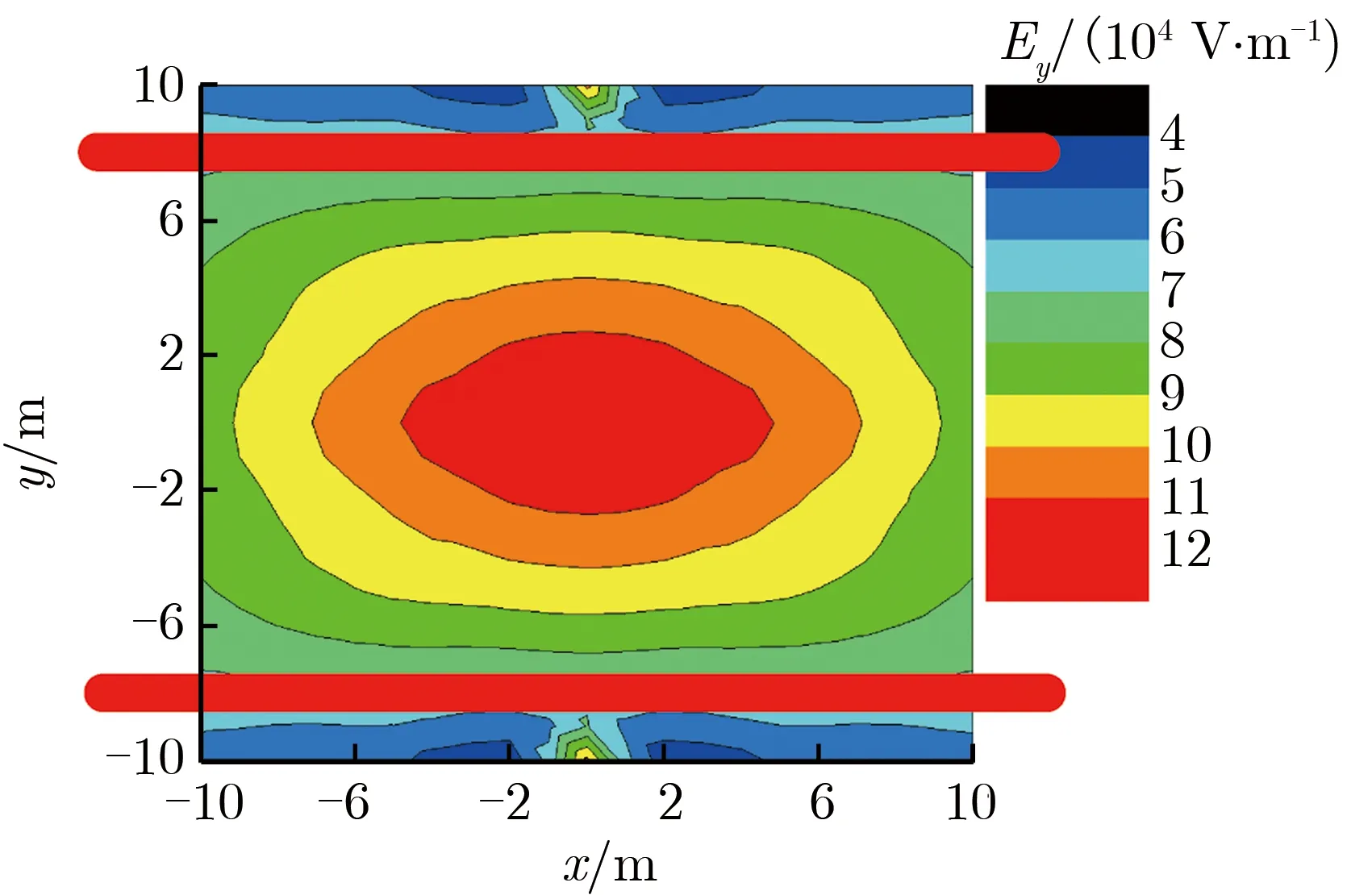
(c) α=40°图3 半锥角不同时，地面上方5 m处的电场强度幅值分布Fig.3 Distribution of Ey amplitude under different α at 5 m above the ground

同时，半锥角的增大也会增加工程难度，提高馈源电压可得到预期的电场强度，降低半锥角。因此，选择半锥角为32°能兼顾辐射强度和场均匀性。

2.2 锥底面半径对辐射场的影响

每侧取9束天线，每束天线取3根，分别取锥底面半径为1，1.25，1.5，1.75 m，其余参数不变，地面上方3 m处2个测点的水平电场波形如图4所示。由图4(a)可见，减小锥底面半径，电场幅值略有下降，双锥天线尺寸的降低，使双锥的辐射范围缩小。在双锥中心下方1.5 m之外的区域，来自双锥天线的高频能量降低，且扩展天线的特性对这些区域的辐射场影响较大，越接近地面，每束天线之间的间距越大，辐射强度降低，因此电场幅值会略有下降。在锥底面半径为1 m时，该测点峰值已受“锥与线栅连接处”的影响。由图4(b)可见，r=1 m时，峰值后的快速下降达到了25.5 kV·m-1，几乎达到了峰值的一半，采用此点判读则会大大降低半高宽的值，所以锥底面半径应大于等于1.5 m。

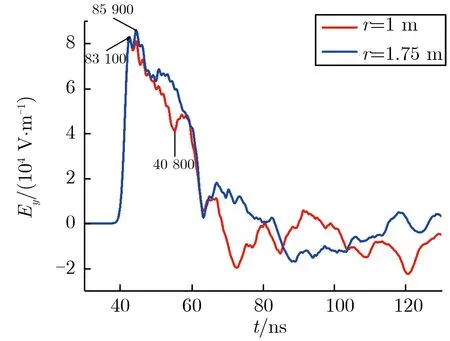
(a) Ey at point (0,0,3 m)

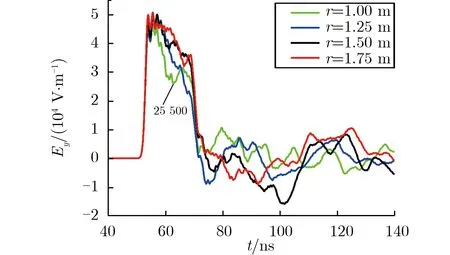
(b) Ey at point (0,10 m,3 m)图4 不同锥底面半径下2个测点的水平电场波形Fig.4 Horizontal electric field waveforms at two points under different radius

双锥和线栅连接处结构的不连续及相邻天线束之间的大间距，使与地面有一定距离测点的电场强度幅值均小于双锥天线辐射场公式的计算值。为保证一定区域内的辐射强度，双锥底面半径的选择不宜过小。双锥底面半径不同时，地面上方3 m处水平电场强度幅值分布，如图5所示。由图5可见，从中心位置开始，半径为1.5 m时的电场幅值就始终略大于半径为1 m时；半径为1.5 m时，电场强度大于50 kV·m-1的区域基本覆盖了20 m×20 m的范围，而半径为1 m时的区域覆盖范围只有18 m×20 m，所以，为保证辐射区域的电场强度，锥底面半径的尺寸至少应为1.5 m。

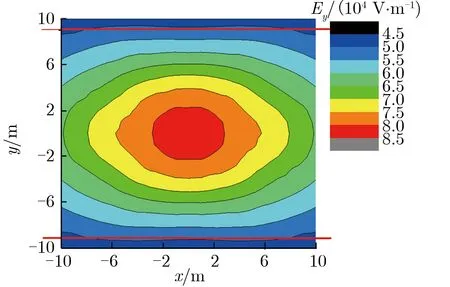
(a) r=1 m

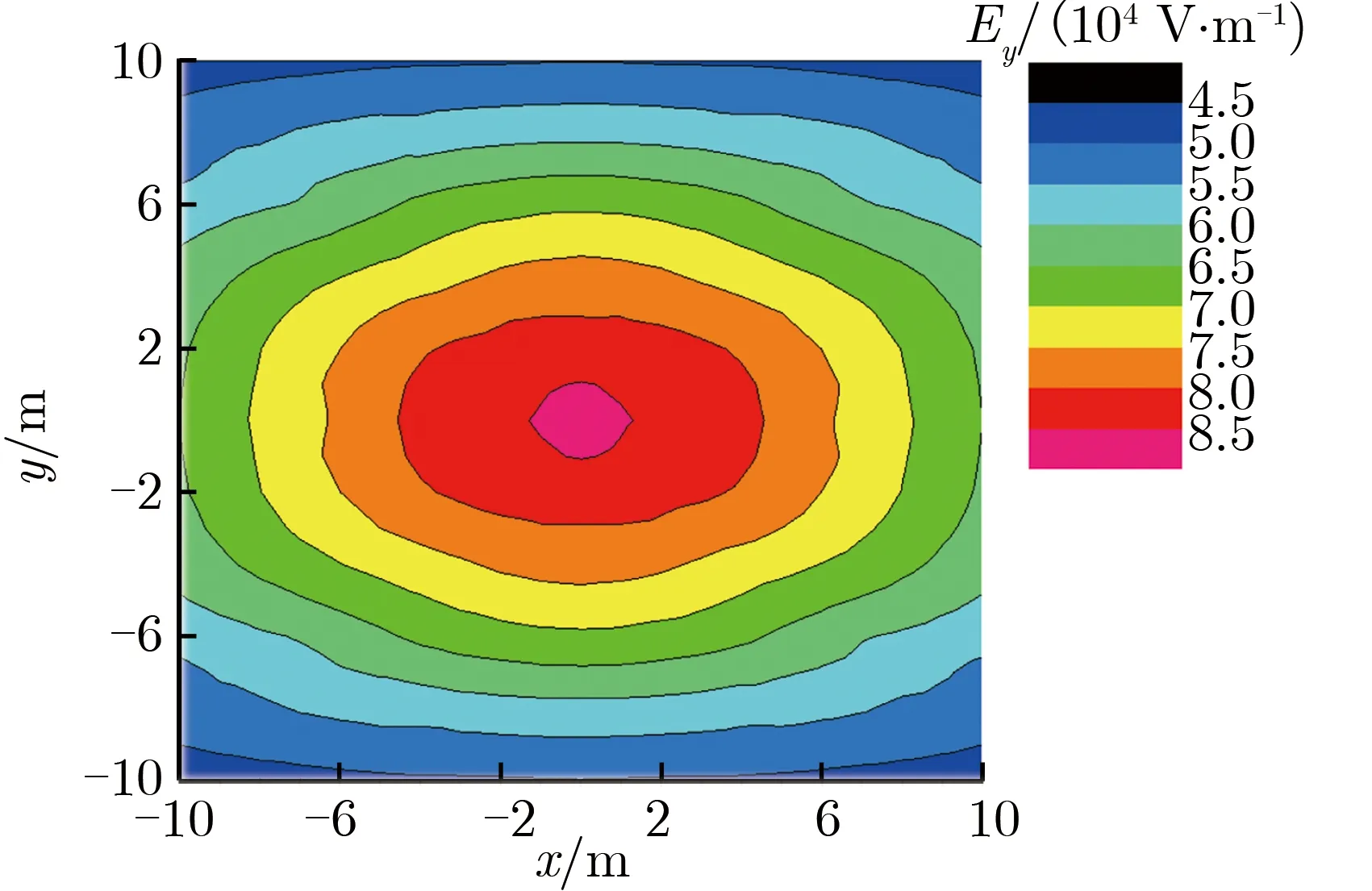
(b) r=1.5 m图5 双锥底面半径不同时，地面上方3 m处水平电场强度幅值分布Fig.5 Distribution of Ey amplitude under different radius at 3 m above the ground

然而，锥底面半径越大，双锥天线体积越大，制作难度也越大，耗材越多。在保证电场强度波形类似双指数波，且远场幅值不会降低过多的情况下，应尽可能缩小锥底面半径，所以锥底面半径选择为1.5 m是较理想的。

2.3 每束天线根数对辐射场的影响

每侧天线仍为9束，仅改变每一束天线的根数，每一束天线根数不同时，2个测点的水平电场波形如图6所示。由图6可见，改变每束天线的根数对上述2个测点水平电场的上升沿、幅值和半高宽均没有太大影响，但可能会影响测点处电场的时域波形。如，根数不同时，双锥正下方(0,0,3 m)的电场波形均下降平滑；而沿着x轴远离中心的位置的测点(16 m,0,3 m)处，根数过多，则会出现明显的“上扬”现象，导致波形出现第2个峰，且根数越多，“上扬”现象越严重。如，根数为3时，辐射场波形第2个峰的峰值为4.3×104V·m-1，而根数分别为5，8时，第2个峰的峰值分别为4.42×104，5×104V·m-1，达到第一个峰峰值的90%和98.8%。

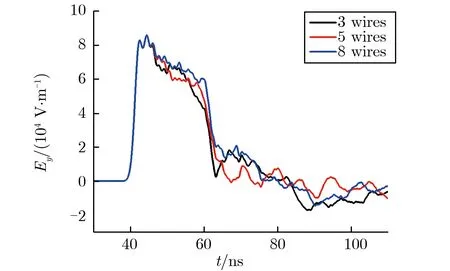
(a) Ey at point (0,0,3 m)

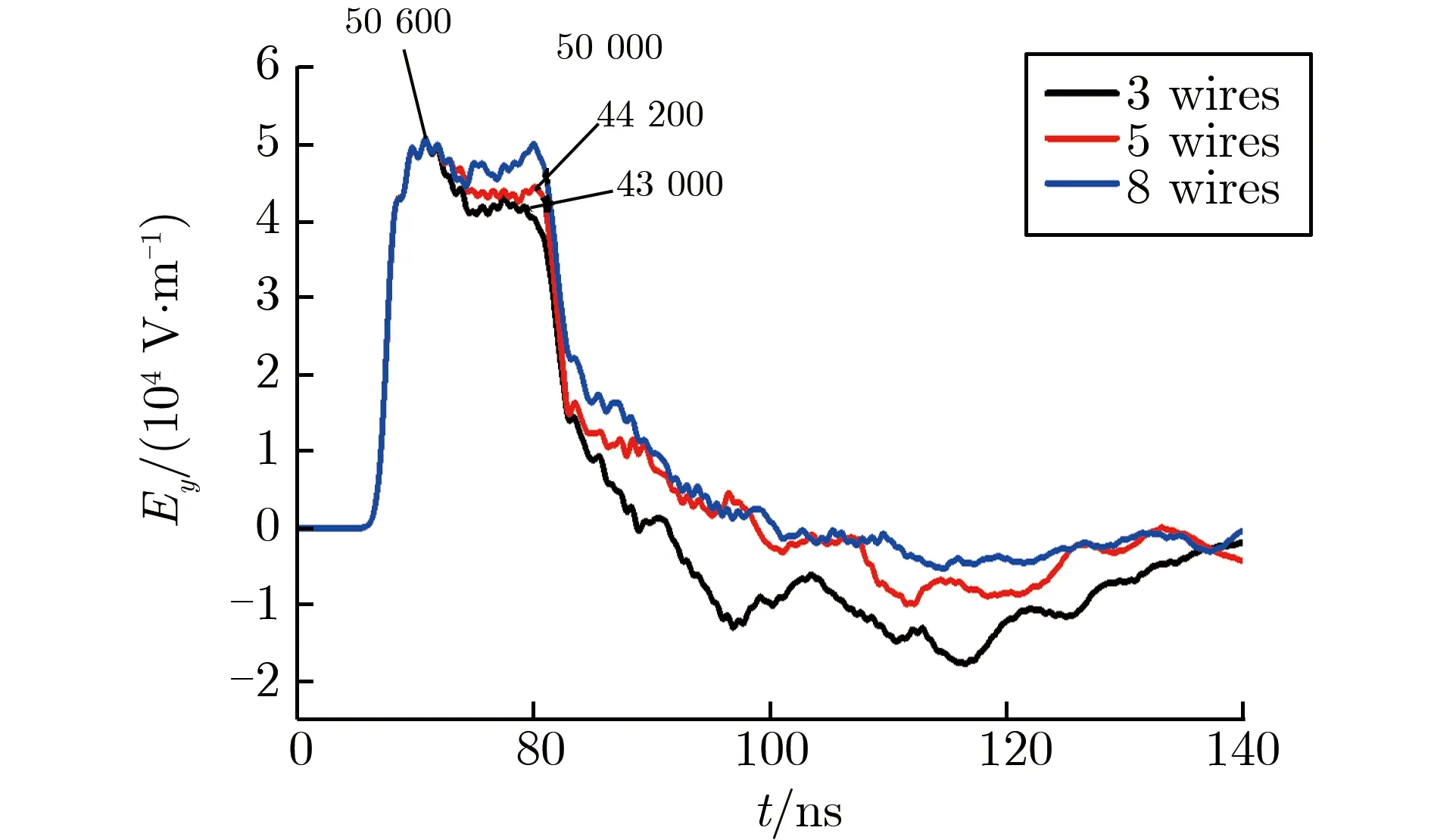
(b) Ey at point (16 m,0,3 m)图6 每一束天线根数不同时，2个测点的水平电场波形Fig.6 Horizontal electric field waveforms of two points under different numbers of wires

每束天线的天线根数不同时，不同测点水平电场波形的上升时间和半高宽如表1所列。

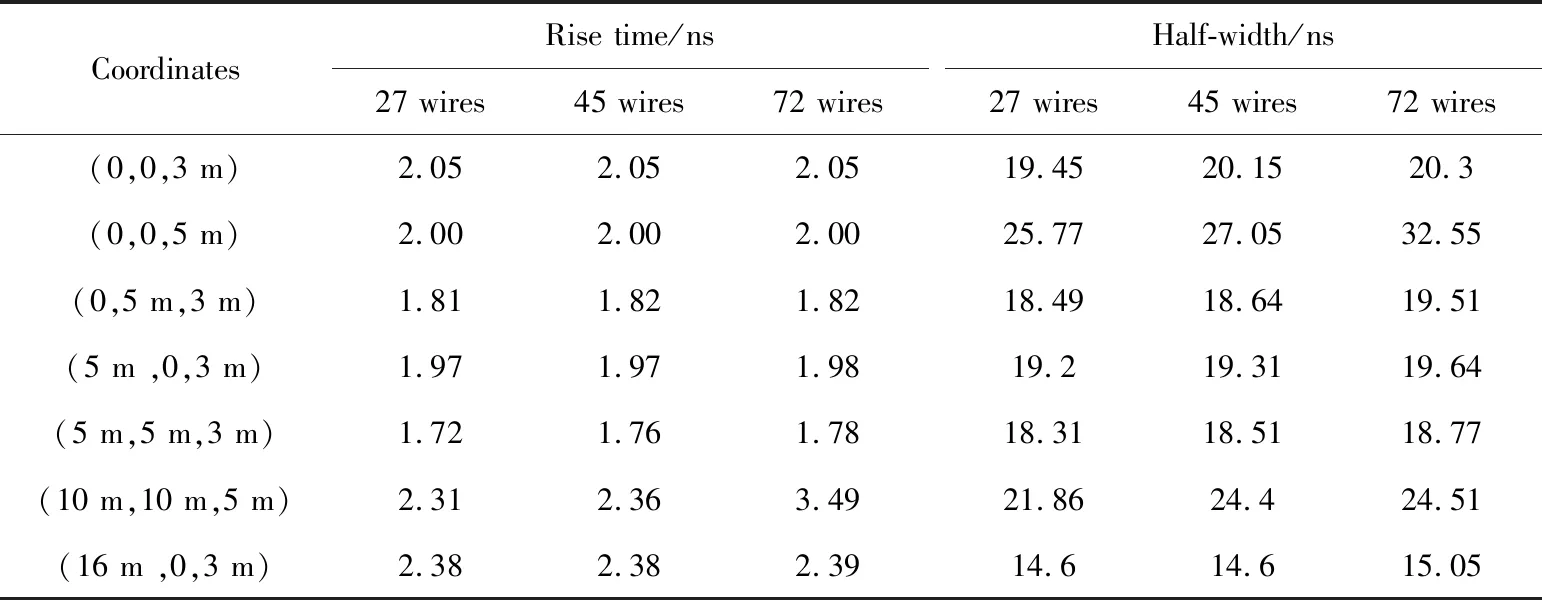
表1 每束天线的天线根数不同时，不同测点水平电场波形的上升时间和半高宽Tab.1 Rise time and half-width of horizontal electric field waveforms with different numbers of wire at different points

由表1可知，改变每束天线的天线根数对所选择的大部分测点场的上升沿的影响很小。其中，某些特殊位置，如测点(10 m,10 m,5 m)处，根数为72时，上升沿增加了51%，不符合要求。这是由于该测点更靠近线栅，“上扬”来得更早，叠加在波峰上，使幅值进一步增大，影响了上升沿的判读。增加每束天线的天线根数，会增加线栅天线的导波性能，使天线内传播的电磁波能量增加，导致同一测点场的半高宽增加。然而，对大部分区域来说，根数为8时，波形的半高宽比根数为3时提高了不到15%，效果并不明显。部分测点的上升沿略小于馈源的上升沿(2 ns)，一是因为在双锥正下方之外的区域受扩展天线影响大，且每束扩展天线之间有较大间距，辐射效果不如双锥天线，导致波形峰值无法达到理论计算值就开始下降，波形前沿也就随之缩短；二是因为某些测点的峰值受到“锥和线栅连接处”的影响，反射出现在上升沿，减小了峰值，降低了上升沿；三是因为测点距离地面过近，地面反射会降低峰值和上升沿。

天线根数的增加可提高输出电场的脉宽，但对大部分区域而言，并不明显，考虑地面反射的影响，实际上脉宽的提高更小。根数为8时，远场波形的上升沿甚至增加了50%以上，达不到IEC标准提出的技术指标[12]。天线根数增多也会增加架设难度和材料消耗，所以，从波形平滑度、脉宽、上升沿和工程实施角度来说，扩展天线每束天线的根数应为3～5。

2.4 架设系统对辐射场的影响

双锥-线栅型水平极化天线可使用吊车进行架设，以满足天线的机动，而吊车和横梁也会产生反射，但考虑到效应物一般置于地面附近，横梁和吊车距离过远，反射通常在地面反射之后到来，增加架设系统后的仿真波形主要特征不会发生变化，架设系统的影响很小。因此，新型水平极化天线的机动性并不会对辐射场产生不良影响。

3 结论

本文从特性阻抗角度对新型水平极化天线的反射进行分析，并从几个重要参数出发，对辐射场脉冲前沿、半高宽、幅值和场均匀性等多方面进行仿真计算和比较。研究结果表明：锥和线栅连接处存在一定反射，但线栅型扩展天线能很大程度延续双锥天线的辐射场；增大半锥角可提高电场幅值，但会使场均匀性变差，半锥角应为32°；增大锥底面半径可提高远场的幅值，过小的锥底面半径会使辐射场波形下降严重，锥底面半径应为1.5 m；增加扩展天线的根数，可稍增加半高宽，但根数过多增加了“上扬”趋势，对前沿、半高宽及幅值的改善很小，每束天线的根数应为3～5；架设系统因架设位置较远，对波形主要特征无影响。