脉冲功率装置中混合绝缘结构设计方法

赵 亮, 李 锐, 程 杰,2, 邱旭东,2,喻斌雄,3, 尚 蔚,2，高明珠

(1. 西北核技术研究所，西安 710024；2. 西安交通大学 电子物理与器件教育部重点实验室，西安 710049；3. 国防科技大学 前沿交叉学科学院，长沙 410072)

随着脉冲功率技术的蓬勃发展，如Z/ZR[1]，Saturn[2]，Magpie[3]，Angara-5-1[4]，PST[5]，Yang[6]，闪光二号[7-8]，强光一号[9-10]和FLTD[11]等一大批高电压、大电流加速器问世。同时，20世纪末至21世纪初，随着高功率微波(high power microwave, HPM)技术的迅猛发展，一大批纳秒、兆伏量级的重复频率加速器建成，包括俄罗斯的Sinus[12]和Radan[13]系列加速器，中国的TPG[14]、CKP[15]和CHP[16]系列加速器等。脉冲功率技术的发展，大大促进了高电压绝缘技术的发展。

从1960年开始，英国原子武器研究中心(Atomic Weapons Research Establishment，AWRE)的Martin等[17 -18]开展了大量短脉冲条件下的绝缘实验研究，并提出了一系列实用的击穿阈值公式。除此之外，俄罗斯托木斯克理工大学(Tomsk Polytechnic University，TPU)、美国北极星公司[19]、美国圣地亚国家实验室[20-21]、中国科学院电工研究所[22]、西安交通大学[23]和西北核技术研究所[24-27]等单位的研究人员也报道了大量与绝缘设计相关的公式。然而，这些公式关注的仅是某一类绝缘介质失效现象，尚未见一套完整的绝缘设计方法。因此，还需在绝缘设计方面进行研究和探索。鉴于此，本文总结并提出了脉冲功率装置中绝缘设计的方法，该方法的基本思想是对绝缘结构中涉及的失效形式进行通盘考虑。依据该方法设计的绝缘结构，在满足寿命指标的前提下不存在绝缘短板。

1 绝缘设计的基本思想

本文绝缘设计方法的基本思想有2点：一是将绝缘结构视为混合绝缘结构，通盘考虑其绝缘失效风险；二是从可靠度和寿命出发，在给定可靠度和寿命的前提下计算不同绝缘形式的许用电场。

1.1 3种基本混合绝缘结构的7种绝缘失效方式

高压电气设备中的绝缘结构可概括为固-气绝缘结构、固-液绝缘结构和固体-真空混合绝缘结构3种，这些结构主要起绝缘和支撑作用。除固体和界面外，液体、气体和真空可认为是流体，图1为3种基本混合绝缘结构的示意图。

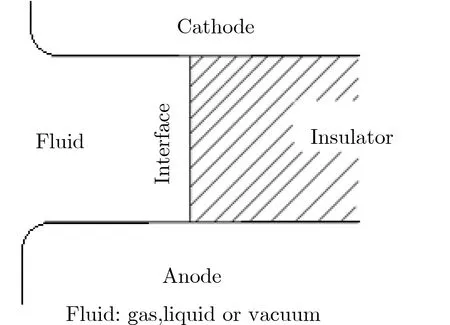
图1 3种基本混合绝缘结构的示意图Fig.1 Schematic diagram of three kinds of composite insulation structure

对于每种混合绝缘结构，绝缘失效可能由不同方式造成。如，对于固体-真空混合绝缘结构的绝缘失效方式可能是真空击穿和固体击穿，也可能是真空沿面闪络；固-液混合结构的绝缘方式除固体击穿外，还可能是液体击穿或固-液沿面闪络；固-气混合绝缘结构的绝缘失效方式除固体击穿外，还可能是气体击穿或固-气沿面闪络。所以，对脉冲功率装置而言，总共有固体击穿、液体击穿、气体击穿、真空击穿、固-气沿面闪络、固-液沿面闪络和固体-真空沿面闪络7种潜在绝缘失效形式。3种混合绝缘结构所对应的7种绝缘失效方式如表1所列。

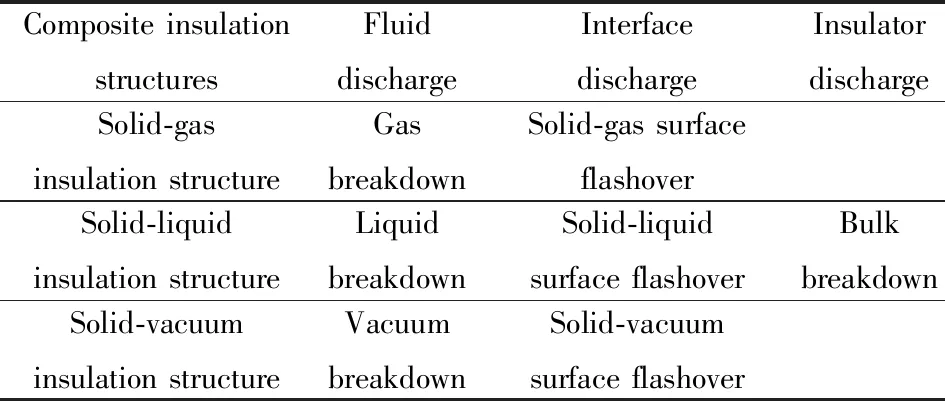
表1 3种混合绝缘结构对应的7种绝缘失效方式Tab.1 Seven failure patterns in three typical insulation structures

1.2 不同绝缘形式的可靠度

可靠度R定义为产品、零部件或系统维持一定功能的概率，是描述产品、零部件或系统可靠性的重要指标。R值越大，说明零部件的可靠性水平越高。脉冲功率装置中不同绝缘结构的可靠度主要受外施电场E影响，即：R=R(E)；同时也随时间或脉冲数变化，以脉冲数N为例，即：R=R(E,N)。一般情况下，外施电场越高，脉冲数越多，绝缘结构的可靠度越低。此外，机械应力、应用环境级材料品质等因素也能对可靠度产生影响[28]。需说明的是，本文给出的混合绝缘结构设计方法，认为上述因素固定，仅考虑电场和脉冲数对可靠度的影响。

传统设计认为，真空沿面闪络阈值提高，意味着混合结构整体绝缘性能会提高。然而，绝缘结构耐受一定脉冲数后，体击穿也可能发生，造成绝缘失效。这个现象可从可靠度角度进行解释：当脉冲功率装置运行足够多的脉冲数后，固体绝缘结构自身的可靠度将低于真空沿面的可靠度，使体击穿发生，造成绝缘失效。

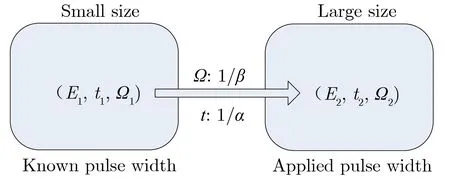
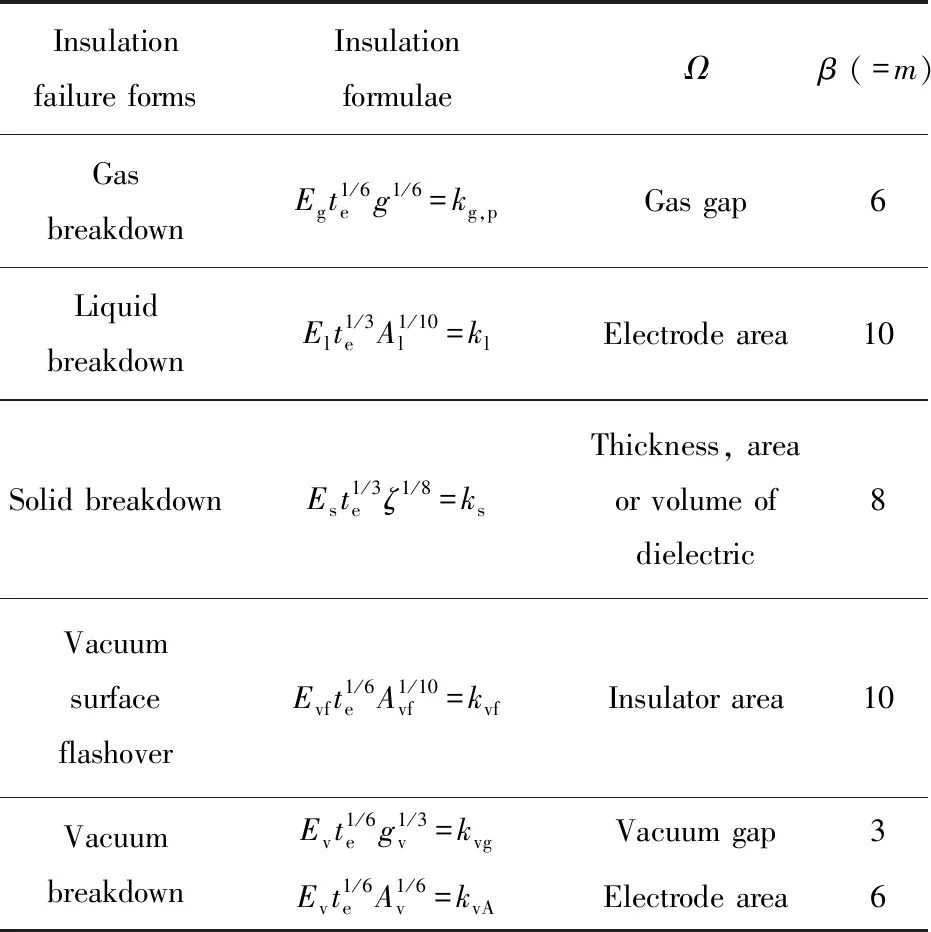
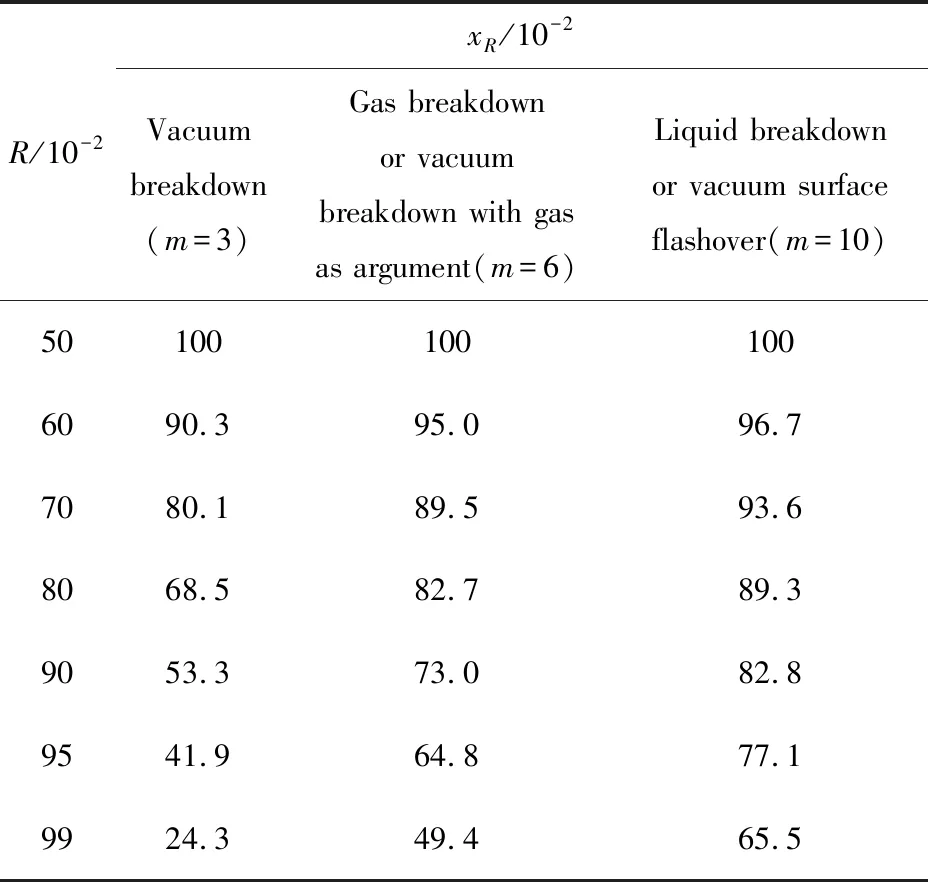
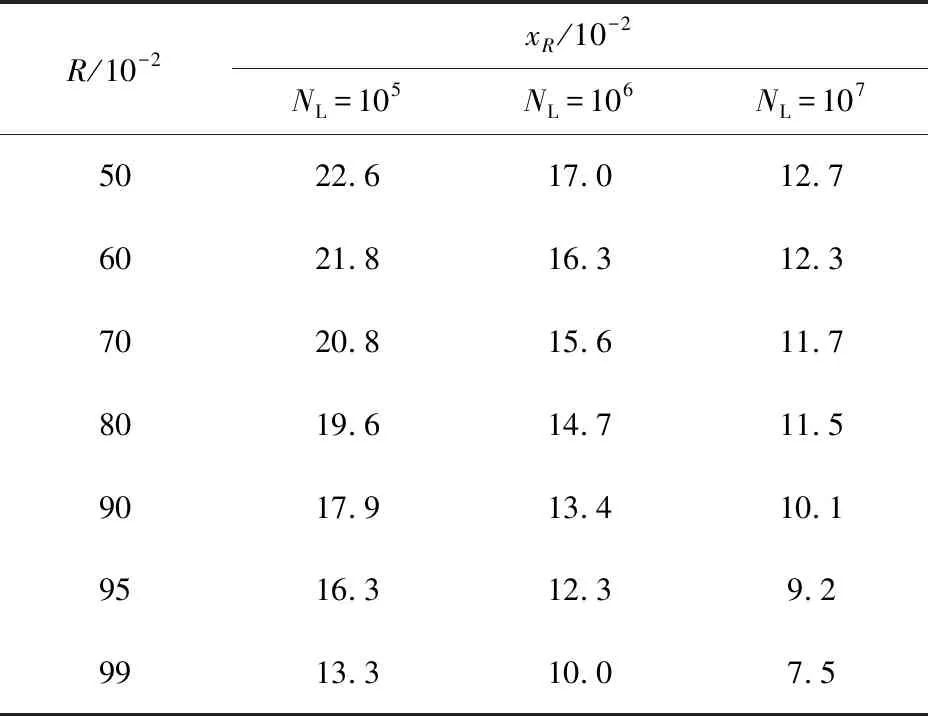
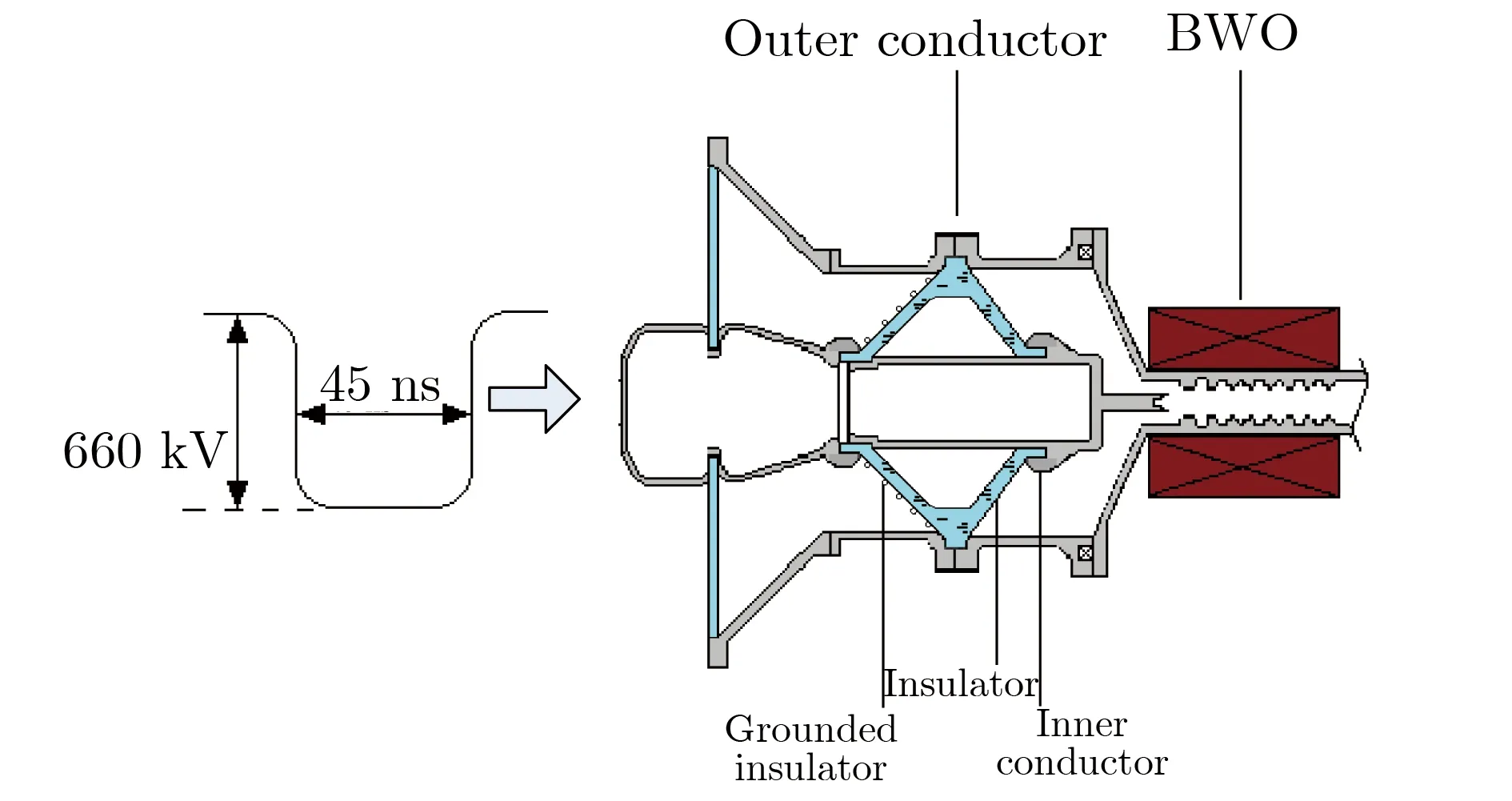
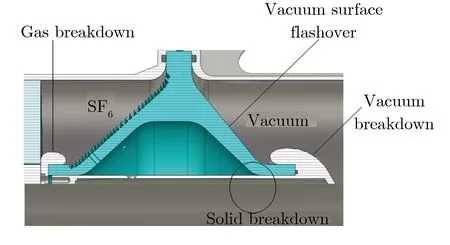
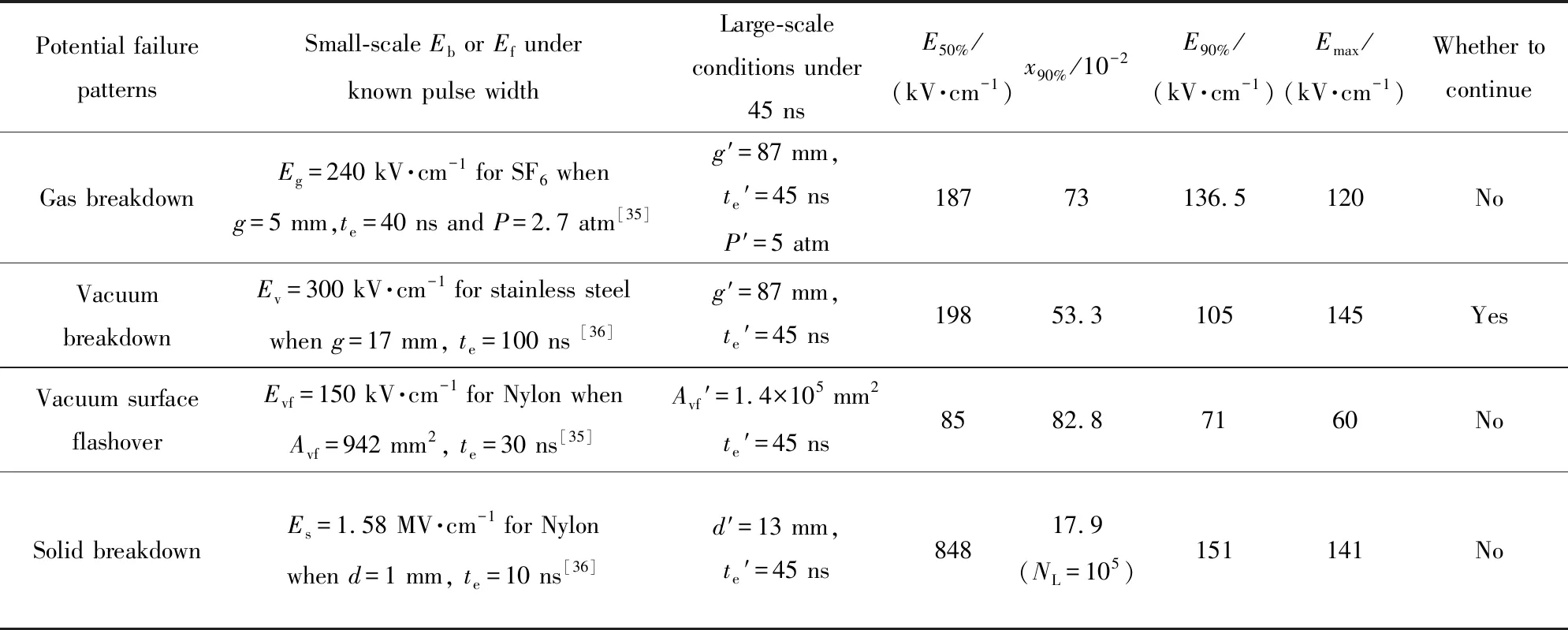
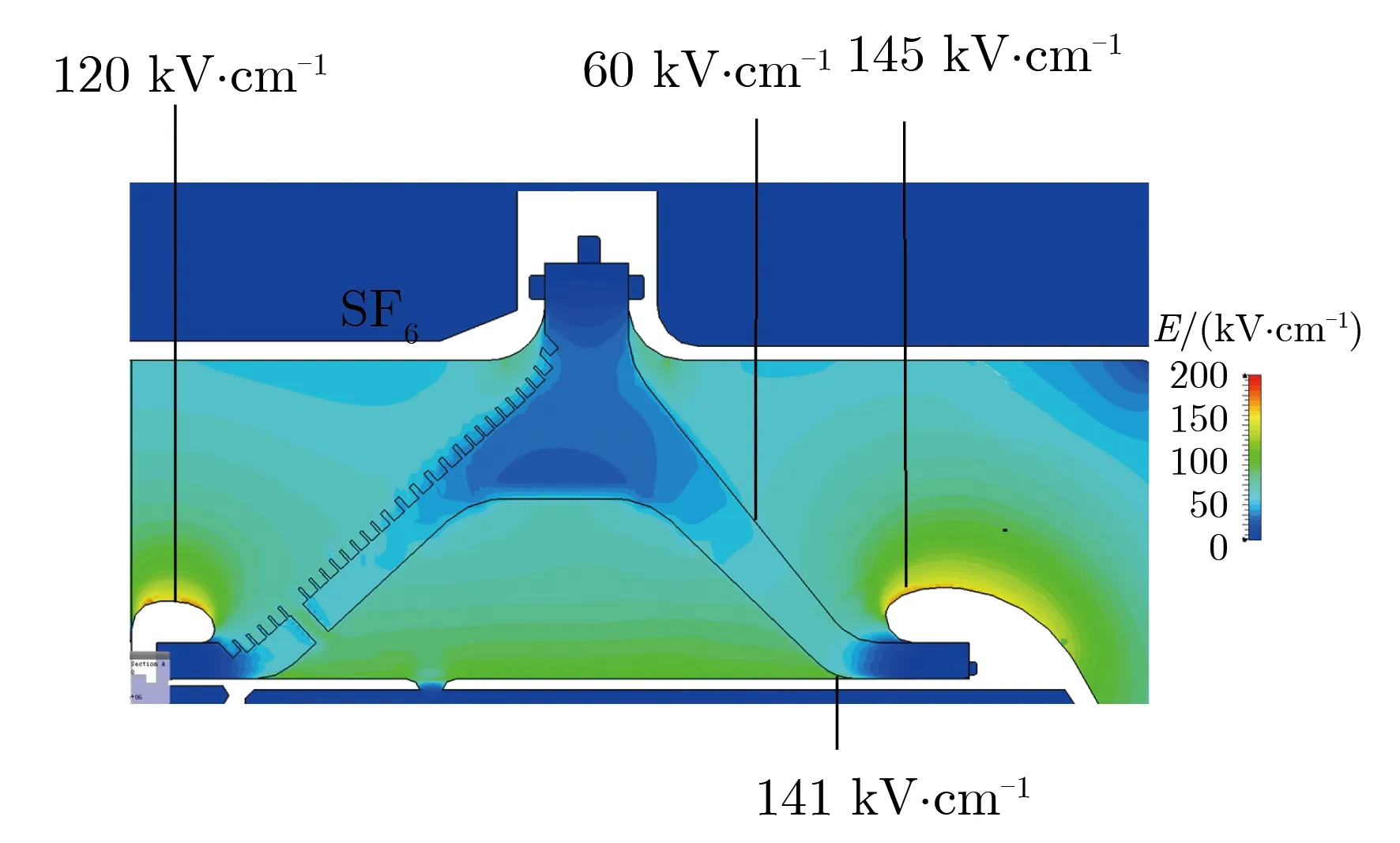
鉴于此，对于给定的绝缘结构，可定义可靠度不能低于一定值Rc，如Rc=36.8%。当R

min{Rsolid,Rfluid,Rinterface}|N

(1)

若将式(1)表达成以寿命和电场为变量的形式，需知道每种绝缘形式的可靠度随外施电场及寿命的变化关系。

2 绝缘设计的理论基础

脉冲功率装置中绝缘设计方法的理论基础有2点：一是描述短脉冲下固、液、气、真空击穿及沿面闪络阈值的统一计算公式；二是描述不同绝缘形式的可靠度计算公式。

2.1 统一阈值计算公式

限于实验条件，研究者通常只能获得小样品、已知脉宽下各类绝缘实验的击穿数据，尚无法直接获得大尺寸、应用脉宽条件下的实验数据。文献[29总结了短脉冲下固、液、气、真空击穿及真空沿面闪络阈值的统一计算公式，表示为

(2)

其中：te为电场有效耐受时间；Ω为绝缘结构的尺寸参数，如厚度、体积、电极面积级电极间隙等；E为击穿概率为50%时对应的电场强度，对于不同绝缘失效形式，求得大尺寸用脉宽条件的电场阈值E(Ω2,t2)，统一公式的尺度变换和时间变换示意图如图2所示。每种绝缘形式失效时电场阈值的计算公式如表1所列。需说明的是：(1)表2中所列出的公式均有适用范围，Ω含义不同，α、β取值不同，具体见表2，应用表2中的公式，可将小尺寸已知脉宽的实验数据E1(Ω1,t1)拓展，具体见文献 [29]；(2)式(2)中β的取值就是Weibull分布的形状参数m，证明见文献 [29]；(3)E(Ω1,t1)是一系列击穿数据的平均值，代表的是击穿概率为50%时的击穿阈值，变换后，E(Ω2,t2)所代表的击穿概率同样也是50%。

图2 统一公式的尺度变换和时间变换示意图Fig.2 Transition from (E1, t1, Ω1) to (E2, t2, Ω2)

表2 用于失效计算每种绝缘形式电场阈值的公式Tab.2 Formula to calculate electric field for insulaiton failure patterns

2.2 可靠度与外施电场之间的关系

文献[30]给出了2参数Weibull失效概率分布，表示为

(3)

其中，E0为特征电场强度，代表击穿概率为63.2%(或可靠度为36.8%)时电场强度。对于电介质击穿或闪络现象，仅受电场E影响的击穿概率即失效概率。再由于同一产品或零部件的失效状态与可靠状态互补，即F+R=1，可得到R(E)，表示为

(4)

进一步，文献 [31]还从3参数Weibull分布出发，得到脉冲数与电场同时为变量时的可靠度，表示为

(5)

其中：EBD为击穿概率为50%(或可靠度为50%)时击穿电场强度；NL为额定寿命。

式(4)适用于放电中无累积效应发生的绝缘失效情况。累积效应指结构劣化和放电通道长度等随脉冲数增加的现象。式(5)适用于放电中有累积效应发生的绝缘失效情况，典型的如固体电介质击穿等。对于气体击穿、液体击穿、真空沿面闪络及固-液沿面闪络等情况，虽在绝缘子及电极表面有劣化情况，但由于绝缘媒质的流动性和无定型性，这种累积效应较轻微，随脉冲数增加不显著，可近似地将这些绝缘失效方式按无累积效应的情况对待。从可靠度角度，无累积效应是认为可靠度不随寿命发生变化，即R仅受E影响。

实际中，通常以寿命和可靠度来规定零部件或系统的可靠性，但这2个指标并不能直接指导绝缘设计。工程中与绝缘设计直接相关的是外施电场。因此，需建立外施电场ER与可靠度R和寿命NL之间的定量关系。根据式(4)，可得到

(6)

由式(6)可得ER与R之间的关系，表示为

(7)

由式(5)可得ER与R及NL之间的关系，表示为

(8)

定义xR=ER/E为归一化外施电场。对于气体击穿、液体击穿、真空击穿及真空沿面闪络等累积效应微弱的绝缘失效形式，可采用式(7)计算xR，结果如表3所列；对于累积击穿效应显著的固体绝缘失效形式，利用式(8)，令m=8，计算xR，结果如表4所列。

表3 气体击穿、液体击穿、真空击穿及真空沿面闪络等绝缘形式对应的归一化外施电场Tab.3 Normalized electric field for vacuum, liquid, gas breakdown and vacuum surface flashover

表4 不同寿命固体绝缘(m=8)结构的归一化外施电场Tab.4 Formula to calculate electric field for insulation failure patterns

3 混合绝缘结构设计的一般步骤

3.1 一般步骤

结合之前的论述，本文总结提出了脉冲功率装置中混合绝缘的一般设计步骤：

(1)分析所设计绝缘结构中包括的潜在绝缘失效形式，如固体击穿、真空击穿及真空沿面闪络等；

(2)通过统一公式，计算出相同绝缘形式50%可靠度对应的击穿(或闪络)电场强度阈值；

(3)结合式(7)和式(8)，计算出给定可靠度下归一化外施电场强度，将该值与50%击穿电场(或闪络电场)强度相乘，便可计算出不同绝缘形式的最大外施电场；

(4)通过仿真，获得现有结构模型的2维电场分布，并提取出关键位置的最大电场强度；

(5)比较不同绝缘形式的给定外施电场和仿真电场，如仿真电场小于给定外施电场，则设计合格，否则需重新优化。

3.2 举例分析

以一个Tesla型脉冲功率源中的多功能传输线绝缘子[32]为例，对上述绝缘设计方法及步骤进行说明。

图3为某Tesla型驱动源的输出线单元示意图。输出线为同轴结构，功能是向返波管(backward wave oscillator，BWO)负载输出660 kV，45 ns的电脉冲。多功能传输线绝缘子安装于不锈钢传输线内部，主要作用有：(1)支撑并隔离同轴线内、外筒，为负载提供真空环境；(2)提供“绝缘”内、外筒之间的高电压；(3)通过绕制在开关侧绝缘子表面的接地电感隔离主脉冲之前的预脉冲。

图3 某Tesla型驱动源的输出线单元示意图Fig.3 Schematic diagram of a multi-functional HV vacuum insulator with BWO

图4为多功能传输线绝缘子3维模型。绝缘子截面呈“人”字型，材料为Nylon，左侧充5 atm(1 atm=1.013 ×105Pa)的SF6气体进行绝缘，右侧隔离气体，为返波管负载提供真空环境。绝缘子外径为400 mm，内径为180 mm，两侧45°设计。绝缘子两侧设计有压环，安装后用于固定绝缘子和屏蔽绝缘子与内筒三结合点处的电场，开关侧和真空侧压环与外筒之间的距离均为87 mm，绝缘子最薄位置的厚度为13 mm。要求绝缘子以不低于90%的可靠度工作105个脉冲。根据第3.1节中给出的设计步骤，进行绝缘设计：

(1)识别潜在绝缘风险。该绝缘子主要面临左侧开关压环与外筒之间的气体击穿、右侧阴极屏蔽环与外筒之间的真空击穿、绝缘子右侧表面的真空沿面闪络及绝缘子右侧最薄区域的体击穿4种绝缘失效风险。

图4 多功能传输线绝缘子3维模型Fig.4 3-D model of multi-functional vacuum insulator

(2)计算4种绝缘形式的E。以气体击穿为例，根据文献 [33]，在SF6条件下，当g=5 mm，te=40 ns，P=2.7 atm时，有Eg=240 kV·cm-1。利用表2所列的气体击穿阈值计算公式，可计算出当g′=87 mm，te′=45 ns，P′=5 atm时的击穿电场Eg′=187 kV·cm-1，其余绝缘形式的E如表5所列。

(3)计算4种绝缘形式在给定条件下的最大外施电场。同样以气体击穿为例，m=6。当R=90%时，根据表3，查得归一化外施电场x90%(m=6)=73.0%，所以SF6气体90%可靠度对应的电场强度E90%=E·x90%=187 kV·cm-1×0.73≈136.5 kV·cm-1，其余绝缘形式的最大外施电场计算结果如表5所列。

(4)通过电场仿真软件获得传输线绝缘子初始模型的2维电场分布，如图5所示，并提取出关键位置的最大电场。如，可能发生气体击穿的开关侧压环表面电场为120 kV·cm-1。

表5 多功能传输线绝缘子设计过程中的最大外施电场计算结果Tab.5 xR in design process of the multi-functional vacuum insulator

图5 多功能传输线绝缘子初始模型的2维电场分布Fig.5 2-D electric field distribution of the multi-functional vacuum insulator

(5)比较给定外施电场和仿真电场，决定是否继续进行优化。通过比较发现，除真空侧阴极屏蔽环表面的电场强度(145 kV·cm-1)超过90%可靠度对应的外施电场强度(105 kV·cm-1)外，其余关键位置的最大电场强度均小于90%可靠度所对应的外施电场强度，所以仍需优化，目标是减小阴极屏蔽环表面的电场，使其小于或等于给定的，由可靠度和寿命指标计算出的电场强度(105 kV·cm-1)。表5中列出了多功能传输线绝缘子设计过程中的关键参数。

4 结论

本文提出了脉冲功率装置中混合绝缘结构设计的一般方法，基本思想是将绝缘结构看成一个整体，通盘考虑各种绝缘形式的可靠度和寿命。该方法的基本步骤为：(1)识别混合绝缘结构的潜在失效风险；(2)计算出各绝缘形式50%可靠度所对应的击穿电场或沿面闪络电场；(3)计算出给定可靠度和寿命条件下的外施电场；(4)通过仿真获得混合绝缘结构关键位置的最大外施电场；(5)比较给定外施电场和仿真外施电场，决定是否进行下一步优化。该方法适合设计脉冲功率装置中常见的固-液、固-气、固体-真空等混合绝缘结构。