基于模糊聚类处理月亮型数据的研究与实现

侯冀超 谢成心 孟凡兴 温秀梅,2*

(1.河北建筑工程学院，河北 张家口 075000；2.张家口市大数据技术创新中心，河北 张家口 075000)

0 引 言

传统K-Means算法属于划分聚类，通过提前设定聚类数目不断迭代聚类中心直到满足迭代条件.随着模糊集理论的发展，RusPini提出了模糊划分的概念，针对不同领域的应用，在K-Means算法的基础上，提出了模糊聚类.模糊聚类应用于多个领域，如天气预报、农业、林业以及图像分割等.

模糊聚类与K-Means最大的不同在于K-Means聚类算法严格计算每个数据点的簇归属，非此即彼的关系体现了硬聚类的思想.但是现实数据中，并非如此，模糊聚类通过对聚类中心的不确定描述，更加客观地反应了数据的归属，在各个领域的应用中，模糊的概念更真实地反应客观世界，从而成为聚类分析的主流.因此模糊聚类引入了“隶属度”的概念，使得数据中的对象可以同属于多个簇，属于软聚类的思想.

FCM聚类算法通过不断迭代聚类中心、隶属度以及目标函数J，得到最优的聚类结果.王玲等人提出了一种基于密度的模糊自适应聚类算法(A density-based Fuzzy adaptive clustering algorithm,DFAC)，通过计算全局的自适应半径，根据有效性指标(|V(k)-V(k-1)|<ε)确定最优的聚类中心个数以及聚类中心点的位置.其次通过分别更新聚类中心和隶属度矩阵以及目标函数J，直到满足迭代条件(|J(t)-J(t-1)|<ε)得到更新t次后的最佳聚类结果.然而，通过不断迭代聚类中心以及隶属度的思想对处理月亮型数据集表现欠佳，故本文提出基于模糊类中心点的近邻点扩展聚类算法，结合了FCM以及密度聚类(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)的思想.

本文算法设计思想为：首先通过不断迭代聚类中心以及隶属度，直到隶属度不再发生较大的变化，从而得到最优聚类中心以及隶属度，其次利用DBSCAN的点扩展思想，利用最优的聚类中心点的近邻点进行邻域扩展，将扩展的样本点划分到同一簇内，最终得到聚类结果，实验研究结果可以成功将月亮型数据进行划分，解决了FCM算法以及DFAC算法对月亮型数据表现较差的问题.下面围绕相关概念以及本文所提思想、操作步骤、实验结果进行说明.

1 相关知识

1.1 基本概念

密度聚类以及模糊聚类的基本概念如下所述：

定义①：ε-邻域是指存在xi∈数据集R，其ε-邻域指数据集R中与xi距离小于ε的样本个数，即N-ε(xi)={xi∈R | dist(xi,xj)<=ε，(dist表示两点之间的距离)}.

定义②：隶属度是指对论域内，U中的任意对象x，存在数A(x)∈[0～1]与对象相等，则A是U上的模糊集，A(x)为x对A的隶属度.A(x)相当于函数，当A(x)→1，则隶属度越高，反之越低.

定义③：密度可达、相连是指对xi与xj，存在样本p1～pn，p1=xi、pn=xj且pi+1由pi密度直达，则xi由xj密度可达.若有xi和xj均与xk密度可达，则xi与xj密度相连.

1.2 FCM算法

FCM属于划分聚类，主要思想是将对象划分到同一簇内，同一簇内对象相似度高，反之，相似度小.通过“隶属度”判断对象的归属.模糊聚类FCM首先对是否超过最大迭代次数进行判断，若满足迭代条件，则返回聚类结果，若不满足，则继续计算聚类中心C(k)，以及更新隶属度矩阵u(k+1)，判断是否满足迭代条件，若满足，返回聚类结果，若不满足，则令迭代次数加一.

2 NNE-FC算法相关概念

2.1 NNE-FC算法思想设计

本文借鉴了FCM和DBSCAN聚类算法的思想，首先不断迭代聚类中心点Ck与隶属度矩阵Uk直到满足迭代条件，其次通过最优的聚类中心点搜寻与类中心点距离最近的对象，对搜寻到的对象进行邻域扩展，以聚类中心点到最近点的距离为邻域半径(Eps)，将邻域内不小于Minpts的数据点进行邻域扩展，将扩展后的数据划分到同一簇内，最终得到聚类结果，通过调整兰德系数(Adjusted Rand index)对模型进行性能评估，兰德系数的取值范围为[0,1]，值越大，聚类结果与真实结果越吻合.基于模糊类中心点最近点扩展聚类算法的主要步骤如下：

①初始化隶属度矩阵uij

(a)更新聚类中心点C(k)；

(b)更新隶属度矩阵uij(k+1)；

(c)重复(a)、(b)步骤直到满足迭代终止条件，得到最终聚类中心点C；

②对聚类中心点C进行逐步扩展

(d)计算聚类中心点与最近点之间的距离εi；

(e)以距离εi为半径作圆，将ε-邻域内不小于Minpts的对象进行扩展，将扩展的对象划分到同一簇内；

(f)重复(d)、(e)步骤直到聚类中心点C处理完毕.

2.2 初始化隶属度矩阵以及更新隶属度u

输入超参数提前设定聚类中心的数目确定初始化隶属度矩阵，以每个数据点对聚类中心点的隶属度进行随机分配，其中，每个数据点对应的各个聚类中心点之和为1.公式为：

(1)

式中，m为数据点的个数，n为聚类中心的个数.

通过引入拉格朗日约束条件得到更新的隶属度uij公式：

(2)

式中，uij为xi与cj更新的隶属度，m为超参数，是提前设定的聚类中心个数.当(xi-cj)越小时，即点xi距离聚类中心点cj越近时，分母变小，整体隶属度uij越大.

2.3 聚类中心点c

通过引入拉格朗日约束条件得到更新的聚类中心点cj公式：

(3)

式中，n为数据集中对象的个数，uij为xi与cj之间的隶属度，cj为第j个聚类中心点.m为超参数.

2.4 迭代终止条件

在不满足超参数所设置的最大迭代次数Iter_num(默认为100)时，迭代的终止条件为：

maxij{|uij(k+1)-uij(k)|}≤δ

(4)

式中，δ为超参数，uij(k)为第k次迭代的隶属度.

2.5寻找cj的自适应半径

通过达到迭代终止条件获取到最优的聚类中心点cj后，计算与聚类中心点cj距离最近的数据点xi，则自适应半径公式为：

(5)

式中，n为数据中对象个数，cj为第j个聚类中心点，xi为数据中的对象，delta为超参数.

2.6 邻域查询

以自适应半径作圆，将邻域内不小于Minpts个数的对象放入邻域内，逐步对邻域内的对象进行扩展，将扩展得到的对象划分到同一簇内，直到邻域内的对象查询完毕.

2.7 基于模糊类中心点最近点扩展聚类算法伪代码

基于模糊类中心点最近点扩展聚类算法伪代码如下所示.其中，D表示数据集，clust_num表示要聚类中心点的数目，iter_num表示最大迭代次数，delta表示扩充聚类中心点邻域半径，Minpts表示核心点的阈值，即形成簇所需的最小核心点数目，m为计算uij与cj的超参数，C_last表示最优的聚类中心点，cluster表示对象所在的簇.

Input：D，clust_num，iter_num，delta，Minpts，m

Output：C_last，cluster

Func NNE-FC(D,clust_num,iter_num,delta,Minpts,m)

{

//计算最优聚类中心点C_last

Initial_U

while there have iter_num to circulated{

cj= Cen_Iter from uijm,xi

uij= U_Iter from xi,cj,ck,m

until maxij{|uijk+1-uijk|}<=δ

} return C_last

while len(C_last){

//计算自适应半径eps与邻近点C_last_nearobj

C_last_nearobj = utilizing sklearn.KDTree

eps = (C_last_eps utilizing (sklearn.KDTree,C_last_nearobj) from D , C_last) + delta

expand C_last_nearobj if (points <= eps)

}return cluster

}

end

3 实验环境与结果

3.1 实验环境

本文提出的NNE-FC是通过Python语言在Anaconda环境中实现的，由matplotlib库绘图与Excel实现实验结果.实验环境：CPU为Intel(R)Core(TM)I5-7200U@2.5GHZ 2.71 GHZ，RAM为8.00GB(7.88GB可用).实验结果分别对FCM、DFAC算法以及本文算法进行了实验对比，对比数据在相同、公平且参数相同的环境下进行实验.

3.2 实验结果分析

实验为验证本文算法NNE-FC对数据集的通用性以及对月亮型数据集的聚类效果.实验一验证本文算法对数据集通用性；实验二验证算法NNE-FC对数据较少的月亮型数据集的聚类效果；实验三验证算法NNE-FC对数据中含有高斯噪声标准差的月亮型数据集的聚类效果.其中，实验中“黑色圆点(·)”代表原始散点图，“彩色圆点”代表同一簇内的数据点，“★”代表聚类中心点.

实验一采用sklearn.make_blobs数据集，共50个数据点，真实标签应分为三类.由于DFAC算法因自适应确定簇的数目，故将簇分为两类，图1(c)DFAC的兰德系数为0.5689，聚类结果较差.FCM聚类算法与本文NNE-FC算法因输入超参数确定簇的数目，成功将数据集识别为三类，图1中(b)FCM与(d)NNE-FC的兰德系数均为0.9399，聚类效果良好，但仍会将部分对象进行错误划分，见图1.

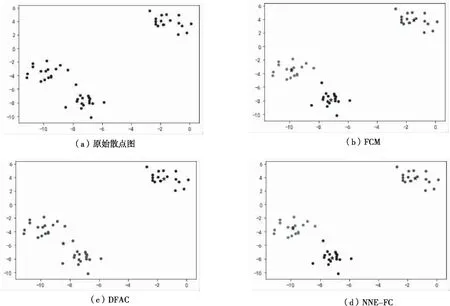
图1 实验一聚类结果

实验二采用sklearn.make_moons数据较少的数据集，共20个数据点，数据中高斯噪声的标准差“noise”为0，真实标签应分为两类.FCM算法与DFAC算法对月亮型数据集聚类结果较差，图2中(b)FCM与(c)DFAC的兰德系数均为0.1133，而本文NNE-FC聚类算法成功将月亮型数据集进行划分，图2中(d)NNE-FC的兰德系数为1.0，聚类效果良好，见图2.

图2 实验二聚类结果

实验三采用sklearn.make_moons数据集，共400个数据点，数据中高斯噪声的标准差“noise”为0.05，真实标签应分为两类.本文算法与FCM算法进行对比，结果显示本文NNE-FC聚类算法能够对月亮型数据进行识别，图3中(b)FCM算法的兰德系数为0.2431，而(c)NNE-FC的兰德系数为1.0，聚类结果良好，见图3.

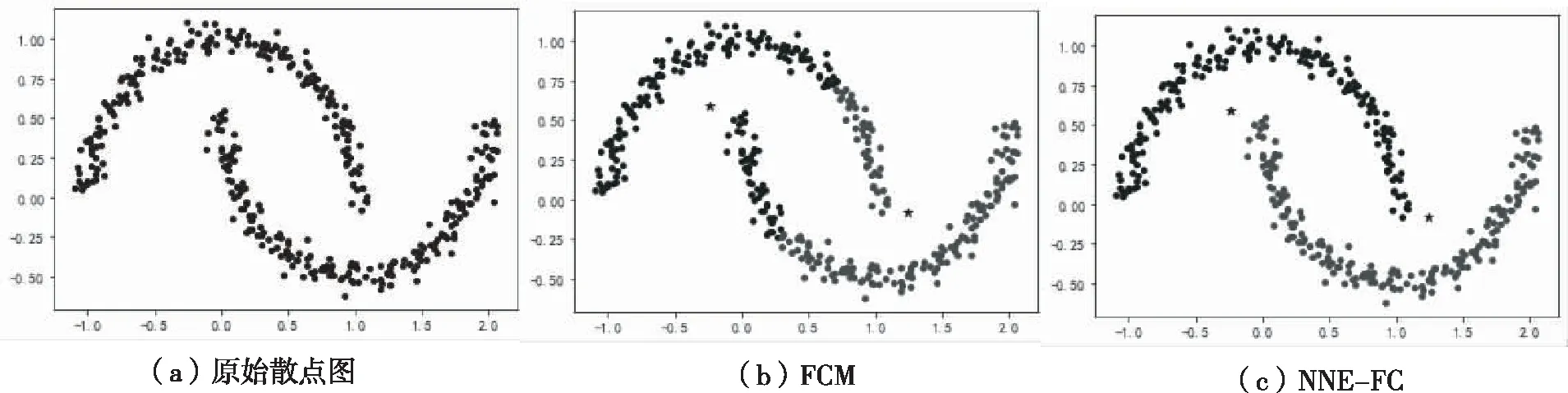
图3 实验三聚类结果

4 结束语

本文所提出的NNE-FC结合了FCM算法与DBSCAN算法的思想，继承了FCM与DBSCAN算法的优势，不仅可以识别多密度数据集，且对月亮型数据集的处理也有较好的聚类结果，改进了传统的FCM聚类算法无法识别月亮型数据集的问题.本文算法需要输入的超参数较多，对超参数的最佳选择仍有待提高，下一步将重点研究如何通过自适应或决策图的方式确定超参数的选择，进一步优化超参数的选择.