对称平面天线振子阵列技术研究

张长青

（中国移动通信集团湖南有限公司岳阳分公司，湖南 岳阳 414000）

0 引言

大规模相控阵天线是由几十或几百，甚至上千天线阵元组成的天线阵列，每个天线阵元上设置一个移相器和一个功率放大器，从而使得波束宽度极小的赋形波束的传输距离，可以从几米、几十米，延长到几千米，甚至几万米或更远，使之能用于移动通信及更远距离的卫星移动通信等，成为6G的关键技术之一。

对称平面天线将微带贴片平面用在对称天线上，将微带贴片平面易于集成和辐射波束宽度相对较小的优点，与对称线天线优秀的方向性相结合，若是作为大规模天线阵列的基本振子，由此形成的集成天线阵列，技术上不仅方便大规模辐射振子的集成，产生的波束赋形效果也会更加优秀，特别适应毫米波段范围以内的应用。

传统的集成天线阵列技术采用的是微带贴片天线振子，虽然微带贴片振子可以做得较小，也便于集成，但微带贴片振子天线是闭合式天线，贴片的两面一片在前，一片在后，电磁波只能从微带贴片振子的前后贴片之间的四周侧面向外泄漏，这种泄漏辐射生产的波束赋形效果有限，由此形成的集成天线阵列所产生的波束赋形效果并不理想。另外，微带贴片天线的结构实际上是一种电容模式，因而是一种容抗式天线，天线振子的容抗使其可以产生较为严重的容抗式虚功输出，甚至还会产生较为严重的寄身振荡，极大地影响了天线的辐射效果。

传统的对称线天线是一种开放式的阻抗式天线，辐射功率全部为实功，没有任何虚功。而且还是一种典型的偶极子天线，天线辐射产生的方向图，是所有线天线中最理想的模式之一。但因天线振子长为半波长的倍数，当辐射波长较大时，天线架构也比较大，一定程度上限制了它成为集成天线阵列的设计。但当辐射波长是毫米波段时，这种情况就得到了根本解决。因此，将对称贴片天线与集成天线阵列结合起来后，可以发挥微带贴片天线、对称天线和集成天线阵列的共有优点。

1 对称线天线的方向图公式

根据电磁场理论[1]，当最大幅值为Im的信号电流I，在z≥0范围内的值为I(z)=Imsin[k(l-z)]，在z<0范围内的值为I(z)=Imsin[k(l+z)]，即在整个线天线中的信号电流是：Imsin[k(l-|z|)]时，线天线对称臂上沿z轴分布的辐射电流可以用驻波表述。若线天线上的辐射信号是角频率的ω谐波，则对称线天线振子上从中间向辐射臂两端流动的馈电激励源信号电流可以简单地表示为：I(z,t)=Imsin[k(l-|z|)]sin(ωt)。

根据图1所示，当线天线中位于Q点处的电流元Idz，距离观察点P(r,θ,φ)的距离r远大于线天线长2lz时。线天线信号中电流元Idz在观察点P处的电场元可以表示为[2]：

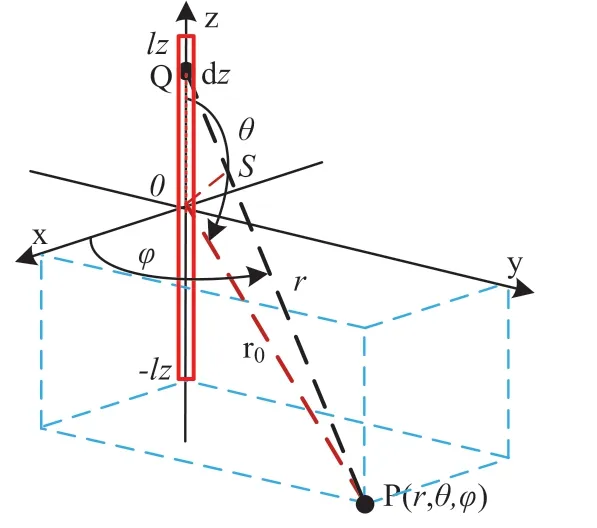
图1 对称线天线电流元的辐射示意图

式中η为比例常数，k=2π/λ是波数，λ为信号波长，θ是线天线俯仰角，exp(-jkr)是电流元Idz辐射的电磁波从Q点到P点的波程差引起的相位差。

由于r>>lz，根据泰勒展开，若取1/r最低项，可取分母中r为天线中点0到观察点P的距离r0；但因指数中的r与相位相关，可取r=PS+SQ=r0+zcosθ。则式(1)为：

再对上式积分。显然，虚部是奇函数，积分为零，实部是偶函数，可以对称处理，则上式积分简化为：

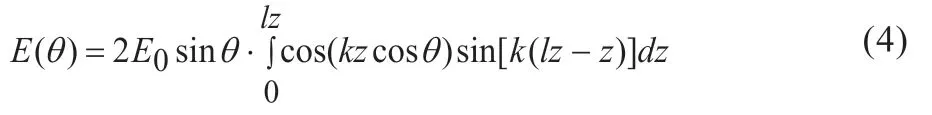
再根据三角函数恒等式sinθcosφ=[sin(θ+φ)+sin(θ-φ)]/2和三角函数积分公式∫sinxdx=-cosx+c展开整体得：

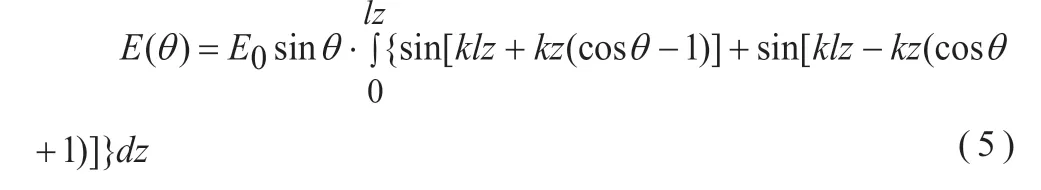
再根据三角函数积分公式∫sinxdx=-cosx+c整体得：

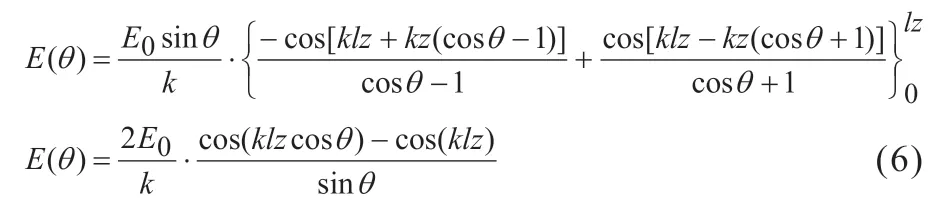
最后得对称线天线在P处的辐射电场：

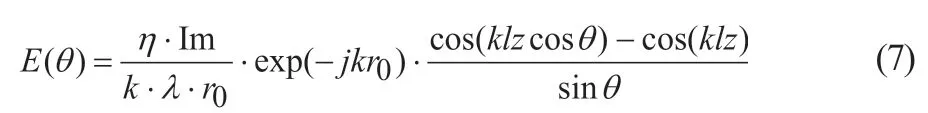
式(2)中对应的线天线的方向图函数为：

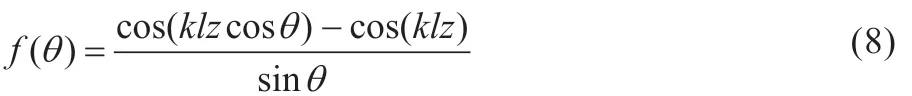
因为线天线长为2lz，当lz=λ/4时，线天线叫半波天线，其中klz=(2π/λ)(λ/4)=π/2，得半波天线方向图函数：

2 对称平面天线的方向图公式

（1）用线天线电流元方式求解

如图2所示，设对称平面天线平面的宽为2lx、高为2lz，平面中间绝缘，将平面分成上下两个平面振子，馈电激励电流产生的信号，从中间向上下平面的两端流动，然后再从两个平面振子辐射到空间。

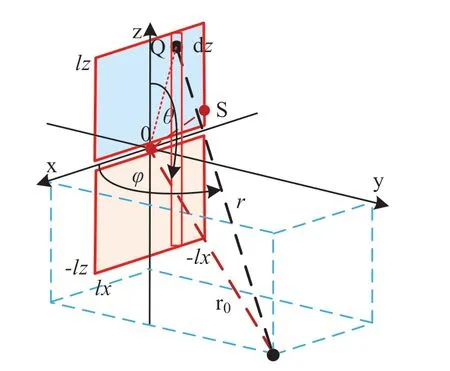
图2 对称平面天线电流元辐射示意图

若将图2所示的对称平面天线横向分成无穷个对称线天线，其中每个线天线上的辐射信号电流仍定义为I(z,t)=Imsin[k(l-|z|)]sin(ωt)，根据公式(1)，在Q处第i个对称线天线上的馈电激励信号电流元I(z)dzdx，则在远处P(r,θ,φ)产生的电磁场，可以表示为：

显然，式(11)无法用初等函数完成二重积分的。

（2）用线天线元方式求解

若仍然将图2所示的对称平面天线横向分成无穷个对称线天线，但其中的每个线天线仅当作一个线天线元，这样求解问题就可以简化了。

2.1 定义沿x轴上的信号电流不变

设式(2)为对称面天线的线天线元dEθ，即：

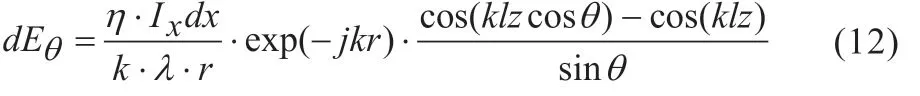
其中Ix=Im定义为常量，分母中的r同样用r0取代，指数中的r用r=r0+xcosφ取代，则式(12)可表示为：

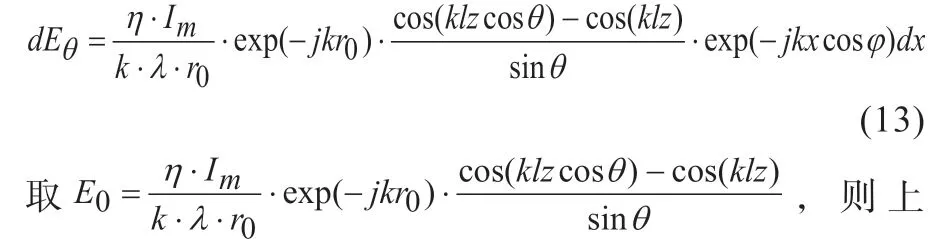
式为：

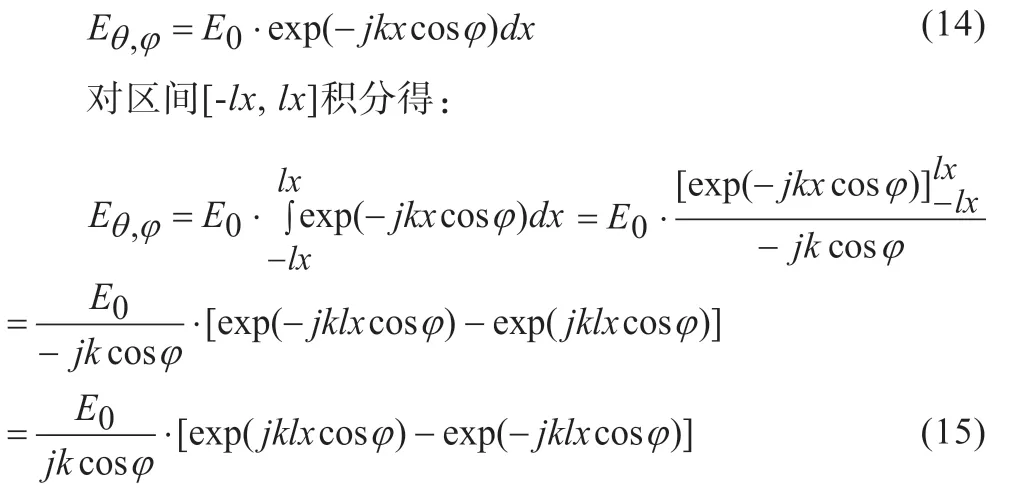
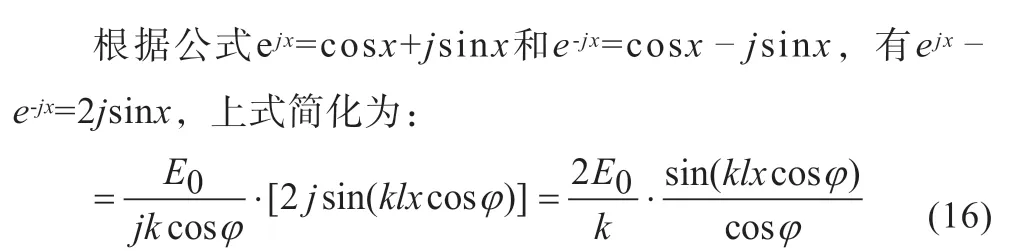
最后得在对称面天线在P(r,θ,φ)处的辐射电场为：

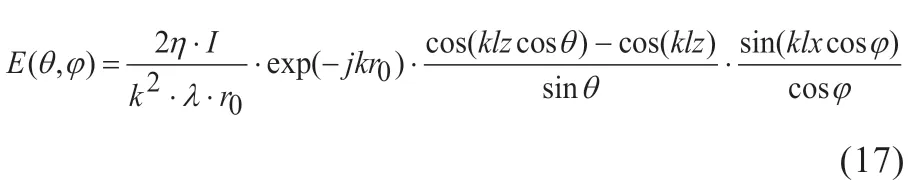
其中的方向图函数如下：

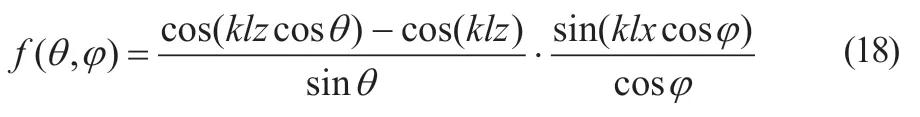
图3所示分别为线形对称天线（振子）式(3)和平面对称天线（振子）式(18)计算得到的归一化三维方向图和二维极坐标归一化方向图。在方向图函数的解析中，对称线天线振子和对称平面天线振子的高都为λ/2，对称平面天线振子的宽为λ2/5。

从图3可以看出，对称平面天线与对称线形天线的高一样，都是半波长，但对称平面天线的宽为是五分之二波长，因而只影响了水平方向图，使对称线形天线的圆形水平方向图，变成了对称平面天线的椭圆水平方向图，而且非常明显，即对称平面天线水平方向图的短半轴，与长半轴相比，至少小了10%以上。所以，虽然对称平面天线和对称线天线的水平方向图都是全向的，但前者明显优于后者。

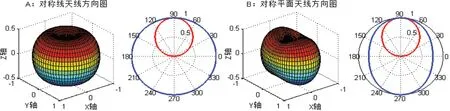
图3 对称线天线和对称平面天线方向图比较

2.2 用FDTD检验式(18)的正确性

FDTD（Finite Difference Time Domain，时域有限差分）是一种基于时间和空间、对Maxwell旋度方程进行有限差分离散、具有两阶精度、用中心有限差分格式近似代替微分形式的迭代数值计算法。FDTD将Maxwell微分方程在时空两域同时差分，在空域对电场和磁场用蛙跳方式交替计算，在时域通过更新方式模拟场强变化。FDTD分析电磁场因需考虑研究对象的几何参数、材料参数，计算精度、复杂度和稳定性，模拟精度较高。FDTD模拟空间电磁性质的参数按空间网格给出，只需给定相应空间点的媒质参数，就可以模拟复杂的电磁结构。FDTD在适当的边界和初始条件下解有限差分方程，用清晰的图像描述复杂的物理过程，可直接反映电磁波的时域特性，可表现非常丰富的电磁场的时域信息，是现代电磁场研究的重要方法。

FDTD网格剖分采用Yee提出的在空间和时间都差半个步长的结构方式，通过蛙跳步骤用前一时刻的磁、电场值得到当前时刻的电、磁场值，并在每一时刻将过程算遍整个空间，从而得到整个空间中随时间变化的电、磁场的时域解。若对时域解用Fourier变换，可得到相应的频域解。虽然电磁场的作用区域无限，但FDTD的计算空间有限，即由Yee元胞组成的Yee网格数量有限，必须在FDTD总场区的边界设置电磁场吸收区域，如近似吸收边界MUR和完全匹配吸收边界PML，其中PML吸收边界的完全匹配性，使得传播到总场边界处的电磁场几乎全部吸收殆尽，仿真无限空间中的电磁波传播效果非常真实。采用FDTD和PML边界来分析适应5G需求的同时频收发天线间的电磁场传播，完全可以获得理想的效果。

图4所示用FDTD仿真得到的辐射波形，与图3所示的对称平面天线振子的建模条件一件，也是高为λ/2，宽为λ2/5。可以看出，图4D对应的水平和垂直方向图，与图3中平面对称振子方向图几乎一样，只是波形稍微窄了一些。由于FDTD建模与实际情况一样，因此理论上FDTD仿真更接近实际情况，由此可以证明，平面对称天线的解析式(18)是正确的，可以作为后期研究阵的参考。

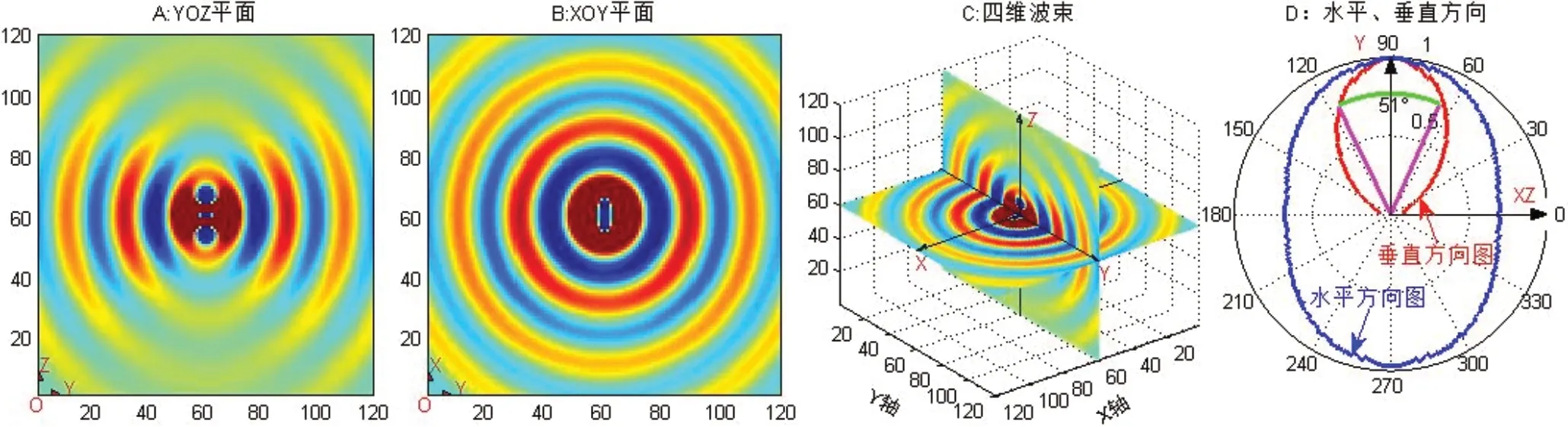
图4 FDTD仿真对称平面天线辐射的波形图

2.3 定义沿x轴上的信号电流与z轴一样

由于定义沿x轴上的信号电流与z轴一样，所以上下两个平面振子，需要分成左右两个小平面振子，如图5所示，从而在平面天线上的辐射信号电流，不仅在z方向是一个驻波，在x方向也是一个驻波，但求解方式仍然采用线天线元方法。

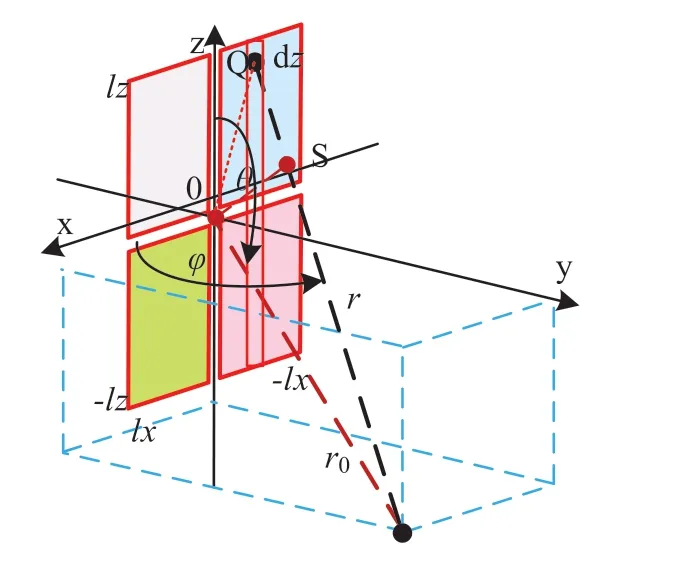
图5 对称平面天线辐射示意图

根据式(1)，在Q处第i个对称线天线上的馈电激励信号电流元I(z)dzdx，在远处P(r,θ,φ)产生的电磁场，可以表示为：

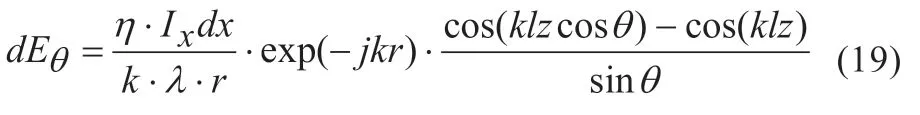
其中I定义与线天线一样，即I(x,t)=Imsin[k(lx-|x|)]sin(ωt)，分母中的r同样用r0取代，指数中的r用r=r0+xcosφ取代，则式(19)可表示为：

若对上式在区间[-lx,lx]中积分，虚部是奇函数，积分为零，实部是偶函数，可以对称处理，上式简化为：

又根据三角函数恒等式sinθcosφ=[sin(θ+φ)+sin(θ-φ)]/2和三角函数积分公式∫sinxdx=-cosx+c展开整体得：

式(18)和式(25)都会使水平方位方向图的由原来的圆形，变成椭圆形，而且椭圆的长轴位y轴，短轴位于x轴，但式(18)的短轴更短。也就是说，如果使平面振子上的辐射信号电流，仅按z方向呈驻波分布，在x方向尽量相同，则对称平面天线的方向图的水平方向性更好，见图6所示，而且振子上的辐射信号电流也更易实现。所以，在设计对称平面天线面时，应该采用式(18)对应的沿x轴上的信号电流不变，沿z轴上的信号电流为驻波分布方式，这也好理解，因为沿x轴的信号电流为驻波，则x轴向边缘处的信号电流为零，从而影响辐射效果。

图6 当z轴上信号电流为驻波时，x轴上信号电流不变和为驻波时的方向图

3 对称平面天线面阵的方向图公式

3.1 对称平面天线振子线阵辐射电场

对称平面天线振子线阵可以分为平行振子线阵和共轴振子线阵[2]，如图7所示：

图7 4对称平面平行振子和3对称平面共轴振子线阵示意图

根据阵列乘积定理，在由N个线天线组成的平行振子线阵中，第n个线天线振子在观察点P处的电场为：

若取In=I0，则上为可简化为：

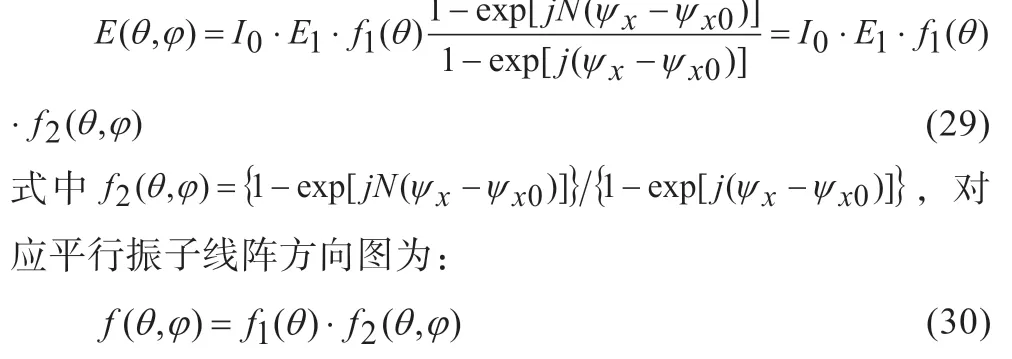
与此类推，设有M个线天线组成的共轴振子线阵，共轴振子线阵在观察点P处的电场：

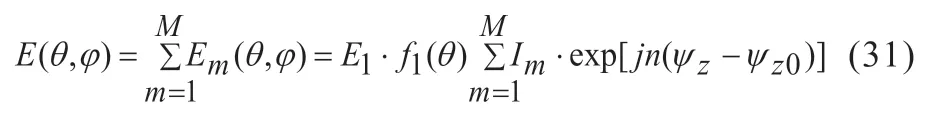
若取Im=I0，则上为可简化为：

3.2 对称平面天线振子面阵辐射电场

同理，根据阵列乘积定理，由N平行平面振子和M共轴平面振子组成的面阵（图8）在观察点P处的电场为：

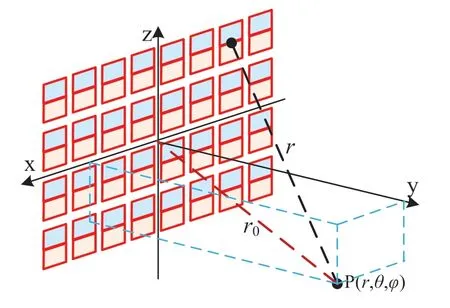
图8 8´4对称平面振子面阵示意图

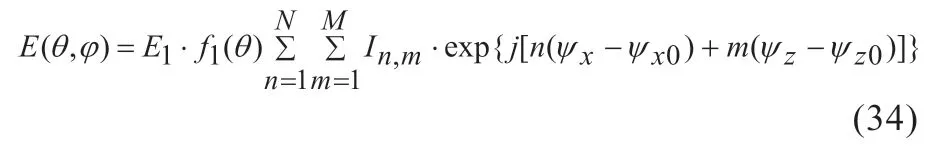
式中f1(θ,φ)为公式(18)，In,m是面阵中第（n、m）个振子激励电流的强度；ψx=k·dxsinθcosφ是相邻平行振子间的相位差，dx是振子水平方向间的间距；ψx0=-ax=kdxsinθ0cosφ0是观察点相对面阵的方位角；ψz=k·dzcosθ是相邻共轴振子间的相位差，dz是振子垂直方向间的间距；ψz0=-az=kdzcosθ0是观察点相对面阵的俯仰角。

若取In,m=I0，则上式可简化为：

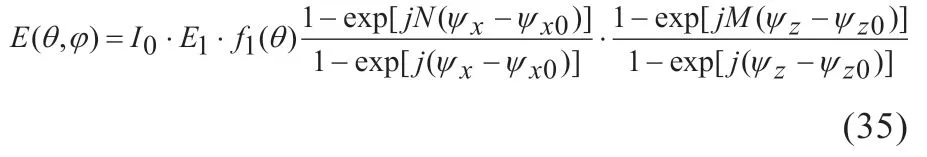
其中对应的面阵方向图公式为：

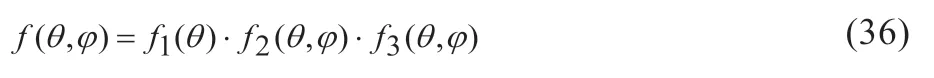
显然，从式(34)可知，调整ax和az或ψx0和ψz0，就等于调整了观察点的观察俯仰角和方位角，就可以确定面阵波束最大值辐射角的位置。若能使每个振子激励电流相位差ax和az连续变化，使其覆盖全部空域，就可以完成面阵波束最大值扫描全空间，这就是相近阵雷达的扫描原理。

4 对称平面天线面阵分析

对称线天线属于开放式天线，是一种全阻抗式辐射天线，其中半波长对称线天线又叫半波天线，天线振子辐射的方向图是偶极型，虽然水平方向图是全向形，但垂直方向图的方向性较强，标准方向角为74°，是一种广泛应用的线天线。由对称线天线阵元组成的二维面阵阵列的辐射方向图，是一种基于偶极辐射的方向性极强的定向辐射方向图，用较少的阵元可以获得品质较高的赋形波束。

对称平面天线属于贴片天线，也属于开放式天线，与传统的对称线天线一样，同样是全阻抗式辐射天线，振子辐射的方向图同为偶极形。但因平面振子的辐射特征，使得全向水平方向图的两边压缩，在对称线天线的基地上进一步增强了水平传输的方向性和辐射强度。另外，由于属于贴片天线，在小波长辐射领域，用对称平面天线振子组成阵列，还具有天线架构方面的集成性和小型化等优点。

为了分析对称平面天线面阵，鉴于计算机仿真时的性能限制，也为了方便直观赋形波束，设计了一款最简单的阵列，它由四个对称平面振子阵元组成，为了方便比较，还设计了一款由四个对称线天线阵元组成的阵列，通过对两者的计算和仿真分析，可以了解对称平面天线面阵的优点，见图9所示：

图9 2´2平面阵列

设线天线阵元的长2l z=λ/2，相邻阵元间的间距d x=d z=λ/2；平面振子阵元的长2l z=λ/2，阵元的宽2lx=λ2/5，相邻阵元间的间距dx-dz=λ/2。显然，两个阵列的设计完全同样，其中线天线阵元没有宽度设计。

如果选择5G典型频度28 GHz，对应的标准波长为108 mm，显然，这是基于毫米波应用的阵列，就是加上阵列底板边缘的宽度，这两款最简2´2平面阵列的大小结构均为120 mm´120 mm，面积大约只有拇指甲大。

根据式(36)，可以得到求得解析式对称平面天线阵列的方向图。若设lx=0，则式(36)可以简化为对称线天线阵列的解析式方向图函数。

图10所示便是根据式(36)分别得到的2´2线天线阵元阵列（见图10-A）和2´2平面天线阵元阵列（见图10-B）的方向图。可以看出，线天线阵元和平面天线阵元组成的阵列，两者的垂直方向角完全一样，但水平方向图的方向角前者是48°，后者是44°，前者比者降低了约10%。

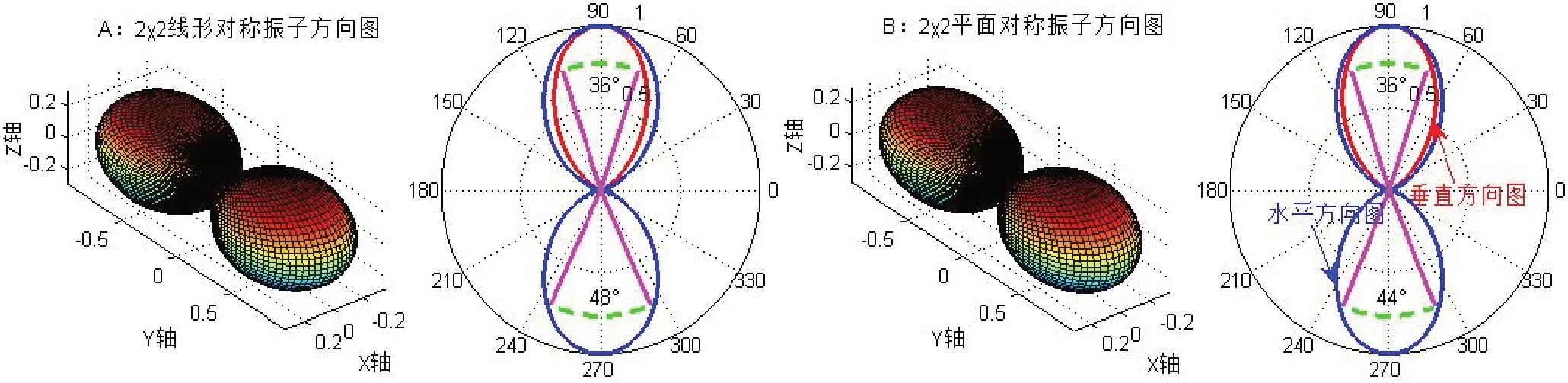
图10 用解析式计算的2´2对称线形振子和对称平面振子面阵方向图

如图11所示是用FDTD仿真的2´2对称平面振子面阵后来到的波形图和方向图，仿真中的建模与图中一样。

可以看出，图11-D中的垂直方向角与图9-B中一样都是36°，虽然水平方向角是46°，但这应该是仿真计算中的误差所至。由此可以证明，解析式(36)，在分析对称平面振子面阵时，准确性很高，具有很高的参考意义。

图11 用FDTD仿真的2´2对称平面振子面阵方向图

如图12所示，是利用式(36)计算的3´3和4´4对称平面振子面阵方向图。在面阵中，开放式平面贴片振子增加一点，方向图主辩的角度就会减少一些，仅仅分析面阵的水平方向图的夹角。当阵元是2´2时，水平角为44°；当阵元是3´3时，水平角为28°；当阵元是4´4时，水平角为20°。

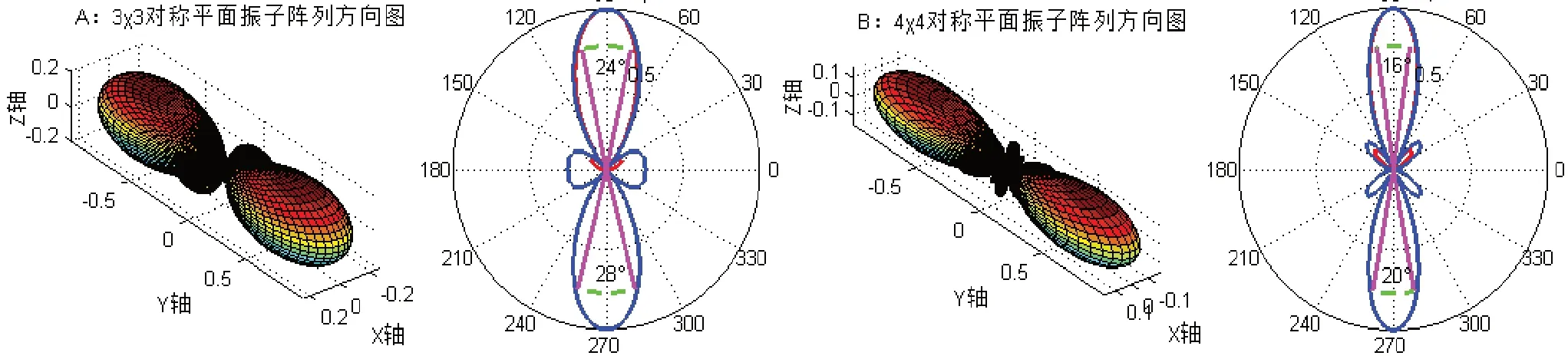
图12 用解析式计算的3´3和4´4对称平面振子面阵方向图

5 结论

在面阵方向图函数式(36)中，对称平面天线振子面阵和对称线天线振子平面的唯一区别，是平面天线振子方向图函数式(8)中的f1(θ,φ)，和线天线振子的方向图函数式(8)中的f1(θ)不同，式(18)中的f1(θ,φ)比式(8)中的f1(θ)多了一项与水平方位角φ有关的因子函数：

显然，式(37)是对称平面天线振子面阵方向图函数的重点，也是研究基于开放式对称平面振子面阵中的关键研究点，因为它直接决定了水平方向图。

图13-A所示图中，给出了三个贴片宽度，既lx=λ/6、λ/5和λ/4时，式(37)画出的方向图。图13-B所示曲线，表述的是lx在λ/30～λ/4之间连续变化时，图13-A所示椭圆短轴连续改变的关系。图13-B所示表述的是，对称平面天线振子贴片的宽度越大，方向图椭圆的短轴就越小，原则上讲方向图方向性越佳，对应的对称平面天线振子阵列的赋形波，也将越好。

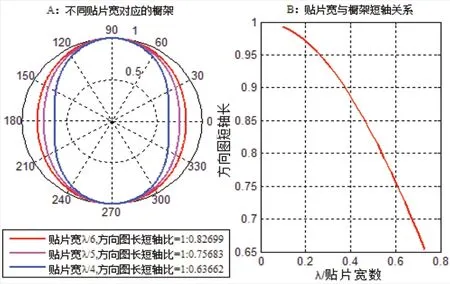
图13 式(37)表述的基本关系

因此，在设计对称平面天线振子阵列时，可以先参考图12，然后通过式(37)，得到平面天线振子贴片宽度的具体参数。

对称平面天线振子阵列的优点是，贴片振子方便集成化设计，开放式贴片没有虚功损耗，辐射中的水平方向角更小，并可以根据对称贴片宽的大小来调节水平方向角。这种集成化设计的阵列，非常适合毫米波辐射领域，在5G终端小型化设计中具有良好的选择优势。

最后补充一点，解析式中方向图基本上是对称分布，尤其是垂直方向图还是一个圆（如图3-B），而不是像FDTD仿真中是一个椭圆（如图4-D）。原因在于解析式简化时，将式(7)中分母中的r直接用r0代替了。而FDTD是直接对天线建模，所以仿真的方向图能够真实地反映出来。