基于K-means融合决策树分类算法的学生表现评价模型构建

许亚杰，梁靖涵

(郑州科技学院 信息工程学院，河南 郑州 450000)

0 引言

青少年是祖国的未来，是党和国家事业的接班人，正处于学习基础知识、认识世界的关键时期。研究表明，青少年时期的表现对青少年以后的人生有着深远的影响，因此，教育者应当重视学生表现[1]。目前，国内外专家学者对学生表现评价的研究已取得了一定的研究进展，相关的理论和实践性研究成果为本课题形成提供了重要的思想借鉴，但是，专门针对初级中学生家庭、行为和教学特征的研究成果尚不多见[2]。然而，初级中学生正处于是青春发育的关键期，存在着各式各样的问题，因此，教育者更要关注学生的成长，发现学生成长中的隐患，及时调整学生状态，促进学生全面发展。

1 K -means数据预处理

1.1 数据集

数据集来源于标准测试数据集，由加州大学欧文分校提供，数据集名称为Student Performance。该数据集通过使用学校报告和调查表进行收集，数据属性包括学生成绩、社会和与学校相关特征，数据集共有395条、33个属性。

1.2 数据探索与数据解释

本文重点研究影响学生学习表现的自身、家庭和学校因素。为保证数据集特征与分析内容相关性，需要对数据进行初步筛选。经过统计分析，总结出影响学生的如下因素：(1)在自身因素上，主要考虑健康状况、是否想要接受高等教育的意愿、是否恋爱；(2)在家庭因素上，家庭大小、父母同居状态、家庭关系质量；(3)在学校因素上，缺勤次数、每周学习时间、课外活动、上网时间、空闲时间等。

为此，本文提取了其中的主要因素对数据进行汇总，选择了famsize，Pstatus，studytime，activities，higher，Internet，romantic，famrel，freetime，goout，health和absences等12个属性作为特征评价指标。各属性及描述如表1所示。

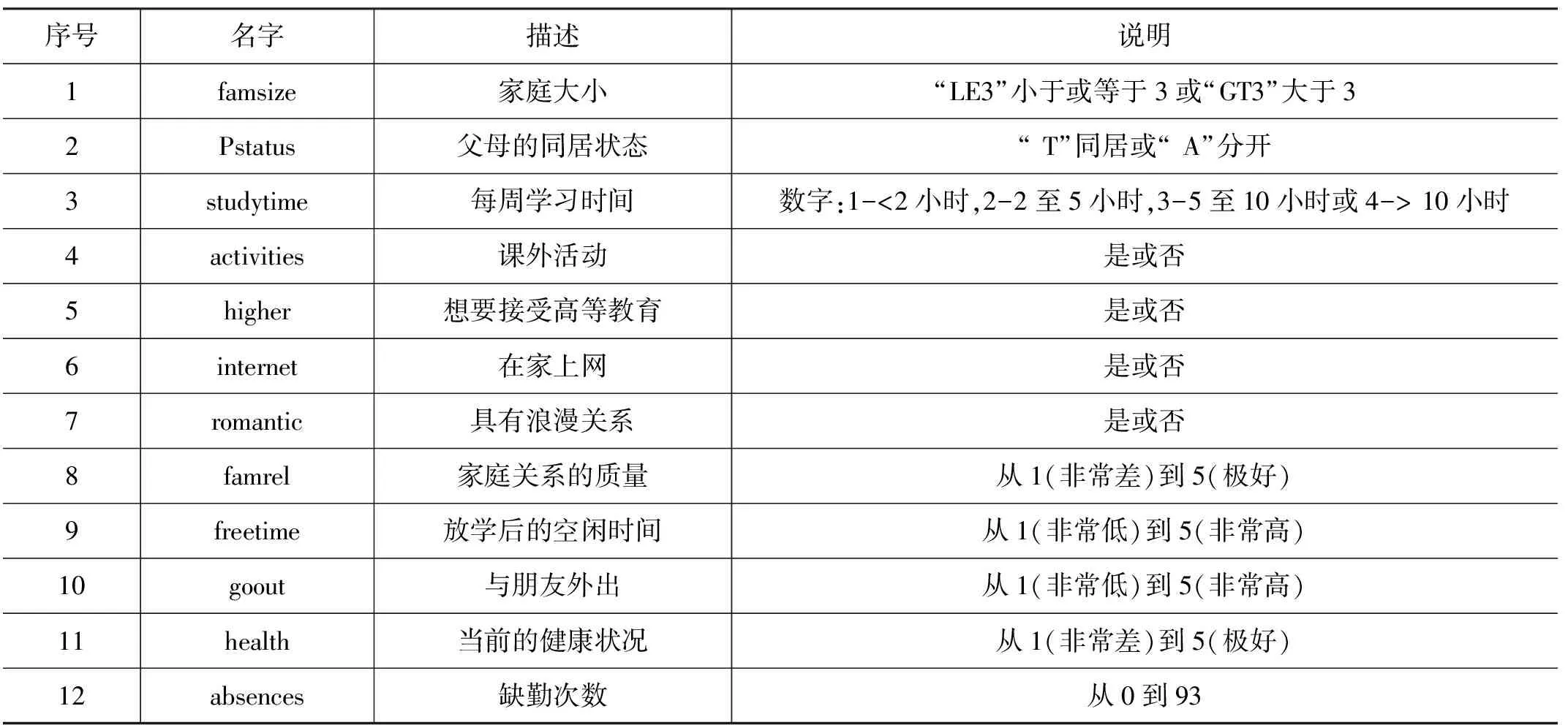
表1 数据集的属性与描述

1.3 数据清洗

数据清洗主要包括格式标准化、异常数据和重复数据清除和错误数据纠正。通过简单查询，可以看到本文所使用的学生表现数据，数据的格式包含：数值型数据、字符型数据和逻辑数据，为保障数据分析的有效性，必须对数据进行规范化处理。为此，本文对字符型数据进行编码，使其转化为数值型数据，其中，对于famsize特征：LE3编码成0，GT3编码成1；Pstatus特征：T编码成0，A编码成1。对于逻辑型数据，通过编码使其转化成数值型数据，为此，对于特征activities，higher，Internet和romantic的属性值，TRUE编码成1，FALSE编码成0。

同时，本文对学生表现数据集进行异常值检测并清理。本文选择G3(最终成绩)作为数据标签，并查看其数据分布。从G3的数据分布可以看出，数据分布从0～20，可以看出大部分学生的成绩分布在8～15分，小部分的学生分布在0～7和16～20。其中，对于数据集中G1(第一阶段成绩)、G2(第二阶段成绩)、G3(第三阶段成绩)的关联性来看，对于G3为0 的学生而言，G1和G2很高，而G3为0，说明该学生G3成绩数据存在异常，为此，为保障分类的准确性，将数据集中G3为0的38条数据进行清除，至此，数据集共有357条。

1.4 一维数据集的K-means聚类

从G3的数据分布上可以看到数据集成绩分布在0～20，等级划分较为松散，在数据集样本量不大的情况下，不利于数据分类预测，为此，为保障数据标签划分的合理性，本文采用K-means聚类算法，将数据划分成两类，分别是warning和keeping两类标签，用0和1代替。

2 决策树预测模型的构建

针对学生表现分类，本文利用已有研究结果，考虑到方法适用性以及理论成熟性，在数据挖掘算法中选择了决策树分类方法[3]。

决策树算法包含有ID3，C4.5和 CART树，其中CART树又称为分类回归树，既可用于分类，也可用于回归。当数据集的因变量是离散值时，可以采用CART分类树进行拟合[4]。本文中，数据集特征均为离散型数据，且特征较多，适合使用CART树进行分类。

2.1 决策树建模流程

决策树建模过程是一个递归的过程，基本步骤如下：

(1)首先加载样本数据。

(2)根据样本特点，选择合适的特征选择标准。

(3)开始将所有记录看作一个节点。

(4)根据特征选择标准，遍历每个变量的每一种分割方式，找到最好的分割点。

(5)分割成两个节点N1和N2。

轮式机器人的线速度可通过编码器获得，设两轮轮距为L，编码器的线数为P（轮子转一圈编码器输出的脉冲数），轮径为D。通过左右编码器的脉冲频率fL和fR可以算得左右轮子的线速度为：

(6)对N1和N2分别继续执行(3)-(5)步，直到每个节点足够“纯”为止。

(7)生出决策树模型。

2.2 特征选择标准

决策树算法通过大量数据集样本训练，构建树形结构来描述分类规则。其中，树形结构是关键，需要确定树上的每一层的属性，前提是需要确定特征选择标准。

对于CART 决策树算法使用基尼指数来选择划分属性，基尼值代表了根据某一特征属性分类后的数据的不纯度。基尼值越小表示集合纯度越高，反之，集合越不纯[5]。

其中，数据集D中有K个类，k表示类别；pk表示样本属于第k个类别的概率。

对于特征A，将集合D划分成D1和D2，基尼指数G(D，A)表示经过特征A划分后集合D的不确定性，公式如下：

其中，∣D∣，∣D1∣，∣D2∣分别表示数据集D，D1，D2中样本数量。

3 实验结果与分析

CART模型在学生表现分类中的应用。具体过程，由于总样本量共357条，样本量不大，为提高训练模型的泛化能力，采用K折交叉验证法，其中k=10，选择其中285条数据作为训练集数据来进行模型拟合，利用剩下72条数据作为测试集来进行模型预测，验证模型准确率。

在建模方面，通过网格搜索找到最优参数，设定决策树模型关键参数为criterion="gini"，max_depth=3、min_samples_split=25，random_state=0。

通过CART算法对数据集进行决策树模型建立，如图1所示。其中，每一个内部结点特征取值为是和否，左分支是，右分支否。每个节点第一个属性表示分割节点条件，samples 表示这一层分类使用的样本数，class表示所属类别，value中的两个值分别表示标签为warning和keeping的样本数。

图1 决策树模型

根据CART模型可以得到影响学生表现的重要指标以及指标内容指向。从图1中可以看出，对学生表现影响比较大的因素分别是goout，absences，health以及Internet。从根节点右分支来看，当学生goout次数大于3.5，且学生健康指数大于2.5，学生旷课次数大于7次，可以明显地判定出学生表现会很差。即对于初中学生而言，如果出去次数过多，在身体允许情况下，经常旷课，会严重影响学生表现。因此，在今后学生管理中，对于学生家长，要适当约束学生外出次数，对学校管理要加强学生考勤工作，在身体允许情况下，保证出勤次数，以此来确保学生有足够时间投入学习，达到提高成绩的目的。

4 结语

本文采用决策树算法对学生表现数据集中的famrel，goout，health和absences等12个特征进行分析，建立了决策树CART模型。从决策树规则中可以看出，学生要积极锻炼身体保证身体健康，家庭方面要合理地限制学生外出次数，学校要严格执行考勤制度，确保学生在健康情况下，要应出勤尽出勤，以此来保障学生的投入学习，提高教学效果，保障教学质量。