基于多源数据的机器学习在地震预测中的研究进展
朱俊清 孙珂
中国地震局地震预测研究所,北京 100036
0 引言
地震是一种突发的、剧烈的地壳运动形式,是给人类社会带来人员伤亡、经济损失最严重的自然灾害之一。据相关数据统计,20世纪全球各地发生了多达1100多次破坏性地震,造成150多万人死亡(Yariyan et al,2020)。我国是地震多发国家,地震具有频度高、强度大、震源浅、分布广的特点,地震灾害给我国造成了严重的损失(夏朝旭等,2022)。
为减少地震对人类社会的危害,20世纪90年代全世界地震研究者就地震能否预测展开讨论。Geller等(1997)认为大量的物理条件决定着小地震能否演化成大地震,而不仅仅取决于断层,地震破裂高度敏感的非线性影响地震的可预测性;此外,即使已经发现了大量地震前兆,但没有定量的物理机制把前兆和地震联系起来,因此认为地震是不可预测的。Brehm等(1999)利用从断裂力学和裂纹拓展中推导出来的中期地震预测的失效时间方法,来定位和预测未来主震的大小和时间。无论是持地震不可预测观点或是持地震可预测观点的学者,均认可在当时科学认知和科技发展受限条件下,暂时不能实现地震的准确预测。
近年来,人工智能技术迅速发展,尤其是机器学习和深度学习在自然语言处理、计算机视觉、数据挖掘等具有多源海量复杂数据的领域取得蓬勃发展,在某些预测应用中获得了比传统方法明显优异的结果。很多地震工作者将基于数据特征和算法建模的人工智能方法运用到地震研究中,试图发现复杂地震数据与地震发生之间的联系,并尝试预测地震。研究算法从基于规则发展到浅层机器学习和深度学习,研究数据也基本包含了各类地震数据。
本文从机器学习背景、地震预测方法和评价指标等方面,回顾机器学习历史发展过程以及机器学习在地震预测应用中的常用流程,比较各算法模型的性能评价指标;并将数据按学科分类,讨论多源数据在基于机器学习的地震预测中的应用进展,在比较各算法表现的基础上,对机器学习在地震预测中应用的趋势发展进行总结和讨论。
1 研究背景
1.1 机器学习背景介绍
人工智能(Artificial Intelligence)是一门涉及计算机科学、逻辑学、信息学、哲学、生物学、心理学、语言学等多学科的交叉学科,在模式识别、机器学习、计算机视觉、自然语言处理、机器人学等应用领域获取了前所未有的成果(崔雍浩等,2019)。机器学习是人工智能核心,涉及概率论、统计学、算法复杂度理论、逼近论、凸分析等多学科,通过计算机技术模拟人类学习过程,并实现机器的自动识别(袁爱璟等,2021)。机器学习包括监督学习、无监督学习和半监督学习。监督分类分为分类和回归,现有的大多数地震预测算法均属于监督分类。无监督分为聚类和降维,聚类包括层次聚类、神经网络聚类等;降维包括主成分分析、线性判别分析等。深度学习是机器学习的重要组成部分,自2012年深度卷积神经网络在ImageNet大赛上获取了正确率超越第二名10%的优越成绩以来,深度学习进入高速发展时期。深度学习是一种基于深度神经网络算法模型技术,网络深度往往深达几十层,甚至上百层,如VGG网络有16层或者19层,GoogleNet有22层,ResNet具有从18层到152层等多个不同层数的具体模型,但是并不是层数越多性能越好,具体性能由数据、激活函数、模型参数等多个因素共同决定。人工智能技术自1943年诞生以来,发展历经坎坷,但总体上呈现上升趋势,自2012年至今处于快速发展时期。图1展示了自神经元诞生以来人工智能技术的主要发展历程。

注:该图据陈运泰(2009)、焦李成等(2016)、张荣等(2018)、包俊等(2020)、袁爱璟等(2021)研究中关于人工智能的历史发展综合绘制。
1.2 机器学习地震预测
机器学习地震预测方法涉及数据输入、数据预处理、算法选择、数据输出和评价指标等5个部分(图2)。数据输入的类型主要以各类地震观测数据为主,记录震前长时序的某个参数的持续变化。不同数据的载荷不同,记录的数据中会存在一定数量的无用值或空值,故需要对数据进行预处理,以满足模型处理的格式要求;算法选择面较广,包括基于规则的算法以及浅层神经网络和深层神经网络等不同类型的算法;数据的输出包括预测地震的发生时间、地点、震级和概率等,有些研究不会给出具体的输出,而是给出通过已发生地震验证的算法精确度;评价指标是评估算法模型好坏的关键,通过比较指标,对比不同模型的性能,从而选择基于某种数据的最佳模型,以达到最优预测(张荣等,2018)。

图2 机器学习地震预测流程(据Al Banna等(2020))
1.3 机器学习评价体系
建立良好的评价体系有利于评估机器学习地震预测的性能,有利于对比分析不同特征参数和不同模型算法的性能,从而有利于选择最优参数和模型。机器学习评价指标根据算法的不同,一般可以分为2种,一种为分类算法指标,另一种为回归算法指标。
1.3.1 分类算法评价指标
传统机器学习分类算法一般为二分类问题,即正例和反例,根据真实情况和预测结果的组合划分为真正例TP(true positive)、假正例FP(false positive)、真反例TN(true negative)和假反例FN(false negative)。在地震预测应用中,正例代表有地震,反例代表无地震。分类结果混淆矩阵如表1所示。

表1 分类结果混淆矩阵(据袁爱璟等(2021))
一般而言,混淆矩阵中做出正确预测的TP和TN数量多、且做出错误预测的FN和FP数量少的情况下,认为预测结果较好。但是简单的分类结果尚且不能完全表示模型的好坏,可以从混淆矩阵拓展出很多相关性的评价指标。表2为分类结果延伸出的8个评价指标。
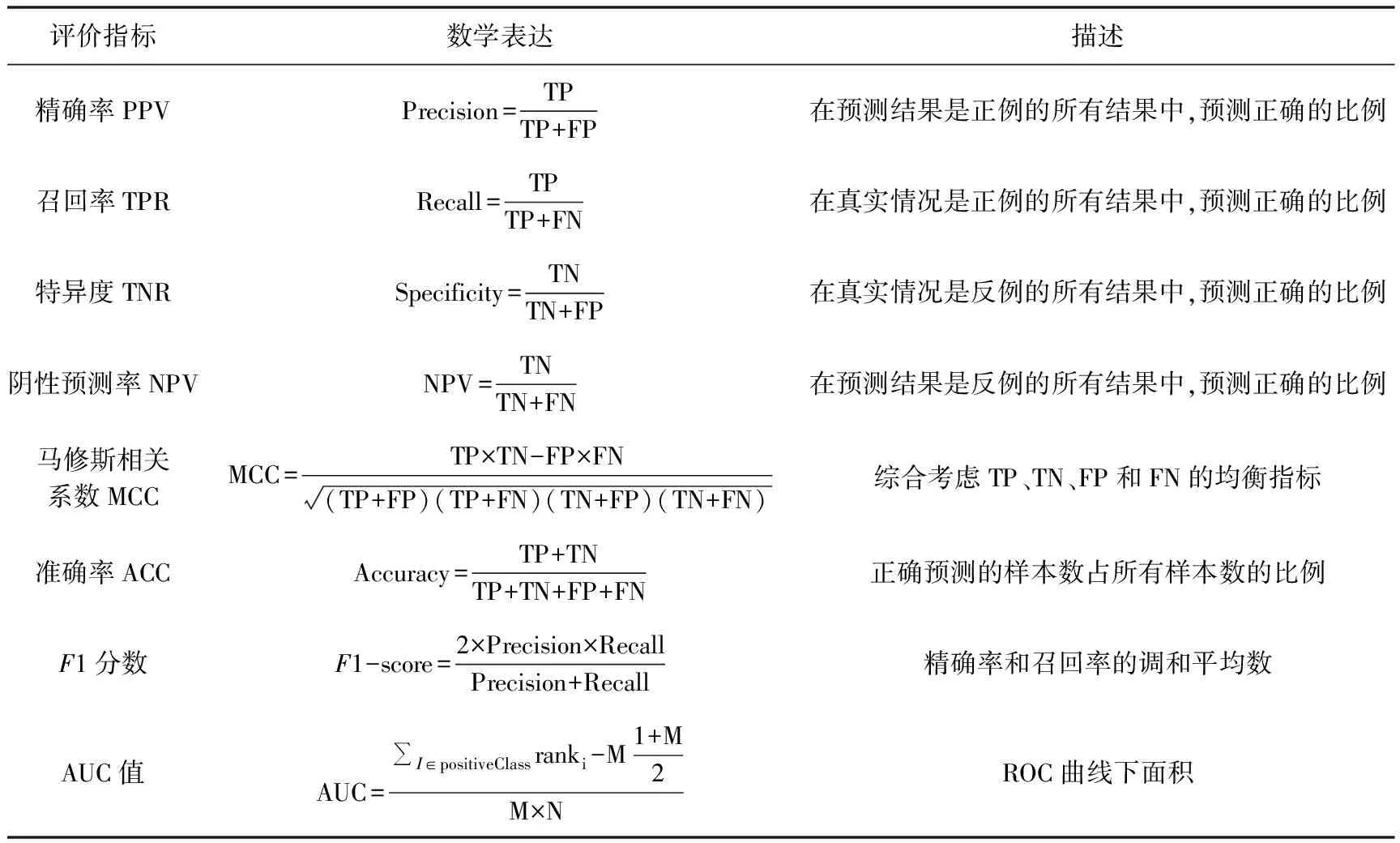
表2 分类算法评价指标(据Asencio-Cortés等(2017a)、袁爱璟等(2021))
AUC(area under curve)是受试者工作特征曲线(ROC曲线)下面积,除了表2中的计算方法外,还可以通过计算面积得到。由于ROC曲线能有效评价预测模型的性能,因此被广泛使用。一般而言,AUC值若为1,则为一个完美的分类器,AUC值为0.5则认为是随机猜测,模型预测结果没有具体价值,AUC值在0.5~1之间,越接近1,预测效果越好(袁爱璟等,2021)。另外,Asencio-Cortés等(2017a、2017b、2018)使用PPV、TPR、TNR和NPV的均值评价模型性能。
1.3.2 回归算法评价指标
在震级预测应用中,常运用回归算法将震级预测值和真实震级作回归分析,比较误差,回归值和预测值越接近,算法的预测性能越好。表3给出一些常用的回归算法评价指标。
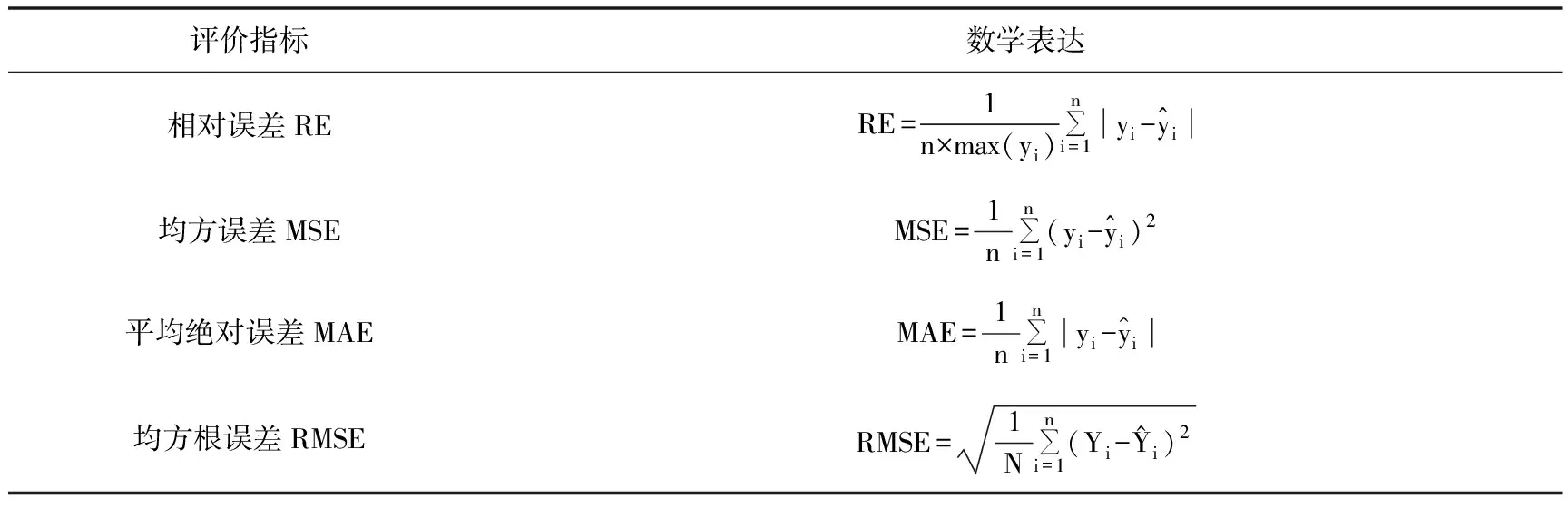
表3 回归算法评价指标(据Asencio-Cortés等(2018)、Salam等(2021))
2 多源数据在地震预测中的综合应用
2.1 地震学
2.1.1 地震目录数据
地震目录是按照时间顺序对地震参数进行收录和编目所形成的资料,是开展地震活动性研究的基础数据(王想等,2017)。地震目录通常包括发震时刻、震中位置、震源深度、震级等参数,而地震活动性研究的重要内容是分析这些参数在空间和时间维度上的分布特征(王想等,2016)。
Aslam等(2021b)利用统计聚类热点分析方法获取巴基斯坦北部地区地震活动热点区域(图3),分析表明兴都库什地区和2005年克什米尔地震发生的主边界逆冲断层所定位的中部地区为主要地震发生率较高地区,即地震活动热点地区;人工智能神经网络模型(ANN)仅使用震级信息作为训练特征对上述地区进行研究,模型训练精度达到74%,测试精度达69%,0.69虽然表现一般,但对于复杂的地区特征,仍是一个较不错的结果。

图3 Anselin局部莫兰指数聚类分析(a)和热点分析(b)(据Aslam等(2021b))
Jain等(2021)以目标地震震中为中心,根据不同半径值分割整个数据集,不同半径(100km、200km、500km、1000km、1500km、3000km和5000km)范围内地震的经纬度信息和震源深度信息作为特征参数,选用随机森林回归(RF)、多层感知器回归(MLP)和支持向量回归(SVR)对震级信息进行回归分析,获取均方根误差,在所有半径范围内MLP回归算法的RMSE值均最小,回归预测的震级和实际震级的误差最小。
人工智能神经网络在其他领域时间序列的预测上已取得广泛应用。Kaftan等(2017)为了验证不同神经网络在地震时间序列应用的性能,获取1975—2009年土耳其西部某地区震级大于等于3.0级地震,整理得到每月的地震频率,使用多个不同频率数输入多层感知器神经网络(MLPNN)、径向基函数神经网络(RBFNN)和自适应神经网络模糊推理系统(ANFIS),测试结果表明,RBFNN的RMSE值低于MLPNN和ANFIS的结果,在时间序列数据表现较好。Wang等(2020)在时间序列基础上加入空间信息,利用LSTM网络发现地震之间存在的时空相关性,将中国研究区分为9个区域,使用1966—2016年相邻地区地震数据,设置时间间隔为一个月,输入为某一子区域在该时间间隔内发生地震的次数,总的数据为一个600×9矩阵,总的预测精度为74.81%,在拥有多条断裂的某些子区域内组合的预测准确率可达88.57%。
2.1.2 地震活动性参数
Panakkat等(2007)和Adeli等(2009)根据古登堡-里希特逆幂律和地震震级特征分布,获得8个具有一定数学原理的地震活动性特征参数(表4),利用神经网络预测地震震级,在当时地震预测性能高度不确定的情况下,取得了较好的效果。

表4 地震活动性参数(据Asencio-Cortés等(2017b)、吴晶晶等(2019))
Asencio-Cortés等(2017a、2017b、2018)在这些地震活动性参数基础上进行改进,增加了其他特征参数,包括计算了一定地震间隔的b值增值、使用概率密度函数记录震级大于等于目标震级的概率和记录最近一周的最大震级等。Asencio-Cortés等(2017a)在对某些特定位置且空间分辨率较小的震例分析时,对东京200km范围内中大地震震级进行预测,ANN神经网络各评价指标均值均大于70%,结果优于其他测试算法。大数据技术的强大计算能力能够挖掘隐藏在杂乱数据中的有效信息,Asencio-Cortés等(2017b)在大数据技术加持下,基于云的大数据计算预测加利福尼亚地区未来7天内地震震级,首先使用4种算法单独训练,发现随机森林(RF)表现最好,其次将RF算法和其他3种算法进行集成学习,利用集成后的算法重新训练。不同算法集成在不同震级范围的平均绝对误差各不相同,不存在某种表现均优异的算法,但总体上相对误差接近10%,绝对误差接近0.5。
Asim等(2017b、2018)在对兴都库什地区震级大于等于5.5级地震进行预测时,使用8个地震活动性参数,验证了地震发生虽然是绝对非线性的,类似于随机事件,但可以根据发震区地球物理情况和极其复杂的机器学习模型对地震事件进行建模学习。此外,Asim等(2017a)对巴基斯坦北部地区地震进行研究时,根据信息增益情况剔除8个指标中的震级亏损和均方误差,选择其余6个指标作为神经网络的训练特征,在对预测模型进行McNemar’s统计测试后,比较各算法的显著性,前馈神经网络(Feed-Forward Neural Network)显著性为0.005且准确性为0.70,因此FFNN模型更适合巴基斯坦北部地区的地震预测。短临地震预报是减少人员伤亡和财产损失的关键所在,Asim等(2018)为了提高15天内对5.0级地震预测的准确性,将基于基因规划的GP算法和AdaBoost算法的集成算法与标准地震活动性参数相结合,并在兴都库什、智利和南加州地区进行实验,3个地区的地震预测精确度分别是78.7%、84.5%和86.6%,均取得比前人研究更好的结果。Asim等(2020)在分析塞浦路斯低级别地震时,更是创新性地选用总复发时间等多达60个地震特征预测未来5天、7天、10天和15天内发生地震震级,在震级阈值相同的情况下,较长时间阈值预测值MCC较好,随着震级阈值的增加,预测值MCC也随着降低。
除上述研究外,其他学者也基于地震活动性参数从算法创新和结合其他指标进行地震预测研究,其他地震指标作为地震活动性参数的补充,在一定程度上填补了地震活动性参数未能涉及到的物理机制,算法的优化和其他领域算法的跨领域应用对提升地震预测训练能力和测试精度上有很大帮助。吴晶晶等(2019)利用反向选择算法生成检测器,减少了对数据量较少的大地震的依赖性,对四川省历史地震进行训练,对其一个月内发生5.0级地震进行预测,结果明显好于神经网络和支持向量机;周天祥等(2019)和Zhou等(2020)将主要运用于计算机安全领域的树突状细胞算法DCA(Dendritic Cell Algorithm)应用到地震预测,在大多数数据集上的表现均优于其他算法;张研等(2020)将RVM(Relevance Vector Machine)预测算法与BP神经网络及SOM-BP神经网络算法进行比较,结果表明RVM算法优于其他2种算法;Salam等(2021)提出了2个混合机器学习地震预测模型,第一个为花授粉算法FPA(Flower pollination algorithm)和极限学习机ELM(Extreme learning machine)的混合模型FPA-ELM,第二个为FPA和最小二乘支持向量机LS-SVM的混合模型FPA-LS-SVM,混合了FPA算法的ELM和LS-SVM算法的精度均有所提高,在90%训练集和10%测试集的情况下,混合后ELM模型的RMSE为0.529,优于LS-SVM模型的0.537。Majhi等(2020)采用功能链接神经网络(Function Link Artificial Neural Network)对地震非线性数据建模,并结合最小二乘回归、飞蛾火焰优化算法(Moth-flame optimalization algorithm)、自适应梯度下降和LM反向传播算法,比较预测回归模型的均方根误差,在诸多结合方案中,基于FLANN的MFO算法的均方根误差最小(0.0565),预测效果较好。Rahmat等(2020)仅使用地震b值作为地震前兆指标,在极限学习机和深度学习方法中进行b值预测,2种方法在不同训练集下的平均成功率均达到85%,但深度学习表现相比极限学习机有1.61%的性能优势。Yousefzadeh等(2021)认为前人的地震预测研究更多侧重于时间参数,而不是空间参数,并且特征分析过程中会剔除一些相关性较强的变量,所以在地震活动性参数基础上,使用核密度估计和双变量莫兰指数计算的新参数断层密度进行地震预测研究,在传统机器学习和深度学习算法中,新参数均有效提高预测的准确性,后续会在更多深度神经框架中评估新参数对预测性能的影响。
2.2 大地测量学
Karimzadeh等(2019)将不同的机器学习算法(朴素贝叶斯、K近邻、支持向量机、随机森林)和滑动分布、相邻活动断层方向、库伦应力变化相结合,研究伊朗克曼沙7.3级地震后震级大于2.5的余震,利用70%的余震,基于二进制的方法预测所有余震的空间位置。研究区域滑动分布信息来源于InSAR技术,SAR数据在低噪声水平下识别和获取;库仑应力变化可根据滑动分布模型和摩擦系数以及斯肯普顿系数定义;实验区内共有HZF、MMF-1、MMF-2和MMF-3四条断层,实验区信息如图4所示。研究区域余震限制在100km×80km范围内,并且将地理坐标转换为二元网格地图,点的缓冲区约为1.5km,发生余震标记为1,非余震标记为0。由于变量较多,绘制基于不同断层和算法的ROC曲线有利于直观比较,实验结果表明,除K近邻算法外,其他算法在添加断层信息后能有效提高AUC值,RF算法对断层敏感。总的来说,KNN和RF算法表现要优于NB算法。

注:(a)为根据Sentinel-1和ALOS-2数据的联合反演分析得出的克尔曼沙7.3级地震的滑动分布图;(b)为根据弹性半空间中Sentinel-1和ALOS-2数据集的二次采样相位展开位移结果推导出的克尔曼沙7.3级地震的库仑应力变化图;(c)~(f)为相邻断层的欧氏距离图。
DeVries等(2018)的研究不需要事先假设断层方向,基于静态应力标准进行余震预测。利用超过13.1万对主震-余震训练数据和超过3万多对主震-余震测试数据,在深度学习网络下预测余震位置并对比经典库仑破裂应力变化预测结果,两者的ROC曲线表明,神经网络(测试数据集中所有滑动分布和网格单元的合并AUC值为0.849)的性能要明显优于经典库仑破裂应力准则(AUC值为0.583),在1999年中国台湾集集7.6级、1995年日本神户7.2级和2005年克什米尔7.6级地震的单一震例分析中,神经网络的AUC值均优于传统库仑破裂应力变化准则的AUC值。
然而,Mignan等(2019)对DeVries等(2018)的这一结果表示怀疑,其在实验中,使用较为简单的神经网络双参数逻辑回归,基于测量距离和主震平均滑移参数,也能获得与DNN模型相同的性能,即AUC=0.85,实验结果证明,复杂深度神经网络一般情况下不会影响模型的整体性能,但较难准确地解释物理推理过程。

2.3 地球化学
研究表明,跨断层土壤气体(氡气、二氧化碳、汞、氢气等)在地震发震期间非常活跃(王喜龙,2021),而在机器学习的方法上,对于氡气的研究较多。氡是一种放射性气体,化学性质稳定,能溶解于水和有机物,并且具有较强的扩散能力和迁移能力,在地震发生时的高温高压环境下,容易吸附在其他物质上,从而可以反映物质在地壳内部的迁移情况(史杨等,2017),震前氡浓度异常变化也已经是地震前兆热点研究对象之一。1978年1月14日本伊豆大岛7.0级地震前夕,观测到地下水浓度突然下降,随后并显著增加(Wakita et al,1980);1995年1月17日神户7.2级地震前1~2个月,观测到氡浓度比往常增加了约4倍,且于震前9天达到峰值,是初始观测的10倍多(Igarashi et al,1995);近年来,不少学者将机器学习的方法用于识别震前氡异常,取得的效果优于其他传统技术(Haider et al,2021;Tareen et al,2019)。
Sikder等(2009)使用前人研究报告中的数据集,包括155个地震活动,每次活动包括8个不同地点测量的氡浓度和7项气候环境特征参数,算法上选择粗糙集理论算法和决策树C4.5算法,进行对比分析,结果表明决策树算法的总体精度高达93.55%,高于粗糙集算法的88.39%。
2.4 地球电磁学
电离层是位于60km以上的高层大气区域,由于宇宙射线(主要是太阳辐射)的电离作用,大气处于部分电离或者完全电离的状态,通过现有数据研究,科学家们发现强震前后电离层参数会发生扰动(杨许铂,2015)。震前电离层扰动机制复杂,许多学者尝试利用机器学习方法去识别电磁扰动并尝试预测地震。
Xiong等(2020)利用机器学习技术识别震前电磁扰动,从DEMETER卫星数据中选择11个电场频带和6个磁场频带,为了验证机器学习技术的可靠性和鲁棒性,在已经选取的2005—2010年8760次大于等于5.0级地震的基础上,生成8760个人工非地震事件,训练算法包括常用的15种机器学习算法和深度神经网络,为了提高模型选择的置信度,利用贝叶斯优化进行超参数调整和五重交叉验证进行性能评估。实验表明,LightGBM算法在众多算法中表现最优,13个数据集训练下,AUC基本大于0.88,最高为0.986,识别震前电磁扰动最为准确。Xu等(2010)基于反向传播神经算法,利用DEMETER卫星获取的电子密度、电子温度、离子温度、氧离子密度、氢离子密度、氦离子密度以及地震带参数作为神经网络特征因子,其中地震带参数是根据每个震中距地震带的距离计算的,若距离小于60km则参数为1,否则为0。模型对2007年大于等于6.0级地震DEMETER数据训练后,在2008年的117个震区样本和106个非震区样本中进行测试,结果表明该方法对震区预测效果较好,准确率为81.2%,非震区则为57.5%。Ma等(2010)使用相同的神经网络,特征因子剔除了地震带信息,获取了测试震区83.9%的地震预测准确率。
Xiong等(2020)研究表明,强震震区附近震前存在电离层TEC异常扰动;Nahornyi等(2020)提出一种基于TEC变化趋势的预测模型,并且得到±5%的预测偏差,验证了TEC作为地震预测标志的可能性;Akhoondzadeh等(2013)利用遗传算法检测所罗门群岛8.0级地震所引起的TEC异常变化;Xiong等(2021b)提出一种新的拓展编码器-解码器长短时记忆拓展神经网络预测TEC。机器学习技术广泛应用于TEC异常检测,有助于基于TEC参数的地震预测的研究。Brum等(2019)利用NOAA提供的VTEC文件,开发具有多层感知器的神经网络并应用于墨西哥恰帕斯州8.2级地震,训练后的模型在测试数据集上能达到85.71%的准确性,通过对比震前VTEC时序变化和台站3个不同方向的地震波形图,发现ANN模型在震前3小时内给出异常预警。
Xiong等(2021a)使用多源、多参数卫星数据用于震前异常检测,特征参数包括地表温度、表层温度、地球表面大气温度、表面水蒸气质量混合比、总臭氧负荷、反演一氧化碳总柱量、反演甲烷总柱量、出射长波辐射通量(AIRS)、晴空出射长波辐射通量和出射长波辐射通量(NOAA)。通过确定最佳时间特征和空间特征,获得1234次6~7级地震和137次7级以上地震,并生成1371次人工地震事件,基于K均值算法和滑动时间窗方法2种不同方法生成特征,再根据是否包含余震信息,最终获取一个完整的数据集。此外在算法上提出一种新的基于反向提升修剪树(Inverse Boosting Pruning Trees)的地震预报框架(图5),IBPT在不同机器学习方法、不同特征比较、考虑余震效应、不同时间窗和空间窗以及不平衡数据集上均能最优的效果,最后基于该算法,生成全球范围内的地震预测可能性图。
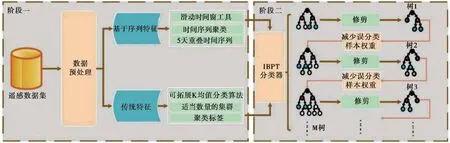
图5 IBPT框架流程图(据Xiong等(2021a))
2.5 地震地质学
在过去的几十年中,地震数据种类和数据量快速增加,为地震发生概率评估提供一定的条件。Jena等(2020a)首次尝试使用深度学习和GIS进行地震概率评估,研究使用的卷积神经网络使用9个特征指标,分别为断层接近度、断层密度、具有地震震动放大效应的岩性、坡度角、高程、震级密度、震中密度、距震中距离和地面峰值加速度密度。在GIS中生成每一指标的全区域专题图,获取地震点和随机创建的非地震点的像素值;设计CNN模型,用两类(0和1)地震预测;训练完成后将预测点的像素转换成格栅,从而生成GIS概率图。在整个印度次大陆的研究范围内,训练和测试数据集的整体准确度分别为96%和92%,取得较好的结果。
印度次大陆是一个面积较大的范围,空间分辨率较低,为研究某一特定较小范围区域内地震概率,Jena等(2021)又以印度东北部为研究区域,选用相同的特征指标,不同的是在卷积神经网络评估地震概率后,利用层次分析法、维恩交集理论和风险映射集成模型评估脆弱性,脆弱性评价指标主要为建筑物密度、远离建筑物距离、土地利用密度、远离土地利用距离、远离铁路距离和铁路密度,然后再结合区域的灾害应对能力(评价指标为医院数量和灾害预算),最终得到印度东北部的地震灾害风险图。
城市是人口、工业、经济产业密集区,若发生破坏性地震将会带来巨大的人员伤亡和财产损失,对城市抗震减灾和地震风险评估是地震工作者的首要任务。Jena等(2020b)利用人工神经网络和层次分析法,建立综合模型,研究分析印度尼西亚班达亚齐市地震风险。使用和上述研究相似的13个特征指标,通过在ANN中进行震例训练后,概率映射到GIS中生成各项指标的专题图,再利用MLP多层感知器绘制班达亚齐地震概率图(图6),实验获取的地震概率图准确率达到84%,层次分析法将脆弱性指标映射到GIS中生成专题图,并与地震概率图混合,生成地震风险图,通过分析研读风险图,发现班达亚齐市的地震中高风险主要分布在该市的中部和东南部地区,这些研究结果对未来抗震减灾和政府部门的政策制定有一定帮助。

图6 地震发生概率图(据Jena等(2020b))
3 总结与讨论
机器学习在其他预测领域取得的一定成果让学者们开始利用机器学习方法研究地震预测,在本文整理的近5年来30多篇地震预测应用文献中,基于地震学的地震目录和地震活动性指标数据的地震预测研究热度最高。而其他数据因为数据量、数据特征相关性和预测效能等影响,研究热度较低。现阶段基于机器学习的地震预测并没有最优算法,不同的研究侧重的算法不同,暂不能统计不同算法的研究热度。
地震预测效能是基于机器学习地震预测研究的重点关注内容之一,现阶段以地震活动性参数为数据并基于复杂算法模型进行地震预测已经达到瓶颈,预测精度较难提升,而基于震源数据以及延伸出来的地震发生频率、间隔时间等数据的地震预测仍处于发展阶段,研究成果较少,尚不能总结预测性能;基于库仑应力机器学习方法将余震预测归纳为平面或空间上,现有研究中不同特征参数和不同算法组合的AUC值基本处于0.75~0.85的范围内,少数AUC值能超过0.9,整体预测性能较好;基于氡气数据机器学习方法预测地震的研究较少,由于氡气特别受外部环境影响,包括不同深度的土壤温度、降雨和大气压力等因素,故整体研究成果不理想;现有的基于地球电磁地震预测研究准确率超过80%,但由于数据量的限制,参考价值有限,然而基于机器学习方法的空间电磁异常识别整体效果能达到较高水平,提高异常信号的识别能力有利于提升地震预测特征参数的准确性;基于地震地质数据的地震概率预测对于中长期地震震害防御有所帮助。图7整理了现有研究中出现较多的算法有效指标,由于某些算法的训练指标和结果表现形式不一样,无法通过某一特定指标进行直接比较。
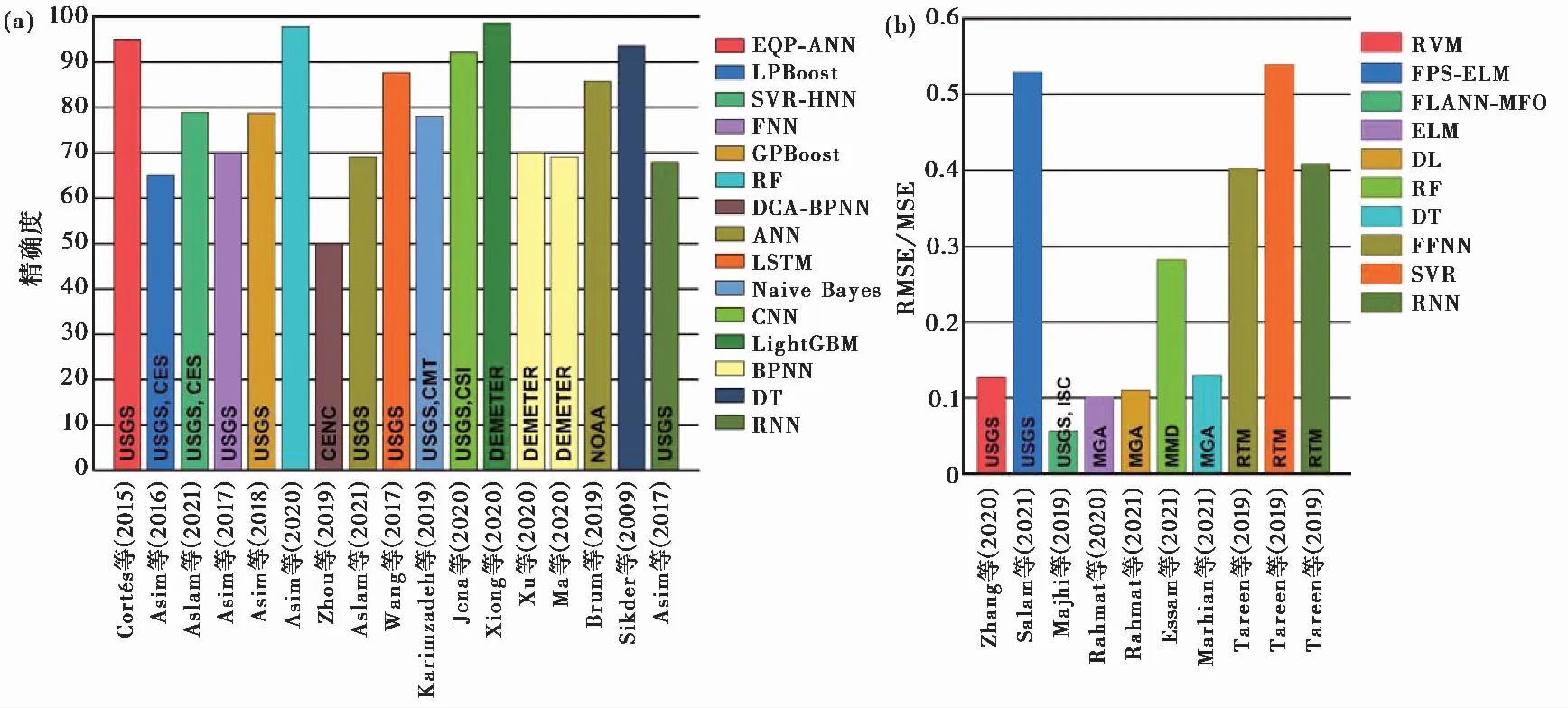
注:基于分类算法和回归算法在地震预测上的表现主要以精确度(a)和均方根误差/均方误差(RMSE/MSE)(b)表示;其中,地震预测精度普遍高于65%,DCA-BPNN表现最差,约50%,LightGBM算法精度最高;回归误差表现差异较大,误差值在0.1附近和大于0.4的最多,中间表现较少;从数据来源上分析,USGS数据使用最广泛,其他各国地震研究机构的数据也会偶尔被使用。
基于不同学科的地震研究迅速发展,产生了海量数据,但有效用于机器学习地震预测的只占地震数据的小部分,仍有大量的观测数据待挖掘;不同数据若能跨学科使用,将有利于在不同维度上接近地震物理机制;另一方面,具有不同空间特征或时间特征的数据,若可以相互匹配融合,能够克服单一数据源有限性问题,例如空间范围广、时效性长的空间电磁数据与定点定位、时效性短的地电磁数据的融合使用。特征参数的选择需要尽可能还原地震发震的物理机制,另外值得注意的是新兴特征参数的效能也需深入研究,例如地球化学中的同位素;算法模型对预测结果影响较大,例如DeVries等(2018)用多达13000多个参数进行余震预测,而相同震例条件下,Mignan(2019)仅用2~3个参数就获得了类似的结果。地震预测研究算法繁多,很难找到一个通用的最优算法,更多的目的是基于某一地区寻找可能适合该地区的最优算法,另外其他领域的一些深度学习优秀算法性能往往优于传统机器算法,增加这些算法在地震预测的使用是提高地震预测效果的一种途径。
一般意义上的地震预测需要预测出地震发生的大概时间、地点和震级,而现有的大部分机器学习地震预测并不会提供准确的时间、地点和震级,而是通过比较不同预测算法的效能,获取在某一区域或基于某一数据集表现最好的算法;基于回归算法地震预测给出的预测震级,是基于某一区域内震例的震级,预测的范围相对较广,很难定位到某个特定地点。
总体来说,现阶段基于机器学习地震预测很难给出较为准确的地震时间、地点和震级,主要原因是神经网络有限的特征参数很难完全体现地震孕育的复杂因素,以及神经网络内部的运算过程难以完全匹配地震的复杂发震机制。基于机器学习地震预测的学术研究到地震预测的真正应用之间还有很长一段路程。

